- Research
- Open access
- Published:
An inertial-type algorithm for approximation of solutions of Hammerstein integral inclusions in Hilbert spaces
Fixed Point Theory and Algorithms for Sciences and Engineering volume 2021, Article number: 8 (2021)
Abstract
Let H be a real Hilbert space. Let \(F:H\rightarrow 2^{H}\) and \(K:H\rightarrow 2^{H}\) be two maximal monotone and bounded operators. Suppose the Hammerstein inclusion \(0\in u+KFu\) has a solution. We construct an inertial-type algorithm and show its strong convergence to a solution of the inclusion. As far as we know, this is the first inertial-type algorithm for Hammerstein inclusions in Hilbert spaces. We also give numerical examples to compare the new algorithm with some existing ones in the literature.
1 Introduction
Let Ω be a measurable bounded subset of \({\mathbb{R}}^{n}\). A nonlinear integral equation of Hammerstein type is of the form
where dy is a σ-finite measure. The function \(k:\Omega \times \Omega \rightarrow \mathbb{R}\) is the kernel of the equation, and \(f:\Omega \times \mathbb{R} \rightarrow \mathbb{R}\) is a measurable real-valued function. The function w and the unknown function u lie in a suitable Banach space of measurable real-valued functions, say, \(\mathcal{F}(\Omega, \mathbb{R})\). If we define the operators \(F:\mathcal{F}(\Omega, \mathbb{R})\rightarrow \mathcal{F}(\Omega, \mathbb{R})\) and \(K:\mathcal{F}(\Omega, \mathbb{R})\rightarrow \mathcal{F}(\Omega, \mathbb{R})\) by
then (1.1) can be easily written as the abstract Hammerstein equation
where, without loss of generality, we have taken w to be the zero map in \(\mathcal{F}(\Omega, \mathbb{R})\). Interest in Hammerstein equations stems mainly from their applications in various fields. For instance, (1.1) can be used to describe the final state of a spatially distributed population (see, e.g., [30] and [42]). Consider also the following nonlinear boundary value problem:
where Ω is a smooth subset of \({\mathbb{R}}^{n}\). Define the operator \(K:\mathcal{F}(\Omega, \mathbb{R})\rightarrow \mathcal{F}(\Omega, \mathbb{R})\) by \(Kg=u\), where u is the unique solution of the corresponding linear boundary value problem
Then (1.4) can be written in the form (1.3), where F is as defined in (1.2). Other areas of application of Hammerstein integral equations include differential equations (see, e.g., Pascali [38]), optimal control system, automation and network theory, and many other areas (see, e.g., Doležal [31]). If the operator F in (1.3) is multivalued and defined by
then (1.3) becomes the Hammerstein inclusion

Hammerstein inclusions are closely related to nonsmooth calculus of variations. For instance, consider the energy functional given by
where h denotes the kinetic energy of the system, and f is the potential energy generator of the superposition operator. In general, the functional J is not differentiable in the classical sense. However, it admits generalized gradient or subgradient in the sense of, for instance, Clarke’s generalized gradient (see, e.g., [29]). Consequently, the problem of minimizing the energy functional J leads to the Euler–Lagrange inclusion

where L is a linear operator, and ∂F is the generalized Clarke gradient. Equation (1.8), in turn, is equivalent to (1.6) defined on a suitable Banach space of measurable real-valued functions. Let H be a Hilbert space. A map \(A:H\rightarrow 2^{H}\) is called monotone if for all  ,
,

Several existence results have been proved for (1.3) when the operators F and K are monotone. (See, e.g., Brézis and Browder [4–6], Browder [7, 8, 10, 11], Browder and De Figueiredo [11, 12], Chepanovich [14], Appel et al. [3], and Cardinali and Papageorgiou [13]). In general, there is no closed-form solution for Hammerstein integral equations. Therefore developing algorithms for approximating such solutions is of great interest. Let \(A:H \rightarrow H\) be a nonlinear operator. Then A is said to be angle bounded with angle  if
if

for all  . For \(y=z\), inequality (1.10) implies the monotonicity of A. A monotone linear operator \(A:H\to H\) is said to be angle bounded with angle
. For \(y=z\), inequality (1.10) implies the monotonicity of A. A monotone linear operator \(A:H\to H\) is said to be angle bounded with angle  if
if

for all  . Brézis and Browder [5] proved the following theorem for the approximation of solutions of Hammerstein equations with angle-bounded operators using a suitably defined Galerkin method.
. Brézis and Browder [5] proved the following theorem for the approximation of solutions of Hammerstein equations with angle-bounded operators using a suitably defined Galerkin method.
Theorem 1.1
(Brézis and Browder [5])
Let H be a separable Hilbert space, and let C be a closed subspace of H. Let \(K:H \to C\) be a bounded continuous monotone operator, and let \(F:C\to H\) be an angle-bounded and weakly compact mapping. For a given  , consider the Hammerstein equation
, consider the Hammerstein equation
and its nth Galerkin approximation given by
where \(K_{n}=P_{n}^{*}KP_{n}:H\to C\) and \(F_{n}=P_{n}FP_{n}^{*}:C_{n} \to H\), with the symbols having their usual meanings (see, e.g., Pascali [38, Chap., p. 202]. Then, for each  , the Galerkin approximation (1.13) admits a unique solution \(u_{n}\) in \(C_{n}\), and \(\{u_{n}\}\) converges strongly in H to the unique solution
, the Galerkin approximation (1.13) admits a unique solution \(u_{n}\) in \(C_{n}\), and \(\{u_{n}\}\) converges strongly in H to the unique solution  of equation (1.12).
of equation (1.12).
Attempts have been made to develop iterative algorithms for approximating solutions of (1.3) (see, e.g., Mann [21, 35] and the references therein). However, most of these results require the inverse of the operator K not only to exist but also to be strongly monotone. These requirements do not only limit the class of operators involved but are also not convenient for implementation. The first satisfactory result for approximating solution of Hammerstein equation was given by Chidume and Zegeye [26–28]. They considered the product space \(E=H\times H\) and defined the auxiliary operator \(T:E\rightarrow E\) by

We can easily see that \(u^{*}\) solves (1.3) if and only if \(T[u^{*},v^{*}]=0\) with \(v^{*}=Fu^{*}\). The auxiliary operator T gave an insight on how to develop a coupled algorithm for computing solutions of (1.3). The same authors (see [28]) defined the following coupled algorithm: for  , define the sequences \(\{u_{n}\}\) and \(\{v_{n}\}\) recursively by
, define the sequences \(\{u_{n}\}\) and \(\{v_{n}\}\) recursively by


where \(\{\alpha _{n}\}\) is a sequence in \((0,1)\) satisfying appropriate conditions. Many strong convergence results have been proved in Banach spaces by many authors using the coupled algorithm. (See, e.g., Chidume and Djitte [17–19], Chidume and Ofeodu [20], Chidume and Shehu [23], Chidume and Osilike [22], and Chidume and Bello [15].) Recently, Minjibir and Muhammad [36] proved a strong convergence result for Hammerstein inclusion under the setting of Hilbert spaces. They proved the following theorem with the sequences \(\{\alpha _{n}\}, \{\theta _{n}\}\subset (0,1)\) satisfying some appropriate conditions.
Theorem 1.2
(Minjibir and Mohammad [36])
Let H be a real Hilbert space, and let \(F,K:H\rightarrow CB(H)\) be maps with \(D(F)=D(K) = H\) such that the following conditions hold:
-
(i)
F is monotone, continuous (relative to h), and bounded;
-
(ii)
K is monotone, continuous (relative to h), and bounded.
Let \(\{u_{n}\}\) and \(\{v_{n}\}\) be sequences generated iteratively from arbitrary  by
by

Suppose that the inclusion  has a solution in H. Then there exists a real constant
has a solution in H. Then there exists a real constant  such that if
such that if  for some
for some  , and then the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of
, and then the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of  .
.
The need to speed up the convergence of iterative algorithms has always been of great interest. One of the recent methods of speeding up the convergence is via addition of inertial terms to algorithms. The use of the term “inertial” can be traced back, at least, to Poljak [39], where he considered the following second-order system of differential equations:

in the context of optimization. In two-dimensional case, system (1.18) describes, roughly, the motion of a heavy ball that rolls under its own inertial over the graph of f until it is impeded by friction. For results concerning inertial algorithms, see, for instance, Moudafi [37], Alvarez [2], and Maingé and Merabet [32]. In this paper, we introduce an inertial algorithm for approximating solution of Hammerstein inclusion in Hilbert spaces. As far as we know, this is the first inertial algorithm involving Hammerstein inclusions. Our algorithm converges much faster than the existing noninertial algorithms for Hammerstein inclusions. We give numerical examples to support this claim. Moreover, in our theorem, we make no assumption of continuity of the operators.
2 Preliminaries
In this section, we present some definitions and lemmas used in the proof of the main theorem. We further assume that H is a real Hilbert space and \(E=H\times H \) is the Cartesian product of H. We define the norm \(\Vert \cdot \Vert _{E}\) on E by

Let W be any nonempty subset of H, and let  be fixed. Then the distance between x and W is given as
be fixed. Then the distance between x and W is given as  .
.
Definition 2.1
Let \(\operatorname*{CB}(H) \) denote the set of closed bounded subsets of H. Then the Hausdorff distance between two nonempty closed bounded subsets V and W of H is given as

It is well known that \(\mathcal{D} \) is a metric on \(\operatorname*{CB}(H) \). A multivalued mapping \(T: D(T)\subset H\longrightarrow \operatorname*{CB}(H) \) with domain  and range
and range  is monotone if
is monotone if

where the function \(\langle \cdot,\cdot \rangle _{H}\) is the inner product on H. A monotone map T is maximal monotone if its graph  is not properly contained in the graph of any other monotone map. It is well known that if T is maximal monotone, then the range \(R(I+\lambda T)=H \) for
is not properly contained in the graph of any other monotone map. It is well known that if T is maximal monotone, then the range \(R(I+\lambda T)=H \) for  . For
. For  , the resolvent operator is given by \(J_{\lambda }=(I+\lambda T)^{-1}\), where I is the identity map on H. The operator \(J_{\lambda }\) is always single-valued. (See, e.g., Browder [9, 33] for more detail.) The following inequality, which characterizes the monotone maps in Hilbert spaces, was given by Kato in [34]:
, the resolvent operator is given by \(J_{\lambda }=(I+\lambda T)^{-1}\), where I is the identity map on H. The operator \(J_{\lambda }\) is always single-valued. (See, e.g., Browder [9, 33] for more detail.) The following inequality, which characterizes the monotone maps in Hilbert spaces, was given by Kato in [34]:

for all  , and
, and  if and only if T is monotone. In what follows, we present the lemmas used in the proof of the main theorem.
if and only if T is monotone. In what follows, we present the lemmas used in the proof of the main theorem.
Lemma 2.2
(Xu [43])
Let \(\{a_{n}\}\) be a sequence of nonnegative real numbers satisfying

where (i) \(\{\alpha _{n}\}\subset (0,1), \sum \alpha _{n}=\infty \); (ii)  ; and (iii)
; and (iii)  . Then \(a_{n}\to 0 \) as \(n\to \infty \).
. Then \(a_{n}\to 0 \) as \(n\to \infty \).
Lemma 2.3
(Reich [40])
Let H be a real Hilbert space, and let \(A:D(A)\subset H\longrightarrow 2^{H} \) be maximal monotone. If  , then for each
, then for each  , the strong limit \(\lim_{t\rightarrow \infty }J_{t}x\) exists and belongs to \(A^{-1}0\), that is,
, the strong limit \(\lim_{t\rightarrow \infty }J_{t}x\) exists and belongs to \(A^{-1}0\), that is,  .
.
Lemma 2.4
Let H be a real Hilbert space, and let \(F:H\rightarrow CB(H),K: H\rightarrow CB(H)\) be two maximal monotone and bounded multivalued maps. Then \(T:E\rightarrow CB(E)\) defined by

is also maximal monotone and bounded.
Proof
The boundedness of T follows from the boundedness of F and K. Likewise, the maximal monotonicity of T follows from that of F and K (see Alber and Ryazantseva [1, p. 280]). □
3 Main theorem
Theorem 3.1
Let H be a real Hilbert space, and let \(F, K:H\rightarrow CB(H)\) be maximal monotone and bounded maps. For arbitrary  , define the sequences \(\{h_{n}\}\), \(\{p_{n}\}\), \(\{u_{n}\}\), and \(\{v_{n}\}\) by
, define the sequences \(\{h_{n}\}\), \(\{p_{n}\}\), \(\{u_{n}\}\), and \(\{v_{n}\}\) by

where \(\{\theta _{n}\}\) and \(\{\lambda _{n}\}\) are sequences in \((0,1)\), and \(\{c_{n}\}\) is a sequence in \([0,1)\) satisfying the following conditions:

Suppose that the inclusion  has a solution in H. Then there exists a real constant \(\gamma _{0} \) such that
has a solution in H. Then there exists a real constant \(\gamma _{0} \) such that  for all
for all  , for some
, for some  , and the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of
, and the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of  .
.
Proof
Consider the inner product on \(E=H\times H \) defined by

The norm induced by this inner product is given by (2.1). We define two sequences \(\{w_{n}\}\) and \(\{r_{n}\}\) in E by \(w_{n}:=(u_{n},v_{n})\) and \(r_{n}:=(h_{n},p_{n})\) for  . Let
. Let  be a solution of the inclusion
be a solution of the inclusion  with
with  \(Fu^{*}\) such that
\(Fu^{*}\) such that  . Now set \(w^{*}= (u^{*},v^{*} )\). To show that \(\{u_{n}\} \) and \(\{v_{n}\} \) converge strongly to \(u^{*} \) and \(v^{*}\), respectively, it suffices to show that \(\{w_{n}\}\) converges strongly to \(w^{*}\) in E. For any
. Now set \(w^{*}= (u^{*},v^{*} )\). To show that \(\{u_{n}\} \) and \(\{v_{n}\} \) converge strongly to \(u^{*} \) and \(v^{*}\), respectively, it suffices to show that \(\{w_{n}\}\) converges strongly to \(w^{*}\) in E. For any  and
and  , we define the closed ball in E with center w and radius t as
, we define the closed ball in E with center w and radius t as  . Let
. Let  be such that
be such that

where \(n_{0}\) is as defined in the theorem. Let

and \(M:=M_{1}+M_{2}\). By the boundedness of F and K, \(M_{1},M_{2}\), and M are all finite. The first step is showing that \(\{w_{n}\}\) is bounded, and then \(\{u_{n}\}\) and \(\{v_{n}\}\) will be necessarily bounded. By construction,  ,
,  . We now show that
. We now show that  for all
for all  . To do this, we proceed by induction. Supposing that
. To do this, we proceed by induction. Supposing that  up to some
up to some  , we show that
, we show that  . Using (2.1), we have
. Using (2.1), we have
Now
Since  , and F is monotone, we get that
, and F is monotone, we get that

Also,

Substituting (3.4) and (3.5) into (3.3), we obtain

Similarly,
where

Applying inequality (3.8) in (3.7), we have

Since K is monotone,  , and
, and  , we have
, we have

Using inequality (3.10) in (3.9), we get

Adding (3.6) and (3.11), we obtain

Observe that

Substituting (3.13) into (3.12), we see that

Furthermore, we have the following estimate:

Now taking \(\gamma _{0}=\frac{r^{2}}{4M}\) and using the assumption that  , by (3.15) we have that
, by (3.15) we have that

Thus \(\{w_{n}\}\) is bounded, which implies that \(\{u_{n}\}\) and \(\{v_{n}\}\) are bounded.
The next step is showing that there exists a sequence  , such that
, such that

\(x_{n}\rightarrow x^{*}\), \(y_{n}\rightarrow y^{*}\) with  , and
, and  . By Lemma 2.4 the map T defined in (1.14) is maximal monotone. Moreover, since \(\theta _{n}\rightarrow 0\), by Lemma 2.3 we get that
. By Lemma 2.4 the map T defined in (1.14) is maximal monotone. Moreover, since \(\theta _{n}\rightarrow 0\), by Lemma 2.3 we get that

Setting \((x_{n},y_{n}):= ( I+\frac{1}{\theta _{n}}T ) ^{-1}(0,0)\) for  , we have
, we have

Thus we have
for some  and
and  . This implies that
. This implies that

Consequently,

Using (3.17), we have  . However, we have that
. However, we have that

Thus \(x_{n}\rightarrow x^{*}\) and \(y_{n}\rightarrow y^{*}\) with  , and
, and  .
.
The final step is showing that \(w_{n}\rightarrow (u^{*}, v^{*})\), where  and
and  . Hence it suffices to show that \(w_{n+1}-z_{n}\rightarrow 0\) as \(n\rightarrow \infty \). Now
. Hence it suffices to show that \(w_{n+1}-z_{n}\rightarrow 0\) as \(n\rightarrow \infty \). Now
Since, by (3.18), \(\theta _{n}x_{n}=y_{n}-\hat{x}_{n}\), we observe that
for  and some
and some  , so that
, so that
Using the monotonicity and boundedness of F and employing the boundedness of the sequences \(\{u_{n}\}\) and \(\{v_{n}\}\), we get that there exists  such that
such that

From (3.18) we get that \(\theta _{n}y_{n}=-(x_{n}+\hat{y}_{n})\). Applying similar arguments, we obtain

for some constant  . Consequently, adding (3.19) and (3.20), we have
. Consequently, adding (3.19) and (3.20), we have

where \(M_{o}:=M_{3}+M_{4}\). Using the monotonicity of T and the Kato inequality (2.2), we have

where  , and
, and  . Using (3.18), we have that
. Using (3.18), we have that

and

Substituting (3.23) and (3.24) into (3.22), we have

From (3.21) we have

Using inequality (3.25) in (3.26), we have that

Thus by the boundedness of \(\{w_{n}\}\), \(\{z_{n}\}\), and \(\lbrace ((\theta _{n-1}-\theta _{n})/\theta _{n} ) \rbrace \) there exist  such that
such that

where \(L=\max \{\mathrm{C},M_{o}\}\). By Lemma 2.2 it follows that \(w_{n+1}-z_{n}\rightarrow 0\). This implies that \(u_{n}\rightarrow u^{*}\) and \(v_{n}\rightarrow v^{*}\), where \(u^{*}=x^{*}\) and \(v^{*}=y^{*}\). This completes the proof. □
Corollary 3.2
Let H be a real Hilbert space, and let \(F:H\rightarrow CB(H), K:H\rightarrow H\) be maximal monotone and bounded maps. For arbitrary  , define the sequences \(\{h_{n}\}\), \(\{p_{n}\}\), \(\{u_{n}\}\), and \(\{v_{n}\}\) by
, define the sequences \(\{h_{n}\}\), \(\{p_{n}\}\), \(\{u_{n}\}\), and \(\{v_{n}\}\) by

where \(\{\theta _{n}\}\) and \(\{\lambda _{n}\}\) are sequences in \((0,1)\), and \(\{c_{n}\}\) is a sequence in \([0,1)\) satisfying the conditions of Theorem 3.1. Suppose that the inclusion  has a solution in H. Then there exists a real constant \(\gamma _{0} \) such that
has a solution in H. Then there exists a real constant \(\gamma _{0} \) such that  for all
for all  , for some
, for some  , and the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of
, and the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of  .
.
Proof
It follows from the proof of Theorem 3.1 when K is single-valued. □
Corollary 3.3
Let H be a real Hilbert space, and let \(F,K:H\rightarrow H\) be maximal monotone and bounded maps. For arbitrary  , define the sequences \(\{h_{n}\}\), \(\{p_{n}\}\), \(\{u_{n}\}\), and \(\{v_{n}\}\) by
, define the sequences \(\{h_{n}\}\), \(\{p_{n}\}\), \(\{u_{n}\}\), and \(\{v_{n}\}\) by

where \(\{\theta _{n}\},\{\lambda _{n}\}\), and \(\{c_{n}\}\) are sequences in \((0,1)\) satisfying the conditions of Theorem 3.1. Suppose that the inclusion  has a solution in H. Then there exists a real constant \(\gamma _{0} \) such that
has a solution in H. Then there exists a real constant \(\gamma _{0} \) such that  for all
for all  , for some
, for some  , and the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of
, and the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of  .
.
Proof
It follows from the proof of Theorem 3.1 when F and K are single-valued. □
Definition 3.4
(Hemicontinuity)
An operator \(A:H\longrightarrow H \) is said to be hemicontinuous at a point \(x_{0}\) if for all \(x\in H\), \(A(x_{0}+t_{n}x)\rightharpoonup A(x_{0})\) as \(t_{n}\to 0^{+}\).
Theorem 3.5
([1, p. 29])
Let X be a reflexive Banach space, and let \(X^{*} \) be its dual space. Then every monotone hemicontinuous operator \(A:X\longrightarrow X^{*} \) is maximal monotone.
Corollary 3.6
Let H be a real Hilbert space, and let \(F,K:H\rightarrow H\) be hemicontinuous, monotone, and bounded maps. For arbitrary  , define the sequences \(\{h_{n}\}\), \(\{p_{n}\}\), \(\{u_{n}\}\), and \(\{v_{n}\}\) by
, define the sequences \(\{h_{n}\}\), \(\{p_{n}\}\), \(\{u_{n}\}\), and \(\{v_{n}\}\) by

where \(\{\theta _{n}\}\) and \(\{\lambda _{n}\}\) are sequences in \((0,1)\), and \(\{c_{n}\}\) is a sequence in \([0,1)\) satisfying the conditions of Theorem 3.1. Suppose that the inclusion  has a solution in H. Then there exists a real constant \(\gamma _{0} \) such that
has a solution in H. Then there exists a real constant \(\gamma _{0} \) such that  for all
for all  , for some
, for some  , and the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of
, and the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of  .
.
Proof
The maps F and K are maximal monotone by Theorem 3.5. The rest of the proof follows from Corollary 3.3. □
Remark 1
Note that if \(0< b< a\) and \(a+b<1\), then for each natural number n, \(\lambda _{n}=(n+1)^{-a}\) and \(\theta _{n}=(n+1)^{-b}\) satisfy the hypotheses of Theorem 3.1 (see [16]).
4 Algorithms for comparison
Mainly for numerical comparison, we present the following algorithms.
Theorem 4.1
(Chidume and Shehu (CS12) [24])
Let H be a real Hilbert space, and let \(F,K:H\rightarrow H\) be bounded, continuous, and monotone mappings. Let \(\{u_{n}\}\) and \(\{v_{n}\}\) be sequences defined iteratively from arbitrary  by
by

where \(\{\beta _{n}\}_{n}^{\infty } \) is a real sequence in \((0,1) \) such that \(\sum_{n=0}^{\infty }\beta _{n}^{2}<\infty \) and \(\sum_{n=0}^{\infty }\beta _{n}=\infty \). Then the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of \(u + KFu=0\).
Theorem 4.2
(Chidume and Shehu (CS13) [25])
For \(q>1\), let E be a q-uniformly smooth real Banach space. For each \(i=1,2,\ldots,m\), let \(F_{i},K_{i}:E\rightarrow E\) be bounded and accretive mappings. Let \(\{u_{n}\}\) and \(\{v_{i,n}\}_{n=1}^{\infty }, i=1,2,\ldots,m\), be sequences defined iteratively from arbitrary  by
by

where \(\{\lambda _{n}\}_{n}^{\infty } \), \(\{\alpha _{n}\}_{n}^{\infty } \), \(\{\theta _{n}\}_{n}^{\infty } \) are real sequences in \((0,1) \) such that \(\lambda _{n}=o(\theta _{n}), \alpha _{n}=o(\theta _{n})\), and \(\sum_{n=0}^{\infty }\lambda _{n}\theta _{n}=\infty \). Then the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\), a solution of \(u + \sum_{i=1}^{m}K_{i}F_{i}u=0\).
Theorem 4.3
(Shehu (S14) [41])
Let H be a real Hilbert space, and let \(F:H\rightarrow H\) be a bounded, coercive, and maximal monotone mapping. Let \(F:H\rightarrow H\) be a bounded and maximal monotone mapping. Suppose that both maps satisfy the range condition. Let \(\{u_{n}\}\) and \(\{v_{n}\}\) be sequences defined iteratively from arbitrary  by
by

where \(\{\beta _{n}\}_{n}^{\infty } \) is a real sequence in \((0,1) \) such that \(\lim_{n\to \infty }\beta _{n}=0\), \(\sum_{n=0}^{\infty }\beta _{n}^{2}<\infty \), and \(\sum_{n=0}^{\infty }\beta _{n}=\infty \). Suppose that \(u^{*}\) is a solution of \(u + KFu=0\). Then the sequence \(\{u_{n}\}\) converges strongly to \(u^{*}\).
5 Numerical examples
In this section, we present some numerical examples illustrating the advantages of the present algorithm (3.1) over MM (1.17), CS12 (4.1), CS13 (4.2), and S14 (4.3). We construct these examples on  , \(\ell _{2}(\mathbb{R})\), and \(\mathcal{L}^{2}_{\mathbb{R}}(\Omega )\), where Ω is a closed bounded interval of \(\mathbb{R}\). Numerical experiments were carried out on MATLAB R2013a and R2020 versions. All programs were run on PCs with Intel(R) Core(TM)2 Duo CPU and 3 GB RAM and Intel(R) Core(TM) i5-1035G1 CPU@1.00 GHz with 12 GB RAM.
, \(\ell _{2}(\mathbb{R})\), and \(\mathcal{L}^{2}_{\mathbb{R}}(\Omega )\), where Ω is a closed bounded interval of \(\mathbb{R}\). Numerical experiments were carried out on MATLAB R2013a and R2020 versions. All programs were run on PCs with Intel(R) Core(TM)2 Duo CPU and 3 GB RAM and Intel(R) Core(TM) i5-1035G1 CPU@1.00 GHz with 12 GB RAM.
The accompanying parameters of the aforementioned methods employed in the experiments are presented in Table 1, whereas their numerical results and computation times are illustrated in Tables 2–9 and Figs. 1–7 in loglog plots. In these tables, p represents the dimension of the real line in Example 1, s denotes the index defined in the sequences given in Example 2 (see, e.g., Eq. (5.2)), N is the maximum number of iterations, and n is the index of each sequence. For experimental purpose, n is looped from 0 to N. The term \(\Vert u_{n} \Vert _{2} \) denotes the second norm at index n. In Example 3, j represents the number of partitions on \([0,1]\).
Example 1
Let \(f: \mathbb{R}^{p}\longrightarrow \mathbb{R}:x\mapsto \Vert x \Vert \). Then the subdifferential of f at x (see, e.g., [36]) is given by

It is well known that \(F=\partial f\) defined in (5.1) is maximal monotone. Also, define \(K:\mathbb{R}^{p}\longrightarrow \mathbb{R}^{p} \) by \(Kx=x\) for all  . Clearly, K is maximal monotone. Moreover, the only solution of the inclusion \(0\in u+KFu\) is \(u^{*}=0\). For BOY, the present algorithm, the initial points in \(\mathbb{R}^{p}\) are \(u_{1},v_{1},u_{2},v_{2}=(1,1,\ldots,1)\), whereas \(u_{1},v_{1}=(1,1,\ldots,1)\) in the other algorithms.
. Clearly, K is maximal monotone. Moreover, the only solution of the inclusion \(0\in u+KFu\) is \(u^{*}=0\). For BOY, the present algorithm, the initial points in \(\mathbb{R}^{p}\) are \(u_{1},v_{1},u_{2},v_{2}=(1,1,\ldots,1)\), whereas \(u_{1},v_{1}=(1,1,\ldots,1)\) in the other algorithms.
As tabulated in Table 2 and illustrated in Figs. 1–3, the present algorithm appears to be more efficient at approximating the zero of Eq. (5.1) as compared to others. In loops the presence of an inertial term leads to more computational time. However, as depicted in Table 3, the present algorithm—containing two inertial terms—still competes favorably with others.
Example 2
Define a map \(f:\ell _{2}(\mathbb{R}) \longrightarrow \mathbb{R} \) by \(f(x)= \Vert x \Vert \) for all \(x\in \ell _{2}(\mathbb{R})\). Then the subdifferential of f at \(x\in \ell _{2}(\mathbb{R})\) is given by
It is well known that \(F:=\partial f \) is maximal monotone. Also, define the map \(K:\ell _{2}(\mathbb{R})\rightarrow \ell _{2}(\mathbb{R})\) by \(Kx=2x \) for all \(x\in \ell _{2}(\mathbb{R})\). Obviously, K is monotone and bounded. Consider the points \(u_{1}:=\{u_{1,j}\}_{j=1}^{\infty }\), \(v_{1}:=\{v_{1,j}\}_{j=1}^{\infty }\), \(u_{2}:=\{u_{2,j}\}_{j=1}^{\infty }\), and \(v_{2}:=\{v_{2,j}\}_{j=1}^{\infty } \) defined by


where  ,
,  , and the ceiling
, and the ceiling  . Algorithm (3.1) uses the initial points defined in (5.2) and (5.3), whereas other algorithms are initialized by (5.2) only. Obviously, \(u_{1},u_{2},v_{1}\), and \(v_{2}\) are elements of \(\ell _{2}(\mathbb{R}) \). Numerical results are displayed in Tables 6 and 7, whereas graphical illustrations are presented in Figs. 9–7. During the experiment, the algorithm MM (1.17) becomes unstable, as this can be seen from its results in Table 6 and the figures. However, BOY (3.1) remains stable and competes favorably against others in terms of computational time (see Table 7), thus gaining advantage over others.
. Algorithm (3.1) uses the initial points defined in (5.2) and (5.3), whereas other algorithms are initialized by (5.2) only. Obviously, \(u_{1},u_{2},v_{1}\), and \(v_{2}\) are elements of \(\ell _{2}(\mathbb{R}) \). Numerical results are displayed in Tables 6 and 7, whereas graphical illustrations are presented in Figs. 9–7. During the experiment, the algorithm MM (1.17) becomes unstable, as this can be seen from its results in Table 6 and the figures. However, BOY (3.1) remains stable and competes favorably against others in terms of computational time (see Table 7), thus gaining advantage over others.
Example 3
In this example, we set \(\Omega =[0,1]\). Define \(F,K:\mathcal{L}_{2}^{\mathbb{R}}([0,1])\longrightarrow \mathcal{L}_{2}^{ \mathbb{R}}([0,1])\) by \((Fu)(t)=(t+1)u(t)\) and \((Ku)(t)=u(t)\) for all  . Then
. Then
Therefore F and K are monotone. It is also clear that F and K are linear and bounded. Thus by Theorem 3.5 they are maximal monotone. In this example, we choose \(u_{1}=(1+x^{2})^{-1}, v_{1}=x^{2}, u_{2}=x^{3}\), and \(v_{2}=\sin x \). For the purpose of experiment, the interval \([0,1]\) is partitioned into j subintervals. The numerical output and computational time for different number of iterations N and subintervals j can be seen in Tables 8 and 9, respectively. As illustrated in those tables and Figs. 8–10, the sequence produced by BOY (3.1) evidently converges faster than its pairs.
6 Conclusion
In this paper, we introduced a novel inertial algorithm for approximating solutions of Hammerstein inclusions  in Hilbert spaces. We also proved the strong convergence of the proposed scheme. Furthermore, we made no assumption of continuity in the main theorem. Moreover, the following observations were made:
in Hilbert spaces. We also proved the strong convergence of the proposed scheme. Furthermore, we made no assumption of continuity in the main theorem. Moreover, the following observations were made:
-
1.
The Inertial algorithm seems to display its efficiency when compared to the Noninertial algorithms, which perform poorly as the dimension and number of iterations increase.
-
2.
Convergence of the Inertial algorithm seems to be independent of the choice of \(u_{2} \) and \(v_{2} \).
-
3.
In sequence and function spaces the Inertial algorithm appears to be more effective and accurate.
-
4.
On
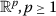 , the optimal choice of \(c_{n}\) appears to be zero.
, the optimal choice of \(c_{n}\) appears to be zero.
From the results obtained, the inertial algorithm would, perhaps, be preferred to the noninertial algorithms in any possible application.
Availability of data and materials
Data sharing is not applicable to this paper.
References
Alber, Y.I., Ryazantseva, I.: Nonlinear Ill Posed Problems of Monotone Type. Springer, London (2006)
Alvarez, F.: Weak convergence of a relaxed and inertial hybrid projection-proximal point algorithm for maximal monotone operators in Hilbert space. SIAM J. Optim. 14(3), 773–782 (2004) (electronic)
Appeli, J., De Pascale, E., Nguyêñ, H.T., Zabreĭko, P.P.: Nonlinear integral inclusions of Hammerstein type. Topol. Methods Nonlinear Anal. 5, 111–124 (1995)
Brézis, H., Browder, F.E.: Existence theorems for nonlinear integral equations of Hammerstein type. Bull. Am. Math. Soc. 81, 73–78 (1975)
Brézis, H., Browder, F.E.: Nonlinear integral equations and systems of Hammerstein type. Bull. Am. Math. Soc. 82, 115–147 (1976)
Brézis, H., Browder, F.E.: Some new results about Hammerstein equations. Bull. Am. Math. Soc. 80, 567–572 (1974)
Browder, F.E.: Nonlinear functional analysis and nonlinear integral equations of Hammerstein and Uryshon type. In: Contributions to Nonlinear Functional Analysis, pp. 425–500. Academic Press, San Diego (1971)
Browder, F.E.: Nonlinear mappings of nonexpansive and accretive type in Banach spaces. Bull. Am. Math. Soc. 73, 875–882 (1967)
Browder, F.E.: Nonlinear monotone and accretive operators in Banach space. Proc. Natl. Acad. Sci. USA 61, 388–393 (1968)
Browder, F.E.: The solvability of nonlinear functional equations. Duke Math. J. 30, 557–566 (1963)
Browder, F.E., De Figueiredo, D.G., Gupta, C.P.: Maximal monotone operators and nonlinear integral equations of Hammerstein type. Bull. Am. Math. Soc. 76, 700–705 (1970)
Browder, F.E., De Figueiredo, D.G.: Monotone nonlinear operators. Koukl. Nederl. Akad. Wetersch 69, 412–420 (1966)
Cardinali, T.S., Papageorgiou, N.S.: Hammerstein integral inclusion in reflexive Banach spaces. Proc. Am. Math. Soc. 124(2), 507–614 (1996)
Chepanovich, R.S.: Nonlinear Hammerstein equations and fixed points. Publ. Inst. Math. (Belgr.) 35, 119–123 (1984).
Chidume, C.E., Bello, A.U.: An iterative algorithm for approximating solutions of Hammerstein equations with monotone maps in Banach spaces. Appl. Math. Comput. 313, 408–417 (2017)
Chidume, C.E., Djitté, N.: Approximation of solutions of nonlinear integral equations of Hammerstein type. Int. Sch. Res. Not. 2012, Article ID 169751 (2012)
Chidume, C.E., Djitte, N.: Approximation of solutions of Hammerstein equations with bounded strongly accretive nonlinear operator. Nonlinear Anal. 70, 4071–4078 (2009)
Chidume, C.E., Djitte, N.: Convergence theorems for solutions of Hammerstein equations with accretive-type nonlinear operators. Panam. Math. J. 22(2), 19–29 (2012)
Chidume, C.E., Djitte, N.: Iterative approximation of solutions of nonlinear equations of Hammerstein-type. Nonlinear Anal. 70, 4086–4092 (2009)
Chidume, C.E., Ofeodu, E.U.: Solution of nonlinear integral equations of Hammerstein-type. Nonlinear Anal. 74, 4293–4299 (2011)
Chidume, C.E., Osilike, M.O.: Iterative solutions of nonlinear integral equations of Hammerstein-type. J. Niger. Math. Soc. 11, 9–18 (1992); Nonlinear Anal., Theory Methods Appl. 36, 863–872 (1999)
Chidume, C.E., Osilike, M.O.: Iterative solutions of nonlinear accretive operator equations in arbitrary Banach spaces. Nonlinear Anal. 36, 863–872 (1999)
Chidume, C.E., Shehu, Y.: Approximation of solutions of generalised equations of Hammerstein-type. Comput. Math. Appl. 63, 966–974 (2012)
Chidume, C.E., Shehu, Y.: Strong convergence theorem for approximation of solutions of equations of Hammerstein type. Nonlinear Anal., Theory Methods Appl. 75(14), 5664–5671 (2012). https://doi.org/10.1016/j.na.2012.05.014
Chidume, C.E., Shehu, Y.: Iterative approximation of solutions of equations of Hammerstein type in certain Banach spaces. Appl. Math. Comput. 219(10), 5657–5667 (2013). https://doi.org/10.1016/j.amc.2012.11.041
Chidume, C.E., Zegeye, H.: Approximation of solutions of nonlinear equations of Hammerstein-type in Hilbert space. Proc. Am. Math. Soc. 133(3), 851–858 (2005)
Chidume, C.E., Zegeye, H.: Approximation of solutions of nonlinear equations of monotone and Hammerstein-type. Appl. Anal. 82(8), 747–758 (2003)
Chidume, C.E., Zegeye, H.: Iterative approximation of solutions of nonlinear equation of Hammerstein-type. Abstr. Appl. Anal. 6, 353–367 (2003)
Clarke, F.H.: Optimization and Nonsmooth Analysis. Wiley, New York (1983)
Diekmann, O.: Thresholds and travelling waves for the geographical spread of infection. J. Math. Biol. 6, 109–130 (1978)
Doležal, V.: Monotone Operators and Its Applications in Automation and Network Theory. Studies in Automation and Control, vol. 3. Elsevier, New York (1979)
Maingé, P.E., Merabet, N.: A new inertial-type hybrid projection-proximal algorithm for monotone inclusions. Appl. Math. Comput. 215, 3149–3162 (2010).
Kamimura, S., Takahashi, W.: Approximating solutions of maximal monotone operators in Hilbert spaces. J. Approx. Theory 106, 226–240 (2000)
Kato, T.: Nonlinear semigroups and evolution equations. J. Math. Soc. Jpn. 19, 508–520 (1967)
Mann, W.R.: Mean value methods in iteration. Proc. Am. Math. Soc. 4, 506–510 (1953)
Minjibir, M.S., Mohammed, I.: Iterative solutions of Hammerstein integral inclusions. Appl. Math. Comput. 320, 389–399 (2018)
Moudafi, A., Elissabeth, E.: Approximate inertial proximal methods using the enlargement of maximal monotone operators. Int. J. Pure Appl. Math. 5(3), 283–299 (2003)
Pascali, D., Sburian, S.: Nonlinear Mappings of Monotone Type. Editura Academia, Bucuresti (1978)
Poljak, B.T.: Some methods of speeding up the convergence of iterative methods. Zh. Vychisl. Mat. Mat. Fiz. 4, 791–803 (1964)
Reich, S.: Strong convergence theorems for resolvents of accretive operators in Banach spaces. J. Math. Anal. Appl. 75(1), 287–292 (1980)
Shehu, Y.: Strong convergence theorem for integral equations of Hammerstein type in Hilbert spaces. Appl. Math. Comput. 231, 140–147 (2014). https://doi.org/10.1016/j.amc.2013.12.157
Thieme, H.R.: Density-dependent regulation of spatially distributed populations and their asymptotic speed of spread. J. Math. Biol. 8, 173–187 (1979)
Xu, H.K.: Iterative algorithms for nonlinear operators. J. Lond. Math. Soc. 66(2), 240–256 (2002)
Acknowledgements
The authors appreciate the support of their institution and AfDB. Also, the authors are grateful to the anonymous referees and the editor for their valuable comments and suggestions, which helped to improve the quality of this paper.
Funding
This work is supported from AfDB Research Grant Funds to AUST.
Author information
Authors and Affiliations
Contributions
All authors contributed equally. All authors read and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Bello, A.U., Omojola, M.T. & Yahaya, J. An inertial-type algorithm for approximation of solutions of Hammerstein integral inclusions in Hilbert spaces. Fixed Point Theory Algorithms Sci Eng 2021, 8 (2021). https://doi.org/10.1186/s13663-021-00691-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13663-021-00691-7










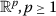 , the optimal choice of
, the optimal choice of