- Research
- Open access
- Published:
On the convergence of iteration processes for semigroups of nonlinear mappings inmodular function spaces
Fixed Point Theory and Applications volume 2015, Article number: 3 (2015)
Abstract
Let C be a ρ-bounded, ρ-closed, convexsubset of a modular function space 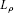 . We investigate the problem of constructingcommon fixed points for asymptotic pointwise nonexpansive semigroups of mappings
. We investigate the problem of constructingcommon fixed points for asymptotic pointwise nonexpansive semigroups of mappings , i.e. a family such that
, i.e. a family such that ,
,  , and
, and  , where
, where  , for every
, for every 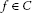 .
.
MSC: 47H09, 46B20, 47H10, 47E10.
1 Introduction
In 2008, Kirk and Xu [1] studied existence of fixed points of asymptotic pointwise nonexpansivemappings  , i.e.
, i.e.

where  , for all
, for all  . Their main result (Theorem 3.5) states thatevery asymptotic pointwise nonexpansive self-mapping of a nonempty, closed, boundedand convex subset C of a uniformly convex Banach space X has afixed point. As pointed out by Kirk and Xu, asymptotic pointwise mappings seem to bea natural generalization of nonexpansive mappings. The conditions on
. Their main result (Theorem 3.5) states thatevery asymptotic pointwise nonexpansive self-mapping of a nonempty, closed, boundedand convex subset C of a uniformly convex Banach space X has afixed point. As pointed out by Kirk and Xu, asymptotic pointwise mappings seem to bea natural generalization of nonexpansive mappings. The conditions on can be for instance expressed in terms of thederivatives of iterations of T for differentiable T. In 2009,these results were generalized by Hussain and Khamsi to metric spaces [2]. In 2011, Khamsi and Kozlowski [3] extended their result proving the existence of fixed points of asymptoticpointwise ρ-nonexpansive mappings acting in modular function spaces.The existence of common fixed points of semigroups of nonexpansive (in a modularsense) mappings acting in modular function spaces was first established by Kozlowskiin [4] and then extended to the semigroups of asymptotic pointwise nonexpansivemappings by the authors in [5]. The proof of this important theorem is of the existential nature anddoes not describe any algorithm for constructing a common fixed point of anasymptotic pointwise ρ-nonexpansive semigroup. The current paper aimsat filling this gap. The results of this paper generalize the convergence ofgeneralized Mann processes to common fixed points of semigroups of nonexpansivesemigroups studied in the recent paper by Bin Dehaish and Kozlowski [6].
can be for instance expressed in terms of thederivatives of iterations of T for differentiable T. In 2009,these results were generalized by Hussain and Khamsi to metric spaces [2]. In 2011, Khamsi and Kozlowski [3] extended their result proving the existence of fixed points of asymptoticpointwise ρ-nonexpansive mappings acting in modular function spaces.The existence of common fixed points of semigroups of nonexpansive (in a modularsense) mappings acting in modular function spaces was first established by Kozlowskiin [4] and then extended to the semigroups of asymptotic pointwise nonexpansivemappings by the authors in [5]. The proof of this important theorem is of the existential nature anddoes not describe any algorithm for constructing a common fixed point of anasymptotic pointwise ρ-nonexpansive semigroup. The current paper aimsat filling this gap. The results of this paper generalize the convergence ofgeneralized Mann processes to common fixed points of semigroups of nonexpansivesemigroups studied in the recent paper by Bin Dehaish and Kozlowski [6].
Let us recall that modular function spaces are a natural generalization of bothfunction and sequence variants of many spaces like Lebesgue, Orlicz,Musielak-Orlicz, Lorentz, Orlicz-Lorentz, Calderon-Lozanovskii spaces and manyothers, important from an applications perspective; see the book by Kozlowski [7] for an extensive list of examples and special cases. There exists anextensive literature on the topic of the fixed point theory in modular functionspaces; see e.g.[3, 7–18] and the references therein. It is also worthwhile mentioning a growinginterest in applications of the methods of the fixed point theory to semigroups ofnonlinear mappings and applications to the area of differential and integralequations (see e.g.[10, 19, 20]).
It is well known that the fixed point construction iteration processes forgeneralized nonexpansive mappings have been successfully used to develop efficientand powerful numerical methods for solving various nonlinear equations andvariational problems, often of great importance for applications in various areas ofpure and applied science. There exists an extensive literature on the subject ofiterative fixed point construction processes for asymptotically nonexpansivemappings in Hilbert, Banach, and metric spaces; see e.g.[2, 21–37] and the references therein. Kozlowski proved convergence to a fixed pointof some iterative algorithms of asymptotic pointwise nonexpansive mappings in Banachspaces [38] and the existence of common fixed points of semigroups of pointwiseLipschitzian mappings in Banach spaces [39]. Recently, the weak and strong convergence of such processes to commonfixed points of semigroups of mappings in Banach spaces was demonstrated byKozlowski and Sims [40] and by Kozlowski in [41].
We would like to emphasize that all convergence theorems proved in this paper defineconstructive algorithms that can be actually implemented. When dealing with specificapplications of these theorems, one should take into consideration how additionalproperties of the mappings, sets, and modulars involved can influence the actualimplementation of the algorithms defined in this paper.
2 Preliminaries
Let us introduce basic notions related to modular function spaces and relatednotation which will be used in this paper. For further details we refer the readerto preliminary sections of the recent articles [3, 6, 16] or to the survey article [17]; see also [7, 42, 43] for the standard framework of modular function spaces.
Let Ω be a nonempty set and Σ be a nontrivial σ-algebra ofsubsets of Ω. Let  be a δ-ring of subsets of Ω, such that
be a δ-ring of subsets of Ω, such that for any
for any  and
and  . Let us assume that there exists an increasingsequence of sets
. Let us assume that there exists an increasingsequence of sets  such that
such that  . By ℰ we denote the linear space of all simplefunctions with supports from
. By ℰ we denote the linear space of all simplefunctions with supports from  . By
. By we will denote the space of all extended measurablefunctions, i.e. all functions
we will denote the space of all extended measurablefunctions, i.e. all functions  such that there exists a sequence
such that there exists a sequence ,
,  and
and  for all
for all  . By
. By  we denote the characteristic function of the setA.
we denote the characteristic function of the setA.
Definition 2.1[7]
Let  be a nontrivial, convex and even function. We saythat ρ is a regular convex function pseudomodular if
be a nontrivial, convex and even function. We saythat ρ is a regular convex function pseudomodular if
-
(i)
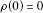 ;
; -
(ii)
ρ is monotone, i.e.
 for all
for all  implies
implies 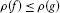 , where
, where 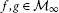 ;
; -
(iii)
ρ is orthogonally subadditive, i.e.
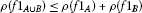 for any
for any 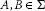 such that
such that 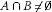 ,
, 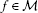 ;
; -
(iv)
ρ has the Fatou property, i.e.
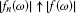 for all
for all  implies
implies 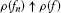 , where
, where  ;
; -
(v)
ρ is order continuous in ℰ, i.e.
 and
and  implies
implies  .
.
Similarly to the case of measure spaces, we say that a set  is ρ-null if
is ρ-null if  for every
for every  . We say that a property holds ρ-almosteverywhere if the exceptional set is ρ-null. As usual we identify anypair of measurable sets whose symmetric difference is ρ-null as wellas any pair of measurable functions differing only on a ρ-null set.With this in mind we define
. We say that a property holds ρ-almosteverywhere if the exceptional set is ρ-null. As usual we identify anypair of measurable sets whose symmetric difference is ρ-null as wellas any pair of measurable functions differing only on a ρ-null set.With this in mind we define  , where each element is actually an equivalence classof functions equal ρ-a.e. rather than an individual function.
, where each element is actually an equivalence classof functions equal ρ-a.e. rather than an individual function.
Definition 2.2[7]
We say that a regular function pseudomodular ρ is a regular convexfunction modular if  implies
implies  ρ-a.e. The class of all nonzero regular convex function modularsdefined on Ω will be denoted by ℜ.
ρ-a.e. The class of all nonzero regular convex function modularsdefined on Ω will be denoted by ℜ.
Let ρ be a convex function modular. A modular function space is thevector space  . In the vector space
. In the vector space 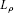 , the following formula:
, the following formula:

defines a norm, frequently called the Luxemburg norm.
The following notions will be used throughout the paper.
Definition 2.4[8]
Let  .
.
-
(a)
We say that
 is ρ-convergent to f and write
is ρ-convergent to f and write 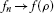 if and only if
if and only if 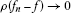 .
. -
(b)
A sequence
 , where
, where 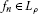 , is called ρ-Cauchy if
, is called ρ-Cauchy if 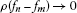 as
as  .
. -
(c)
We say that
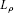 is ρ-complete if and only if any ρ-Cauchy sequence in
is ρ-complete if and only if any ρ-Cauchy sequence in 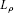 is ρ-convergent.
is ρ-convergent. -
(d)
A set
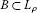 is called ρ-closed if for any sequence of
is called ρ-closed if for any sequence of 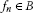 , the convergence
, the convergence 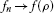 implies that f belongs to B.
implies that f belongs to B. -
(e)
A set
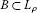 is called ρ-bounded if
is called ρ-bounded if  .
.
Since ρ fails in general the triangle identity, many of the knownproperties of limit may not extend to ρ-convergence. For example,ρ-convergence does not necessarily imply theρ-Cauchy condition. However, it is important to remember that theρ-limit is unique when it exists. The following proposition bringstogether a few facts, which will be often used in the proofs of our results.
Proposition 2.1[7]
Let .
.
-
(i)
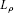 isρ-complete.
isρ-complete. -
(ii)
ρ-Balls
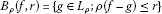 areρ-closed.
areρ-closed. -
(iii)
If
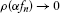 for an
for an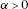 then there exists a subsequence
then there exists a subsequence of
of such that
such that ρ-a.e.
ρ-a.e. -
(iv)
 whenever
whenever ρ-a.e. (note: this property is equivalent to the Fatou property).
ρ-a.e. (note: this property is equivalent to the Fatou property).
Let us recall the definition of an asymptotic pointwise nonexpansive mapping actingin a modular function space.
Definition 2.5[3]
Let  and let
and let  be nonempty and ρ-closed. A mapping
be nonempty and ρ-closed. A mapping is called
is called
-
(i)
a pointwise Lipschitzian mapping if there exists
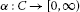 such that
such that 
-
(ii)
an asymptotic pointwise nonexpansive if there exists a sequence of mappings
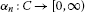 such that
such that 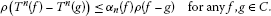
and  for any
for any  .
.
A point 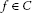 is called a fixed point of T whenever
is called a fixed point of T whenever . The set of fixed points of T will bedenoted by
. The set of fixed points of T will bedenoted by  .
.
Define  , where
, where  , for any
, for any 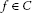 and
and  . Clearly then
. Clearly then

Definition 2.6 Define  as a class of all asymptotic pointwise nonexpansivemappings T such that
as a class of all asymptotic pointwise nonexpansivemappings T such that


The notion of the asymptotic pointwise nonexpansiveness will be now extended to aone-parameter family of mappings. Throughout this paper J will be thesemigroup of all nonnegative numbers, that is,  with normal addition.
with normal addition.
Definition 2.7 A one-parameter family  of mappings from C into itself is said to bean asymptotic pointwise nonexpansive semigroup on C if ℱ satisfiesthe following conditions:
of mappings from C into itself is said to bean asymptotic pointwise nonexpansive semigroup on C if ℱ satisfiesthe following conditions:
-
(i)
 for
for 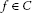 ;
; -
(ii)
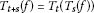 for
for 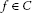 and
and  ;
; -
(iii)
for each
 ,
, 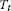 is an asymptotic pointwise nonexpansive mapping, i.e. there exists a function
is an asymptotic pointwise nonexpansive mapping, i.e. there exists a function 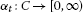 such that
such that  (2.4)
(2.4)
such that  for every
for every 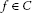 ;
;
-
(iv)
for each
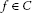 , the mapping
, the mapping 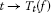 is ρ-continuous.
is ρ-continuous.
For each  let
let  denote the set of its fixed points. Define then theset of all common fixed points set for mappings from ℱ as the followingintersection:
denote the set of its fixed points. Define then theset of all common fixed points set for mappings from ℱ as the followingintersection:

The common fixed points are frequently interpreted as the stationary points of thesemigroup ℱ. Note that without loss of generality we may assume for any
for any  and
and 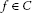 and
and  .
.
Denoting  and
and  for
for  , we note that without loss of generality we canassume that ℱ is asymptotically nonexpansive if
, we note that without loss of generality we canassume that ℱ is asymptotically nonexpansive if


Define  . Note that
. Note that

The above notation will be consistently used throughout this paper.
Definition 2.8 By  we will denote the class of all asymptotic pointwisenonexpansive semigroups on C such that
we will denote the class of all asymptotic pointwisenonexpansive semigroups on C such that


Note that we do not assume that all functions  are bounded by a common constant. Therefore, we donot assume that ℱ is uniformly Lipschitzian.
are bounded by a common constant. Therefore, we donot assume that ℱ is uniformly Lipschitzian.
Definition 2.9 We will say that a semigroup  is ρ continuous if
is ρ continuous if

for any 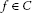 and
and  .
.
The concept ρ-type is a powerful technical tool which is used in theproofs of many fixed point results. The definition of a ρ-type isbased on a given sequence. In this work, we generalize this definition to be adaptedto one-parameter family of mappings.
Definition 2.10 Let  be convex and ρ-bounded.
be convex and ρ-bounded.
-
(1)
A function
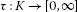 is called a ρ-type (or shortly a type) if there exists a one-parameter family
is called a ρ-type (or shortly a type) if there exists a one-parameter family  of elements of K such that for any
of elements of K such that for any 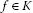 we have
we have 
-
(2)
Let τ be a ρ-type. A sequence
 is called a minimizing sequence of τ if
is called a minimizing sequence of τ if 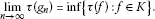
Note that τ is convex provided ρ is convex.
Let us recall the modular equivalents of uniform convexity introduced in [3].
Definition 2.11 Let  . We define the following uniform convexity (UC) typeproperties of the function modular ρ:
. We define the following uniform convexity (UC) typeproperties of the function modular ρ:
-
(i)
Let
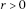 ,
,  . Define
. Define 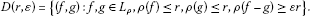
Let

and  if
if  . We say that ρ satisfies (UC) if forevery
. We say that ρ satisfies (UC) if forevery 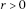 ,
,  ,
,  . Note that for every
. Note that for every 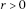 ,
,  , for
, for  small enough.
small enough.
-
(ii)
We say that ρ satisfies (UUC1) if there exists
 , for every
, for every 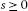 , and
, and  such that
such that 
We will need the following result, being a modular equivalent of a norm property inuniformly convex Banach spaces; see e.g.[26].
Lemma 2.1[6]
Let be (UUC1) and let
be (UUC1) and let be bounded away from 0 and 1. If there exists
be bounded away from 0 and 1. If there exists such that
such that


then

The following property plays in the theory of modular function space a role similarto the reflexivity in Banach spaces; see e.g.[9].
Definition 2.12 We say that 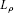 has property
has property  if and only if every nonincreasing sequence
if and only if every nonincreasing sequence of nonempty, ρ-bounded,ρ-closed, and convex subsets of
of nonempty, ρ-bounded,ρ-closed, and convex subsets of 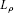 has nonempty intersection.
has nonempty intersection.
Similarly to the Banach space case, the modular uniform convexity implies property .
.
Theorem 2.1[3]
Let be (UUC1) then
be (UUC1) then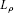 has property
has property .
.
The next lemma is a generalization of the minimizing sequence property for typesdefined by sequences in Lemma 4.3 in [16] to the one-parameter semigroup case.
Lemma 2.2[5]
Assume is (UUC1). LetCbe a nonempty, ρ-bounded,ρ-closed, and convex subset of
is (UUC1). LetCbe a nonempty, ρ-bounded,ρ-closed, and convex subset of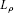 . Letτbe a type defined by a one-parameter family
. Letτbe a type defined by a one-parameter family inC.
inC.
-
(i)
If
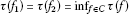 , then
, then .
. -
(ii)
Any minimizing sequence
 ofτisρ-convergent. Moreover, theρ-limit of
ofτisρ-convergent. Moreover, theρ-limit of is independent of the minimizing sequence.
is independent of the minimizing sequence.
Using Lemma 2.2, the authors proved the following common fixed point result forasymptotic pointwise nonexpansive semigroups.
Theorem 2.2[5]
Assume is (UUC1). LetCbe aρ-closed, ρ-bounded, convex,and nonempty subset. Let
is (UUC1). LetCbe aρ-closed, ρ-bounded, convex,and nonempty subset. Let be an asymptotic pointwise nonexpansive semigroup onC. Then ℱ has a common fixed point and the set
be an asymptotic pointwise nonexpansive semigroup onC. Then ℱ has a common fixed point and the set of common fixed points isρ-closed and convex.
of common fixed points isρ-closed and convex.
3 The demiclosedness principle
In this section we will use the notion the uniform continuity of the function modularρ in the sense of the following definition (see e.g.[16]).
Definition 3.1 We say that  is uniformly continuous if for every
is uniformly continuous if for every and
and  , there exists
, there exists  such that
such that

provided  and
and  .
.
Let us mention that the uniform continuity holds for a large class of functionmodulars. For instance, it can be proved that in Orlicz spaces over a finiteatomless measure [44] or in Orlicz sequence spaces [45] the uniform continuity of the Orlicz modular is equivalent to the -type condition. Recall that ρ satisfiesthe
-type condition. Recall that ρ satisfiesthe  -type condition if and only if there exists
-type condition if and only if there exists such that
such that  , for any
, for any  .
.
Let us recall the definition of the Opial property and the strong Opial property inmodular function spaces [16, 46].
Definition 3.2 We say that 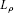 satisfies the ρ-a.e. Opial property iffor every
satisfies the ρ-a.e. Opial property iffor every  which is ρ-a.e. convergent to 0 suchthat there exists a
which is ρ-a.e. convergent to 0 suchthat there exists a  for which
for which

the following inequality holds for any  not equal to 0:
not equal to 0:

Definition 3.3 We say that 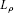 satisfies the ρ-a.e. strong Opialproperty if for every
satisfies the ρ-a.e. strong Opialproperty if for every  which is ρ-a.e. convergent to 0 suchthat there exists a
which is ρ-a.e. convergent to 0 suchthat there exists a  for which
for which

the following equality holds for any  :
:

Remark 3.1 Note that the ρ-a.e. strong Opial property impliesthe ρ-a.e. Opial property [46].
Remark 3.2 Also, note that, by virtue of Theorem 2.1 in [46], every convex, orthogonally additive function modular ρ hasthe ρ-a.e. strong Opial property. Let us recall that ρis called orthogonally additive if  whenever
whenever  . Therefore, all Orlicz and Musielak-Orlicz spacesmust have the strong Opial property.
. Therefore, all Orlicz and Musielak-Orlicz spacesmust have the strong Opial property.
Note that the Opial property in the norm sense does not necessarily hold for severalclassical Banach function spaces. For instance the norm Opial property does not holdfor  spaces for
spaces for  , while the modular strong Opial property holds in
, while the modular strong Opial property holds in for all
for all  .
.
Lemma 3.1[4]
Let . Assume that
. Assume that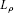 has theρ-a.e. strong Opial property. Let
has theρ-a.e. strong Opial property. Let be a nonempty, stronglyρ-bounded, andρ-a.e. compact convex set. Thenanyρ-type defined in C attains its minimum inC.
be a nonempty, stronglyρ-bounded, andρ-a.e. compact convex set. Thenanyρ-type defined in C attains its minimum inC.
To begin our discussion of the demiclosedness principle, let us quote the followingversion of this theorem applied to the asymptotic pointwise nonexpansive mappings [[6], Theorem 4.1].
Theorem 3.1 (Demiclosedness principle)
Let . Assume that
. Assume that
-
(1)
ρis (UUC1),
-
(2)
ρhas the strong Opial property,
-
(3)
ρhas the
 property and is uniformly continuous.
property and is uniformly continuous.
Let be nonempty, convex, stronglyρ-bounded, andρ-closed, and let
be nonempty, convex, stronglyρ-bounded, andρ-closed, and let . Let
. Let , and
, and . If
. If ρ-a.e. and
ρ-a.e. and , then
, then .
.
We will need a version of the above theorem without assuming that . This will require a different proof, which issketched below.
. This will require a different proof, which issketched below.
Theorem 3.2Let . Assume that
. Assume that
-
(1)
ρis (UUC1),
-
(2)
ρhas the strong Opial property,
-
(3)
ρhas the
 property and is uniformly continuous.
property and is uniformly continuous.
Let be nonempty, convex, stronglyρ-bounded, andρ-closed. Let
be nonempty, convex, stronglyρ-bounded, andρ-closed. Let be an asymptotic pointwise nonexpansive mapping such that
be an asymptotic pointwise nonexpansive mapping such that

and for any
for any . We will assume the functions
. We will assume the functions are bounded onC, i.e. Tis uniformlyρ-Lipschitzian mapping. Let
are bounded onC, i.e. Tis uniformlyρ-Lipschitzian mapping. Let , and
, and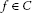 . If
. If ρ-a.e. and
ρ-a.e. and , then
, then . In particular, we have
. In particular, we have .
.
Proof Define the ρ-type function

Note that

Indeed, we have

which implies

for any  , where
, where  . Hence
. Hence

Since ρ has the  property, we get
property, we get

Since ρ is uniformly continuous, we get

for any  and
and  . In particular, we have
. In particular, we have

In other words, we have  , for any
, for any  . Since ρ has the Opial property, it iseasy to prove that
. Since ρ has the Opial property, it iseasy to prove that

Since T is an asymptotic pointwise nonexpansive mapping, we get

Since ρ is (UUC1), then arguing similarly to the proof ofTheorem 4.1 in [6], we have

Since T is ρ-continuous, we get  , i.e.
, i.e. . □
. □
As a corollary to this result, we get the following important result.
Corollary 3.1Let . Assume that
. Assume that
-
(1)
ρis (UUC1),
-
(2)
ρhas the strong Opial property,
-
(3)
ρhas the
 property and is uniformly continuous.
property and is uniformly continuous.
Let be nonempty, convex, stronglyρ-bounded, andρ-closed. Let
be nonempty, convex, stronglyρ-bounded, andρ-closed. Let be asymptotic pointwise nonexpansive mappings such that
be asymptotic pointwise nonexpansive mappings such that

for any , with
, with , and
, and , for any
, for any . We will assume the functions
. We will assume the functions and
and are bounded onC. Let
are bounded onC. Let , and
, and . If
. If ρ-a.e. and
ρ-a.e. and

then . In particular, we have
. In particular, we have .
.
The above results lead us to the following version of the demiclosedness principlefor semigroup of mappings.
Theorem 3.3 (Demiclosedness principle)
Let . Assume that
. Assume that
-
(1)
ρis (UUC1),
-
(2)
ρhas the strong Opial property,
-
(3)
ρhas the
 property and is uniformly continuous.
property and is uniformly continuous.
Let be nonempty, convex, stronglyρ-bounded, andρ-closed, and let
be nonempty, convex, stronglyρ-bounded, andρ-closed, and let be continuous. Let
be continuous. Let , and
, and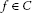 . Assume
. Assume ρ-a.e. If there exist
ρ-a.e. If there exist such that
such that is irrational and
is irrational and

then .
.
Proof In view of Corollary 3.1, we know that

Let us denote  . Note that for any
. Note that for any  we have
we have

Combining the above we get

Since  is irrational, then the set
is irrational, then the set  is dense in
is dense in  [47]. Since ℱ is continuous and ρ is uniformly continuous,we have
[47]. Since ℱ is continuous and ρ is uniformly continuous,we have

Hence  as desired. □
as desired. □
4 Convergence of generalized Krasnosel’skii-Mann iteration processes
Let us start with the precise definition of the generalized Krasnosel’skii-Manniteration process for semigroups of nonlinear mappings.
Definition 4.1 Let  ,
,  and
and  . The generalized Krasnosel’skii-Mann iterationprocess
. The generalized Krasnosel’skii-Mann iterationprocess  generated by the semigroup ℱ, the sequences
generated by the semigroup ℱ, the sequences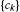 and
and  , is defined by the following iterative formula:
, is defined by the following iterative formula:

and
-
(1)
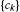 is bounded away from 0 and 1,
is bounded away from 0 and 1, -
(2)
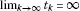 ,
, -
(3)
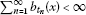 for every
for every  .
.
Definition 4.2 We say that a generalized Krasnosel’skii-Mann iterationprocess  is well defined if
is well defined if

Arguing exactly like in the proof of Lemma 5.2 in [6] (see also Lemma 22.20 in [40]), we get the following result.
Lemma 4.1Let be (UUC1). Let
be (UUC1). Let be aρ-closed, ρ-bounded, and convexset. Let
be aρ-closed, ρ-bounded, and convexset. Let ,
,  , and let
, and let be a sequence generated by a generalized Krasnosel’skii-Mannprocess
be a sequence generated by a generalized Krasnosel’skii-Mannprocess . Then there exists an
. Then there exists an such that
such that .
.
We will prove now a generic version of the convergence theorem for the sequences which are generated by the Krasnosel’skii-Manniteration process and are at the same time approximate fixed point sequences.
which are generated by the Krasnosel’skii-Manniteration process and are at the same time approximate fixed point sequences.
Theorem 4.1Let . Assume that
. Assume that
-
(1)
ρis (UUC1),
-
(2)
ρhas the strong Opial property,
-
(3)
ρhas the
 property and is uniformly continuous.
property and is uniformly continuous.
Let be nonempty, ρ-a.e. compact,convex, stronglyρ-bounded, andρ-closed, and let
be nonempty, ρ-a.e. compact,convex, stronglyρ-bounded, andρ-closed, and let . Assume that
. Assume that is a well defined Krasnosel’skii-Mann iteration process.If for the sequence
is a well defined Krasnosel’skii-Mann iteration process.If for the sequence generated by
generated by we have
we have

where are such that
are such that is irrational, then
is irrational, then convergesρ-a.e. to a common fixed point
convergesρ-a.e. to a common fixed point .
.
Proof Observe that by Theorem 2.2 the set of fixed points is nonempty, convex and ρ-closed.Consider
is nonempty, convex and ρ-closed.Consider  , two ρ-a.e. cluster points of
, two ρ-a.e. cluster points of . There exits then
. There exits then  ,
,  subsequences of
subsequences of  such that
such that  ρ-a.e., and
ρ-a.e., and  ρ-a.e. It follows from Theorem 3.3 that
ρ-a.e. It follows from Theorem 3.3 that  and
and  . By Lemma 4.1, there exist
. By Lemma 4.1, there exist such that
such that

We claim that  . Assume to the contrary that
. Assume to the contrary that  . Then by the Opial property we have
. Then by the Opial property we have

The contradiction implies that  . Therefore,
. Therefore,  has at most one ρ-a.e. cluster point.Since C is ρ-a.e. compact it follows that the sequence
has at most one ρ-a.e. cluster point.Since C is ρ-a.e. compact it follows that the sequence has exactly one ρ-a.e. cluster point
has exactly one ρ-a.e. cluster point , which means that
, which means that  ρ-a.e. Applying the demiclosedness principle again, we get
ρ-a.e. Applying the demiclosedness principle again, we get . By the same argument, we get
. By the same argument, we get  (observe that the construction of w did notdepend on the selection of
(observe that the construction of w did notdepend on the selection of  ). From the density of
). From the density of  in
in  , we conclude that
, we conclude that  for any
for any  , as claimed. □
, as claimed. □
Let us apply the above result to some more specific situations. First we need toprove a series of axillary results. Let us start with the following elementarylemma.
Lemma 4.2[31]
Suppose
 is a bounded sequence of real numbers and
is a bounded sequence of real numbers and
 is a double index sequence of real numbers which satisfy
is a double index sequence of real numbers which satisfy

for each . Then
. Then converges to an
converges to an .
.
The following result provides an important technique which will be used in thispaper.
Lemma 4.3Let be (UUC1). Let
be (UUC1). Let be aρ-closed, ρ-bounded, and convexset. Let
be aρ-closed, ρ-bounded, and convexset. Let . Assume thatwis a common fixed point of ℱ. Let us denote by
. Assume thatwis a common fixed point of ℱ. Let us denote by a sequence generated by the generalized Krasnosel’skii-Mannprocess
a sequence generated by the generalized Krasnosel’skii-Mannprocess . Then there exists
. Then there exists such that
such that

Proof Let  . Since
. Since

it follows that for every  ,
,

Denote  for every
for every  and
and  . Observe that by the assumptions on the sequence
. Observe that by the assumptions on the sequence ,
,  . By Lemma 4.2, there exists an
. By Lemma 4.2, there exists an such that
such that  , as claimed. □
, as claimed. □
Lemma 4.4Let be (UUC1). Let
be (UUC1). Let be aρ-closed, ρ-bounded, and convexset, and
be aρ-closed, ρ-bounded, and convexset, and . Let
. Let be a generalized Krasnosel’skii-Mann iteration process.Then
be a generalized Krasnosel’skii-Mann iteration process.Then

and

Proof By Theorem 2.2, ℱ has at least one common fixed point . In view of Lemma 4.3, there exists
. In view of Lemma 4.3, there exists such that
such that

Note that

and that

Set  ,
,  , and note that
, and note that  by (4.10), and
by (4.10), and  by (4.11). Observe also that
by (4.11). Observe also that

Hence, it follows from Lemma 2.1 that

which by the construction of the sequence  is equivalent to
is equivalent to

as claimed. □
Lemma 4.5Let be (UUC1) and have the
be (UUC1) and have the property. Let
property. Let be aρ-closed, ρ-bounded, and convexset and let
be aρ-closed, ρ-bounded, and convexset and let . Denote by
. Denote by the sequence generated by a well defined generalizedKrasnosel’skii-Mann process
the sequence generated by a well defined generalizedKrasnosel’skii-Mann process . Let
. Let be such that for every
be such that for every there exists a strictly increasing sequence of natural numbers
there exists a strictly increasing sequence of natural numbers satisfying the following conditions:
satisfying the following conditions:
-
(a)
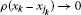 as
as ,
, -
(b)
 , where
, where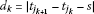 .
.
Then is an approximate fixed point sequence for all mappings
is an approximate fixed point sequence for all mappings where
where , that is,
, that is,

for every .
.
Proof Let us fix  . Note that
. Note that

By  , it suffices to prove that
, it suffices to prove that

To this end observe that

in view of the assumption (a) and by (4.9) in Lemma 4.4. Observe that

Indeed,

which tends to zero as  because of (4.17), Lemma 4.4, the fact that theprocess is well defined, assumptions (b) and (2.9), and the boundedness of eachfunction
because of (4.17), Lemma 4.4, the fact that theprocess is well defined, assumptions (b) and (2.9), and the boundedness of eachfunction  . This convergence gives us, via
. This convergence gives us, via , the required (4.20). On the other hand,
, the required (4.20). On the other hand,

which tends to zero as  because of assumption (a), Lemma 4.4, (4.20),the fact that the process is well defined, and the fact that the semigroup isasymptotic pointwise nonexpansive. Since ρ has the
because of assumption (a), Lemma 4.4, (4.20),the fact that the process is well defined, and the fact that the semigroup isasymptotic pointwise nonexpansive. Since ρ has the property,
property,

which completes the proof of the lemma. □
The following theorem is an immediate consequence of Lemma 4.5 andTheorem 4.1.
Theorem 4.2Let be uniformly continuous function modular satisfying (UUC1).Assume in addition thatρsatisfies
be uniformly continuous function modular satisfying (UUC1).Assume in addition thatρsatisfies and has the strong Opial property. Let
and has the strong Opial property. Let be aρ-closed, ρ-bounded, and convexset and let
be aρ-closed, ρ-bounded, and convexset and let . Denote by
. Denote by the sequence generated by a well defined generalizedKrasnosel’skii-Mann process
the sequence generated by a well defined generalizedKrasnosel’skii-Mann process . Let
. Let be such that
be such that is irrational and that there exists a strictly increasing sequence of naturalnumbers
is irrational and that there exists a strictly increasing sequence of naturalnumbers satisfying the following conditions:
satisfying the following conditions:
-
(a)
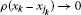 as
as ,
, -
(b)
 , where
, where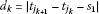 ,
, -
(c)
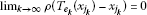 , where
, where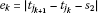 .
.
Then the sequence convergesρ-a.e. to a common fixed point
convergesρ-a.e. to a common fixed point .
.
Remark 4.1 Observe that a sequence  satisfying assumptions of Theorem 4.2 can bealways constructed. The main difficulty is in ensuring that the correspondingprocess
satisfying assumptions of Theorem 4.2 can bealways constructed. The main difficulty is in ensuring that the correspondingprocess  is well defined.
is well defined.
The next result answers the question when the sequence generated by the generalizedKrasnosel’skii-Mann process will converge strongly to a common fixed point.Not surprisingly we need to add a compactness assumption.
Theorem 4.3Under the assumptions of Theorem 4.2, if in additionCis assumed to beρ-compact, then the sequence generated by
generated by converges strongly to a common fixed point
converges strongly to a common fixed point , that is,
, that is,

Proof It follows from Theorem 4.2 that there exists a common fixedpoint  such that
such that  converges ρ-a.e. Byρ-compactness of C there exist
converges ρ-a.e. Byρ-compactness of C there exist  and a subsequence
and a subsequence  of
of  such that
such that

By Proposition 2.1 there exists a subsequence  of
of  such that
such that

By the uniqueness of the ρ-a.e. limit we get  . Hence
. Hence

On the other hand, the limit  exists by Lemma 4.3, which implies that
exists by Lemma 4.3, which implies that

as claimed. □
Remark 4.2 Observe that in view of the  assumption, the ρ-compactness of theset C assumed in Theorem 4.3 is equivalent to the compactness in thesense of the norm defined by ρ.
assumption, the ρ-compactness of theset C assumed in Theorem 4.3 is equivalent to the compactness in thesense of the norm defined by ρ.
References
Kirk WA, Xu HK: Asymptotic pointwise contractions.Nonlinear Anal. 2008, 69:4706–4712. 10.1016/j.na.2007.11.023
Hussain N, Khamsi MA: On asymptotic pointwise contractions in metric spaces.Nonlinear Anal. 2009,71(10):4423–4429. 10.1016/j.na.2009.02.126
Khamsi MA, Kozlowski WM: On asymptotic pointwise nonexpansive mappings in modular function spaces.J. Math. Anal. Appl. 2011,380(2):697–708. 10.1016/j.jmaa.2011.03.031
Kozlowski WM: On the existence of common fixed points for semigroups of nonlinear mappingsin modular function spaces.Comment. Math. 2011,51(1):81–98.
Bin Dehaish BA, Khamsi MA, Kozlowski WM: Common fixed points for asymptotic pointwise Lipschitzian semigroups inmodular function spaces.Fixed Point Theory Appl. 2013., 2013: Article ID 214
Bin Dehaish BA, Kozlowski WM: Fixed point iterations processes for asymptotic pointwise nonexpansivemappings in modular function spaces.Fixed Point Theory Appl. 2012., 2012: Article ID 118
Kozlowski WM Series of Monographs and Textbooks in Pure and Applied Mathematics122. In Modular Function Spaces. Dekker, New York; 1988.
Khamsi MA, Kozlowski WM, Reich S: Fixed point theory in modular function spaces.Nonlinear Anal. 1990, 14:935–953. 10.1016/0362-546X(90)90111-S
Khamsi MA, Kozlowski WM, Shutao C: Some geometrical properties and fixed point theorems in Orlicz spaces.J. Math. Anal. Appl. 1991,155(2):393–412. 10.1016/0022-247X(91)90009-O
Khamsi MA: Nonlinear semigroups in modular function spaces.Math. Jpn. 1992,37(2):1–9.
Khamsi MA: Fixed point theory in modular function spaces.Proceedings of the Workshop on Recent Advances on Metric Fixed PointTheory 1996, 31–57. (Seville, September 1995)
Dominguez-Benavides T, Khamsi MA, Samadi S: Uniformly Lipschitzian mappings in modular function spaces.Nonlinear Anal. 2001, 46:267–278. 10.1016/S0362-546X(00)00117-6
Dominguez-Benavides T, Khamsi MA, Samadi S: Asymptotically regular mappings in modular function spaces.Sci. Math. Jpn. 2001, 53:295–304.
Dominguez-Benavides T, Khamsi MA, Samadi S: Asymptotically nonexpansive mappings in modular function spaces.J. Math. Anal. Appl. 2002,265(2):249–263. 10.1006/jmaa.2000.7275
Hajji A, Hanebaly E: Perturbed integral equations in modular function spaces.Electron. J. Qual. Theory Differ. Equ. 2003., 2003: Article ID 20. http://www.math.u-szeged.hu/ejqtde/
Khamsi MA, Kozlowski WM: On asymptotic pointwise contractions in modular function spaces.Nonlinear Anal. 2010, 73:2957–2967. 10.1016/j.na.2010.06.061
Kozlowski WM: Advancements in fixed point theory in modular function.Arab. J. Math. 2012. 10.1007/s40065-012-0051-0
Kozlowski WM: An introduction to fixed point theory in modular function spaces. In Topics in Fixed Point Theory. Edited by: Almezel S, Ansari QH, Khamsi MA. Springer, Cham; 2014.
Kozlowski WM: On nonlinear differential equations in generalized Musielak-Orlicz spaces.Comment. Math. 2013,53(2):113–133.
Kozlowski WM: On the Cauchy problem for the nonlinear differential equations with values inmodular function spaces. In Proceeding of International Conference in Differential Geometry, FunctionalAnalysis and Applications. Narosa Publicactions, New Delhi; 2014. (8–10 September 2012, Jamia Millia Islamia University, New Delhi,India)
Bose SC: Weak convergence to the fixed point of an asymptotically nonexpansive.Proc. Am. Math. Soc. 1978, 68:305–308. 10.1090/S0002-9939-1978-0493543-4
Samanta SK: Fixed point theorems in a Banach space satisfying Opial’s condition.J. Indian Math. Soc. 1981, 45:251–258.
Passty GB: Construction of fixed points for asymptotically nonexpansive mappings.Proc. Am. Math. Soc. 1982, 84:212–216. 10.1090/S0002-9939-1982-0637171-7
Gornicki J: Weak convergence theorems for asymptotically nonexpansive mappings inuniformly convex Banach spaces.Comment. Math. Univ. Carol. 1989, 30:249–252.
Schu J: Iterative construction of fixed points of asymptotically nonexpansivemappings.J. Math. Anal. Appl. 1991, 158:407–413. 10.1016/0022-247X(91)90245-U
Schu J: Weak and strong convergence to fixed points of asymptotically nonexpansivemappings.Bull. Aust. Math. Soc. 1991, 43:153–159. 10.1017/S0004972700028884
Tan K-K, Xu H-K: The nonlinear ergodic theorem for asymptotically nonexpansive mappings inBanach spaces.Proc. Am. Math. Soc. 1992, 114:399–404. 10.1090/S0002-9939-1992-1068133-2
Xu H-K: Existence and convergence for fixed points of asymptotically nonexpansivetype.Nonlinear Anal. 1991, 16:1139–1146. 10.1016/0362-546X(91)90201-B
Tan K-K, Xu H-K: A nonlinear ergodic theorem for asymptotically nonexpansive mappings.Bull. Aust. Math. Soc. 1992, 45:25–36. 10.1017/S0004972700036972
Tan K-K, Xu H-K: Approximating fixed points of nonexpansive mappings by the Ishikawa iterationprocess.J. Math. Anal. Appl. 1993, 178:301–308. 10.1006/jmaa.1993.1309
Bruck R, Kuczumow T, Reich S: Convergence of iterates of asymptotically nonexpansive mappings in Banachspaces with the uniform Opial property.Colloq. Math. 1993,65(2):169–179.
Tan K-K, Xu H-K: Fixed point iteration processes for asymptotically nonexpansive mappings.Proc. Am. Math. Soc. 1994, 122:733–739. 10.1090/S0002-9939-1994-1203993-5
Rhoades BE: Fixed point iterations for certain nonlinear mappings.J. Math. Anal. Appl. 1994, 183:118–120. 10.1006/jmaa.1994.1135
Noor MA, Xu B: Fixed point iterations for asymptotically nonexpansive mappings in Banachspaces.J. Math. Anal. Appl. 2002, 267:444–453. 10.1006/jmaa.2001.7649
Khamsi MA: On asymptotically nonexpansive mappings in hyperconvex metric spaces.Proc. Am. Math. Soc. 2004, 132:365–373. 10.1090/S0002-9939-03-07172-7
Fukhar-ud-din H, Khan AR: Approximating common fixed points of asymptotically nonexpansive maps inuniformly convex Banach spaces.Comput. Math. Appl. 2009, 53:1349–1360.
Nanjaras B, Panyanak B:Demiclosed principle for asymptotically nonexpansive mappings in
 spaces.Fixed Point Theory Appl. 2010., 2010: Article ID 268780
spaces.Fixed Point Theory Appl. 2010., 2010: Article ID 268780Kozlowski WM: Fixed point iteration processes for asymptotic pointwise nonexpansivemappings in Banach spaces.J. Math. Anal. Appl. 2011,377(1):43–52. 10.1016/j.jmaa.2010.10.026
Kozlowski WM: Common fixed points for semigroups of pointwise Lipschitzian mappings inBanach spaces.Bull. Aust. Math. Soc. 2011, 84:353–361. 10.1017/S0004972711002668
Kozlowski WM, Sims B: On the convergence of iteration processes for semigroups of nonlinearmappings in Banach spaces. Springer Proceedings in Mathematics and Statistics 50. In Computational and Analytical Mathematics: In Honor of JonathanBorwein’s 60th Birthday. Edited by: Bailey DH, Bauschke HH, Borwein P, Garvan F, Thera M, Vanderwerff JD,Wolkowicz H. Springer, New York; 2013.
Kozlowski WM: On the construction of common fixed points for semigroups of nonlinearmappings in uniformly convex and uniformly smooth Banach spaces.Comment. Math. 2012,52(2):113–136.
Kozlowski WM: Notes on modular function spaces I.Comment. Math. 1988, 28:91–104.
Kozlowski WM: Notes on modular function spaces II.Comment. Math. 1988, 28:105–120.
Chen S: Geometry of Orlicz spaces.Diss. Math. 1996, 356:1–204.
Kaminska A: On uniform convexity of Orlicz spaces.Indag. Math. 1982,44(1):27–36.
Khamsi MA: A convexity property in modular function spaces.Math. Jpn. 1996,44(2):269–279.
Stewart I, Tall D: Algebraic Number Theory and Fermat’s Last Theorem. 3rd edition. AK Peters, Natick; 2001.
Acknowledgements
This work was funded by the Deanship of Scientific Research (DSR), King AbdulazizUniversity, Jeddah, under Grant No. (247-001-D1434). The authors,therefore, acknowledge with thanks technical and financial support of DSR.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally to the writing of this paper. All authors read andapproved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Bin Dehaish, B.A., Khamsi, M.A. & Kozlowski, W.M. On the convergence of iteration processes for semigroups of nonlinear mappings inmodular function spaces. Fixed Point Theory Appl 2015, 3 (2015). https://doi.org/10.1186/1687-1812-2015-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2015-3
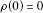 ;
; for all
for all 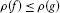 , where
, where 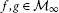 ;
;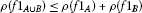 for any
for any 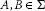 such that
such that 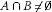 ,
, 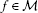 ;
;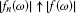 for all
for all 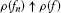 , where
, where  ;
; and
and  implies
implies  .
. is ρ-convergent to f and write
is ρ-convergent to f and write 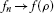 if and only if
if and only if 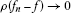 .
.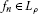 , is called ρ-Cauchy if
, is called ρ-Cauchy if 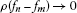 as
as  .
.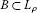 is called ρ-closed if for any sequence of
is called ρ-closed if for any sequence of 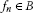 , the convergence
, the convergence 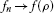 implies that f belongs to B.
implies that f belongs to B. .
.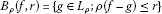 areρ-closed.
areρ-closed.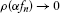 for an
for an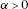 then there exists a subsequence
then there exists a subsequence of
of ρ-a.e.
ρ-a.e. whenever
whenever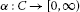 such that
such that 
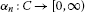 such that
such that 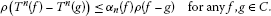
 for
for 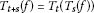 for
for  ;
; ,
, 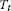 is an asymptotic pointwise nonexpansive mapping, i.e. there exists a function
is an asymptotic pointwise nonexpansive mapping, i.e. there exists a function 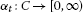 such that
such that 
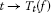 is ρ-continuous.
is ρ-continuous.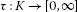 is called a ρ-type (or shortly a type) if there exists a one-parameter family
is called a ρ-type (or shortly a type) if there exists a one-parameter family  of elements of K such that for any
of elements of K such that for any 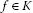 we have
we have 
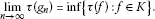
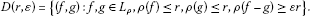
 , for every
, for every  , and
, and 
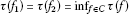 , then
, then .
.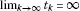 ,
,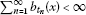 for every
for every 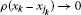 as
as , where
, where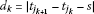 .
.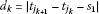 ,
,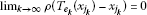 , where
, where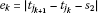 .
. spaces.Fixed Point Theory Appl. 2010., 2010: Article ID 268780
spaces.Fixed Point Theory Appl. 2010., 2010: Article ID 268780