- Research
- Open access
- Published:
On new fixed point results for  -contractive multi-valued mappings onα-complete metric spaces and their consequences
-contractive multi-valued mappings onα-complete metric spaces and their consequences
Fixed Point Theory and Applications volume 2015, Article number: 2 (2015)
Abstract
The purpose of this paper is to establish new fixed point results formulti-valued mappings satisfying an  -contractive condition, and viaBianchini-Grandolfi gauge functions, on α-complete metric spaces.Our results unify, generalize, and complement various results from theliterature. We also give examples which support our main result while previousresults in the literature are not applicable. Some of the fixed point results inmetric spaces endowed with an arbitrary binary relation and endowed with a graphare given here to illustrate the usability of the obtained results.
-contractive condition, and viaBianchini-Grandolfi gauge functions, on α-complete metric spaces.Our results unify, generalize, and complement various results from theliterature. We also give examples which support our main result while previousresults in the literature are not applicable. Some of the fixed point results inmetric spaces endowed with an arbitrary binary relation and endowed with a graphare given here to illustrate the usability of the obtained results.
MSC: 47H10, 54H25.
1 Introduction and preliminaries
Throughout this paper, we denote by ℕ,  , and ℝ the sets of positive integers,non-negative real numbers, and real numbers, respectively.
, and ℝ the sets of positive integers,non-negative real numbers, and real numbers, respectively.
We recollect some essential notations, required definitions, and primary resultscoherent with the literature. For a nonempty set X, we denote by the class of all nonempty subsets of X. Let
the class of all nonempty subsets of X. Let be a metric space, we denote by
be a metric space, we denote by the class of all nonempty closed subsets ofX, by
the class of all nonempty closed subsets ofX, by  the class of all nonempty closed bounded subsets ofX. For
the class of all nonempty closed bounded subsets ofX. For  , let the functional
, let the functional  be defined by
be defined by

for every  , where
, where  is the distance from a to
is the distance from a to . Such a functional is called the generalizedPompeiu-Hausdorff metric induced by d.
. Such a functional is called the generalizedPompeiu-Hausdorff metric induced by d.
In this paper, we denote by Ψ the class of functions  satisfying the following conditions:
satisfying the following conditions:
( ) ψ is a nondecreasing function;
) ψ is a nondecreasing function;
( )
)  , for all
, for all 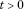 , where
, where  is the nth iterate of ψ.
is the nth iterate of ψ.
These functions are known in the literature as Bianchini-Grandolfi gauge functions insome sources (see e.g.[1–3]).
Remark 1.1 For each  , we see that the following assertions hold:
, we see that the following assertions hold:
-
1.
 , for all
, for all 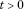 .
. -
2.
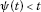 for each
for each 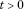 ;
; -
3.
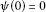 ;
;
Example 1.2 The function  defined by
defined by  , where
, where  , is a Bianchini-Grandolfi gauge function.
, is a Bianchini-Grandolfi gauge function.
Example 1.3 The function  defined by
defined by

is a Bianchini-Grandolfi gauge function.
In [4], Samet et al. introduced the concepts of anα-admissible mapping and anα-ψ-contractive mapping as follows.
Definition 1.4 ([4])
Let T be a self mapping on a nonempty set X and be a mapping. We say that T isα-admissible if the following condition holds:
be a mapping. We say that T isα-admissible if the following condition holds:

Definition 1.5 ([4])
Let  be a metric space and
be a metric space and  be a given mapping. We say that T is anα-ψ-contractive mapping if there exist two functions
be a given mapping. We say that T is anα-ψ-contractive mapping if there exist two functions and
and  such that
such that

for all  .
.
One also proved some fixed point theorems for such mappings on complete metric spacesand showed that these results can be utilized to derive fixed point theorems inpartially ordered metric spaces.
Afterwards, Asl et al.[5] introduced the concept of an 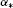 -admissible mapping which is a multi-valued version ofthe α-admissible mapping provided in [4].
-admissible mapping which is a multi-valued version ofthe α-admissible mapping provided in [4].
Definition 1.6 ([5])
Let X be a nonempty set,  and
and  be two mappings. We say that T is
be two mappings. We say that T is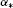 -admissible if the following condition holds:
-admissible if the following condition holds:

where  .
.
They extended the α-ψ-contractive condition of Sametet al.[4] from a single-valued version to a multi-valued version as follows.
Definition 1.7 ([5])
Let  be a metric space,
be a metric space,  be a multi-valued mapping and
be a multi-valued mapping and  be a given mapping. We say that T is anα-ψ-contractive multi-valued mapping if there exists
be a given mapping. We say that T is anα-ψ-contractive multi-valued mapping if there exists such that
such that

for all  .
.
Asl et al.[5] also established a fixed point result for multi-valued mappings oncomplete metric spaces satisfying an α-ψ-contractivecondition.
Recently, Ali et al.[6] introduced the notion of  -contractive multi-valued mappings, where
-contractive multi-valued mappings, where and Ξ is the family of functions
and Ξ is the family of functions satisfying the following conditions:
satisfying the following conditions:
( ) ξ is continuous;
) ξ is continuous;
( ) ξ is nondecreasing on
) ξ is nondecreasing on ;
;
( )
)  if and only if
if and only if  ;
;
( ) ξ is subadditive.
) ξ is subadditive.
Remark 1.8 From ( ) and (
) and ( ), we have
), we have  , for all
, for all  .
.
Example 1.9 Let  be a mapping which is defined by
be a mapping which is defined by

for each  , where
, where  is a Lebesgue integrable mapping which is summable oneach compact subset of
is a Lebesgue integrable mapping which is summable oneach compact subset of  and satisfies the following conditions:
and satisfies the following conditions:
-
for each
 , we have
, we have 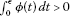 ;
; -
for each
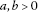 , we have
, we have 
Then  .
.
Lemma 1.10Let be a metric space. If
be a metric space. If , then
, then is a metric space.
is a metric space.
Lemma 1.11 ([6])
Let be a metric space,
be a metric space,  , and
, and . If there exists
. If there exists such that
such that , then there exists
, then there exists such that
such that

where .
.
Definition 1.12 ([6])
Let  be a metric space. A multi-valued mapping
be a metric space. A multi-valued mapping is called an
is called an  -contractive mapping if there exist three functions
-contractive mapping if there exist three functions ,
,  , and
, and  such that
such that

where  .
.
In the case when  is strictly increasing, the
is strictly increasing, the  -contractive mapping is called a strictly
-contractive mapping is called a strictly -contractive mapping.
-contractive mapping.
Ali et al.[6] also prove fixed point results for  -contractive multi-valued mapping on complete metricspaces.
-contractive multi-valued mapping on complete metricspaces.
Question 1 Is it possible to prove fixed point results for -contractive multi-valued mapping T undersome weaker condition for T?
-contractive multi-valued mapping T undersome weaker condition for T?
Question 2 Is it possible to prove fixed point results for -contractive multi-valued mapping in some space whichis more general than complete metric spaces?
-contractive multi-valued mapping in some space whichis more general than complete metric spaces?
Question 3 Is it possible to find some consequences or applications of thefixed point results?
On the other hand, Mohammadi et al.[7] extended the concept of an 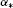 -admissible mapping to α-admissible asfollows.
-admissible mapping to α-admissible asfollows.
Definition 1.13 ([7])
Let X be a nonempty set,  and
and  be two given mappings. We say that T isα-admissible whenever for each
be two given mappings. We say that T isα-admissible whenever for each  and
and  with
with  , we have
, we have  , for all
, for all  .
.
Remark 1.14 It is clear that 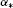 -admissible mapping is alsoα-admissible, but the converse may not be true as shown inExample 15 of [8].
-admissible mapping is alsoα-admissible, but the converse may not be true as shown inExample 15 of [8].
Recently, Hussain et al.[9] introduced the concept of α-completeness for metric spacewhich is a weaker than the concept of completeness.
Definition 1.15 ([9])
Let  be a metric space and
be a metric space and  be a mapping. The metric space X is said tobe α-complete if and only if every Cauchy sequence
be a mapping. The metric space X is said tobe α-complete if and only if every Cauchy sequence in X with
in X with  , for all
, for all  , converges in X.
, converges in X.
Remark 1.16 If X is complete metric space, then X is alsoα-complete metric space. But the converse is not true.
Example 1.17 Let  and the metric
and the metric  defined by
defined by  , for all
, for all  . Define
. Define  by
by

It is easy to see that  is not a complete metric space, but
is not a complete metric space, but is an α-complete metric space. Indeed,if
is an α-complete metric space. Indeed,if  is a Cauchy sequence in X such that
is a Cauchy sequence in X such that , for all
, for all  , then
, then  , for all
, for all  . Since
. Since  is a closed subset of ℝ, we see that
is a closed subset of ℝ, we see that is a complete metric space and then there exists
is a complete metric space and then there exists such that
such that  as
as  .
.
In this paper, we establish new fixed point results for  -contractive multi-valued mappings onα-complete metric spaces by using the idea ofα-admissible multi-valued mapping due to Mohammadi et al.[7]. These results are real generalization of main results of Ali etal.[6] and many results in literature. We furnish some interesting exampleswhich support our main theorems while results of Ali et al.[6] are not applicable. We also obtain fixed point results in metric spaceendowed with an arbitrary binary relation and fixed point results in metric spaceendowed with graph.
-contractive multi-valued mappings onα-complete metric spaces by using the idea ofα-admissible multi-valued mapping due to Mohammadi et al.[7]. These results are real generalization of main results of Ali etal.[6] and many results in literature. We furnish some interesting exampleswhich support our main theorems while results of Ali et al.[6] are not applicable. We also obtain fixed point results in metric spaceendowed with an arbitrary binary relation and fixed point results in metric spaceendowed with graph.
2 Main results
First, we introduce the concept of α-continuity for multi-valuedmappings in metric spaces.
Definition 2.1 Let  be a metric space,
be a metric space,  and
and  be two given mappings. We say T is anα-continuous multi-valued mapping on
be two given mappings. We say T is anα-continuous multi-valued mapping on  if, for all sequences
if, for all sequences  with
with  as
as  , and
, and  , for all
, for all  , we have
, we have  as
as  , that is,
, that is,

Note that the continuity of T implies the α-continuity ofT, for all mappings α. In general, the converse is nottrue (see in Example 2.2).
Example 2.2 Let  ,
,  and the metric
and the metric  defined by
defined by  , for all
, for all  . Define
. Define  and
and  by
by

and

Clearly, T is not a continuous multi-valued mapping on . Indeed, for sequence
. Indeed, for sequence  in X, we see that
in X, we see that  , but
, but  .
.
Next, we show that T is an α-continue multi-valued mapping on . Let
. Let  be a sequence in X such that
be a sequence in X such that as
as  and
and  , for all
, for all  . Then we have
. Then we have  , for all
, for all  . Therefore,
. Therefore,  . This shows that T is anα-continuous multi-valued mapping on
. This shows that T is anα-continuous multi-valued mapping on  .
.
Now we give first main result in this paper.
Theorem 2.3Let be a metric space and
be a metric space and be a strictly
be a strictly -contractive mapping. Suppose that thefollowing conditions hold:
-contractive mapping. Suppose that thefollowing conditions hold:
(S1)  is anα-complete metric space;
is anα-complete metric space;
(S2) Tis anα-admissible multi-valued mapping;
(S3) there exist and
and such that
such that ;
;
(S4) Tis anα-continuous multi-valued mapping.
ThenThas a fixed point.
Proof Starting from  and
and  in (S3), we have
in (S3), we have  . If
. If  , then we see that
, then we see that  is a fixed point of T. Assume that
is a fixed point of T. Assume that . If
. If  , we obtain that
, we obtain that  is a fixed point of T. Then we have nothingto prove. So we let
is a fixed point of T. Then we have nothingto prove. So we let  . From
. From  -contractive condition, we get
-contractive condition, we get

If  , then we get
, then we get

which is a contradiction. Therefore,  . From (2.1), we get
. From (2.1), we get

For fixed  by using Lemma 1.11, there exists
by using Lemma 1.11, there exists such that
such that

From (2.3) and (2.4), we have

Since ψ is strictly increasing function, we have

Put  and then
and then  .
.
If  or
or  , then we find that
, then we find that  is a fixed point of T and thus we havenothing to prove. Therefore, we may assume that
is a fixed point of T and thus we havenothing to prove. Therefore, we may assume that  and
and  . Since
. Since  ,
,  ,
,  , and T is an α-admissiblemulti-valued mapping, we have
, and T is an α-admissiblemulti-valued mapping, we have  . Applying from
. Applying from  -contractive condition, we have
-contractive condition, we have

Suppose that  . From (2.7), we get
. From (2.7), we get

which is a contradiction. Therefore, we may let  . From (2.7), we have
. From (2.7), we have

By using Lemma 1.11 with  , there exists
, there exists  such that
such that

From (2.9) and (2.10), we get

It follows from ψ being a strictly increasing function that

Continuing this process, we can construct a sequence  in X such that
in X such that  ,
,

and

for all  .
.
Let  such that
such that  . By the triangle inequality, we have
. By the triangle inequality, we have

Since  , we have
, we have  . Using
. Using  , we get
, we get  . This implies that
. This implies that  is a Cauchy sequence in
is a Cauchy sequence in  . From (2.13) and the α-completeness of
. From (2.13) and the α-completeness of , there exists
, there exists  such that
such that  as
as  .
.
By α-continuity of the multi-valued mapping T, we get

Now we obtain

Therefore,  and hence T has a fixed point. Thiscompletes the proof. □
and hence T has a fixed point. Thiscompletes the proof. □
Corollary 2.4Let be a metric space and
be a metric space and be a strictly
be a strictly -contractive mapping. Suppose that thefollowing conditions hold:
-contractive mapping. Suppose that thefollowing conditions hold:
(S1)  is anα-complete metric space;
is anα-complete metric space;
( ) Tis an
) Tis an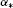 -admissible multi-valuedmapping;
-admissible multi-valuedmapping;
(S3) there exist and
and such that
such that ;
;
(S4) Tis anα-continuous multi-valued mapping.
ThenThas a fixed point.
Corollary 2.5 (Theorem 2.5 in [6])
Let be a complete metric space and
be a complete metric space and be a strictly
be a strictly -contractive mapping. Suppose that thefollowing conditions hold:
-contractive mapping. Suppose that thefollowing conditions hold:
(A1) Tis an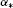 -admissible multi-valuedmapping;
-admissible multi-valuedmapping;
(A2) there exist and
and such that
such that ;
;
(A3) Tis a continuous multi-valued mapping.
ThenThas a fixed point.
Next, we give second main result in this work.
Theorem 2.6Let be a metric space and
be a metric space and be a strictly
be a strictly -contractive mapping. Suppose that thefollowing conditions hold:
-contractive mapping. Suppose that thefollowing conditions hold:
(S1)  is anα-complete metric space;
is anα-complete metric space;
(S2) Tis anα-admissible multi-valued mapping;
(S3) there exist and
and such that
such that ;
;
( ) if
) if is a sequence inXwith
is a sequence inXwith as
as and
and , for all
, for all , then we have
, then we have , for all
, for all .
.
ThenThas a fixed point.
Proof Following the proof of Theorem 2.3, we know that is a Cauchy sequence in X such that
is a Cauchy sequence in X such that as
as  and
and

for all  . From condition (
. From condition ( ), we get
), we get

for all  . By using the
. By using the  -contractive condition of T, we have
-contractive condition of T, we have

for all  . Suppose that
. Suppose that  . Let
. Let  . Since
. Since  as
as  , we can find
, we can find  such that
such that

for all  . Furthermore, we obtain that
. Furthermore, we obtain that

for all  . Also, as
. Also, as  is a Cauchy sequence, there exists
is a Cauchy sequence, there exists such that
such that

for all  . It follows from
. It follows from  as
as  that we can find
that we can find  such that
such that

for all  . Using (2.19)-(2.22), we get
. Using (2.19)-(2.22), we get

for all  . For
. For  , by (2.18) and the triangle inequality, we have
, by (2.18) and the triangle inequality, we have

Letting  in the above inequality, we get
in the above inequality, we get

This implies that  , which is a contradiction. Therefore,
, which is a contradiction. Therefore, , that is,
, that is,  . This completes the proof. □
. This completes the proof. □
Corollary 2.7Let be a metric space and
be a metric space and be a strictly
be a strictly -contractive mapping. Suppose that thefollowing conditions hold:
-contractive mapping. Suppose that thefollowing conditions hold:
(S1)  is anα-complete metric space;
is anα-complete metric space;
( ) Tis an
) Tis an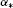 -admissible multi-valuedmapping;
-admissible multi-valuedmapping;
(S3) there exist and
and such that
such that ;
;
( ) if
) if is a sequence inXwith
is a sequence inXwith as
as and
and , for all
, for all , then we have
, then we have , for all
, for all .
.
ThenThas a fixed point.
Corollary 2.8 (Theorem 2.6 in [6])
Let be a complete metric space and
be a complete metric space and be a strictly
be a strictly -contractive mapping. Suppose that thefollowing conditions hold:
-contractive mapping. Suppose that thefollowing conditions hold:
(A1) Tis an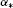 -admissible multi-valuedmapping;
-admissible multi-valuedmapping;
(A2) there exist and
and such that
such that ;
;
( ) if
) if is a sequence inXwith
is a sequence inXwith as
as and
and , for all
, for all , then we have
, then we have , for all
, for all .
.
ThenThas a fixed point.
Remark 2.9 Theorems 2.3 and 2.6 generalize many results in the followingsense:
-
The condition (1.1) is weaker than some kinds of the contractiveconditions such as Banach’s contractive condition [10], Kannan’s contractive condition [11], Chatterjea’s contractive condition [12], Nadler’s contractive condition [13], etc.;
-
the condition of being α-admissible of amulti-valued mapping T is weaker than the condition of being
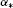 -admissible of T;
-admissible of T; -
for the existence of fixed point, we merely require thatα-continuity of T and α-completeness ofX, whereas other result demands stronger than these conditions.
Consequently, Theorems 2.3 and 2.6 extend and improve the following results:
-
Theorem 2.5 and Theorem 2.6 of Ali et al.[6];
-
Theorem 2.1 and Theorem 2.2 of Samet et al.[4];
-
Theorem 2.3 of Asl et al.[5];
-
Theorem 2.1 and Theorem 2.2 of Amiri et al.[14];
-
Theorem 2.1 of Salimi et al.[15];
-
Theorem 3.1 and Theorem 3.4 of Mohammadi et al.[7].
Next, we give an example to show that our result is more general than the results ofAli et al.[6] and many known results in the literature.
Example 2.10 Let  and the metric
and the metric  defined by
defined by  , for all
, for all  . Define
. Define  and
and  by
by

and

Clearly,  is not complete metric space. Therefore, the resultsof Ali et al.[6] are not applicable here.
is not complete metric space. Therefore, the resultsof Ali et al.[6] are not applicable here.
Next, we show that by Theorem 2.6 can be guaranteed the existence of a fixedpoint of T. Define functions  by
by  and
and  , for all
, for all  . It is easy to see that
. It is easy to see that  and
and  .
.
Firstly, we will show that T is a strictly  -contractive mapping. For
-contractive mapping. For  and
and  , we have
, we have  and then
and then

It is to be observed that ψ is strictly increasing function.Therefore, T is a strictly  -contractive mapping.
-contractive mapping.
Moreover, it is easy to see that T is an α-admissiblemulti-valued mapping and there exists  and
and  such that
such that

Also, T is an α-continuous mapping.
Finally, for each sequence  in X with
in X with  as
as  and
and  , for all
, for all  , we have
, we have  , for all
, for all  . Thus the condition (
. Thus the condition ( ) in Theorem 2.6 holds.
) in Theorem 2.6 holds.
Therefore, by using Theorem 2.3 or 2.6, we get T has a fixed point inX. In this case, T has infinitely fixed points such as−2, −1, and 0.
3 Consequences
3.1 Fixed point results in metric spaces endowed with an arbitrary binaryrelation
It has been pointed out in some studies that some results in metric spacesendowed with an arbitrary binary relation can be concluded from the fixed pointresults related with α-admissible mappings on metric spaces. Inthis section, we give some fixed point results on metric spaces endowed with anarbitrary binary relation which can be regarded as consequences of the resultspresented in the previous section. The following notions and definitions areneeded.
Let  be a metric space and ℛ be a binaryrelation over X. Denote
be a metric space and ℛ be a binaryrelation over X. Denote

i.e.,

Definition 3.1 Let X be a nonempty set and ℛ be a binaryrelation over X. A multi-valued mapping  is said to be a weakly comparative iffor each
is said to be a weakly comparative iffor each  and
and  with
with  , we have
, we have  , for all
, for all  .
.
Definition 3.2 Let  be a metric space and ℛ be a binaryrelation over X. The metric space X is said to be
be a metric space and ℛ be a binaryrelation over X. The metric space X is said to be -complete if and only if every Cauchy sequence
-complete if and only if every Cauchy sequence in X with
in X with  , for all
, for all  , converges in X.
, converges in X.
Definition 3.3 Let  be a metric space and ℛ be a binaryrelation over X. We say that
be a metric space and ℛ be a binaryrelation over X. We say that  is a
is a  -continuousmapping to
-continuousmapping to  if for given
if for given  and sequence
and sequence  with
with

Definition 3.4 Let  be a metric space and ℛ be a binaryrelation over X. A mapping
be a metric space and ℛ be a binaryrelation over X. A mapping  is called an
is called an  -contractive mapping if there exist two functions
-contractive mapping if there exist two functions and
and  such that
such that

where  .
.
In the case when  is strictly increasing, the
is strictly increasing, the -contractive mapping is called a strictly
-contractive mapping is called a strictly -contractive mapping.
-contractive mapping.
Theorem 3.5Let be a metric space, ℛ be a binary relation overXand
be a metric space, ℛ be a binary relation overXand be a strictly
be a strictly -contractive mapping. Suppose thatthe following conditions hold:
-contractive mapping. Suppose thatthe following conditions hold:
(S1)  is an
is an -complete metric space;
-complete metric space;
(S2) Tis a weakly comparative mapping;
(S3) there exist and
and such that
such that ;
;
(S4) Tis a -continuous multi-valued mapping.
-continuous multi-valued mapping.
ThenThas a fixed point.
Proof This result can be obtain from Theorem 2.3 by define amapping  by
by

This completes the proof. □
By using Theorem 2.6, we get the following result.
Theorem 3.6Let be a metric space, ℛ be a binary relation overXand
be a metric space, ℛ be a binary relation overXand be a strictly
be a strictly -contractive mapping. Suppose thatthe following conditions hold:
-contractive mapping. Suppose thatthe following conditions hold:
(S1)  is an
is an -complete metric space;
-complete metric space;
(S2) Tis a weakly comparative mapping;
(S3) there exist and
and such that
such that ;
;
( ) if
) if is a sequence inXwith
is a sequence inXwith as
as and
and , for all
, for all , then we have
, then we have , for all
, for all .
.
ThenThas a fixed point.
3.2 Fixed point results in metric spaces endowed with graph
In 2008, Jachymski [16] obtained a generalization of Banach’s contraction principle formappings on a metric space endowed with a graph. Afterwards, Dinevari and Frigon [17] extended some results of Jachymski [16] to multi-valued mappings. For more fixed point results on a metricspace with a graph, one can refer to [18–20].
In this section, we give fixed point results on a metric space endowed with agraph. Before presenting our results, we give the following notions anddefinitions.
Throughout this section, let  be a metric space. A set
be a metric space. A set  is called a diagonal of the Cartesian product
is called a diagonal of the Cartesian product and is denoted by Δ. Consider a graphG such that the set
and is denoted by Δ. Consider a graphG such that the set  of its vertices coincides with X and theset
of its vertices coincides with X and theset  of its edges contains all loops, i.e.,
of its edges contains all loops, i.e., . We assume G has no parallel edges, sowe can identify G with the pair
. We assume G has no parallel edges, sowe can identify G with the pair  . Moreover, we may treat G as a weightedgraph by assigning to each edge the distance between its vertices.
. Moreover, we may treat G as a weightedgraph by assigning to each edge the distance between its vertices.
Definition 3.7 Let X be a nonempty set endowed with a graphG and  be a multi-valued mapping, where X is anonempty set X. We say that Tweakly preserves edges if for each
be a multi-valued mapping, where X is anonempty set X. We say that Tweakly preserves edges if for each  and
and  with
with  , we have
, we have  , for all
, for all  .
.
Definition 3.8 Let  be a metric space endowed with a graphG. The metric space X is said to be
be a metric space endowed with a graphG. The metric space X is said to be  -complete if and only if every Cauchysequence
-complete if and only if every Cauchysequence  in X with
in X with  , for all
, for all  , converges in X.
, converges in X.
Definition 3.9 Let  be a metric space endowed with a graphG. We say that
be a metric space endowed with a graphG. We say that  is an
is an  -continuous mapping to
-continuous mapping to if for given
if for given  and sequence
and sequence  with
with

Definition 3.10 Let  be a metric space endowed with a graphG. A mapping
be a metric space endowed with a graphG. A mapping  is called an
is called an  -contractive mapping if there exist two functions
-contractive mapping if there exist two functions and
and  such that
such that

where  .
.
In the case when  is strictly increasing, the
is strictly increasing, the -contractive mapping is called a strictly
-contractive mapping is called a strictly -contractive mapping.
-contractive mapping.
Theorem 3.11Let be a metric space endowed with a graphG, and
be a metric space endowed with a graphG, and be a strictly
be a strictly -contractive mapping. Suppose thatthe following conditions hold:
-contractive mapping. Suppose thatthe following conditions hold:
(S1)  is an
is an -complete metric space;
-complete metric space;
(S2) Tweakly preserves edges;
(S3) there exist and
and such that
such that ;
;
(S4) Tis an -continuous multi-valuedmapping.
-continuous multi-valuedmapping.
ThenThas a fixed point.
Proof This result can be obtained from Theorem 2.3 by defining amapping  by
by

This completes the proof. □
By using Theorem 2.6, we get the following result.
Theorem 3.12Let be a metric space endowed with a graphGand
be a metric space endowed with a graphGand be a strictly
be a strictly -contractive mapping. Suppose thatthe following conditions hold:
-contractive mapping. Suppose thatthe following conditions hold:
(S1)  is an
is an -complete metric space;
-complete metric space;
(S2) Tweakly preserves edges;
(S3) there exist and
and such that
such that ;
;
( ) if
) if is a sequence inXwith
is a sequence inXwith as
as and
and , for all
, for all , then we have
, then we have for all
for all .
.
ThenThas a fixed point.
Remark 3.13
-
1.
If we assume G is such that
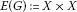 , then clearly G is connected and our Theorems 3.11 and 3.12 improve Nadler’s contraction principle [13] and in the case of a single-valued mapping, we improve Banach’s contraction principle [10], Kannan’s contraction theorem [11], Chatterjea’s contraction theorem [12], and Bianchini and Grandolfi’s fixed point theorem.
, then clearly G is connected and our Theorems 3.11 and 3.12 improve Nadler’s contraction principle [13] and in the case of a single-valued mapping, we improve Banach’s contraction principle [10], Kannan’s contraction theorem [11], Chatterjea’s contraction theorem [12], and Bianchini and Grandolfi’s fixed point theorem. -
2.
Theorems 3.11 and 3.12 are partial some generalized fixed point results endowed with a graph of Jachymski [16] and Dinevari and Frigon [17].
-
3.
Theorems 3.11 and 3.12 are generalizations of fixed point results of Theorem 2.5 and Theorem 2.6 of Ali et al. [6] in a graph version.
References
Bianchini RM, Grandolfi M: Trasformazioni di tipo contrattivo generalizzato in uno spazio metrico.Atti Accad. Naz. Lincei, Rend. Cl. Sci. Fis. Mat. Nat. 1968, 45:212–216.
Proinov PD: A generalization of the Banach contraction principle with high order ofconvergence of successive approximations.Nonlinear Anal. TMA 2007, 67:2361–2369. 10.1016/j.na.2006.09.008
Proinov PD: New general convergence theory for iterative processes and its applicationsto Newton-Kantorovich type theorems.J. Complex. 2010, 26:3–42. 10.1016/j.jco.2009.05.001
Samet B, Vetro C, Vetro P: Fixed-point theorems forα-ψ-contractive typemappings.Nonlinear Anal. 2012, 75:2154–2165. 10.1016/j.na.2011.10.014
Asl JH, Rezapour S, Shahzad N: On fixed points ofα-ψ-contractivemultifunctions.Fixed Point Theory Appl. 2012., 2012: Article ID 212
Ali MU, Kamran T, Karapinar E:
 -Contractive multivalued mappings.Fixed Point Theory Appl. 2014., 2014: Article ID 7
-Contractive multivalued mappings.Fixed Point Theory Appl. 2014., 2014: Article ID 7Mohammadi B, Rezapour S, Naseer S: Some results on fixed points ofα-ψ-Ciricgeneralized multifunctions.Fixed Point Theory Appl. 2013., 2013: Article ID 24
Minak G, Acar Ö, Altun I: Multivalued pseudo-Picard operators and fixed point results.J. Funct. Spaces Appl. 2013., 2013: Article ID 827458
Hussain N, Kutbi MA, Salimi P: Fixed point theory inα-complete metric spaces withapplications.Abstr. Appl. Anal. 2014., 2014: Article ID 280817
Banach S: Sur les opérations dans les ensembles abstraits et leur application auxéquations intégrales.Fundam. Math. 1922, 3:133–181.
Kannan R: Some results on fixed points. II.Am. Math. Mon. 1969, 76:405–408. 10.2307/2316437
Chatterjea SK: Fixed point theorems.C. R. Acad. Bulgare Sci. 1972, 25:727–730.
Nadler SB Jr.: Multi-valued contraction mappings.Pac. J. Math. 1969, 30:475–488. 10.2140/pjm.1969.30.475
Amiri P, Rezapour S, Shahzad N: Fixed points of generalizedα-ψ-contractions.Rev. R. Acad. Cienc. Exactas Fís. Nat., Ser. A Mat. 2014, 108:519–526. 10.1007/s13398-013-0123-9
Salimi P, Latif A, Hussain N: Modifiedα-ψ-contractive mappings withapplications.Fixed Point Theory Appl. 2013., 2013: Article ID 151
Jachymski J: The contraction principle for mappings on a metric space with a graph.Proc. Am. Math. Soc. 2008, 136:1359–1373.
Dinevari T, Frigon M: Fixed point results for multivalued contractions on a metric space with agraph.J. Math. Anal. Appl. 2013, 405:507–517. 10.1016/j.jmaa.2013.04.014
Beg I, Butt AR: Fixed point of set-valued graph contractive mappings.J. Inequal. Appl. 2013., 2013: Article ID 252
Chifu C, Petrusel G: Generalized contractions in metric spaces endowed with a graph.Fixed Point Theory Appl. 2012., 2012: Article ID 161
Nicolae A, O’Regan D, Petrusel A: Fixed point theorems for singlevalued and multivalued generalizedcontractions in metric spaces endowed with a graph.Georgian Math. J. 2011, 18:307–327.
Acknowledgements
The first author gratefully acknowledges the support from the Deanship ofScientific Research (DSR) at King Abdulaziz University (KAU) during thisresearch. The second author would like to thank the Thailand Research Fund andThammasat University under Grant No. TRG5780013 for financial supportduring the preparation of this manuscript.
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this paper. All authorsread and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Kutbi, M.A., Sintunavarat, W. On new fixed point results for  -contractive multi-valued mappings onα-complete metric spaces and their consequences.
Fixed Point Theory Appl 2015, 2 (2015). https://doi.org/10.1186/1687-1812-2015-2
-contractive multi-valued mappings onα-complete metric spaces and their consequences.
Fixed Point Theory Appl 2015, 2 (2015). https://doi.org/10.1186/1687-1812-2015-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2015-2
 , for all
, for all 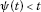 for each
for each 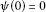 ;
; , we have
, we have 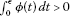 ;
;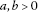 , we have
, we have 
 , then clearly G is connected and our Theorems 3.11 and 3.12 improve Nadler’s contraction principle [
, then clearly G is connected and our Theorems 3.11 and 3.12 improve Nadler’s contraction principle [