- Research
- Open access
- Published:
Coincidence point theorems in quasi-metric spaces without assuming the mixed monotone property and consequences in G-metric spaces
Fixed Point Theory and Applications volume 2014, Article number: 184 (2014)
Abstract
In this paper, we present some coincidence point theorems in the setting of quasi-metric spaces that can be applied to operators which not necessarily have the mixed monotone property. As a consequence, we particularize our results to the field of metric spaces, partially ordered metric spaces and G-metric spaces, obtaining some very recent results. Finally, we show how to use our main theorems to obtain coupled, tripled, quadrupled and multidimensional coincidence point results.
1 Introduction
In recent times, one of the branches of fixed point theory that has attracted much attention is the field devoted to studying this kind of results in the setting of partially ordered metric spaces. After the appearance of the first works in this sense (by Ran and Reurings [1], by Nieto and Rodríguez-López [2], by Gnana-Bhaskar and Lakshmikantham [3], and by Lakshmikantham and Ćirić [4], to cite some of them), the literature on this topic has expanded significantly. In [3], the authors introduced the notion of mixed monotone property, which has been one of the most usual hypotheses in this kind of results. However, some theorems avoiding these conditions have appeared very recently (see, for instance, [5]). One of the results on this line of study was given by Charoensawan and Thangthong in [6]. To understand their statement, the following notions were considered.
Definition 1.1 Let be a metric space and and be given mappings. Let M be a nonempty subset of . We say that M is an -invariant subset of if and only if for all ,
-
1.
;
-
2.
.
Definition 1.2 Let be a metric space and M be a subset of . We say that M satisfies the transitive property if and only if for all ,
Definition 1.3 Let Φ be the family of all functions satisfying
-
1.
,
-
2.
for all ,
-
3.
for all .
Using the previous preliminaries, they proved the following result in the context of G-metric spaces, which is recalled in Section 2.1.
Theorem 1.1 (Charoensawan and Thangthong [6], Theorem 3.1)
Let be a partially ordered set and G be a G-metric on X such that is a complete G-metric space, and let M be a nonempty subset of . Assume that there exists and also suppose that and such that
for all .
Suppose also that F is continuous, and g is continuous and commutes with F. If there exist such that
and M is an -invariant set which satisfies the transitive property, then there exist such that and .
First of all, notice that the partial order ≼ in the hypothesis has no sense in the statement of Theorem 1.1. This is only a mistake that proves the special importance of partial orders in this class of results.
In this paper, we show that Theorem 1.1 can be easily deduced from a unidimensional version of the same result. In fact, we prove that the middle variables of are unnecessary. But the main aim of this work is to obtain some coincidence point theorems in the context of quasi-metric spaces that can be applied in several frameworks, including metric spaces and G-metric spaces. The hypotheses of our main results are very general, and they can be particularized in a variety of different contexts, unidimensional or multidimensional ones, even if the involved mappings do not have the mixed monotone property. Our results also extend and unify some recent theorems that can be found in [7]. As a consequence, we prove that many results in this field of study can be easily derived from our statements.
2 Preliminaries
For the sake of completeness, we collect in this section some basic definitions and well-known results in this field. Firstly, let ℕ and ℝ denote the sets of all positive integers and all real numbers, respectively. Furthermore, we let . If is a nonempty subset of ℝ, the Euclidean metric on A is for all . In the sequel, let X be a nonempty set. Given a natural number n, we use to denote the nth Cartesian power of X, that is, (n times).
From now on, let be a self-mapping (also called operator). For simplicity, we denote by Tx and by . In general, the iterates of a self-mapping T are the mappings defined by
Given a point , the Picard sequence of the operator T (based on x) is the sequence , which we will denote by .
The main aim of this manuscript is to show some sufficient conditions to ensure existence and uniqueness of the following kinds of points. A coincidence point of two mappings is a point such that . And a coupled coincidence point of two mappings and is a point such that and . If g is the identity mapping on X, then both kinds of points are called coupled fixed point of T and coupled fixed point of F, respectively.
A metric (or a distance function) on a nonempty set X is a mapping verifying the following conditions: for all ,
In such a case, the pair is called a metric space.
We say that two mappings are commuting if for all . We say that and are commuting if for all .
A binary relation on X is a nonempty subset ℛ of . For simplicity, we will write if , and we will say that ≼ is the binary relation. We will write when and , and we will write when . We will say that x and y are ≼-comparable if or .
A binary relation ≼ on X is transitive if for all such that and . A preorder (or a quasi-order) ≼ on X is a binary relation on X that is reflexive (i.e., for all ) and transitive. In such a case, we say that is a preordered space (or a preordered set). If a preorder ≼ is also antisymmetric ( and implies ), then ≼ is called a partial order, and is a partially ordered space.
If is a preordered space and are two mappings, we say that T is a -nondecreasing mapping if for all such that . If g is the identity mapping on X, T is nondecreasing w.r.t. ≼ (or it is ≼-nondecreasing).
If is a metric space, a mapping is continuous if for all sequences such that . If ≼ is a binary relation on X, we say that T is -nondecreasing-continuous if for all sequences such that verifying that for all . If g is the identity mapping on X, we say that T is ≼-nondecreasing-continuous.
2.1 G-metric spaces
The notion of G-metric space is defined as follows.
Definition 2.1 (Mustafa and Sims [8])
Let X be a nonempty set, and let be a function satisfying the following properties:
(G1) if ;
(G2) for all with ;
(G3) for all with ;
(G4) (symmetry in all three variables);
(G5) (rectangle inequality) for all .
Then the function G is called a generalized metric, or, more specifically, a G-metric on X, and the pair is called a G-metric space.
Note that every G-metric on X induces a metric on X defined by
For a better understanding of the subject, we give the following examples of G-metrics.
Example 2.1 Let be a metric space. The function , defined by
for all , is a G-metric on X.
Example 2.2 (see, e.g., [8])
Let . The function , defined by
for all , is a G-metric on X.
In their initial paper, Mustafa and Sims [8] also defined the basic topological concepts in G-metric spaces as follows.
Definition 2.2 (Mustafa and Sims [8])
Let be a G-metric space, and let be a sequence of points of X. We say that is G-convergent to if
that is, for any , there exists such that for all . We call x the limit of the sequence, and we write or .
It is clear that the limit of a convergent sequence is unique.
Proposition 2.1 (Mustafa and Sims [8])
In a G-metric space , the following conditions are equivalent.
-
1.
is G-convergent to x.
-
2.
as .
-
3.
as .
Definition 2.3 (Mustafa and Sims [8])
Let be a G-metric space. A sequence is called a G-Cauchy sequence if, for any , there exists such that for all , that is, as .
Proposition 2.2 (Mustafa and Sims [8])
In a G-metric space , the following conditions are equivalent.
-
1.
The sequence is G-Cauchy.
-
2.
For any , there exists such that for all .
Definition 2.4 (Mustafa and Sims [8])
A G-metric space is called G-complete if every G-Cauchy sequence is G-convergent in .
Definition 2.5 Let be a G-metric space. A mapping is said to be G-continuous if G-converges to Tx for any G-convergent sequence to . In general, given , a mapping is said to be G-continuous if G-converges to for any G-convergent sequences such that for all .
The following lemma shows a simple way to consider some G-metrics on from a G-metric on X.
Lemma 2.1 (Agarwal et al. [9])
Let and be three mappings verifying
Then the following conditions are equivalent.
-
(a)
G is a -metric on X.
-
(b)
is a -metric on .
-
(c)
is a -metric on .
In such a case, the following properties hold.
-
1.
Every sequence verifies: .
-
2.
is -Cauchy ⟺ is -Cauchy ⟺ .
-
3.
is G-complete ⟺ is G-complete ⟺ is G-complete.
2.2 Quasi-metric spaces
Definition 2.6 A mapping is a quasi-metric on X if it satisfies (M1), (M2) and (M4), that is, if it verifies, for all :
(q1) if and only if ,
(q2) .
In such a case, the pair is called a quasi-metric space.
Remark 2.1 Any metric space is a quasi-metric space, but the converse is not true in general.
Now, we recollect some basic topological notions and related results about quasi-metric spaces (see also, e.g., [10–13]).
Definition 2.7 Let be a quasi-metric space, be a sequence in X, and . We will say that:
-
converges to x (and we will denote it by or by ) if ;
-
is a Cauchy sequence if for all , there exists such that for all .
The quasi-metric space is said to be complete if every Cauchy sequence is convergent on .
As q is not necessarily symmetric, some authors distinguished between left/right Cauchy/convergent sequences and completeness.
Definition 2.8 (Jleli and Samet [14])
Let be a quasi-metric space, be a sequence in X, and . We say that:
-
right-converges to x if ;
-
left-converges to x if ;
-
is a right-Cauchy sequence if for all there exists such that for all ;
-
is a left-Cauchy sequence if for all there exists such that for all ;
-
is right-complete if every right-Cauchy sequence is right-convergent;
-
is left-complete if every left-Cauchy sequence is left-convergent;
Remark 2.2 (see, e.g., [14])
A sequence in a quasi-metric space is Cauchy if and only if it is left-Cauchy and right-Cauchy.
Remark 2.3
-
1.
The limit of a sequence in a quasi-metric space, if it exists, is unique. However, this is false if we consider right-limits or left-limits.
-
2.
If and in a quasi-metric space, then , that is, q is continuous in both arguments. It follows from
for all n. In particular, and for all .
-
3.
If , and , then . It follows from
-
4.
If a sequence has a right-limit x and a left-limit y, then , converges and it has an only limit (from the right and from the left). However, it is possible that a sequence has two different right-limits when it has no left-limit.
Example 2.3 Let X be a subset of ℝ containing and define, for all ,
Then is a quasi-metric space. Notice that but . Therefore, right-converges to 0 but it does not converge from the left.
The following result shows a simple way to consider quasi-metrics from G-metrics.
Lemma 2.2 (Agarwal et al. [9])
Let be a G-metric space, and let us define by
Then the following properties hold.
-
1.
and are quasi-metrics on X. Moreover,
(2) -
2.
In and in , a sequence is right-convergent (respectively, left-convergent) if and only if it is convergent. In such a case, its right-limit, its left-limit and its limit coincide.
-
3.
In and in , a sequence is right-Cauchy (respectively, left-Cauchy) if and only if it is Cauchy.
-
4.
In and in , every right-convergent (respectively, left-convergent) sequence has a unique right-limit (respectively, left-limit).
-
5.
If and , then .
-
6.
If , then is G-Cauchy ⟺ is -Cauchy ⟺ is -Cauchy.
-
7.
is complete ⟺ is complete ⟺ is complete.
2.3 Control functions
Functions in Φ (see Definition 1.3) verify the following properties.
Lemma 2.3 Let .
-
1.
for all .
-
2.
If is a sequence such that for all n, then .
-
3.
If are two sequences such that and for all n, then .
Proof (2) By item 1, for all n, so is a nonincreasing sequence of nonnegative real numbers. Then it is convergent. Let . We claim that . If , then is a sequence of numbers greater than L that converges to L. Hence,
which is a contradiction.
-
(3)
It follows from item 2 taking into account that for all n. □
Inspired by Boyd and Wong’s theorem [15], Mukherjea [16] introduced the following kind of control functions:
Functions in Ψ are more general than those in Φ. The following properties are very useful.
Lemma 2.4 Let be a mapping, and let be a sequence.
-
1.
If and for all m, then .
-
2.
Let be two sequences such that and for all n. Also assume that if , then . Hence .
Proof (1) It is the same proof of item 2 of Lemma 2.3.
(2) It follows from the fact that if , and if . In any case, for all n. □
Remark 2.4 The difference between items 2 and 3 of Lemma 2.3 and items 1 and 2 of Lemma 2.4 is important. If we assume that and for all m, then it is impossible to deduce that or in item 1 of the previous result. For instance, define if , and . Then and the sequence verifies for all m but it does not converge.
3 Coincidence point theorems on quasi-metric spaces without the mixed monotone property
In this section, we present some coincidence point theorems in the framework of quasi-metric spaces under very general conditions which can be extended to the coupled case and can be applied to mappings that have not necessarily the mixed monotone property.
3.1 Basic notions depending on a subset ℳ
Definition 3.1 (See Kutbi et al. [5])
We say that a nonempty subset ℳ of is:
-
reflexive if for all ;
-
antisymmetric if for all such that ;
-
transitive if for all such that .
Given two mappings , we say that ℳ is:
-
g-transitive if for all such that ;
-
g-closed if for all such that ;
-
-closed if for all such that ;
-
-compatible if for all such that and .
Clearly, every transitive subset is also g-transitive. Moreover, ℳ is g-closed if and only if it is -closed, where denotes the identity mapping on X. The following lemma shows a simple way to consider g-transitive, -closed sets.
Lemma 3.1 Given a binary relation ≼ on X, let us consider , and let be two mappings.
-
1.
If ≼ is a preorder on X, then is reflexive, transitive and g-transitive.
-
2.
If ≼ is a partial order on X, then is reflexive, transitive, antisymmetric and g-transitive.
-
3.
is g-closed if and only if g is ≼-nondecreasing.
-
4.
is -closed if and only if T is -nondecreasing.
-
5.
If ≼ is a partial order on X and is -closed, then is -compatible.
Proof First four properties are obvious. We prove the last one. Since T is -nondecreasing,
□
It is convenient to highlight that the notion of g-transitive, -closed, nonempty subset is more general than the idea of nondecreasing mapping on a preordered space (following the previous lemma), as we show in the following example.
Example 3.1 Let and let us define by and for all . Let ℳ be the subset
Then ℳ does not come from a preorder (or a partial order) on X because it is not reflexive (), nor transitive ( but ) nor antisymmetric ( but ). However, ℳ is g-transitive and -closed.
In the following definitions, we will use sequences such that for all with . In this sense, the following notions must be called ‘right-notions’ because the same concepts could also be introduced involving sequences such that for all with (in this case, they would be ‘left-notions’). Then we could talk about -right-Picard sequences, ℳ-right-continuity, -right-compatibility and right-regularity. However, we advice the reader that, in order not to complicate the notation, we will omit the term ‘right’.
Definition 3.2 Let be a quasi-metric space, let ℳ be a nonempty subset of , and let be a mapping. We say that T is ℳ-continuous if for all sequences such that and for all with .
Remark 3.1 Every continuous mapping from a quasi-metric space into itself is also ℳ-continuous, whatever the subset ℳ.
Definition 3.3 Let be two mappings, let be a sequence, and let ℳ be a nonempty subset of . We say that is a:
-
-Picard sequence if
(3) -
-Picard sequence if it is a -Picard sequence and
(4)
Lemma 3.2 Let be two mappings.
-
1.
If , then there exists a -Picard sequence based on each .
-
2.
If ℳ is a g-transitive, -closed, nonempty subset of , then every -Picard sequence such that is a -Picard sequence.
Proof (1) Let be arbitrary. Since , then there exists such that . Similarly, since , then there exists such that . Repeating this argument by induction, we may consider a -Picard sequence based on .
(2) Assume that is a -Picard sequence such that . Since and ℳ is -closed, then , which means that . By induction, it follows that for all . And using that ℳ is g-transitive, we deduce that
for all such that . □
The following definition extends some ideas that can be found in [17–19].
Definition 3.4 Let be a quasi-metric space, and let ℳ be a nonempty subset of . Two mappings are said to be -compatible if
provided that is a sequence in X such that for all and
Similarly, T and g are said to be -compatible if
provided that is a sequence in X such that for all and
Clearly, if T and g are commuting, then they are both -compatible or -compatible. The following notion also extends the regularity of an ordered metric space.
Definition 3.5 Let be a quasi-metric space, and let and be two nonempty subsets. We say that is regular (or A is -regular) if we have that for all n provided that is a q-convergent sequence on A, is its q-limit and for all .
3.2 Coincidence point theorems using -contractions of the first kind
Next, we present the kind of contractions we will use.
Definition 3.6 Let be a quasi-metric space, let be two mappings, and let be a nonempty subset of . We say that T is a -contraction of the first kind if there exist such that
for all such that . If , we say that T is a -contraction of the first kind.
Remark 3.2 It is not necessary that functions in Φ and in Ψ verify all their properties in . In fact, as we shall only use inequalities (5)-(6), the properties of functions in Φ and in Ψ must only be verified on the image of the quasi-metric q, that is, on , which does not necessarily coincide with (for instance, if X is q-bounded).
Remark 3.3 One of the best advantages of using a subset is that a unique condition covers two particularly interesting cases:
-
, in which contractivity conditions (5)-(6) hold for all ; and
-
, where ≼ is a preorder or a partial order on X, in which (5)-(6) must be assumed for all such that .
Both possibilities were independently studied in the past, but this new vision unifies them in an only assumption.
The following one is a first property of this kind of mappings.
Lemma 3.3 Let be a quasi-metric space, let be two mappings, and let be a g-closed, nonempty subset of such that is regular. Suppose that, at least, one of the following conditions holds.
-
1.
T is a -contraction of the first kind.
-
2.
T is a -contraction of the first kind and ℳ is -compatible.
Then T is ℳ-continuous at every point in which g is ℳ-continuous.
Proof Let be a sequence such that and for all with . Taking into account that g is ℳ-continuous at z, then . As ℳ is g-closed, then for all with . Furthermore, as is regular, then for all . Applying the contractivity conditions (5)-(6), we have that, for all n,
If , then item 3 of Lemma 2.3 guarantees that and , so q-converges to Tz. If and we additionally assume that ℳ is -compatible, we can use item 2 of Lemma 2.4 applied to the sequences and in order to deduce that (notice that if , then ) and similarly . □
The first main result of this work is the following one.
Theorem 3.1 Let be a quasi-metric space, let be two mappings, and let ℳ be a nonempty subset of . Suppose that the following conditions are fulfilled.
-
(A)
There exists a -Picard sequence on X.
-
(B)
T is a -contraction of the first kind.
Also assume that, at least, one of the following conditions holds.
-
(a)
X (or or ) is q-complete, T and g are ℳ-continuous and the pair is -compatible;
-
(b)
X (or or ) is q-complete and T and g are ℳ-continuous and commuting;
-
(c)
is complete and X (or ) is -regular;
-
(d)
is complete, is closed and X (or ) is -regular;
-
(e)
is complete, g is ℳ-continuous, ℳ is g-closed, the pair is -compatible and X is -regular.
Then T and g have, at least, a coincidence point.
Notice that, by Lemma 3.2, the previous result also holds if we replace condition (A) by one of the following stronger hypotheses:
() and ℳ is g-transitive and -closed.
() ℳ is g-transitive and -closed, and there exists a -Picard sequence such that .
And by Remark 3.1, the ℳ-continuity of the mappings can be replaced by continuity.
Proof Let be an arbitrary -Picard sequence on X, and let be such that (5)-(6) hold. If there exists some such that , then , so is a coincidence point of T and g, and the proof is finished. On the contrary, assume that for all . Therefore,
Step 1. We claim that . Taking into account (4), if we apply the contractivity condition (5) to and , we obtain that
By item 2 of Lemma 2.3, we have that . Similarly, using and and the contractivity condition (6), we could deduce that . Therefore, we have proved that
Step 2. We claim that is right-Cauchy in , that is, for all , there is such that for all . We reason by contradiction. If is not right-Cauchy, there exist and two subsequences and verifying that
Taking as the smallest integer, greater than , verifying this property, we can suppose that
Therefore , and taking limit as , it follows from (8) that
Notice that, for all k,
and
Joining both inequalities we deduce that, for all k,
Letting , it follows from (8) that
Next, let us apply the contractivity condition (5) to and , taking into account that, by (7), . We get that, for all ,
Since for all n, and , then
Letting in (11) and taking into account (10) and (12), it follows that
which is a contradiction. This contradiction ensures us that is right-Cauchy in , and Step 2 holds.
Similarly, using the contractivity condition (6), it can be proved that is left-Cauchy in , so we conclude that is a Cauchy sequence in . Now, we prove that T and g have a coincidence point distinguishing between cases (a)-(e).
Case (a): X (or or ) is q-complete, T and g are ℳ-continuous and the pair is -compatible. As is complete, there exists such that (notice that as , then this property also occurs if or is q-complete). As T and g are ℳ-continuous, it follows from (4) that and . Taking into account that the pair is -compatible, we deduce that
In such a case, using item 2 of Remark 2.3, we conclude that
(the other case is similar). Hence, u is a coincidence point of T and g.
Case (b): X (or or ) is q-complete and T and g are ℳ-continuous and commuting. It is obvious because (b) implies (a).
Case (c): is complete and X (or ) is -regular. As is a Cauchy sequence in the complete space , there is such that . Let be any point such that . In this case, . We are also going to show that , so we will conclude that (and v is a coincidence point of T and g).
Indeed, as is a convergent sequence in such that for all , and X (or ) is -regular, then for all n, where is the limit of . Applying the contractivity conditions (5)-(6),
By item 3 of Lemma 2.3, q-converges to Tv.
Case (d): is complete, is closed and X (or ) is -regular. It follows from the fact that a closed subset of a complete quasi-metric space is also complete. Then is complete and case (c) is applicable.
Case (e): is complete, g is ℳ-continuous, ℳ is g-closed, the pair is -compatible and X is -regular. As is complete, there exists such that . As for all m, we also have that . As g is ℳ-continuous and for all , then . Furthermore, as the pair is -compatible, then
By item 3 of Remark 2.3, as , the previous properties imply that . We are going to show that and this finishes the proof.
Indeed, since X is -regular, and for all , then for all n. Moreover, taking into account that ℳ is g-closed, then for all n. Applying the contractivity conditions (5)-(6),
As , then . □
Example 3.2 To illustrate the applicability of Theorem 3.1, we show the following example in which mappings are nonlinear. Let and let
Clearly, ℳ does not come from any partial order on X as in Lemma 3.1 because it is not antisymmetric: but . Let us consider on X the function given, for all , by
Then q is a complete quasi-metric on ℝ. In fact, it has the same convergent sequences to the same limits as the Euclidean metric for all because
However, q is not a metric because .
Now, given a real number , let us consider the mappings defined, for all , by
Also consider the function defined by for all . Clearly, . We are going to show that Theorem 3.1 is applicable to the previous setting, because the previous properties hold.
-
1.
The sequence , given by for all , is a -Picard sequence.
-
2.
The function is bijective and nondecreasing.
-
3.
The range of g, which is , is closed and complete in .
-
4.
We claim that T is a -contraction of the first kind. To prove it, let be such that . If , then (5)-(6) are obvious. Next, assume that . In particular, . Hence, because g is bijective. Therefore, the condition leads to two cases.
-
If , then . Therefore
-
If , then . In such a case,
-
5.
Let be a sequence such that for all . Then one, and only one, of the following cases holds.
(5.a) There exists such that . In this case, and for all .
To prove it, notice that is only possible when or . In any case, . Repeating this argument, for all . But if , the condition also leads to . And we can again repeat the argument.
(5.b) There exists such that . In this case, for all .
(5.c) There exists such that for all . In this case, is a constant sequence.
-
6.
The range is -regular. To prove it, let and let be a sequence such that and for all . In particular, using the Euclidean metric. We can distinguish the previous three cases.
(6.a) Suppose that and for all . Therefore, and for all , so for all .
(6.b) Suppose that for all . Then and, therefore, for all .
(6.c) Suppose that for all . Therefore and for all .
The previous properties show that case (c) of Theorem 3.1 is applicable, so T and g have, at least, a coincidence point, which is .
Notice that T and g do not satisfy the condition
because if and , then
We extend the previous theorem to the case in which .
Theorem 3.2 If we additionally assume that ℳ is -compatible, then Theorem 3.1 also holds even if T is a -contraction of the first kind.
Proof We can follow, point by point, the proof of the previous result and obtain inequalities (13)-(14). In this case, we cannot use Lemma 2.3, but we may use the fact that ℳ is -compatible. Therefore, we know that, as for all n, then
By item 2 of Lemma 2.4 we conclude that . In the same way, , so q-converges to Tv.
The same argument is valid when applied to inequalities (15)-(16). □
3.3 Coincidence point theorems using -contractions of the second kind
Many results on fixed point theory in the setting of G-metrics can be similarly proved using the quasi-metrics and associated to G as in Lemma 2.2 (see, for instance, Agarwal et al. [9]). These families of quasi-metrics verify additional properties that are not true for an arbitrary quasi-metric. Using these properties, it is possible to relax some conditions on the kind of considered contractions, obtaining similar results. This is the case of the following kind of mappings.
Definition 3.7 Let be a quasi-metric space, let be two mappings, and let be a nonempty subset of . We say that T is a -contraction of the second kind if there exists such that
for all such that . If , we say that T is a -contraction of the second kind.
Notice that condition (17) is not symmetric on x and y because does not imply . In order to compensate this absence of symmetry, we will suppose an additional condition on the ambient space.
Definition 3.8 We say that a quasi-metric space is:
-
right-Cauchy if every right-Cauchy sequence in is, in fact, a Cauchy sequence in ;
-
left-Cauchy if every left-Cauchy sequence in is, in fact, a Cauchy sequence in ;
-
right-convergent if every right-convergent sequence in is, in fact, a convergent sequence in ;
-
left-convergent if every left-convergent sequence in is, in fact, a convergent sequence in .
It is convenient not to confuse the previous notions with the concept of left/right complete quasi-metric space given in Definition 2.8. Lemma 2.2 guarantees that there exists a wide family of quasi-metrics that verify all the previous properties.
Corollary 3.1 Every quasi-metric and associated to a G-metric G on X is right and left-Cauchy and right and left-convergent.
Next we prove a similar result to Theorem 3.1. In this case, the contractivity condition is weaker but we suppose additional conditions on the ambient space.
Theorem 3.3 Let be a right-Cauchy quasi-metric space, let be two mappings, and let ℳ be a nonempty subset of . Suppose that the following conditions are fulfilled.
-
(A)
There exists a -Picard sequence on X.
-
(B)
T is a -contraction of the second kind.
Also assume that, at least, one of the following conditions holds.
-
(a)
X (or or ) is q-complete, T and g are ℳ-continuous and the pair is -compatible;
-
(b)
X (or or ) is q-complete and T and g are ℳ-continuous and commuting;
-
(c)
is complete and right-convergent, and X (or ) is -regular;
-
(d)
is complete and right-convergent, is closed and X (or ) is -regular;
-
(e)
is complete and right-convergent, g is ℳ-continuous, ℳ is g-closed, the pair is -compatible and X is -regular.
Then T and g have, at least, a coincidence point.
Notice that, by Lemma 3.2, the previous result also holds if we replace condition (A) by one of the following stronger hypotheses:
() and ℳ is g-transitive and -closed.
() ℳ is g-transitive and -closed, and there exists a -Picard sequence such that .
And by Remark 3.1, the ℳ-continuity of the mappings can be replaced by continuity.
Proof We can follow, step by step, the lines of the proof of Theorem 3.1 to deduce, in the case for all , that is right-Cauchy in . Using that is right-Cauchy, then it is a Cauchy sequence in . Now, we prove that T and g have a coincidence point distinguishing between cases (a)-(e). Cases (a) and (b) have the same proof as in Theorem 3.1.
Case (c): is complete and right-convergent, and X (or ) is -regular. As is a Cauchy sequence in the complete space , there is such that . Let be any point such that . In this case, . We are also going to show that , so we will conclude that (and v is a coincidence point of T and g).
Indeed, as is a convergent sequence in such that for all , and X (or ) is -regular, then for all n, where is the limit of . Applying the contractivity condition (17),
By item 3 of Lemma 2.3, we have that , which means that right-converges to Tv. Since is right-convergent, then is a convergent sequence in , and by item 4 of Remark 2.3, it converges to Tv.
Case (d): is complete and right-convergent, is closed and X (or ) is -regular. It follows from the fact that a closed subset of a complete quasi-metric space is also complete. Then is complete and case (c) is applicable.
Case (e): is complete and right-convergent, g is ℳ-continuous, ℳ is g-closed, the pair is -compatible and X is -regular. It follows step by step as in case (e) of the proof of Theorem 3.1 but, replacing (15)-(16) by the only inequality
In this case, by item 3 of Lemma 2.3, we have that , which means that right-converges to Tu. Since is right-convergent, then is a convergent sequence in , and by item 4 of Remark 2.3, it converges to Tu. □
Example 3.3 Theorem 3.3 can also be applied to mappings given in Example 3.2 because is right-convergent.
Repeating the arguments of Theorem 3.2, we extend the previous theorem to the case in which .
Theorem 3.4 If we additionally assume that ℳ is -compatible, then Theorem 3.3 also holds even if T is a -contraction of the second kind.
3.4 Consequences
The previous theorems admit a lot of different particular cases employing continuity, the condition and the case in which g is the identity mapping on X. We highlight the following one in which a partial order is involved. Preliminaries of the following result can be found in [20].
Corollary 3.2 (Al-Mezel et al. [20], Theorem 34)
Let be an ordered metric space, and let be two mappings such that the following properties are fulfilled.
-
(i)
;
-
(ii)
T is monotone -nondecreasing;
-
(iii)
there exists such that ;
-
(iv)
there exists verifying
Also assume that, at least, one of the following conditions holds.
-
(a)
is complete, T and g are continuous and the pair is O-compatible;
-
(b)
is complete and T and g are continuous and commuting;
-
(c)
is complete and is nondecreasing-regular;
-
(d)
is complete, is closed and is nondecreasing-regular;
-
(e)
is complete, g is continuous and monotone ≼-nondecreasing, the pair is O-compatible and is nondecreasing-regular.
Then T and g have, at least, a coincidence point.
Proof It is only necessary to apply Theorem 3.2 to the subset , taking into account the properties given in Lemma 3.1. Notice that in case (e), we use Lemma 3.3 to avoid assuming that T is continuous. □
The following result improves the last one because we do not assume that T is ℳ-continuous in hypothesis (b).
Corollary 3.3 Let be a complete quasi-metric space, let be two mappings such that , and let ℳ be a g-transitive, -closed, nonempty subset of . Suppose that T is a -contraction (respectively, T is a -contraction and ℳ is -compatible), g is ℳ-continuous, T and g are commuting and there exists such that . Also assume that, at least, one of the following conditions holds.
-
(a)
T is ℳ-continuous, or
-
(b)
ℳ is g-closed and is regular.
Then T and g have, at least, a coincidence point.
Proof We show that case (b) in Theorem 3.1 is applicable. By item 1 of Lemma 3.2, X contains a -Picard sequence based on , and by item 2 of the same lemma, is a -Picard sequence.
If T is ℳ-continuous, item (b) of Theorem 3.1 (and also Theorem 3.2 in the case of a -contraction) can be used to ensure that T and g have, at least, a coincidence point. In other case, if ℳ is g-closed and is regular, then Lemma 3.3 guarantees that T is ℳ-continuous. □
Another interesting particularization is the following one.
Corollary 3.4 (Karapınar et al. [7], Theorem 33)
Let be a complete metric space, let be two mappings such that , and let be a -compatible, -closed, transitive subset. Assume that there exists such that
Also assume that, at least, one of the following conditions holds.
-
(a)
T and g are M-continuous and -compatible;
-
(b)
T and g are continuous and commuting;
-
(c)
is regular and gX is closed.
If there exists a point such that , then T and g have, at least, a coincidence point.
As a consequence, in the following result, a partial order is not necessary.
Corollary 3.5 (Karapınar et al. [7], Corollary 35)
Let be a complete metric space, and let ≼ be a transitive relation on X. Let be two mappings such that and T is -nondecreasing. Suppose that there exists such that
Also suppose that
Assume that either
-
(a)
T and g are continuous and commuting, or
-
(b)
is regular and gX is closed.
If there exists a point such that , then T and g have, at least, a coincidence point.
4 Applications to G-metric spaces
One of the most interesting, recent lines of research in the field of fixed point theory is devoted to G-metric spaces. Taking into account Lemma 2.2, we can take advantage of our main results to present some new theorems in this area. The following result is an easy application to G-metric spaces.
Corollary 4.1 Let be a complete G-metric space, let be two mappings such that , and let be a g-transitive, -closed, nonempty subset of . Assume that T and g are continuous and commuting, and there exists such that
for all such that . If there exists such that , then T and g have, at least, a coincidence point.
Notice that this result is also valid if and ℳ is -compatible.
Proof It follows from Theorem 3.3 and Corollary 3.1 using the quasi-metric associated to G (as in Lemma 2.2). Notice that there exists a -Picard sequence on X by items 1 and 2 of Lemma 3.2. □
In order not to lose the power and usability of Theorems 3.3 and 3.4, we present the following properties comparing and .
Definition 4.1 Let be a G-metric space, and let and be two nonempty subsets. We say that is regular (or A is -regular) if we have that for all n provided that is a G-convergent sequence on A, is its G-limit and for all .
Lemma 4.1 Given a G-metric space and nonempty subsets and , the following conditions are equivalent:
-
1.
the subset A is -regular;
-
2.
the subset A is -regular;
-
3.
the subset A is -regular.
Proof It follows from the fact that , and have the same convergent sequences, and they converge to the same limits. □
Similarly, the following result can be proved.
Lemma 4.2 Given a G-metric space , a nonempty subset and two mappings , we have that the pair is -compatible (respectively, -compatible) in if and only if it is -compatible (respectively, -compatible) in .
Proof It follows from the fact that and have the same convergent sequences, and they converge to the same limits. Furthermore, taking into account that , then if and only if . □
Definition 4.2 Let be a G-metric space, and let ℳ be a nonempty subset of . Two mappings are said to be -compatible if the pair is -compatible in (or, equivalently, in ).
Similarly, the notion of -compatibility in a G -metric space can be defined. We present the following result, which is a complete version of our main results in the context of G-metric spaces.
Corollary 4.2 Let be a G-metric space, let be two mappings, and let ℳ be a nonempty subset of . Suppose that, at least, one of the following conditions holds.
-
(A)
There exists a -Picard sequence on X.
() and ℳ is g-transitive and -closed.
() ℳ is g-transitive and -closed, and there exists a -Picard sequence such that .
Also assume that, at least, one of the following two conditions holds.
(B) There exists such that
for all for which .
(B′) The subset ℳ is -compatible and there exists such that
for all for which .
Additionally, assume that, at least, one of the following eight conditions holds.
-
(a)
X (or or ) is G-complete, T and g are ℳ-continuous and the pair is -compatible;
(a′) X (or or ) is G-complete, T and g are continuous and the pair is -compatible;
-
(b)
X (or or ) is G-complete and T and g are ℳ-continuous and commuting;
(b′) X (or or ) is G-complete and T and g are continuous and commuting;
-
(c)
is complete and X (or ) is -regular;
-
(d)
is complete, is closed and X (or ) is -regular;
-
(e)
is complete, g is ℳ-continuous, ℳ is g-closed, the pair is -compatible and X is -regular.
(e′) is complete, g is continuous, ℳ is g-closed, the pair is -compatible and X is -regular.
Then T and g have, at least, a coincidence point.
Proof It follows from Theorems 3.3 and 3.4 taking into account Corollary 3.1, Lemmas 2.2, 4.2 and Definition 4.2. Notice that (A′) ⇒ () ⇒ (A), (a′) ⇒ (a), (b′) ⇒ (b) and (e′) ⇒ (e). □
We particularize the previous result to the case in which , associated to a preorder or a partial order ≼ on X. In such a case, Lemma 3.1 is applicable. We leave to the reader to interpret ≼-nondecreasing-continuity as -continuity, G-regularity as -compatibility, O-compatibility as -compatibility, and -compatibility as -compatibility.
Corollary 4.3 Let be a G-metric space provided with a preorder ≼, and let be two mappings such that and T is -nondecreasing. Assume that, at least, one of the following two conditions holds.
(B) There exists such that
for all for which .
(B′) ≼ is a partial order on X and there exists such that
for all for which .
Additionally, assume that, at least, one of the following eight conditions holds.
-
(a)
X (or or ) is G-complete, T and g are ≼-nondecreasing-continuous and the pair is -compatible;
(a′) X (or or ) is G-complete, T and g are continuous and the pair is -compatible;
-
(b)
X (or or ) is G-complete and T and g are ≼–nondecreasing-continuous and commuting;
(b′) X (or or ) is G-complete and T and g are continuous and commuting;
-
(c)
is complete and X (or ) is G-regular;
-
(d)
is complete, is closed and X (or ) is G-regular;
-
(e)
is complete, g is ≼-nondecreasing and ≼-nondecreasing-continuous, the pair is O-compatible and X is G-regular.
(e′) is complete, g is ≼-nondecreasing and continuous, the pair is O-compatible and X is G-regular.
If there exists verifying , then T and g have, at least, a coincidence point.
We also leave to the reader the task of particularizing the previous results to the case in which g is the identity mapping on X, obtaining fixed points of T.
5 Coupled coincidence point theorems
In this section, we deduce that Theorem 1.1 follows from Theorem 3.3. However, the main aim of this subsection is to describe how Theorems 3.1, 3.2, 3.3 and 3.4 can be employed in order to obtain some coupled coincidence point theorems, because these techniques can be extrapolated to many contexts.
We introduce the following notation. Given two mappings and , we define , for all , by
Lemma 5.1 Let and be two mappings.
-
1.
If , then .
-
2.
If F and g are commuting, then and
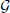 are also commuting.
are also commuting. -
3.
A point is a coincidence point of and
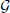 if and only if it is a coincidence point of F and g.
if and only if it is a coincidence point of F and g.
Proof (2) It follows from
for all . □
5.1 Charoensawan and Thangthong’s coupled coincidence point result in G-metric spaces
One of the key objectives of this subsection is to prove that, in Theorem 1.1, the middle variables of M are not necessary. Indeed, given a nonempty subset , let us define
Notice that is a subset of .
Lemma 5.2 Let and be two mappings, and let .
-
1.
If there exist such that
then . In particular, is nonempty.
-
2.
If M is transitive, then is transitive and
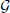 -transitive.
-transitive. -
3.
If M verifies the second property of Definition 1.1, then is a -closed set.
-
4.
If M is an -invariant set, then is a -closed set.
We point out that we will only use the second property of the notion of -invariant set (Definition 1.1). This shows that -closed sets are more general than an -invariant set because the first property will not be employed (this was also established in Kutbi et al. [5]).
Proof (1) By definition, implies that , which means that .
(2) Assume that M is transitive, and let be such that . Therefore
As M is transitive, then , so . Therefore, is transitive, and it is also 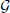 -transitive because every transitive subset is also
-transitive because every transitive subset is also 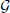 -transitive, whatever
-transitive, whatever 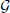 .
.
-
(3)
Assume that M is an -invariant set, and let be such that . By definition, since , then . As M is -invariant, then
In particular, , which means that . Hence, is a -closed set. □
In the following result, we use the quasi-metric on associated, by Lemma 2.2, to the G-metric given by
that is, for all ,
Using this notation, the following result is obvious.
Lemma 5.3 Let be a G-metric space, and let M be a nonempty subset of such that is nonempty. Let and be two mappings such that there exists verifying
for all . Then
for all such that .
Notice that condition (21) is weaker than condition (1). The previous properties prove the following consequence.
Lemma 5.4 Let be a G-metric space, and let and be two mappings.
-
1.
If F is G-continuous, then is -continuous.
-
2.
If g is G-continuous, then
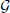 is -continuous.
is -continuous.
Proof It is a straightforward exercise. □
Corollary 5.1 Theorem 1.1 follows from Theorem 3.3.
Proof Under the hypothesis of Theorem 1.1, let us consider the quasi-metric space , the mappings and 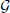 and the subset defined by (20). By item 3 of Lemma 2.1, is a complete G-metric space, and by item 7 of Lemma 2.2, is a complete quasi-metric space. Furthermore, Corollary 3.1 guarantees that is left/right-Cauchy and left/right-convergent. Lemma 5.4 ensures that and
and the subset defined by (20). By item 3 of Lemma 2.1, is a complete G-metric space, and by item 7 of Lemma 2.2, is a complete quasi-metric space. Furthermore, Corollary 3.1 guarantees that is left/right-Cauchy and left/right-convergent. Lemma 5.4 ensures that and 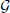 are -continuous. Lemma 5.2 proves that and is a transitive, -closed, nonempty subset of . Finally, Lemma 5.3 ensures that is a -contraction of the second kind. As a consequence, case (b) of Theorem 3.3 (replacing condition (A) by (A′), and ℳ-continuity by continuity) guarantees that and
are -continuous. Lemma 5.2 proves that and is a transitive, -closed, nonempty subset of . Finally, Lemma 5.3 ensures that is a -contraction of the second kind. As a consequence, case (b) of Theorem 3.3 (replacing condition (A) by (A′), and ℳ-continuity by continuity) guarantees that and 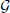 have, at least, a coincidence point, which is a coincidence point of F and g. □
have, at least, a coincidence point, which is a coincidence point of F and g. □
In fact, the previous proof shows that two conditions are not necessary in Theorem 3.3: neither the first property of -invariant sets nor the middle variables of M in .
5.2 Kutbi et al.’s coupled fixed point theorems without the mixed monotone property
In [5], the authors introduced the following notion and proved the following result.
Definition 5.1 (Kutbi et al. [5])
Let be a mapping, and let M be a nonempty subset of . We say that M is an F-closed subset of if, for all ,
Corollary 5.2 (Kutbi et al. [5], Theorem 16)
Let be a complete metric space, let be a continuous mapping, and let M be a subset of . Assume that:
-
(i)
M is F-closed;
-
(ii)
there exists such that ;
-
(iii)
there exists such that for all , we have
Then F has a coupled fixed point.
5.3 Sintunaravat et al.’s coupled fixed point theorems without the mixed monotone property
Similarly, the following result is a consequence of our main results.
Corollary 5.3 (Sintunaravat et al. [21])
Let be a complete metric space and M be a nonempty subset of . Assume that there is a function with and for each , and also suppose that is a mapping such that
for all . Suppose that either
-
(a)
F is continuous, or
-
(b)
for any two sequences , with ,
for all , then for all .
If there exists such that and M is an F-invariant set which satisfies the transitive property, then there exist such that and , that is, F has a coupled fixed point.
5.4 Choudhury and Kundu’s coupled coincidence point theorems under the mixed g-monotone property
Although our main results in Section 3 do not need the mixed monotone property, we show in this subsection how to interpret that property using a subset , so that our main results are also applicable to this context. We start recalling this notion.
Definition 5.2 Let ≼ be a binary relation on X, and let and be two mappings. We say that F has the mixed g-monotone property (with respect to ≼) if is monotone g-nondecreasing in x and monotone g-nonincreasing in y, that is, for any ,
The binary relation ≼ on X can be extended to as follows:
If ≼ is a partial order on X, then ⊑ is a partial order on . It is easy to show that if F has the mixed -monotone property, then is a -nondecreasing mapping and, by Lemma, is -closed.
Corollary 5.4 (Choudhury and Kundu [17], Theorem 3.1)
Let be a partially ordered set, and let there be a metric d on X such that is a complete metric space. Let be such that and for all . Let and be two mappings such that F has the mixed g-monotone property and satisfy
Let , g be continuous and monotone increasing and F and g be compatible mappings. Also suppose that
-
(a)
F is continuous, or
-
(b)
X has the following properties:
-
(i)
if a nondecreasing sequence , then for all ;
-
(ii)
if a nonincreasing sequence , then for all .
If there exist such that and , then there exist such that and , that is, F and g have a coupled coincidence point in X.
Proof It is only necessary to consider the metric on given by
and to use the previous properties in using and 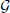 . □
. □
6 Conclusions
As conclusion, we highlight that coupled coincidence point theorems can be easily deduced from Theorems 3.1, 3.2, 3.3 and 3.4 applied to the quintuple . Exactly in the same way, tripled, quadrupled and multidimensional coincidence point results can be derived (following the arguments in [9, 20, 22–26]).
References
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proc. Am. Math. Soc. 2004, 132: 1435–1443. 10.1090/S0002-9939-03-07220-4
Nieto JJ, Rodríguez-López R: Contractive mapping theorem in partially ordered sets and applications to ordinary differential equations. Order 2005, 22: 223–239. 10.1007/s11083-005-9018-5
Gnana-Bhaskar T, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal. 2006, 65: 1379–1393. 10.1016/j.na.2005.10.017
Lakshmikantham V, Ćirić LJ: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Anal. 2009, 70(12):4341–4349. 10.1016/j.na.2008.09.020
Kutbi MA, Roldán A, Sintunavarat W, Martínez-Moreno J, Roldán C: F -Closed sets and coupled fixed point theorems without the mixed monotone property. Fixed Point Theory Appl. 2013., 2013: Article ID 330
Charoensawan P, Thangthong C: On coupled coincidence point theorems on partially ordered G -metric spaces without mixed g -monotone. J. Inequal. Appl. 2014., 2014: Article ID 150
Karapınar E, Roldán A, Shahzad N, Sintunavarat W: Discussion of coupled and tripled coincidence point theorems for ϕ -contractive mappings without the mixed g -monotone property. Fixed Point Theory Appl. 2014., 2014: Article ID 92
Mustafa Z, Sims B: A new approach to generalized metric spaces. J. Nonlinear Convex Anal. 2006, 7: 289–297.
Agarwal, R, Karapınar, E, Roldán, A: Fixed point theorems in quasi-metric spaces and applications to coupled/tripled fixed points on -metric spaces. J. Nonlinear Convex Anal. (to appear)
Al-Sulami HH, Karapınar E, Khojasteh F, Roldán A: A proposal to the study of contractions in quasi metric spaces. Discrete Dyn. Nat. Soc. 2014., 2014: Article ID 269286
Karapınar E, Lakzian H:-Contractive mappings on generalized quasi-metric spaces. J. Funct. Spaces 2014., 2014: Article ID 914398
Karapınar E, Romaguera S, Tirado P: Contractive multivalued maps in terms of Q -functions on complete quasimetric spaces. Fixed Point Theory Appl. 2014., 2014: Article ID 53
Bilgili N, Karapınar E, Samet B: Generalized α - ψ contractive mappings in quasi-metric spaces and related fixed point theorems. J. Inequal. Appl. 2014., 2014: Article ID 36
Jleli M, Samet B: Remarks on G -metric spaces and fixed point theorems. Fixed Point Theory Appl. 2012., 2012: Article ID 210
Boyd DW, Wong JSW: On nonlinear contractions. Proc. Am. Math. Soc. 1969, 20: 458–464. 10.1090/S0002-9939-1969-0239559-9
Mukherjea A: Contractions and completely continuous mappings. Nonlinear Anal. 1997, 1(3):235–247.
Choudhury BS, Kundu A: A coupled coincidence point result in partially ordered metric spaces for compatible mappings. Nonlinear Anal. 2010, 73: 2524–2531. 10.1016/j.na.2010.06.025
Luong NV, Thuan NX: Coupled points in ordered generalized metric spaces and application to integro-differential equations. Comput. Math. Appl. 2011, 62(11):4238–4248. 10.1016/j.camwa.2011.10.011
Hung NM, Karapınar E, Luong NV: Coupled coincidence point theorem for O -compatible mappings via implicit relation. Abstr. Appl. Anal. 2012., 2012: Article ID 796964
Al-Mezel SA, Alsulami HH, Karapınar E, Roldán A: Discussion on ‘Multidimensional coincidence points’ via recent publications. Abstr. Appl. Anal. 2014., 2014: Article ID 287492
Sintunavarat W, Kumam P, Cho Y-J: Coupled fixed point theorems for nonlinear contractions without mixed monotone property. Fixed Point Theory Appl. 2012., 2012: Article ID 170
Karapınar E, Roldán A, Martínez-Moreno J, Roldán C: Meir-Keeler type multidimensional fixed point theorems in partially ordered metric spaces. Abstr. Appl. Anal. 2013., 2013: Article ID 406026
Roldán A, Karapınar E:Some multidimensional fixed point theorems on partially preordered-metric spaces under -contractivity conditions. Fixed Point Theory Appl. 2013., 2013: Article ID 158
Roldán A, Martínez-Moreno J, Roldán C: Multidimensional fixed point theorems in partially ordered complete metric spaces. J. Math. Anal. Appl. 2012, 396(2):536–545. 10.1016/j.jmaa.2012.06.049
Roldán A, Martínez-Moreno J, Roldán C, Karapınar E:Multidimensional fixed point theorems in partially ordered complete partial metric spaces under-contractivity conditions. Abstr. Appl. Anal. 2013., 2013: Article ID 634371
Roldán A, Karapınar E, Kumam P: G -Metric spaces in any number of arguments and related fixed-point theorems. Fixed Point Theory Appl. 2014., 2014: Article ID 13
Acknowledgements
The authors thank anonymous referees for their remarkable comments, suggestions and ideas that helped to improve this paper. M de la Sen is grateful to the Spanish Government for its support of this research through Grant DPI2012-30651 and to the Basque Government for its support of this research through Grants IT378-10 and SAIOTEK S-PE12UN015. He is also grateful to the University of Basque Country for its financial support through Grant UFI 2011/07. A-F Roldán-López-de-Hierro has been partially supported by Junta de Andalucía by project FQM-268 of the Andalusian CICYE.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Roldán-López-de-Hierro, AF., Karapınar, E. & de la Sen, M. Coincidence point theorems in quasi-metric spaces without assuming the mixed monotone property and consequences in G-metric spaces. Fixed Point Theory Appl 2014, 184 (2014). https://doi.org/10.1186/1687-1812-2014-184
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2014-184