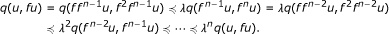Fixed point results under c-distance in tvs-cone metric spaces

Abstract

Fixed point and common fixed point results for mappings in tvs-cone metric spaces (with the underlying cone which is not normal) under contractive conditions expressed in the terms of c-distance are obtained. Respective results concerning mappings without periodic points are also deduced. Examples are given to distinguish these results from the known ones.

Mathematics Subject Classification (2010)

47H10, 54H25

1 Introduction

Cone metric spaces were considered by Huang and Zhang in [1], who reintroduced the concept which has been known since the middle of 20th century (see, e.g., [2–4]). Topological vector space-valued version of these spaces was treated in [5–13]; see also [14] for a survey of fixed point results in these spaces.

Fixed point theorems in metric spaces with the so-called w-distance were obtained for the first time by Kada et al. in [15] where nonconvex minimization problems were treated. Further results were given, e.g., in [16–18]. Cone metric version of this notion (usually called a c-distance) was used, e.g., in [19, 20].

In this paper, we consider fixed point and common fixed point results for mappings in tvs-cone metric spaces (with the underlying cone which is not normal) under contractive conditions expressed in the terms of c-distance. Respective results concerning mappings without periodic points are also deduced. Examples are given to distinguish these results from the known ones.

2 Preliminaries

Let E be a real Hausdorff topological vector space (tvs for short) with the zero vector θ. A proper nonempty and closed subset P of E is called a cone if P + P ⊂ P, λP ⊂ P for λ ≥ 0 and P ∩ (-P) = {θ}. We shall always assume that the cone P has a nonempty interior int P (such cones are called solid).

Each cone P induces a partial order ≼ on E by x ≼ y ⇔ y - × ∈ P. x π y will stand for (x ≼ y and x ≠ y), while x ≪ y will stand for y - × ∈ int P. The pair (E, P) is an ordered topological vector space.

For a pair of elements x, y in E such that x ≼ y, put [x, y] = {z ∈ E : x ≼ z ≼ y}. A subset A of E is said to be order-convex if [x, y] ⊂ A, whenever x, y ∈ A and x ≼ y.

Ordered topological vector space (E, P) is order-convex if it has a base of neighborhoods of θ consisting of order-convex subsets. In this case, the cone P is said to be normal. If E is a normed space, this condition means that the unit ball is order-convex, which is equivalent to the condition that there is a number k such that x, y ∈ E and 0 ≼ x ≼ y implies that ||x|| ≤ k||y||. A proof of the following assertion can be found, e.g., in [2].

Theorem 1 If the underlying cone of an ordered tvs is solid and normal, then such tvs must be an ordered normed space.

Note that completions of cone metric spaces in the case of nonnormal underlying cone were treated in [21].

From [1, 5–7], we give the following

Definition 1 Let X be a nonempty set and (E, P) an ordered tvs. A function d : X × X → E is called a tvs-cone metric and (X, d) is called a tvs-cone metric space if the following conditions hold:

(c1) θ ≼ d(x, y) for all x, y ∈ X and d(x, y) = θ if and only if x = y;

(c2) d(x, y) = d(y, x) for all x, y ∈ X;

(c3) d(x, z) ≼ d(x, y) + d(y, z) for all x, y, z ∈ X.

Taking into account Theorem 1, proper generalizations when passing from norm-valued cone metric spaces of [1] to tvs-cone metric spaces can be obtained only in the case of nonnormal cones. We shall make use of the following properties:

(p₁) If u, v, w ∈ E, u ≼ v and v ≪ w then u ≪ w.

(p₂) If u ∈ E and θ ≼ u ≪ c for each c ∈ int P then u = θ.

(p₃) If u _n , v _n , u, v ∈ E, θ ≼ u _n ≼ v _n for each n ∈ ℕ, and u _n → u, v _n → v (n → ∞), then θ ≼ u ≼ v.

(p₄) If x _n , x ∈ X, u _n ∈ E, d(x _n , x) ≼ u _n and u _n → θ (n → ∞), then x _n → x (n → ∞).

(p₅) If u ≼ λu, where u ∈ P and 0 ≤ λ < 1, then u = θ.

(p₆) If c ≫ θ and u _n ∈ E, u _n → θ (n → ∞), then there exists n₀ such that u _n ≪ c for all n ≥ n₀.

In the sequel, E will always denote a topological vector space, with the zero vector θ and with order relation ≼, generated by a solid cone P. For notions such as convergent and Cauchy sequences, completeness, continuity etc. in (tvs)-cone metric spaces, we refer to [1, 7, 14] and references therein.

Kada et al. [15] introduced the notion of w-distance in metric spaces and proved some fixed point results using this notion (see also [16–18]). Cho et al. [19] transferred it to the setting of cone metric spaces (see also [20]).

Definition 2[19] Let (X, d) be a tvs-cone metric space. A function q : X × X → E is called a c-distance in X if:

(q1) θ ≼ q(x, y) for all x, y ∈ X;

(q2) q(x, z) ≼ q(x, y) + q(y, z) for all x, y, z ∈ X;

(q3) If a sequence {y _n } in X converges to a point y ∈ X, and for some x ∈ X and u = u _x ∈ P, q(x, y _n ) ≼ u holds for each n ∈ ℕ, then q(x, y) ≼ u;

(q4) For each c ∈ E with θ ≪ c, there exists e ∈ E with θ ≼ e, such that q(z, x) ≪ e and q(z, y) ≪ e implies d(x, y) ≪ c.

Each w-distance q in a metric space (X, d) (in the sense of [15]) is a c-distance in the tvs-cone metric space (X, d) (with E = ℝ and P = [0, +∞)). Indeed, only property (q3) has to be checked. Let y _n ∈ X, y _n → y in the cone metric d (n → ∞), and let q(x, y _n ) ≤ u _x ∈ [0, +∞). Since q is (as a w-distance) lower semi-continuous, we have that q(x, y) ≤ lim inf_{n → ∞}q(x, y _n ) ≤ lim inf_{n → ∞}u _x = u _x , i.e., q(x, y) ≤ u _x holds true.

The first two of the following examples are variations of [[19], Examples 2.7, 2.8], adjusted to the case of a tvs-cone metric.

Example 1 Let (X, d) be a tvs-cone metric space such that the metric d(·,·) is a continuous function in second variable. Then, q(x, y) = d(x, y) is a c-distance. Indeed, only property (q3) is nontrivial and it follows from q(x, y _n ) = d(x, y _n ) ≼ u, passing to the limit when n → ∞ and using continuity of d.

Example 2 Let (X, d) be a tvs-cone metric space, and let u ∈ X be fixed. Then, q(x, y) = d(u, y) defines a c-distance on X. Indeed, (q1) and (q3) are clear. (q2) follows from q(x, z) = d(u, z) ≼ d(u, y) + d(u, z) = q(x, y) + q(y, z). Finally, (q4) is obtained by taking e = c/ 2.

Example 3 Consider the Banach space E = C[0, 1] of real-valued continuous functions with the max-norm and ordered by the cone P = {f ∈ E : f(t) ≥ 0 for t ∈ [0, 1]}. This cone is normal in the Banach-space topology on E. Let τ* be the strongest locally convex topology on the vector space E. Then, the cone P is solid, but it is not normal in the topology τ*. Indeed, if this were the case, Theorem 1 would imply that the topology τ* is normed, which is impossible since an infinite dimensional space with the strongest locally convex topology cannot be metrizable (see, e.g., [14]).

Let now X = [0, + ∞) and d : X × X → (E, τ*) be defined by d(x, y)(t) = |x - y|φ(t) for a fixed element φ ∈ P. Then, (X, d) is a tvs-cone metric space which is not a cone metric space in the sense of [1]. We can introduce two c-distances on this space:

They are the examples of c-distances in tvs-cone metric spaces which are not c-distances in cone metric spaces of [19, 20].

These examples show, among other things, that for a c-distance q:

• 1. q(x, y) = q(y, x) does not necessarily hold for all x, y ∈ X;

• 2. q(x, y) = θ is not necessarily equivalent to x = y.

3 Results

3.1 Fixed point and common fixed point results under c-distance

We will call a sequence {u _n } in P a c-sequence if for each c ≫ θ there exists n₀ ∈ N such that u _n ≪ c for n ≥ n₀. It is easy to show that if {u _n } and {v _n } are c-sequences in E and α, β > 0, then { αu _n + βv _n } is a c-sequence.

Note that in the case that the cone P is normal, a sequence in E is a c-sequence iff it is a θ -sequence (see property (p₆)). However, when the cone is not normal, a c-sequence need not be a θ -sequence (see [7, 14]). Also, from [7], we know that the cone metric d need not be a continuous function.

The following lemma is a tvs-cone metric version of lemmas from [15, 19].

Lemma 1 Let (X, d) be a tvs-cone metric space and let q be a c-distance on X. Let {x _n } and {y _n } be sequences in × and x, y, z ∈ X. Suppose that {u _n } and {v _n } are c-sequences in P. Then the following hold:

(1) If q(x _n , y) ≼ u _n and q(x _n , z) ≼ v _n for n ∈ ℕ, then y = z. In particular, if q(x, y) = θ and q(x, z) = θ, then y = z.

(2) If q(x _n , y _n ) ≼ u _n and q(x _n , z) ≼ v _n for n ∈ ℕ, then {y _n } converges to z.

(3) If q(x _n , x _m ) ≼ u _n for m > n > n₀, then {x _n } is a Cauchy sequence in X.

(4) If q(y, x _n ) ≼ u _n for n ∈ ℕ, then {x _n } is a Cauchy sequence in X.

Proof We will prove assertions (1) and (2). Proofs of the other two are similar.

• (1) In order to prove that y = z, according to (p₂), it is enough to show that d(y, z) ≪ c for each c ≫ θ. For the given c choose e ≫ θ such that property (q4) is satisfied. Choose then n ₀ ∈ ℕ such that u _n ≪ e and v _n ≪ e for n ≥ n ₀. Then, by property (p₁), we get that q(x _n , y) ≪ e and q(x _n , z) ≪ e and (q4) imply that d(y, z) ≪ c.

• (2) Let again c ≪ θ be arbitrary and choose a corresponding e ≫ θ satisfying property (q4). If n ₀ ∈ N is such that u _n ≪ e and v _n ≪ e for n ≥ n ₀, then (p₁) implies that q(x _n , y _n ) ≪ e and q(x _n , z) ≪ e for n ≥ n ₀. Then, by (q4), d(y _n , z) ≪ c and y _n → z (n → ∞). ■

Our first result is the following theorem of Hardy-Rogers type.

Theorem 2 Let (X, d) be a complete tvs-cone metric space and let q be a c-distance on X. Suppose that a continuous self-map f : X → X satisfies the following two conditions:

(3.1)

(3.2)

for all x, y ∈ X, where A, B, C, D, E are nonnegative constants such that A + B + C + 2D + 2E < 1. Then f has a fixed point in X. If fu = u, then q(u, u) = θ.

Proof Let x₀ ∈ X be arbitrary and form the sequence {x _n } with x _n = fⁿx₀. In order to prove that it is a Cauchy sequence, put x = x _n and y = x_{n - 1}in (3.1) to get

(3.3)

Similarly, putting y = x_{n - 1}and x = x _n in (3.2), one obtains

(3.4)

Denote u _n = q(x_n+1, x _n )+ q(x _n , x_n+1). Adding up (3.3) and (3.4), we get that

i.e. u _n ≼ hu_{n - 1}with

since A + B + C + 2D + 2E < 1 and, e.g., A + C + E > 0.

By induction, u _n ≼ hⁿu₀ and q(x _n , x_n+1) ≼ u _n ≼ hⁿ (q(x₁, x₀) + q(x₀, x₁)). In the usual way, it follows that

for m > n, where {v _n } is a c-sequence. Lemma 1.(3) implies that {x _n } is a Cauchy sequence in X and, since X is complete, x _n → x* ∈ X (n → ∞). Continuity of f implies that x_n+1= fx _n → fx*, and since the limit of a sequence in tvs-cone metric space in unique, we get that fx* = x*.

Suppose that fu = u. Then, (3.1) implies that

which is, by property (p₅) and A + B + C + D + E < A + B + C +2D +2E < 1, possible only if q(u, u) = θ. ■

Some special cases of the previous theorem, for example Banach-type and Kannan-type fixed point results, need only one condition:

and

respectively.

Remark 1 If the underlying cone P of the given tvs-cone metric space (X, d) is normal (and, hence, this space is a cone metric space in the sense of [1], see Theorem 2.1), then continuity of f in Theorem 2 can be replaced by the condition

It may be of interest to note that in this case, property (q3) of c-distance has to be used in the course of the proof (see, e.g., the respective procedure in ordered cone metric spaces in [19]), while in our case (when f is continuous), this property is not needed.

The next is a result including two mappings and the existence of their common fixed point.

Theorem 3 Let (X, d) be a complete tvs-cone metric space and let q be a c-distance on X. Suppose that continuous self-maps f, g : X → X satisfy the following two conditions:

(3.5)

(3.6)

for all x, y ∈ X, where A, B, D are nonnegative constants, such that A + 2B + 4D < 1. Then f and g have a common fixed point in X. If fu = gu = u, then q(u, u) = θ.

Proof Let x₀ ∈ X be arbitrary and form the sequence {x _n } such that x_2n+1= fx_2nand x_2n+2= gx_2n+1for n ≥ 0. Denote u _n = q(x_2n, x_2n+1)+q(x_2n+1, x_2n) and v _n = q(x_2n+1, x_2n+2) + q(x_2n+2, x_2n+1).

Putting x = x_2n+2, y = x_2n+1in (3.5) we obtain that

(3.7)

Similarly, putting the same values for x, y in (3.6), we get

(3.8)

It follows by adding up (3.7) and (3.8) that

i.e.,

where , since A + B + D > 0 and A + 2B + 4D < 1.

By a similar procedure, starting with x = x_2nand y = x_2n+1, one can get

Combining the last two inequalities, it follows that

and we get that {u _n } and {v _n } are c-sequences. We have that q(x_2n, x_2n+1) ≼ u _n , q(x_2n+1, x_2n+2) ≼ v _n and it follows that q(x _n , x_n+1) ≼ u _n + v _n , where u _n + v _n is a c-sequence. Using Lemma 1.(3), we obtain that {x _n } is a Cauchy sequence in X. Hence, x _n → x* ∈ X (n → ∞). Since f and g are continuous, it easily follows from the definition of {x _n } that fx* = gx* = x*.

Thus, mappings f and g have a common fixed point. Suppose that u ∈ X is any point satisfying fu = gu = u. Then, (3.5) implies that

and, since 0 < A + 2B + 2D < A + 2B + 4D < 1, property (p₅) implies that q(u, u) = θ. ■

As corollaries, we obtain, for example, common fixed point result for self-maps f and g satisfying

(3.9)

or for a self-map f satisfying

where m, n ∈ ℕ, A + 2B + 4D < 1.

Remark 2 Similarly as in Remark 1, we note that if the cone P is normal, then continuity of mappings f and g in Theorem 3 can be replaced by conditions

Example 4 Let E = ℝ and P = [0, +∞). Let X = [0, +∞), d(x, y) = |x - y| and define q(x, y) = x. It is easy to check that q is a c-distance on a cone metric space (X, d).

Take functions f, g : X → X defined by and . If x = 5, , then and . Hence, there is no A ∈ (0, 1) (and hence no triple (A, B, D)) such that d(fx, gy) ≤ Ad(x, y) for each x, y ∈ [0, +∞), i.e., the existence of a common fixed point of f and g cannot be deduced from the well-known metric version of Theorem 3.

However, conditions of the c-distance version (Theorem 3) are satisfied. Indeed, take arbitrary A, and B = D = 0. Then, for each x, y ∈ [0, +∞), and (see (3.9)). Note that f and g have a (trivial) common fixed point u = 0 and that q(u, u) = q(0, 0) = 0.

This example can be easily modified to the tvs-cone metric case. It is enough to define tvs-cone metric on X by d(x, y)(t) = |x - y|φ(t) with fixed φ ∈ P = {f ∈ C[0, 1] : f(t) ≥ 0 for t ∈ [0, 1]} and take c-distance q₁(x, y)(t) = x · φ (t) (see Example 3).

3.2 Mappings without periodic points

The first part of the following result was given with an incorrect proof in [20] (using lim inf which may not be defined in the case of an arbitrary cone metric space).

Recall that a map f : X → X is said to have property (P) if it satisfies F(f) = F(fⁿ ) for each n ∈ ℕ, where F(f) stands for the set of all fixed points of f[22].

Theorem 4 Let (X, d) be a tvs-cone metric space and q : X × X → E be a c-distance on X. Suppose that a continuous self-map f : X → X satisfies

(3.10)

for some λ ∈ (0, 1) and each × ∈ X. Then:

1. f has a fixed point and if fu = u, then q(u, u) = θ;

2. f has property (P).

Proof (1) Let x₀ ∈ X and x_n+1= fx _n , n ≥ 0. If for some n₀ ∈ ℕ₀, then is a fixed point of f. Otherwise, we get from (3.10) that

Using Lemma 1.(3) again, one obtains that {x _n } is a Cauchy sequence in X.

Hence, x _n → x*, and continuity of f implies that x_n+1= fx _n → fx* and fx* = x*.

• (2) Obviously, F(f) ⊆ F(fⁿ ) for each n ∈ ℕ. Let u ∈ F(fⁿ ), i.e., fⁿu = u. Then, (3.10) implies that

  

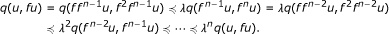
By property (p₅), it follows that q(u, fu) = θ.

Now, for arbitrary k ∈ {1, 2,..., n}, we have that q(f^ku, f^k+1u) ≼ λ^kq(u, fu) θ and so q(f^ku, f^k+1u) = θ. It follows that q(u, f²u) ≼ q(u, fu)+q(fu, f²u) = θ, i.e., q(u, f²u) = θ and, similarly,

From q(u, fu) = θ = q(u, fⁿu) = q(u, u) and Lemma 1.(1), we conclude that fu = u, i.e., u ∈ F(f). ■

Another way to obtain property (P) is the following.

Theorem 5 Let (X, d) be a tvs-cone metric space and q : X × X → E be a c-distance on X. Suppose that a continuous self-map f : X → X satisfies

(3.11)

for some λ ∈ (0, 1) and each × ∈ X. Then f has property (P).

Proof Denote z₁(x) = q(x, fx)+ q(fx, x) and z₂(x) = q(fx, f²x)+ q(f²x, fx).

Then, the given condition is written as z₂(x) ≼ λz₁(x) for each x ∈ X. Suppose that fⁿu = u. Then,

Since 0 < λⁿ < 1, property (p₅) implies that z₁(u) = q(u, fu) + q(fu, u) = θ. Again, the triangle inequality (q2) implies that q(u, u) = q(fu, fu) = θ, and by Lemma 1.(1), we get that fu = u. ■

Corollary 1 Let q be a c-distance on a tvs-cone metric space (X, d) and let f : X → X be continuous and such that for some nonnegative A, B, C, D, E such that A + B + C + 2D + 2E < 1, inequalities (3.1) and (3.2) hold for all x, y ∈ X. Then f has property (P).

Proof Putting x = x and y = fx in conditions (3.1) and (3.2) leads to the following inequalities:

Adding up, one obtains inequality (3.11) with , since A + B + C + 2D + 2E < 1. ■

Similar results concerning property (Q) of two self-mappings f and g (i.e., property that F(f) ∩ F(g) = F(fⁿ ) ∩ F(gⁿ ) for each n ∈ ℕ) can be obtained.