- Research Article
- Open access
- Published:
Solving the Set Equilibrium Problems
Fixed Point Theory and Applications volume 2011, Article number: 945413 (2011)
Abstract
We study the weak solutions and strong solutions of set equilibrium problems in real Hausdorff topological vector space settings. Several new results of existence for the weak solutions and strong solutions of set equilibrium problems are derived. The new results extend and modify various existence theorems for similar problems.
1. Introduction and Preliminaries
Let  ,
,  ,
,  be arbitrary real Hausdorff topological vector spaces, let
be arbitrary real Hausdorff topological vector spaces, let  be a nonempty closed convex set of
be a nonempty closed convex set of  , and let
, and let  be a proper closed convex and pointed cone with apex at the origin and
be a proper closed convex and pointed cone with apex at the origin and  , that is,
, that is,  is proper closed with
is proper closed with  and satisfies the following conditions:
and satisfies the following conditions:
(1) , for all
, for all  ;
;
(2) ;
;
(3) .
.
Letting  ,
,  be two sets of
be two sets of  , we can define relations "
, we can define relations " " and "
" and " " as follows:
" as follows:
(1)

 ;
;
(2)

 .
.
Similarly, we can define the relations " " and "
" and " " if we replace the set
" if we replace the set  by
by  .
.
The trimapping  and mapping
and mapping  are given. The set equilibrium problem (SEP)
I
is to find an
are given. The set equilibrium problem (SEP)
I
is to find an  such that
such that

for all  and for some
and for some  . Such solution is called a weak solution for (SEP)
I
. We note that (1.1) is equivalent to the following one:
. Such solution is called a weak solution for (SEP)
I
. We note that (1.1) is equivalent to the following one:

for all  and for some
and for some  .
.
For the case when  does not depend on
does not depend on  , that is, to find an
, that is, to find an  with some
with some  such that
such that

for all  , we will call this solution a strong solution of (SEP)
I
. We also note that (1.3) is equivalent to the following one:
, we will call this solution a strong solution of (SEP)
I
. We also note that (1.3) is equivalent to the following one:

for all  .
.
We note that if  is a vector-valued function and the mapping
is a vector-valued function and the mapping  is constant for each
is constant for each  , then (SEP)
I
reduces to the vector equilibrium problem (VEP), which is to find
, then (SEP)
I
reduces to the vector equilibrium problem (VEP), which is to find  such that
such that

for all  . Existence of a solution of this problem is investigated by Ansari et al. [1, 2].
. Existence of a solution of this problem is investigated by Ansari et al. [1, 2].
If  is a vector-valued function and
is a vector-valued function and  which is denoted the space of all continuous linear mappings from
which is denoted the space of all continuous linear mappings from  to
to  and
and  , where
, where  denotes the evaluation of the linear mapping
denotes the evaluation of the linear mapping  at
at  , then (SEP)
I
reduces to (GVVIP): to find
, then (SEP)
I
reduces to (GVVIP): to find  and
and  such that
such that

for all  . It has been studied by Chen and Craven [3].
. It has been studied by Chen and Craven [3].
If we consider  ,
,  ,
,  , and
, and 
 , where
, where  denotes the evaluation of the linear mapping
denotes the evaluation of the linear mapping  at
at  , then (SEP)
I
reduces to the (GVVIP) which is discussed by Huang and Fang [4] and Zeng and Yao [5]: to find a vector
, then (SEP)
I
reduces to the (GVVIP) which is discussed by Huang and Fang [4] and Zeng and Yao [5]: to find a vector  and
and  such that
such that

If  ,
,  is a single-valued mapping,
is a single-valued mapping,  , then (SEP)
I
reduces to the (weak) vector variational inequalities problem which is considered by Fang and Huang [6], Chiang and Yao [7], and Chiang [8] as follows: to find a vector
, then (SEP)
I
reduces to the (weak) vector variational inequalities problem which is considered by Fang and Huang [6], Chiang and Yao [7], and Chiang [8] as follows: to find a vector  such that
such that

for all  . The vector variational inequalities problem was first introduced by Giannessi [9] in finite-dimensional Euclidean space.
. The vector variational inequalities problem was first introduced by Giannessi [9] in finite-dimensional Euclidean space.
Summing up the above arguments, they show that for a suitable choice of the mapping  and the spaces
and the spaces  ,
,  , and
, and  , we can obtain a number of known classes of vector equilibrium problems, vector variational inequalities, and implicit generalized variational inequalities. It is also well known that variational inequality and its variants enable us to study many important problems arising in mathematical, mechanics, operations research, engineering sciences, and so forth.
, we can obtain a number of known classes of vector equilibrium problems, vector variational inequalities, and implicit generalized variational inequalities. It is also well known that variational inequality and its variants enable us to study many important problems arising in mathematical, mechanics, operations research, engineering sciences, and so forth.
In this paper we aim to derive some solvabilities for the set equilibrium problems. We also study some results of existence for the weak solutions and strong solutions of set equilibrium problems. Let  be a nonempty subset of a topological vector space
be a nonempty subset of a topological vector space  . A set-valued function
. A set-valued function  from
from  into the family of subsets of
into the family of subsets of  is a KKM mapping if for any nonempty finite set
is a KKM mapping if for any nonempty finite set  , the convex hull of
, the convex hull of  is contained in
is contained in  . Let us first recall the following results.
. Let us first recall the following results.
Fan's Lemma (see [10]).
Let  be a nonempty subset of Hausdorff topological vector space
be a nonempty subset of Hausdorff topological vector space  . Let
. Let  be a KKM mapping such that for any
be a KKM mapping such that for any  ,
,  is closed and
is closed and  is compact for some
is compact for some  . Then there exists
. Then there exists  such that
such that  for all
for all  .
.
Definition 1.1 (see [11]).
Let  be a vector space, let
be a vector space, let  be a topological vector space, let
be a topological vector space, let  be a nonempty convex subset of
be a nonempty convex subset of  , and let
, and let  be a proper closed convex and pointed cone with apex at the origin and
be a proper closed convex and pointed cone with apex at the origin and  , and
, and  is said to be
is said to be
(1) -convex if
-convex if  for every
for every  and
and  ;
;
(2)naturally quasi -convex if
-convex if  for every
for every  and
and  .
.
The following definition can also be found in [11].
Definition 1.2.
Let  be a Hausdorff topological vector space, let
be a Hausdorff topological vector space, let  be a proper closed convex and pointed cone with apex at the origin and
be a proper closed convex and pointed cone with apex at the origin and  , and let
, and let  be a nonempty subset of
be a nonempty subset of  . Then
. Then
(1)a point  is called a minimal point of
is called a minimal point of  if
if  ;
;  is the set of all minimal points of
is the set of all minimal points of  ;
;
(2)a point  is called a maximal point of
is called a maximal point of  if
if  ;
;  is the set of all maximal points of
is the set of all maximal points of  ;
;
(3)a point  is called a weakly minimal point of
is called a weakly minimal point of  if
if  ;
;  is the set of all weakly minimal points of
is the set of all weakly minimal points of  ;
;
(4)a point  is called a weakly maximal point of
is called a weakly maximal point of  if
if  ;
;  is the set of all weakly maximal points of
is the set of all weakly maximal points of  .
.
Definition 1.3.
Let  ,
,  be two topological spaces. A mapping
be two topological spaces. A mapping  is said to be
is said to be
(1)upper semicontinuous if for every  and every open set
and every open set  in
in  with
with  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that  ;
;
(2)lower semicontinuous if for every  and every open neighborhood
and every open neighborhood  of every
of every  , there exists a neighborhood
, there exists a neighborhood  of
of  such that
such that  for all
for all  ;
;
(3)continuous if it is both upper semicontinuous and lower semicontinuous.
We note that  is lower semicontinuous at
is lower semicontinuous at  if for any net
if for any net  ,
,  ,
,  implies that there exists net
implies that there exists net  such that
such that  . For other net-terminology properties about these two mappings, one can refer to [12].
. For other net-terminology properties about these two mappings, one can refer to [12].
Lemma 1.4 (see [13]).
Let  ,
,  , and
, and  be real topological vector spaces, and let
be real topological vector spaces, and let  and
and  be nonempty subsets of
be nonempty subsets of  and
and  , respectively. Let
, respectively. Let  ,
,  be set-valued mappings. If both
be set-valued mappings. If both  and
and  are upper semicontinuous with nonempty compact values, then the set-valued mapping
are upper semicontinuous with nonempty compact values, then the set-valued mapping  defined by
defined by

is upper semicontinuous with nonempty compact values.
By using similar technique of [11, Proposition 2.1], we can deduce the following lemma that slight-generalized the original one.
Lemma 1.5.
Let  ,
,  be two Hausdorff topological vector spaces, and let
be two Hausdorff topological vector spaces, and let  ,
,  be nonempty compact convex subsets of
be nonempty compact convex subsets of  and
and  , respectively. Let
, respectively. Let  be continuous mapping with nonempty compact valued on
be continuous mapping with nonempty compact valued on  ; the mapping
; the mapping  is naturally quasi
is naturally quasi  -convex on
-convex on  for each
for each  , and the mapping
, and the mapping  is
is  -convex on
-convex on  for each
for each  . Assume that for each
. Assume that for each  , there exists
, there exists  such that
such that

Then, one has

2. Existence Theorems for Set Equilibrium Problems
Now, we state and show our main results of solvabilities for set equilibrium problems.
Theorem 2.1.
Let  ,
,  ,
,  be real Hausdorff topological vector spaces, let
be real Hausdorff topological vector spaces, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be a proper closed convex and pointed cone with apex at the origin and
be a proper closed convex and pointed cone with apex at the origin and  . Given mappings
. Given mappings  ,
,  , and
, and  , suppose that
, suppose that
(1) for all
for all  ;
;
(2)for each  , there is an
, there is an  such that for all
such that for all  ,
,

(3)for each  , the set
, the set  is convex;
is convex;
(4)there is a nonempty compact convex subset  of
of  , such that for every
, such that for every  , there is a
, there is a  such that for all
such that for all  ,
,

-
(5)
for each
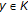 , the set
, the set 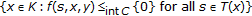 is open in
is open in  .
.
Then there exists an  which is a weak solution of (SEP)I. That is, there is an
which is a weak solution of (SEP)I. That is, there is an  such that
such that

for all  and for some
and for some  .
.
Proof.
Define  by
by

for all  . From condition (5) we know that for each
. From condition (5) we know that for each  , the set
, the set  is closed in
is closed in  , and hence it is compact in
, and hence it is compact in  because of the compactness of
because of the compactness of  .
.
Next, we claim that the family  has the finite intersection property, and then the whole intersection
has the finite intersection property, and then the whole intersection  is nonempty and any element in the intersection
is nonempty and any element in the intersection  is a solution of (SEP)
I
, for any given nonempty finite subset
is a solution of (SEP)
I
, for any given nonempty finite subset  of
of  . Let
. Let  , the convex hull of
, the convex hull of  . Then
. Then  is a compact convex subset of
is a compact convex subset of  . Define the mappings
. Define the mappings  , respectively, by
, respectively, by

for each  . From conditions (1) and (2), we have
. From conditions (1) and (2), we have

and for each  , there is an
, there is an  such that
such that

Hence  , and then
, and then  for all
for all  .
.
We can easily see that  has closed values in
has closed values in  . Since, for each
. Since, for each  ,
,  , if we prove that the whole intersection of the family
, if we prove that the whole intersection of the family  is nonempty, we can deduce that the family
is nonempty, we can deduce that the family  has finite intersection property because
has finite intersection property because  and due to condition (4). In order to deduce the conclusion of our theorem, we can apply Fan's lemma if we claim that
and due to condition (4). In order to deduce the conclusion of our theorem, we can apply Fan's lemma if we claim that  is a KKM mapping. Indeed, if
is a KKM mapping. Indeed, if  is not a KKM mapping, neither is
is not a KKM mapping, neither is  since
since  for each
for each  . Then there is a nonempty finite subset
. Then there is a nonempty finite subset  of
of  such that
such that

Thus there is an element  such that
such that  for all
for all  , that is,
, that is,  for all
for all  . By (3), we have
. By (3), we have

and hence  which contradicts (2.6). Hence
which contradicts (2.6). Hence  is a KKM mapping, and so is
is a KKM mapping, and so is  . Therefore, there exists an
. Therefore, there exists an  which is a solution of (SEP)
I
. This completes the proof.
which is a solution of (SEP)
I
. This completes the proof.
Theorem 2.2.
Let  ,
,  ,
,  be real Hausdorff topological vector spaces, let
be real Hausdorff topological vector spaces, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be a proper closed convex and pointed cone with apex at the origin and
be a proper closed convex and pointed cone with apex at the origin and  . Let the mapping
. Let the mapping  be such that for each
be such that for each  , the mappings
, the mappings  and
and  are upper semicontinuous with nonempty compact values and
are upper semicontinuous with nonempty compact values and  . Suppose that conditions (1)–(4) of Theorem 2.1 hold. Then there exists an
. Suppose that conditions (1)–(4) of Theorem 2.1 hold. Then there exists an  which is a solution of (SEP)I. That is, there is an
which is a solution of (SEP)I. That is, there is an  such that
such that

for all  and for some
and for some  .
.
Proof.
For any fixed  , we define the mapping
, we define the mapping  by
by

for all  and
and  . Since the mappings
. Since the mappings  and
and  are upper semicontinuous with nonempty compact values, by Lemma 1.4, we know that
are upper semicontinuous with nonempty compact values, by Lemma 1.4, we know that  is upper semicontinuous on
is upper semicontinuous on  with nonempty compact values. Hence, for each
with nonempty compact values. Hence, for each  , the set
, the set

is open in  . Then all conditions of Theorem 2.1 hold. From Theorem 2.1, (SEP)
I
has a solution.
. Then all conditions of Theorem 2.1 hold. From Theorem 2.1, (SEP)
I
has a solution.
In order to discuss the results of existence for the strong solution of (SEP)
I
, we introduce the condition (). It is obviously fulfilled that if  ,
,  is single-valued function.
is single-valued function.
Theorem 2.3.
Under the framework of Theorem 2.2, one has a weak solution  of (SEP)I with
of (SEP)I with  . In addition, if
. In addition, if  ,
,  , and
, and  is compact,
is compact,  is convex, the mapping
is convex, the mapping  is continuous with nonempty compact valued on
is continuous with nonempty compact valued on  , the mapping
, the mapping  is naturally quasi
is naturally quasi  -convex on
-convex on  for each
for each  , and the mapping
, and the mapping  is
is  -convex on
-convex on  for each
for each  . Assuming that for each
. Assuming that for each  , there exists
, there exists  such that
such that

then  is a strong solution of (SEP)I; that is, there exists
is a strong solution of (SEP)I; that is, there exists  such that
such that

for all  . Furthermore, the set of all strong solutions of (SEP)I is compact.
. Furthermore, the set of all strong solutions of (SEP)I is compact.
Proof.
From Theorem 2.2, we know that  such that (1.1) holds for all
such that (1.1) holds for all  and for some
and for some  . Then we have
. Then we have  .
.
From condition () and the convexity of  , Lemma 1.5 tells us that
, Lemma 1.5 tells us that  . Then there is an
. Then there is an  such that
such that  . Thus for all
. Thus for all  , we have
, we have  . Hence there exists
. Hence there exists  such that
such that

for all  . Such an
. Such an  is a strong solution of (SEP)
I
.
is a strong solution of (SEP)
I
.
Finally, to see that the solution set of (SEP)
I
is compact, it is sufficient to show that the solution set is closed due to the coercivity condition (4) of Theorem 2.2. To this end, let  denote the solution set of (SEP)
I
. Suppose that net
denote the solution set of (SEP)
I
. Suppose that net  which converges to some
which converges to some  . Fix any
. Fix any  . For each
. For each  , there is an
, there is an  such that
such that

Since  is upper semicontinuous with compact values and the set
is upper semicontinuous with compact values and the set  is compact, it follows that
is compact, it follows that  is compact. Therefore without loss of generality, we may assume that the sequence
is compact. Therefore without loss of generality, we may assume that the sequence  converges to some
converges to some  . Then
. Then  and
and  . Let
. Let 
 . Since the mapping
. Since the mapping  is upper semicontinuous with nonempty compact values, the set
is upper semicontinuous with nonempty compact values, the set  is open in
is open in  . Hence
. Hence  is closed in
is closed in  . By the facts
. By the facts  and
and  , we have
, we have  . This implies that
. This implies that  . We then obtain
. We then obtain

Hence  and
and  is closed.
is closed.
We would like to point out that condition () is fulfilled if we take  and
and  is a single-valued function. The following is a concrete example for both Theorems 2.1 and 2.3.
is a single-valued function. The following is a concrete example for both Theorems 2.1 and 2.3.
Example 2.4.
Let  ,
,  ,
,  ,
,  , and
, and  . Choose
. Choose  to be defined by
to be defined by  for every
for every  and
and  is defined by
is defined by  , where
, where  ,
,  with
with  , for some
, for some  ,
,  , and
, and  is defined by
is defined by

Then all conditions of Theorems 2.1 and 2.3 are satisfied. By Theorems 2.1 and 2.3, respectively, the (SEP)
I
not only has a weak solution, but also has a strong solution. A simple geometric discussion tells us that  is a strong solution for (SEP)
I
.
is a strong solution for (SEP)
I
.
Corollary 2.5.
Under the framework of Theorem 2.1, one has a weak solution  of (SEP)I with
of (SEP)I with  . In addition, if
. In addition, if  and
and  ,
,  is compact,
is compact,  is convex,
is convex,  -convex on
-convex on  for each
for each  and the mapping
and the mapping  is
is  -convex on
-convex on  for each
for each  ,
,  such that
such that  is continuous with nonempty compact values for each
is continuous with nonempty compact values for each  , and
, and  is upper semicontinuous with nonempty compact values. Assume that condition () holds, then
is upper semicontinuous with nonempty compact values. Assume that condition () holds, then  is a strong solution of (SEP)I; that is, there exists
is a strong solution of (SEP)I; that is, there exists  such that
such that

for all  . Furthermore, the set of all strong solutions of (SEP)I is compact.
. Furthermore, the set of all strong solutions of (SEP)I is compact.
Theorem 2.6.
Let  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  be as in Theorem 2.1. Assume that the mapping
be as in Theorem 2.1. Assume that the mapping  is
is  -convex on
-convex on  for each
for each  and
and  such that
such that
(1)for each  , there is an
, there is an  such that
such that  ;
;
(2)there is a nonempty compact convex subset  of
of  , such that for every
, such that for every  , there is a
, there is a  such that for all
such that for all  ,
,

(3)for each  , the set
, the set  is open in
is open in  .
.
Then there is an  which is a weak solution of (SEP)I.
which is a weak solution of (SEP)I.
Proof.
For any given nonempty finite subset  of
of  . Letting
. Letting  , then
, then  is a nonempty compact convex subset of
is a nonempty compact convex subset of  . Define
. Define  as in the proof of Theorem 2.1, and for each
as in the proof of Theorem 2.1, and for each  , let
, let

We note that for each  ,
,  is nonempty and closed since
is nonempty and closed since  by conditions (1) and (3). For each
by conditions (1) and (3). For each  ,
,  is compact in
is compact in  . Next, we claim that the mapping
. Next, we claim that the mapping  is a KKM mapping. Indeed, if not, there is a nonempty finite subset
is a KKM mapping. Indeed, if not, there is a nonempty finite subset  of
of  , such that
, such that  . Then there is an
. Then there is an  such that
such that

for all  and
and  . Since the mapping
. Since the mapping

is  -convex on
-convex on  , we can deduce that
, we can deduce that

for all  . This contradicts condition (1). Therefore,
. This contradicts condition (1). Therefore,  is a KKM mapping, and by Fan's lemma, we have
is a KKM mapping, and by Fan's lemma, we have  . Note that for any
. Note that for any  , we have
, we have  by condition (2). Hence, we have
by condition (2). Hence, we have

for each nonempty finite subset  of
of  . Therefore, the whole intersection
. Therefore, the whole intersection  is nonempty. Let
is nonempty. Let  . Then
. Then  is a solution of (SEP)
I
.
is a solution of (SEP)
I
.
Corollary 2.7.
Let  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  be as in Theorem 2.1. Assume that the mapping
be as in Theorem 2.1. Assume that the mapping  is
is  -convex on
-convex on  for each
for each  and
and  ,
,  such that
such that  is continuous with nonempty compact values for each
is continuous with nonempty compact values for each  , and
, and  is upper semicontinuous with nonempty compact values. Suppose that
is upper semicontinuous with nonempty compact values. Suppose that
(1)for each  , there is an
, there is an  such that
such that  ;
;
(2)there is a nonempty compact convex subset  of
of  , such that for every
, such that for every  , there is a
, there is a  such that for all
such that for all  ,
,

Then there is an  which is a weak solution of (SEP)I.
which is a weak solution of (SEP)I.
Proof.
Using the technique of the proof in Theorem 2.2 and applying Theorem 2.6, we have the conclusion.
The following result is another existence theorem for the strong solutions of (SEP) . We need to combine Theorem 2.6 and use the technique of the proof in Theorem 2.3.
. We need to combine Theorem 2.6 and use the technique of the proof in Theorem 2.3.
Theorem 2.8.
Under the framework of Theorem 2.6, on has a weak solution  of (SEP)I with
of (SEP)I with  . In addition, if
. In addition, if  and
and  ,
,  is compact,
is compact,  is convex and the mapping
is convex and the mapping  is naturally quasi
is naturally quasi  -convex on
-convex on  for each
for each  ,
,  such that
such that  is continuous with nonempty compact values for each
is continuous with nonempty compact values for each  , and
, and  is upper semicontinuous with nonempty compact values. Assuming that condition () holds, then
is upper semicontinuous with nonempty compact values. Assuming that condition () holds, then  is a strong solution of (SEP)I; that is, there exists
is a strong solution of (SEP)I; that is, there exists  such that
such that

for all  . Furthermore, the set of all strong solutions of (SEP)I is compact.
. Furthermore, the set of all strong solutions of (SEP)I is compact.
Using the technique of the proof in Theorem 2.3, we have the following result.
Corollary 2.9.
Under the framework of Corollary 2.7, one has a weak solution  of (SEP)I with
of (SEP)I with  . In addition, if
. In addition, if  and
and  ,
,  is compact,
is compact,  is convex, and the mapping
is convex, and the mapping  is naturally quasi
is naturally quasi  -convex on
-convex on  for each
for each  . Assuming that condition () holds, then
. Assuming that condition () holds, then  is a strong solution of (SEP)I; that is, there exists
is a strong solution of (SEP)I; that is, there exists  such that
such that

for all  . Furthermore, the set of all strong solutions of (SEP)I is compact.
. Furthermore, the set of all strong solutions of (SEP)I is compact.
Next, we discuss the existence results of the strong solutions for (SEP)
I
with the set  without compactness setting from Theorems 2.10 to 2.14 below.
without compactness setting from Theorems 2.10 to 2.14 below.
Theorem 2.10.
Letting  be a finite-dimensional real Banach space, under the framework of Theorem 2.1, one has a weak solution
be a finite-dimensional real Banach space, under the framework of Theorem 2.1, one has a weak solution  of (SEP)I with
of (SEP)I with  . In addition, if
. In addition, if  and
and  ,
,  is convex,
is convex,  for all
for all  and for all
and for all  , the mapping
, the mapping  is
is  -convex on
-convex on  for each
for each  and
and  and the mapping
and the mapping  is naturally quasi
is naturally quasi  -convex on
-convex on  for each
for each  ,
,  such that
such that  is continuous for each
is continuous for each  , and
, and  is upper semicontinuous with nonempty compact values. Assume that for some
is upper semicontinuous with nonempty compact values. Assume that for some  , such that for each
, such that for each  , there is a
, there is a  such that the condition
such that the condition

is satisfied, where  . Then
. Then  is a strong solution of (SEP)I; that is, there exists
is a strong solution of (SEP)I; that is, there exists  such that
such that

for all  . Furthermore, the set of all strong solutions of (SEP)I is compact.
. Furthermore, the set of all strong solutions of (SEP)I is compact.
Proof.
Let us choose  such that condition () holds. Letting
such that condition () holds. Letting  , then the set
, then the set  is nonempty and compact in
is nonempty and compact in  . We replace
. We replace  by
by  in Theorem 2.3; all conditions of Theorem 2.3 hold. Hence by Theorem 2.3, we have
in Theorem 2.3; all conditions of Theorem 2.3 hold. Hence by Theorem 2.3, we have  such that
such that

for all  . For any
. For any  , choose
, choose  small enough such that
small enough such that  . Putting
. Putting  in (2.29), we have
in (2.29), we have

We note that

which implies that

for all  . This completely proves the theorem.
. This completely proves the theorem.
Corollary 2.11.
Letting  be a finite-dimensional real Banach space, under the framework of Theorem 2.2, one has a weak solution
be a finite-dimensional real Banach space, under the framework of Theorem 2.2, one has a weak solution  of (SEP)I with
of (SEP)I with  . In addition, if
. In addition, if  and
and  ,
,  is convex,
is convex,  for all
for all  and for all
and for all  , the mapping
, the mapping  is
is  -convex on
-convex on  for each
for each  and
and  , and the mapping
, and the mapping  is naturally quasi
is naturally quasi  -convex on
-convex on  for each
for each  . Assume that for some
. Assume that for some  , condition () holds. Then
, condition () holds. Then  is a strong solution of (SEP)I; that is, there exists
is a strong solution of (SEP)I; that is, there exists  such that
such that

for all  Furthermore, the set of all strong solutions of (SEP)I is compact.
Furthermore, the set of all strong solutions of (SEP)I is compact.
Using a similar argument to that of the proof in Theorem 2.10 and combining Theorem 2.6 and Corollary 2.7, respectively, we have the following two results of existence for the strong solution of (SEP) I .
Theorem 2.12.
Let  be a finite-dimensional real Banach space, under the framework of Theorem 2.6, one has a weak solution
be a finite-dimensional real Banach space, under the framework of Theorem 2.6, one has a weak solution  of (SEP)I with
of (SEP)I with  . In addition, if
. In addition, if  and
and  ,
,  is convex,
is convex,  for all
for all  and for all
and for all  , the mapping
, the mapping  is naturally quasi
is naturally quasi  -convex on
-convex on  for each
for each  ,
,  such that
such that  is continuous for each
is continuous for each  , and
, and  is upper semicontinuous with nonempty compact values. Assume that for some
is upper semicontinuous with nonempty compact values. Assume that for some  , condition () holds. Then
, condition () holds. Then  is a strong solution of (SEP)I; that is, there exists
is a strong solution of (SEP)I; that is, there exists  such that
such that

for all  . Furthermore, the set of all strong solutions of (SEP)I is compact.
. Furthermore, the set of all strong solutions of (SEP)I is compact.
In order to illustrate Theorems 2.10 and 2.12 more precisely, we provide the following concrete example.
Example 2.13.
Let  ,
,  ,
,  ,
,  , and
, and  . Choose
. Choose  to be defined by
to be defined by  for every
for every  and
and  is defined by
is defined by  , where
, where  ,
,  , and
, and  is defined by
is defined by

We claim that condition () holds. Indeed, We know that the weak solution  . For each
. For each  , if we choose any
, if we choose any  , then
, then  and
and 
 . Hence condition () and all other conditions of Theorems 2.10 and 2.12 are satisfied. By Theorems 2.10 and 2.12, respectively, the (SEP)
I
not only has a weak solution, but also has a strong solution. We can see that
. Hence condition () and all other conditions of Theorems 2.10 and 2.12 are satisfied. By Theorems 2.10 and 2.12, respectively, the (SEP)
I
not only has a weak solution, but also has a strong solution. We can see that  is a strong solution for (SEP)
I
.
is a strong solution for (SEP)
I
.
Theorem 2.14.
Letting  be a finite-dimensional real Banach space, under the framework of Corollary 2.7, one has a weak solution
be a finite-dimensional real Banach space, under the framework of Corollary 2.7, one has a weak solution  of (SEP)I with
of (SEP)I with  . In addition, if
. In addition, if  and
and  ,
,  is convex,
is convex,  for all
for all  and for all
and for all  , and the mapping
, and the mapping  is naturally quasi
is naturally quasi  -convex on
-convex on  for each
for each  . Assume that for some
. Assume that for some  , condition () holds. Then
, condition () holds. Then  is a strong solution of (SEP)I; that is, there exists
is a strong solution of (SEP)I; that is, there exists  such that
such that

for all  . Furthermore, the set of all strong solutions of (SEP)I is compact.
. Furthermore, the set of all strong solutions of (SEP)I is compact.
We would like to point out an open question naturally arising from Theorem 2.3: is Theorem 2.3 extendable to the case of  or more general spaces, such as Hausdorff topological vector spaces?
or more general spaces, such as Hausdorff topological vector spaces?
References
Ansari QH, Konnov IV, Yao JC: Existence of a solution and variational principles for vector equilibrium problems. Journal of Optimization Theory and Applications 2001,110(3):481–492. 10.1023/A:1017581009670
Ansari QH, Oettli W, Schläger D: A generalization of vectorial equilibria. Mathematical Methods of Operations Research 1997,46(2):147–152. 10.1007/BF01217687
Chen G-Y, Craven BD: A vector variational inequality and optimization over an efficient set. Zeitschrift für Operations Research 1990,34(1):1–12.
Huang N-J, Fang Y-P: On vector variational inequalities in reflexive Banach spaces. Journal of Global Optimization 2005,32(4):495–505. 10.1007/s10898-003-2686-z
Zeng L-C, Yao Jen-Chih: Existence of solutions of generalized vector variational inequalities in reflexive Banach spaces. Journal of Global Optimization 2006,36(4):483–497. 10.1007/s10898-005-5509-6
Fang Y-P, Huang N-J: Strong vector variational inequalities in Banach spaces. Applied Mathematics Letters 2006,19(4):362–368. 10.1016/j.aml.2005.06.008
Chiang Y, Yao JC: Vector variational inequalities and the
 condition. Journal of Optimization Theory and Applications 2004, 123(2):271–290. 10.1007/s10957-004-5149-x
condition. Journal of Optimization Theory and Applications 2004, 123(2):271–290. 10.1007/s10957-004-5149-xChiang Y: The
 -condition for vector equilibrium problems. Taiwanese Journal of Mathematics 2006,10(1):31–43.
-condition for vector equilibrium problems. Taiwanese Journal of Mathematics 2006,10(1):31–43.Giannessi F: Theorems of alternative, quadratic programs and complementarity problems. In Variational Inequalities and Complementarity Problems. Edited by: Cottle RW, Giannessi F, Lions LJL. Wiley, Chichester, UK; 1980:151–186.
Fan K: A generalization of Tychonoff's fixed point theorem. Mathematische Annalen 1961, 142: 305–310. 10.1007/BF01353421
Li SJ, Chen GY, Lee GM: Minimax theorems for set-valued mappings. Journal of Optimization Theory and Applications 2000,106(1):183–199. 10.1023/A:1004667309814
Aubin J-P, Cellina A: Differential Inclusions: Set-Valued Maps and Viability Theory, Grundlehren der Mathematischen Wissenschaften. Volume 264. Springer, Berlin, Germany; 1984:xiii+342.
Lin L-J, Yu Z-T: On some equilibrium problems for multimaps. Journal of Computational and Applied Mathematics 2001,129(1–2):171–183. 10.1016/S0377-0427(00)00548-3
Acknowledgments
The authors would like to thank the referees whose remarks helped improving the paper. This work was partially supported by Grant no. 98-Edu-Project7-B-55 of Ministry of Education of Taiwan (Republic of China) and Grant no. NSC98-2115-M-039-001- of the National Science Council of Taiwan (Republic of China) that are gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lin, YC., Chen, HJ. Solving the Set Equilibrium Problems. Fixed Point Theory Appl 2011, 945413 (2011). https://doi.org/10.1155/2011/945413
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/945413
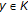 , the set
, the set 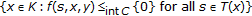 is open in
is open in  .
. condition. Journal of Optimization Theory and Applications 2004, 123(2):271–290. 10.1007/s10957-004-5149-x
condition. Journal of Optimization Theory and Applications 2004, 123(2):271–290. 10.1007/s10957-004-5149-x -condition for vector equilibrium problems. Taiwanese Journal of Mathematics 2006,10(1):31–43.
-condition for vector equilibrium problems. Taiwanese Journal of Mathematics 2006,10(1):31–43.