- Research Article
- Open access
- Published:
Iterative Algorithms for Finding Common Solutions to Variational Inclusion Equilibrium and Fixed Point Problems
Fixed Point Theory and Applications volume 2011, Article number: 915629 (2011)
Abstract
The main purpose of this paper is to introduce an explicit iterative algorithm to study the existence problem and the approximation problem of solution to the quadratic minimization problem. Under suitable conditions, some strong convergence theorems for a family of nonexpansive mappings are proved. The results presented in the paper improve and extend the corresponding results announced by some authors.
1. Introduction
Throughout this paper, we assume that  is a real Hilbert space with inner product
is a real Hilbert space with inner product  and norm
and norm  ,
,  is a nonempty closed convex subset of
is a nonempty closed convex subset of  , and
, and  is the set of fixed points of mapping
is the set of fixed points of mapping  .
.
A mapping  is called nonexpansive if
is called nonexpansive if

Let  be a single-valued nonlenear mapping and
be a single-valued nonlenear mapping and  be a multivalued mapping. The so-called quasivariational inclusion problem (see [1–3]) is to find
be a multivalued mapping. The so-called quasivariational inclusion problem (see [1–3]) is to find  such that
such that

The set of solutions to quasivariational inclusion problem (1.2) is denoted by  .
.
Special Cases
-
(I)
If
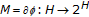 , where
, where  is a proper convex lower semi-continuous function and
is a proper convex lower semi-continuous function and 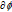 is the subdifferential of
is the subdifferential of  , then the quasivariational inclusion problem (1.2) is equivalent to finding
, then the quasivariational inclusion problem (1.2) is equivalent to finding 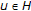 such that
such that 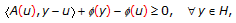 (1.3)
(1.3)
which is called the mixed quasivariational inequality (see [4]).
-
(II)
If
 , where
, where  is a nonempty closed convex subset of
is a nonempty closed convex subset of 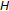 and
and 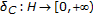 is the indicator function of
is the indicator function of  , that is,
, that is, 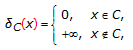 (1.4)
(1.4)
then the quasivariational inclusion problem (1.2) is equivalent to finding  such that
such that

This problem is called the Hartman-Stampacchia variational inequality (see [5]). The set of solutions to variational inequality (1.5) is denoted by  .
.
Let  be a nonlinear mapping and
be a nonlinear mapping and  be a bifunction. The so-called generalized equilibrium problem is to find a point
be a bifunction. The so-called generalized equilibrium problem is to find a point  such that
such that

The set of solutions to (1.6) is denoted by GEP (see [5, 6]). If  , then (1.6) reduces to the following equilibrium problem: to find
, then (1.6) reduces to the following equilibrium problem: to find  such that
such that

The set of solutions to (1.7) is denoted by EP.
Iterative methods for nonexpansive mappings and equilibrium problems have been applied to solve convex minimization problems (see [7–9]). A typical problem is to minimize a quadratic function over the set of the fixed points of a nonexpansive mapping on a real Hilbert space  :
:

where  is the fixed point set of a nonexpansive mapping
is the fixed point set of a nonexpansive mapping  on
on  .
.
In 2010, Zhang et al. (see [10]) proposed the following iteration method for variational inclusion problem (1.5) and equilibrium problem (1.6) in a Hilbert space  :
:

Under suitable conditions, they proved the sequence  generated by (1.9) converges strongly to the fixed point
generated by (1.9) converges strongly to the fixed point  , which solves the quadratic minimization problem (1.8).
, which solves the quadratic minimization problem (1.8).
Motivated and inspired by the researches going on in this direction, especially inspired by Zhang et al. [10], the purpose of this paper is to introduce an explicit iterative algorithm to studying the existence problem and the approximation problem of the solution to the quadratic minimization problem (1.8) and prove some strong convergence theorems for a family of nonexpansive mappings in the setting of Hilbert spaces.
2. Preliminaries
Let  be a real Hilbert space, and
be a real Hilbert space, and  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . For any
. For any  , there exists a unique nearest point in
, there exists a unique nearest point in  , denoted by
, denoted by  , such that
, such that

Such a mapping  from
from  onto
onto  is called the metric projection. It is well-known that the metric projection
is called the metric projection. It is well-known that the metric projection  is nonexpansive.
is nonexpansive.
In the sequel, we use  and
and  to denote the weak convergence and the strong convergence of the sequence
to denote the weak convergence and the strong convergence of the sequence  , respectively.
, respectively.
Definition 2.1.
A mapping  is called
is called  -inverse strongly monotone if there exists an
-inverse strongly monotone if there exists an  such that
such that

A multivalued mapping  is called monotone if
is called monotone if  ,
,

A multivalued mapping  is called maximal monotone if it is monotone and for any
is called maximal monotone if it is monotone and for any  , when
, when

then  .
.
Proposition 2.2 (see [11]).
Let  be an
be an  -inverse strongly monotone mapping. Then, the following statements hold:
-inverse strongly monotone mapping. Then, the following statements hold:
(i) is an
is an  -Lipschitz continuous and monotone mapping;
-Lipschitz continuous and monotone mapping;
(ii)if  is any constant in
is any constant in  , then the mapping
, then the mapping  is nonexpansive, where
is nonexpansive, where  is the identity mapping on
is the identity mapping on  .
.
Lemma 2.3 (see [12]).
Let  be a strictly convex Banach space,
be a strictly convex Banach space,  be a closed convex subset of
be a closed convex subset of  , and
, and  be a sequence of nonexpansive mappings. Suppose
be a sequence of nonexpansive mappings. Suppose  . Let
. Let  be a sequence of positive numbers with
be a sequence of positive numbers with  . Then the mapping
. Then the mapping  defined by
defined by

is well defined. And it is nonexpansive and

Definition 2.4.
Let  be a Hilbert space and
be a Hilbert space and  be a multivalued maximal monotone mapping. Then, the single-valued mapping
be a multivalued maximal monotone mapping. Then, the single-valued mapping  defined by
defined by

is called the resolvent operator associated with , where
, where  is any positive number and
is any positive number and  is the identity mapping.
is the identity mapping.
Proposition 2.5 (see [11]).
-
(i)
The resolvent operator
 associated with
associated with 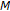 is single-valued and nonexpansive for all
is single-valued and nonexpansive for all  , that is,
, that is, 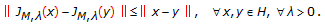 (2.8)
(2.8)
(ii) The resolvent operator  is 1-inverse strongly monotone, that is,
is 1-inverse strongly monotone, that is,

Definition 2.6.
A single-valued mapping  is said to be hemicontinuous if for any
is said to be hemicontinuous if for any  , function
, function  is continuous at 0.
is continuous at 0.
It is well-known that every continuous mapping must be hemicontinuous.
Lemma 2.7 (see [13]).
Let  and
and  be bounded sequences in a Banach space
be bounded sequences in a Banach space  . Let
. Let  be a sequence in
be a sequence in  with
with

Suppose that

Then,

Lemma 2.8 (see [14]).
Let  be a real Banach space,
be a real Banach space,  be the dual space of
be the dual space of  ,
,  be a maximal monotone mapping, and
be a maximal monotone mapping, and  be a hemicontinuous bound monotone mapping with
be a hemicontinuous bound monotone mapping with  . Then, the mapping
. Then, the mapping  is a maximal monotone mapping.
is a maximal monotone mapping.
Lemma 2.9 (see [15]).
Let  be a uniformly convex Banach space, let
be a uniformly convex Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and
, and  be a nonexpansive mapping with a fixed point. Then,
be a nonexpansive mapping with a fixed point. Then,  is demiclosed in the sense that if
is demiclosed in the sense that if  is a sequence in
is a sequence in  satisfying
satisfying

then

Throughout this paper, we assume that the bifunction  satisfies the following conditions:
satisfies the following conditions:
 for all
for all  ;
;
 is monotone, that is,
is monotone, that is,

for each  ,
,

for each  ,
,  is convex and lower semi-continuous.
is convex and lower semi-continuous.
Lemma 2.10 (see [16]).
Let  be a real Hilbert space,
be a real Hilbert space,  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and
, and  be a bifunction satisfying the conditions
be a bifunction satisfying the conditions  . Let
. Let  and
and  . Then, there exists a point
. Then, there exists a point  such that
such that

Moreover, if  is a mapping defined by
is a mapping defined by

then the following results hold:
(i) is single-valued and firmly nonexpansive, that is, for any
is single-valued and firmly nonexpansive, that is, for any  ,
,

(ii)EP is closed and convex, and  .
.
Lemma 2.11.
-
(i)
(see [11])
 is a solution of variational inclusion (1.2) if and only if
is a solution of variational inclusion (1.2) if and only if  (2.20)
(2.20)
that is,

-
(ii)
(see [10])
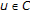 is a solution of generalized equilibrium problem (1.6) if and only if
is a solution of generalized equilibrium problem (1.6) if and only if 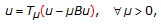 (2.22)
(2.22)
that is,

(iii) (see [10]) Let  be an
be an  -inverse strongly monotone mapping and
-inverse strongly monotone mapping and  be a
be a  -inverse strongly monotone mapping. If
-inverse strongly monotone mapping. If  and
and  , then
, then  is a closed convex subset in
is a closed convex subset in  and GEP is a closed convex subset in
and GEP is a closed convex subset in  .
.
Lemma 2.12 (see [17]).
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

where  is a sequence in
is a sequence in  and
and  is a sequence such that:
is a sequence such that:
(i) ;
;
(ii) or
or  .
.
Then,  .
.
3. Main Results
Theorem 3.1.
Let  be a real Hilbert space,
be a real Hilbert space,  be a nonempty closed convex subset of
be a nonempty closed convex subset of  ,
,  be an
be an  -inverse strongly monotone mapping and
-inverse strongly monotone mapping and  be a
be a  -inverse strongly monotone mapping. Let
-inverse strongly monotone mapping. Let  be a maximal monotone mapping,
be a maximal monotone mapping,  be a sequence of nonexpansive mappings with
be a sequence of nonexpansive mappings with  ,
,  be the nonexpansive mapping defined by (2.5), and
be the nonexpansive mapping defined by (2.5), and  be a bifunction satisfying conditions
be a bifunction satisfying conditions  . Let
. Let  be the sequence defined by
be the sequence defined by

where the mapping  is defined by (2.18), and
is defined by (2.18), and  are two constants with
are two constants with  , and
, and

If

where  and GEP is the set of solutions of variational inclusion (1.2) and generalized equilibrium problem (1.6), respectively, then the sequence
and GEP is the set of solutions of variational inclusion (1.2) and generalized equilibrium problem (1.6), respectively, then the sequence  defined by (3.1) converges strongly to
defined by (3.1) converges strongly to  , which is the unique solution of the following quadratic minimization problem:
, which is the unique solution of the following quadratic minimization problem:

Proof.
We divide the proof of Theorem 3.1 into four steps.
Step 1 (The sequence  is bounded).
is bounded).
Set

Taking  , then it follows from Lemma 2.11 that
, then it follows from Lemma 2.11 that

Since both  and
and  are nonexpansive,
are nonexpansive,  and
and  are
are  -inverse strongly monotone and
-inverse strongly monotone and  -inverse strongly monotone, respectively, from Proposition 2.2, we have
-inverse strongly monotone, respectively, from Proposition 2.2, we have


This implies that

It follows from (3.1) and (3.9) that

where  . This shows that
. This shows that  is bounded. Hence, it follows from (3.9) that the sequence
is bounded. Hence, it follows from (3.9) that the sequence  and
and  are also bounded.
are also bounded.
It follows from (3.5), (3.6), and (3.9) that

This shows that  is bounded.
is bounded.
Step 2.
Now, we prove that

Since  is nonexpansive, from (3.5) and (3.9), we have that
is nonexpansive, from (3.5) and (3.9), we have that


Let  in (3.14), in view of condition
in (3.14), in view of condition  , we have
, we have

By virtue of Lemma 2.7, we have

This implies that

We derive from (3.17) that

From (3.1) and (3.8), we have

where

that is,

Let  , noting the assumptions that
, noting the assumptions that  ,
,  , from (3.2) and (3.18), we have
, from (3.2) and (3.18), we have

By virtue of Lemma 2.10(i) and (3.1), we have

Simplifying it, we have

Similarly, in view of Proposition 2.5(ii) and (3.1), we have

Simplifying it, from (3.24), we have

From (3.19) and (3.26), we have

Let  nd in view of (3.18) and (3.22), we have
nd in view of (3.18) and (3.22), we have

This shows that

Then, we have

Step 3 (sequence  converges strongly to
converges strongly to  ).
).
Because  is bounded, without loss of generality, we can assume that
is bounded, without loss of generality, we can assume that  . In view of (3.12), it yields that
. In view of (3.12), it yields that  and
and  . From Lemma 2.9 and (3.30), we know that
. From Lemma 2.9 and (3.30), we know that  .
.
Next, we prove that  .
.
Since  , we have
, we have

It follows from condition  that
that

Therefore,

For any  and
and  , then
, then  . From (3.33), we have
. From (3.33), we have

Since  is
is  -inverse strongly monotone, from Proposition 2.2(i) and (3.12), we have
-inverse strongly monotone, from Proposition 2.2(i) and (3.12), we have

Let  in (3.34), in view of condition
in (3.34), in view of condition  and
and  , we have
, we have

It follows from conditions  ,
,  and (3.36) that
and (3.36) that

that is,

Let  to 0 in (3.38), we have
to 0 in (3.38), we have

This shows that  .
.
Step 4 (now, we prove that  ).
).
Since  is
is  -inverse strongly monotone, from Proposition 2.2 (i), we know that
-inverse strongly monotone, from Proposition 2.2 (i), we know that  is an
is an  -Lipschitz continuous and monotone mapping and
-Lipschitz continuous and monotone mapping and  , where
, where  is the domain of
is the domain of  . It follows from Lemma 2.8 that
. It follows from Lemma 2.8 that  is maximal monotone. Let
is maximal monotone. Let  , that is,
, that is,  . Since
. Since  , we have
, we have  , that is,
, that is,  . By virtue of the maximal monotonicity of
. By virtue of the maximal monotonicity of  , we have
, we have

Therefore we have

Since  is monotone, this implies that
is monotone, this implies that

Since

from (3.42), we have

Since  is maximal monotone,
is maximal monotone,  , that is,
, that is,  .
.
Summing up the above arguments, we have proved that

On the other hand, for any  , we have
, we have

and so we have

Put  in (3.47), we have
in (3.47), we have

where  and
and  . Since
. Since  , it is easy to see that
, it is easy to see that  and
and  . By Lemma 2.12, we conclude that
. By Lemma 2.12, we conclude that  as
as  , where
, where  is the unique solution of the following quadratic minimization problem:
is the unique solution of the following quadratic minimization problem:

This completes the proof of Theorem 3.1.
In Theorem 3.1, if  , then the following corollary can be obtained immediately.
, then the following corollary can be obtained immediately.
Corollary 3.2.
Let  be a real Hilbert space,
be a real Hilbert space,  be a nonempty closed convex subset of
be a nonempty closed convex subset of  ,
,  be an
be an  -inverse strongly monotone mapping and
-inverse strongly monotone mapping and  be a
be a  -inverse strongly monotone mapping. Let
-inverse strongly monotone mapping. Let  be a maximal monotone mapping,
be a maximal monotone mapping,  be a nonexpansive mappings with
be a nonexpansive mappings with  . Let
. Let  be a bifunction satisfying conditions
be a bifunction satisfying conditions  . Let
. Let  be the sequence defined by
be the sequence defined by

where the mapping  is defined by (2.18), and
is defined by (2.18), and  are two constants with
are two constants with  , and
, and

If

where  and GEP are the sets of solutions of variational inclusion (1.2) and generalized equilibrium problem (1.6), then the sequence
and GEP are the sets of solutions of variational inclusion (1.2) and generalized equilibrium problem (1.6), then the sequence  defined by (3.50) converges strongly to
defined by (3.50) converges strongly to  , which is the unique solution of the following quadratic minimization problem:
, which is the unique solution of the following quadratic minimization problem:

In Theorem 3.1, if  , where
, where  is the indicator function of
is the indicator function of  , then the variational inclusion problem (1.2) is equivalent to variational inequality (1.5), that is, to find
, then the variational inclusion problem (1.2) is equivalent to variational inequality (1.5), that is, to find  such that
such that  , for all
, for all  . Since
. Since  . Consequently, we have the following corollary.
. Consequently, we have the following corollary.
Corollary 3.3.
Let  be a real Hilbert space,
be a real Hilbert space,  be a nonempty closed convex subset of
be a nonempty closed convex subset of  ,
,  be an
be an  -inverse strongly monotone mapping and
-inverse strongly monotone mapping and  be a
be a  -inverse strongly monotone mapping. Let
-inverse strongly monotone mapping. Let  and
and  be a nonexpansive mappings with
be a nonexpansive mappings with  . Let
. Let  be a bifunction satisfying conditions
be a bifunction satisfying conditions  . Let
. Let  be the sequence defined by
be the sequence defined by

where the mapping  is defined by (2.18), and
is defined by (2.18), and  are two constants with
are two constants with  , and
, and

If

where  and GEP are the sets of solutions of variational inclusion (1.5) and generalized equilibrium problem (1.6), then the sequence
and GEP are the sets of solutions of variational inclusion (1.5) and generalized equilibrium problem (1.6), then the sequence  defined by (3.54) converges strongly to
defined by (3.54) converges strongly to  , which is the unique solution of the following quadratic minimization problem:
, which is the unique solution of the following quadratic minimization problem:

References
Noor MA, Noor KI: Sensitivity analysis for quasi-variational inclusions. Journal of Mathematical Analysis and Applications 1999,236(2):290–299. 10.1006/jmaa.1999.6424
Chang SS: Set-valued variational inclusions in Banach spaces. Journal of Mathematical Analysis and Applications 2000,248(2):438–454. 10.1006/jmaa.2000.6919
Chang S-S: Existence and approximation of solutions for set-valued variational inclusions in Banach space. Nonlinear Analysis. Theory, Methods & Applications 2001,47(1):583–594. 10.1016/S0362-546X(01)00203-6
Noor MA: Generalized set-valued variational inclusions and resolvent equations. Journal of Mathematical Analysis and Applications 1998,228(1):206–220. 10.1006/jmaa.1998.6127
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Tang F: Strong convergence theorem for a generalized equilibrium problems and a family of infinitely relatively nonexpansive mappings in a Banach space. Acta Analysis Functionalis Applicata 2010,12(3):259–265.
Ceng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. Journal of Computational and Applied Mathematics 2008,214(1):186–201. 10.1016/j.cam.2007.02.022
Li S, Li L, Su Y: General iterative methods for a one-parameter nonexpansive semigroup in Hilbert space. Nonlinear Analysis. Theory, Methods & Applications 2009,70(9):3065–3071. 10.1016/j.na.2008.04.007
Colao V, Marino G, Xu H-K: An iterative method for finding common solutions of equilibrium and fixed point problems. Journal of Mathematical Analysis and Applications 2008,344(1):340–352. 10.1016/j.jmaa.2008.02.041
Zhang S-S, Lee H-W, Chan C-K: Quadratic minimization for equilibrium problem variational inclusion and fixed point problem. Applied Mathematics and Mechanics 2010,31(7):917–928. 10.1007/s10483-010-1326-6
Zhang S-S, Lee JHW, Chan CK: Algorithms of common solutions to quasi variational inclusion and fixed point problems. Applied Mathematics and Mechanics 2008,29(5):571–581. 10.1007/s10483-008-0502-y
Bruck RE Jr.: Properties of fixed-point sets of nonexpansive mappings in Banach spaces. Transactions of the American Mathematical Society 1973, 179: 251–262.
Suzuki T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. Fixed Point Theory and Applications 2005, (1):103–123.
Pascali D: Nonlinear Mappings of Monotone Type. Sijthoff and Noordhoff International Publishers, The Netherlands; 1978.
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Xu H-K: Viscosity approximation methods for nonexpansive mappings. Journal of Mathematical Analysis and Applications 2004,298(1):279–291. 10.1016/j.jmaa.2004.04.059
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tan, J., Chang, S. Iterative Algorithms for Finding Common Solutions to Variational Inclusion Equilibrium and Fixed Point Problems. Fixed Point Theory Appl 2011, 915629 (2011). https://doi.org/10.1155/2011/915629
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/915629
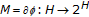 , where
, where  is a proper convex lower semi-continuous function and
is a proper convex lower semi-continuous function and 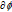 is the subdifferential of
is the subdifferential of  , then the quasivariational inclusion problem (1.2) is equivalent to finding
, then the quasivariational inclusion problem (1.2) is equivalent to finding 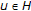 such that
such that 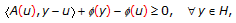
 , where
, where  is a nonempty closed convex subset of
is a nonempty closed convex subset of 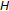 and
and 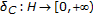 is the indicator function of
is the indicator function of  , that is,
, that is, 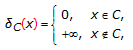
 associated with
associated with 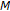 is single-valued and nonexpansive for all
is single-valued and nonexpansive for all  , that is,
, that is, 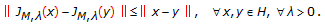
 is a solution of variational inclusion (1.2) if and only if
is a solution of variational inclusion (1.2) if and only if 
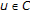 is a solution of generalized equilibrium problem (1.6) if and only if
is a solution of generalized equilibrium problem (1.6) if and only if