- Research Article
- Open access
- Published:
New Iterative Scheme for Finite Families of Equilibrium, Variational Inequality, and Fixed Point Problems in Banach Spaces
Fixed Point Theory and Applications volume 2011, Article number: 372975 (2011)
Abstract
We introduced a new iterative scheme for finding a common element in the set of common fixed points of a finite family of quasi-ϕ-nonexpansive mappings, the set of common solutions of a finite family of equilibrium problems, and the set of common solutions of a finite family of variational inequality problems in Banach spaces. The proof method for the main result is simplified under some new assumptions on the bifunctions.
1. Introduction
Throughout this paper, let  denote the set of all real numbers. Let
denote the set of all real numbers. Let  be a smooth Banach space and
be a smooth Banach space and  the dual space of
the dual space of  . The function
. The function  is defined by
is defined by

where  is the normalized dual mapping from
is the normalized dual mapping from  to
to  defined by
defined by

Let  be a nonempty closed and convex subset of
be a nonempty closed and convex subset of  . The generalized projection
. The generalized projection  is a mapping that assigns to an arbitrary point
is a mapping that assigns to an arbitrary point  the minimum point of the function
the minimum point of the function  , that is,
, that is,  , where
, where  is the solution to the minimization problem
is the solution to the minimization problem

In Hilbert spaces,  and
and  , where
, where  is the metric projection. It is obvious from the definition of function
is the metric projection. It is obvious from the definition of function  that
that

We remark that if  is a reflexive, strictly convex and smooth Banach space, then for
is a reflexive, strictly convex and smooth Banach space, then for  ,
,  if and only if
if and only if  . For more details on
. For more details on  and
and  , the readers are referred to [1–4].
, the readers are referred to [1–4].
Let  be a mapping from
be a mapping from  into itself. We denote the set of fixed points of
into itself. We denote the set of fixed points of  by
by  .
. is called to be nonexpansive if
is called to be nonexpansive if  for all
for all  and quasi-nonexpansive if
and quasi-nonexpansive if  and
and  for all
for all  and
and  . A point
. A point  is called to be an asymptotic fixed point of
is called to be an asymptotic fixed point of  [5] if
[5] if  contains a sequence
contains a sequence  which converges weakly to
which converges weakly to  such that
such that  . The set of asymptotic fixed points of
. The set of asymptotic fixed points of  is denoted by
is denoted by  . The mapping
. The mapping  is said to be relatively nonexpansive [6–8] if
is said to be relatively nonexpansive [6–8] if  and
and  for all
for all  and
and  . The mapping
. The mapping  is said to be
is said to be  -nonexpansive if
-nonexpansive if  for all
for all  .
.  is called to be quasi-
is called to be quasi- -nonexpansive [9] if
-nonexpansive [9] if  and
and  for all
for all  and
and  .
.
In 2005, Matsushita and Takahashi [10] introduced the following algorithm:

where  is the duality mapping on
is the duality mapping on  ,
,  is a relatively nonexpansive mapping from
is a relatively nonexpansive mapping from  into itself, and
into itself, and  is a sequence of real numbers such that
is a sequence of real numbers such that  and
and  and proved that the sequence
and proved that the sequence  generated by (1.5) converges strongly to
generated by (1.5) converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Let  be a bifunction from
be a bifunction from  to
to  . The equilibrium problem for
. The equilibrium problem for  is to find
is to find  such that
such that

We use  to denote the solution set of the equilibrium problem (1.6). That is,
to denote the solution set of the equilibrium problem (1.6). That is,

For studying the equilibrium problem,  is usually assumed to satisfy the following conditions:
is usually assumed to satisfy the following conditions:
(A1) for all
for all  ;
;
(A2) is monotone, that is,
is monotone, that is,  for all
for all  ;
;
(A3)for each  ,
,  ;
;
(A4)for each  ,
,  is convex and lower semicontinuous.
is convex and lower semicontinuous.
Recently, many authors investigated the equilibrium problems in Hilbert spaces or Banach spaces; see, for example, [11–25]. In [20], Qin et al. considered the following iterative scheme by a hybrid method in a Banach space:

where  is a closed quasi-
is a closed quasi- -nonexpansive mapping for each
-nonexpansive mapping for each  ,
,  are real sequences in
are real sequences in  satisfying
satisfying  for each
for each  and
and  for each
for each  and
and  is a real sequence in
is a real sequence in  with
with  . Then the authors proved that
. Then the authors proved that  converges strongly to
converges strongly to  , where
, where  .
.
Very recently, Zegeye and Shahzad [25] introduced a new scheme for finding an element in the common fixed point set of finite family of closed relatively quasi-nonexpansive mappings, common solutions set of finite family of equilibrium problems, and common solutions set of finite family of variational inequality problems for monotone mappings in a Banach space. More precisely, let  ,
,  , be a finite family of bifunctions,
, be a finite family of bifunctions,  ,
,  , a finite family of relatively quasi-nonexpansive mappings, and
, a finite family of relatively quasi-nonexpansive mappings, and  ,
,  , a finite family of continuous monotone mappings. For
, a finite family of continuous monotone mappings. For  , define the mappings
, define the mappings  ,
,  by
by

where  and
and  for some
for some  . Zegeye and Shahzad [25] introduced the following scheme:
. Zegeye and Shahzad [25] introduced the following scheme:

where  ,
,  such that
such that  . Further, they proved that
. Further, they proved that  converges strongly to an element of
converges strongly to an element of  , where
, where  .
.
In this paper, motivated and inspired by the iterations (1.8) and (1.10), we consider a new iterative process with a finite family of quasi- -nonexpansive mappings for a finite family of equilibrium problems and a finite family of variational inequality problems in a Banach space. More precisely, let
-nonexpansive mappings for a finite family of equilibrium problems and a finite family of variational inequality problems in a Banach space. More precisely, let  be a family of quasi-
be a family of quasi- -nonexpansive mappings,
-nonexpansive mappings,  a finite family of bifunctions, and
a finite family of bifunctions, and  a finite family of continuous monotone mappings such that
a finite family of continuous monotone mappings such that  . Let
. Let  and
and  . Define the mappings
. Define the mappings  ,
,  by
by


Consider the iteration

where  are the real numbers in
are the real numbers in  satisfying
satisfying  and for each
and for each  ,
,  are the real numbers in
are the real numbers in  satisfying
satisfying  . We will prove that the sequence
. We will prove that the sequence  generated by (1.13) converges strongly to an element in
generated by (1.13) converges strongly to an element in  . In this paper, in order to simplify the proof, we will replace the condition (A3) with (A3'): for each fixed
. In this paper, in order to simplify the proof, we will replace the condition (A3) with (A3'): for each fixed  ,
,  is continuous.
is continuous.
Obviously, the condition (A3') implies (A3). Under the condition (A3'), we will show that each  (as well as
(as well as  ,
,  ,
,  ) is closed which is such that the proof for the main result of this paper is simplified.
) is closed which is such that the proof for the main result of this paper is simplified.
2. Preliminaries
The modulus of smoothness of a Banach space  is the function
is the function  defined by
defined by

The space  is said to be smooth if
is said to be smooth if  ,
,  , and
, and  is called uniformly smooth if and only if
is called uniformly smooth if and only if  .
.
A Banach space  is said to be strictly convex if
is said to be strictly convex if  for all
for all  with
with  and
and  . It is said to be uniformly convex if
. It is said to be uniformly convex if  for any two sequences
for any two sequences  and
and  in
in  such that
such that  and
and  . It is known that if a Banach space
. It is known that if a Banach space  is uniformly smooth, then its dual space
is uniformly smooth, then its dual space  is uniformly convex.
is uniformly convex.
A Banach space  is called to have the Kadec-Klee property if for any sequence
is called to have the Kadec-Klee property if for any sequence  and
and  with
with  , where
, where  denotes the weak convergence, and
denotes the weak convergence, and  , then
, then  as
as  , where
, where  denotes the strong convergence. It is well known that every uniformly convex Banach space has the Kadec-Klee property. For more details on the Kadec-Klee property, the reader is referred to [3, 4].
denotes the strong convergence. It is well known that every uniformly convex Banach space has the Kadec-Klee property. For more details on the Kadec-Klee property, the reader is referred to [3, 4].
Let  be a nonempty closed and convex subset of a Banach space
be a nonempty closed and convex subset of a Banach space  . A mapping
. A mapping  is said to be closed if for any sequence
is said to be closed if for any sequence  such that
such that  and
and  ,
,  .
.
Let  be a mapping.
be a mapping.  is said to be monotone if for each
is said to be monotone if for each  , the following inequality holds:
, the following inequality holds:

Let  be a monotone mapping from
be a monotone mapping from  into
into  . The variational inequality problem on
. The variational inequality problem on  is formulated as follows:
is formulated as follows:

The solution set of the above variational inequality problem is denoted by  .
.
Next we state some lemmas which will be used later.
Lemma 2.1 (see [1]).
Let  be a nonempty closed and convex subset of a smooth Banach space
be a nonempty closed and convex subset of a smooth Banach space  and
and  . Then,
. Then,  if and only if
if and only if

Lemma 2.2 (see [1]).
Let  be a reflexive, strictly convex and smooth Banach space,
be a reflexive, strictly convex and smooth Banach space,  a nonempty closed and convex subset of
a nonempty closed and convex subset of  , and
, and  . Then
. Then

Lemma 2.3 (see [20]).
Let  be a strictly convex and smooth Banach space,
be a strictly convex and smooth Banach space,  a nonempty closed and convex subset of
a nonempty closed and convex subset of  , and
, and  a quasi-
a quasi- -nonexpansive mapping. Then
-nonexpansive mapping. Then  is a closed and convex subset of
is a closed and convex subset of  .
.
Since the condition (A3') implies (A3), the following lemma is a natural result of [22, Lemmas 2.8 and 2.9].
Lemma 2.4.
Let  be a closed and convex subset of a smooth, strictly convex and reflexive Banach space
be a closed and convex subset of a smooth, strictly convex and reflexive Banach space  . Let
. Let  be a bifunction from
be a bifunction from  satisfying (A1), (A2), (A3'), and (A4). Let
satisfying (A1), (A2), (A3'), and (A4). Let  and
and  . Then
. Then
-
(a)
there exists
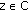 such that
such that

-
(b)
define a mapping
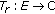 by
by

Then the following conclusions hold:
(1) is single-valued;
is single-valued;
(2) is firmly nonexpansive, that is, for all
is firmly nonexpansive, that is, for all  ,
,

(3) ;
;
(4) is quasi-
is quasi- -nonexpansive;
-nonexpansive;
(5) is closed and convex;
is closed and convex;
(6) .
.
Remark 2.5.
Let  be a continuous monotone mapping and define
be a continuous monotone mapping and define  for all
for all  . It is easy to see that
. It is easy to see that  satisfies the conditions (A1), (A2), (A3'), and (A4) and
satisfies the conditions (A1), (A2), (A3'), and (A4) and  . Hence, for every real number
. Hence, for every real number  , if defining a mapping
, if defining a mapping  by
by

then  satisfies all the conclusions in Lemma 2.4. See [25, Lemma 2.4].
satisfies all the conclusions in Lemma 2.4. See [25, Lemma 2.4].
Lemma 2.6 (see [26]).
Let  and
and  be two fixed real numbers. Then a Banach space
be two fixed real numbers. Then a Banach space  is uniformly convex if and only if there exists a continuous strictly increasing convex function
is uniformly convex if and only if there exists a continuous strictly increasing convex function  with
with  such that
such that

for all  and
and  , where
, where  .
.
The following lemma can be obtained from Lemma 2.6 immediately; also see [20, Lemma 1.9].
Lemma 2.7 (see [20]).
Let  be a uniformly convex Banach space,
be a uniformly convex Banach space,  a positive number, and
a positive number, and  a closed ball of
a closed ball of  . There exists a continuous, strictly increasing and convex function
. There exists a continuous, strictly increasing and convex function  with
with  such that
such that

for all  and
and  such that
such that  .
.
Lemma 2.8.
Let  be a closed and convex subset of a uniformly smooth and strictly convex Banach space
be a closed and convex subset of a uniformly smooth and strictly convex Banach space  . Let
. Let  be a bifunction satisfying (A1), (A2), (A3'), and (A4). Let
be a bifunction satisfying (A1), (A2), (A3'), and (A4). Let  and
and  be a mapping defined by (2.7). Then Tr is closed.
be a mapping defined by (2.7). Then Tr is closed.
Proof.
Let  converge to
converge to  and
and  converge to
converge to  . To end the conclusion, we need to prove that
. To end the conclusion, we need to prove that  . Indeed, for each
. Indeed, for each  , Lemma 2.4 shows that there exists a unique
, Lemma 2.4 shows that there exists a unique  such that
such that  , that is,
, that is,

Since  is uniformly smooth,
is uniformly smooth,  is continuous on bounded set (note that
is continuous on bounded set (note that  and
and  are both bounded). Taking the limit as
are both bounded). Taking the limit as  in (2.12), by using (A3'), we get
in (2.12), by using (A3'), we get

which implies that  . This completes the proof.
. This completes the proof.
3. Main Results
Theorem 3.1.
Let  be a nonempty closed and convex subset of a uniformly smooth and strictly convex Banach space
be a nonempty closed and convex subset of a uniformly smooth and strictly convex Banach space  which has the Kadec-Klee property. Let
which has the Kadec-Klee property. Let  be a family of closed quasi-
be a family of closed quasi- -nonexpansive mappings,
-nonexpansive mappings,  a finite family of bifunctions satisfying the conditions (A1), (A2), (A3'), and (A4), and
a finite family of bifunctions satisfying the conditions (A1), (A2), (A3'), and (A4), and  a finite family of continuous monotone mappings such that
a finite family of continuous monotone mappings such that  . Let
. Let  . Let
. Let  be a sequence generated by the following manner:
be a sequence generated by the following manner:

where 
 and
and 
 are defined by (1.11) and (1.12),
are defined by (1.11) and (1.12),  are the real numbers in
are the real numbers in  satisfying
satisfying  and for each
and for each  ,
,  are the real numbers in
are the real numbers in  satisfying
satisfying  . Then the sequence
. Then the sequence  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Proof.
First we prove that  is closed and convex for each
is closed and convex for each  . From the definition of
. From the definition of  , it is obvious that
, it is obvious that  is closed. Moreover, since
is closed. Moreover, since  is equivalent to
is equivalent to  , it follows that
, it follows that  is convex for each
is convex for each  . By the definition of
. By the definition of  , we can conclude that
, we can conclude that  is closed and convex for each
is closed and convex for each  .
.
Next, we prove that  for each
for each  . From Lemma 2.4 and Remark 2.5, we see that each
. From Lemma 2.4 and Remark 2.5, we see that each  (
( ) and
) and  (
( ) are quasi-
) are quasi- -nonexpansive. Hence, for any
-nonexpansive. Hence, for any  , we have
, we have

which implies that  for each
for each  . So, it follows from the definition of
. So, it follows from the definition of  that
that  for each
for each  . Therefore, the sequence
. Therefore, the sequence  is well defined. Also, from Lemma 2.2 we see that
is well defined. Also, from Lemma 2.2 we see that

for each  . This shows that the sequence
. This shows that the sequence  is bounded. It follows from (1.4) that the sequence
is bounded. It follows from (1.4) that the sequence  is also bounded.
is also bounded.
Since  is reflexive, we may, without loss of generality, assume that
is reflexive, we may, without loss of generality, assume that  . Since
. Since  is closed and convex for each
is closed and convex for each  , we can conclude that
, we can conclude that  for each
for each  . By the definition of
. By the definition of  , we see that
, we see that

It follows that

This implies that

Hence, we have  as
as  . In view of the Kadec-Klee property of
. In view of the Kadec-Klee property of  , we get that
, we get that

By the construction of  , we have that
, we have that  and
and  . It follows from Lemma 2.2 that
. It follows from Lemma 2.2 that

Letting  , we obtain that
, we obtain that  . In view of
. In view of  , we have
, we have  and hence
and hence

It follows that

From (1.4), we see that

Hence,

This implies that the sequence  is bounded. Note that reflexivity of
is bounded. Note that reflexivity of  implies reflexivity of
implies reflexivity of  . Thus, we may assume that
. Thus, we may assume that  . Furthermore, reflexivity of
. Furthermore, reflexivity of  implies that there exists
implies that there exists  such that
such that  . Then, it follows that
. Then, it follows that

Take  on both sides of (3.13) over
on both sides of (3.13) over  and use weak lower semicontinuity of norm to get that
and use weak lower semicontinuity of norm to get that

which implies that  . Hence,
. Hence,  . It follows that
. It follows that  . Now, from (3.12) and Kadec-Klee property of
. Now, from (3.12) and Kadec-Klee property of  , we obtain that
, we obtain that  as
as  . Then the demicontinuity of
. Then the demicontinuity of  implies that
implies that  . Now, from (3.11) and the fact that
. Now, from (3.11) and the fact that  has the Kadec-Klee property, we obtain that
has the Kadec-Klee property, we obtain that  . Note that
. Note that

It follows that

Since  is uniformly norm-to-norm continuous on any bounded sets, we have
is uniformly norm-to-norm continuous on any bounded sets, we have

Since  is uniformly smooth, we know that
is uniformly smooth, we know that  is uniformly convex. In view of Lemma 2.7, we see that, for any
is uniformly convex. In view of Lemma 2.7, we see that, for any  ,
,

It follows that

Note that

It follows from (3.16) and (3.17) that

By (3.19), (3.21), and  , we have
, we have

It follows from the property of  that
that

Since  as
as  and
and  is demicontinuous, we obtain that
is demicontinuous, we obtain that  . Note that
. Note that

This implies that

Since  enjoys the Kadec-Klee property, we see that
enjoys the Kadec-Klee property, we see that

Note that

From (3.23) and (3.26), we arrive at

Note that  is demicontinuous. It follows that
is demicontinuous. It follows that  . On the other hand, since
. On the other hand, since

by (3.28) we conclude that  as
as  . Since
. Since  enjoys the Kadec-Klee property, we obtain that
enjoys the Kadec-Klee property, we obtain that

By repeating (3.18)–(3.30), we also can get



Since each  is closed, by (3.30) and (3.31) we conclude that
is closed, by (3.30) and (3.31) we conclude that  , that is,
, that is,  ,
,  . On the other hand, Lemma 2.4, Remark 2.5, and Lemma 2.8 show that
. On the other hand, Lemma 2.4, Remark 2.5, and Lemma 2.8 show that 
 and
and 
 are closed. So, by (3.32) and (3.33) we have
are closed. So, by (3.32) and (3.33) we have 
 and
and 
 . Now, it follows from Lemma 2.4 and Remark 2.5 that
. Now, it follows from Lemma 2.4 and Remark 2.5 that  (
( ) and
) and  (
( ). Hence,
). Hence,  (
( ) and
) and  (
( ). Therefore,
). Therefore,  .
.
Finally, we prove that  . From
. From  , by Lemma 2.1, we see that
, by Lemma 2.1, we see that

Since  for each
for each  , we have
, we have

Letting  in (3.35), we see that
in (3.35), we see that

In view of Lemma 2.1, we can obtain that  . This completes the proof.
. This completes the proof.
Remark 3.2.
Obviously, the proof process of  is simple since we replace the condition (A3) with (A3') which is such that
is simple since we replace the condition (A3) with (A3') which is such that  and
and 
 are closed. In fact, although the condition (A3') is stronger than (A3), it is not easier to verify the condition (A3) than verify the condition (A3'). Hence, from this point, the condition (A3') is acceptable. On the other hand, the definition of
are closed. In fact, although the condition (A3') is stronger than (A3), it is not easier to verify the condition (A3) than verify the condition (A3'). Hence, from this point, the condition (A3') is acceptable. On the other hand, the definition of  is of some interest.
is of some interest.
If  for each
for each  ,
,  for each
for each  and
and  for each
for each  , then Theorem 3.1 reduces to the following result.
, then Theorem 3.1 reduces to the following result.
Corollary 3.3.
Let  be a nonempty closed and convex subset of a uniformly smooth and strictly convex Banach space
be a nonempty closed and convex subset of a uniformly smooth and strictly convex Banach space  which has the Kadec-Klee property. Let
which has the Kadec-Klee property. Let  be a closed quasi-
be a closed quasi- -nonexpansive mapping,
-nonexpansive mapping,  a bifunction satisfying the conditions (A1), (A2), (A3'), and (A4) and
a bifunction satisfying the conditions (A1), (A2), (A3'), and (A4) and  a continuous monotone mapping such that
a continuous monotone mapping such that  . Let
. Let  . Let
. Let  be a sequence defined by the following manner:
be a sequence defined by the following manner:

where  and
and  are defined by (1.11) and (1.12) with
are defined by (1.11) and (1.12) with 
 and
and 
 ,
,  are the real numbers in
are the real numbers in  satisfying
satisfying  . Then the sequence
. Then the sequence  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Corollary 3.4.
Let  be a nonempty closed and convex subset of a Hilbert space
be a nonempty closed and convex subset of a Hilbert space  . Let
. Let  be a family of closed quasi-nonexpansive mappings,
be a family of closed quasi-nonexpansive mappings,  a finite family of bifunctions satisfying the conditions (A1)–(A4), and
a finite family of bifunctions satisfying the conditions (A1)–(A4), and  a finite family of continuous monotone mappings such that
a finite family of continuous monotone mappings such that  . Let
. Let  . Define a sequence
. Define a sequence  by the following manner:
by the following manner:

where  and
and  are defined by (1.11) and (1.12) with
are defined by (1.11) and (1.12) with  (
( is the identity mapping),
is the identity mapping),  are the real numbers in
are the real numbers in  satisfying
satisfying  and for each
and for each  ,
,  are the real numbers in
are the real numbers in  satisfying
satisfying  . Then the sequence
. Then the sequence  converges strongly to
converges strongly to  , where
, where  is the projection from
is the projection from  onto
onto  .
.
Proof.
By the proof of Theorem 3.1, we have  as
as  ,
,

Since each  is closed, we can conclude that
is closed, we can conclude that  ,
,  . Note that in a Hilbert space, a firmly-nonexpansive mapping is also nonexpansive. Hence,
. Note that in a Hilbert space, a firmly-nonexpansive mapping is also nonexpansive. Hence,  and
and  are nonexpansive for each
are nonexpansive for each  and
and  . By demiclosed principle, we can conclude that
. By demiclosed principle, we can conclude that  and
and  for each
for each  and
and  . That is,
. That is,  . Then by the final part of proof of Theorem 3.1, we have
. Then by the final part of proof of Theorem 3.1, we have  . This completes the proof.
. This completes the proof.
Let  be a Hilbert space and
be a Hilbert space and  a nonempty closed and convex subset of
a nonempty closed and convex subset of  . A mapping
. A mapping  is called a pseudocontraction if for all
is called a pseudocontraction if for all  ,
,

or equivalently,

Let  , where
, where  is a pseudocontraction. Then
is a pseudocontraction. Then  is a monotone mapping and
is a monotone mapping and  . Moreover,
. Moreover,  . Indeed, it is easy to see that
. Indeed, it is easy to see that  . Let
. Let  . We have
. We have

for all  . Take
. Take  . Then we have
. Then we have  . That is,
. That is,  . This shows that
. This shows that  , which implies that
, which implies that  . So,
. So,  . Based this, we have following result.
. Based this, we have following result.
Corollary 3.5.
Let  be a nonempty closed and convex subset of a Hilbert space
be a nonempty closed and convex subset of a Hilbert space  . Let
. Let  be a family of closed quasi-nonexpansive mappings,
be a family of closed quasi-nonexpansive mappings,  a finite family of bifunctions satisfying the conditions (A1)–(A4), and
a finite family of bifunctions satisfying the conditions (A1)–(A4), and  a finite family of continuous pseudocontractions such that
a finite family of continuous pseudocontractions such that  . Let
. Let  . Define a sequence
. Define a sequence  by the following manner:
by the following manner:

where  are defined by (1.11) with
are defined by (1.11) with  and
and  is defined by
is defined by

 are the real numbers in
are the real numbers in  satisfying
satisfying  and for each
and for each  ,
,  are the real numbers in
are the real numbers in  satisfying
satisfying  . Then the sequence
. Then the sequence  converges strongly to
converges strongly to  , where
, where  is the projection from
is the projection from  onto
onto  .
.
If  ,
,  , and
, and  for each
for each  ,
,  , and
, and  , then Corollary 3.5 reduced the following result.
, then Corollary 3.5 reduced the following result.
Corollary 3.6.
Let  be a nonempty closed and convex subset of a Hilbert space
be a nonempty closed and convex subset of a Hilbert space  . Let
. Let  be a closed quasi-nonexpansive mapping,
be a closed quasi-nonexpansive mapping,  a bifunction satisfying the conditions (A1)–(A4), and
a bifunction satisfying the conditions (A1)–(A4), and  a continuous pseudocontraction such that
a continuous pseudocontraction such that  . Let
. Let  . Define a sequence
. Define a sequence  by the following manner:
by the following manner:

where  is defined by (1.11) with
is defined by (1.11) with  and
and  ,
,  is defined by (3.44)
is defined by (3.44)  , and
, and  are the real numbers in
are the real numbers in  satisfying
satisfying  . Then the sequence
. Then the sequence  converges strongly to
converges strongly to  , where
, where  is the projection from
is the projection from  onto
onto  .
.
References
Alber YI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Appl. Math.. Volume 178. Dekker, New York, NY, USA; 1996:15–50.
Alber YaI, Reich S: An iterative method for solving a class of nonlinear operator equations in Banach spaces. Panamerican Mathematical Journal 1994,4(2):39–54.
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Mathematics and Its Applications. Volume 62. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990:xiv+260.
Takahashi W: Nonlinear Functional Analysis. Yokohama Publishers, Yokohama, Japan; 2000:iv+276. Fixed point theory and Its application
Reich S: A weak convergence theorem for the alternating method with Bregman distances. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Appl. Math.. Volume 178. Edited by: Kartsatos AG. Dekker, New York, NY, USA; 1996:313–318.
Butnariu D, Reich S, Zaslavski AJ: Asymptotic behavior of relatively nonexpansive operators in Banach spaces. Journal of Applied Analysis 2001,7(2):151–174. 10.1515/JAA.2001.151
Butnariu D, Reich S, Zaslavski AJ: Weak convergence of orbits of nonlinear operators in reflexive Banach spaces. Numerical Functional Analysis and Optimization 2003,24(5–6):489–508. 10.1081/NFA-120023869
Censor Y, Reich S: Iterations of paracontractions and firmly nonexpansive operators with applications to feasibility and optimization. Optimization 1996,37(4):323–339. 10.1080/02331939608844225
Zhou H, Gao G, Tan B: Convergence theorems of a modified hybrid algorithm for a family of quasi- ϕ -asymptotically nonexpansive mappings. Journal of Applied Mathematics and Computing 2010,32(2):453–464. 10.1007/s12190-009-0263-4
Matsushita S-y, Takahashi W: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. Journal of Approximation Theory 2005,134(2):257–266. 10.1016/j.jat.2005.02.007
Ceng L-C, Yao J-C: Hybrid viscosity approximation schemes for equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Applied Mathematics and Computation 2008,198(2):729–741. 10.1016/j.amc.2007.09.011
Ceng L-C, Al-Homidan S, Ansari QH, Yao J-C: An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings. Journal of Computational and Applied Mathematics 2009,223(2):967–974. 10.1016/j.cam.2008.03.032
Ceng LC, Petruşel A, Yao JC: Iterative approaches to solving equilibrium problems and fixed point problems of infinitely many nonexpansive mappings. Journal of Optimization Theory and Applications 2009,143(1):37–58. 10.1007/s10957-009-9549-9
Chang S-S, Cho YJ, Kim JK: Approximation methods of solutions for equilibrium problem in Hilbert spaces. Dynamic Systems and Applications 2008,17(3–4):503–513.
Chang S-S, Joseph Lee HW, Chan CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Analysis: Theory, Methods & Applications 2009,70(9):3307–3319. 10.1016/j.na.2008.04.035
Kumam P, Katchang P: A viscosity of extragradient approximation method for finding equilibrium problems, variational inequalities and fixed point problems for nonexpansive mappings. Nonlinear Analysis: Hybrid Systems 2009,3(4):475–486. 10.1016/j.nahs.2009.03.006
Moudafi A: Weak convergence theorems for nonexpansive mappings and equilibrium problems. Journal of Nonlinear and Convex Analysis 2008,9(1):37–43.
Plubtieng S, Punpaeng R: A new iterative method for equilibrium problems and fixed point problems of nonexpansive mappings and monotone mappings. Applied Mathematics and Computation 2008,197(2):548–558. 10.1016/j.amc.2007.07.075
Qin X, Cho YJ, Kang SM: Viscosity approximation methods for generalized equilibrium problems and fixed point problems with applications. Nonlinear Analysis: Theory, Methods & Applications 2010,72(1):99–112. 10.1016/j.na.2009.06.042
Qin X, Cho SY, Kang SM: Strong convergence of shrinking projection methods for quasi- ϕ -nonexpansive mappings and equilibrium problems. Journal of Computational and Applied Mathematics 2010,234(3):750–760. 10.1016/j.cam.2010.01.015
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,331(1):506–515. 10.1016/j.jmaa.2006.08.036
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(1):45–57. 10.1016/j.na.2007.11.031
Wang S, Marino G, Wang F: Strong convergence theorems for a generalized equilibrium problem with a relaxed monotone mapping and a countable family of nonexpansive mappings in a Hilbert space. Fixed Point Theory and Applications 2010, 2010:-22.
Cho YJ, Wang S, Qin X: A new iterative method for solving equilibrium problems and fixed point problems for infinite family of nonexpansive mappings. Fixed Point Theory and Applications 2010, 2010:-18.
Zegeye H, Shahzad N: A hybrid scheme for finite families of equilibrium, variational inequality and fixed point problems. Nonlinear Analysis: Theory, Methods & Applications 2011,74(1):263–272. 10.1016/j.na.2010.08.040
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Acknowledgment
This work was supported by the Natural Science Foundation of Hebei Province (A2010001482).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, S., Zhou, C. New Iterative Scheme for Finite Families of Equilibrium, Variational Inequality, and Fixed Point Problems in Banach Spaces. Fixed Point Theory Appl 2011, 372975 (2011). https://doi.org/10.1155/2011/372975
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/372975
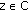 such that
such that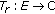 by
by