- Research Article
- Open access
- Published:
Fixed Points of Discontinuous Multivalued Operators in Ordered Spaces with Applications
Fixed Point Theory and Applications volume 2010, Article number: 745769 (2010)
Abstract
Existence theorems of fixed points for multivalued increasing operators in partially ordered spaces are presented. Here neither the continuity nor compactness is assumed for multivalued operators. As an application, we lead to the existence principles for integral inclusions of Hammerstein type multivalued maps.
1. Introduction
The influence of fixed point theorems for contractive and nonexpansive mappings (see [1, 2]) on fixed point theory is so huge that there are many results dealing with fixed points of mappings satisfying various types of contractive and nonexpansive conditions. On the other hand, it is also huge that well-known Brouwer's and Schauder's fixed point theorems for set-contractive mappings exert an influence on this theory. However, if a mapping is not completely continuous, in general, it is difficult to verify that the mapping satisfies the set-contractive condition. In 1980, Mönch [3] has obtained the following important fixed point theorem which avoids the above mentioned difficulty.
Theorem 1.1.
Let  be a Banach space,
be a Banach space,  a closed convex subset. Suppose that (single) operator
a closed convex subset. Suppose that (single) operator  is continuous and satisfies that
is continuous and satisfies that
(i)there exists  such that if
such that if  is countable, then
is countable, then  is relatively compact,
is relatively compact,
then  has a fixed point in
has a fixed point in  .
.
It has been observed that continuity is an ideal and important property in the above cited works, while in some applications the mapping under consideration may not be continuous, yet at the same time it may be "not very discontinuous". this idea has motivated many authors to study corresponding problems, for instance, the stability of Brouwer's fixed point theorem [4], similar result for nonexpansive mappings [5], and existence and approximation of the synthetic approaches to fixed point theorems [6]. Recently, fixed point theory for discontinuous multivalued mappings has attracted much attention and many authors studied the existence of fixed points for such mappings. We refer to [7–11]. For example, Hong [8] has extended Mönch [3] to discontinuous multivalued operators in ordered Banach spaces by using a quite weak compactness condition; that is, assuming the following condition is satisfied.
(H)If  is a countable totally ordered set and
is a countable totally ordered set and  , then
, then  is weakly relatively compact. Here
is weakly relatively compact. Here  is a multivalued operator and
is a multivalued operator and  denotes the weak closure of the set
denotes the weak closure of the set  .
.
The purpose of this paper is to present some results on fixed point theorems of Mönch type of multivalued increasing operators for which neither the continuity nor the compactness is assumed in ordered topological spaces. However, we will use the following hypothesis.
(H1)If  is a countable totally ordered set and
is a countable totally ordered set and  , then
, then  has a supremum.
has a supremum.
 is a topological vector space endowed with partial ordering "
is a topological vector space endowed with partial ordering " ",
",  stands for the closure of the set
stands for the closure of the set  , and
, and  with
with  is a given ordered set of
is a given ordered set of  .
.
This paper is organized as follows. In Section 2, we introduce some definitions and preliminary facts from partially ordered theory and multivalued analysis which are used later. In especial, we introduce a new partial ordering of sets which forms a basis to our main results. In Section 3, we state and prove existence of fixed points, also, maximal and minimal fixed point theorem is presented for discontinuous multivalued increasing operators which are our main results. To illustrate the applicability of our theory, in Section 4, we discuss the existence of solutions to the Hammerstein integral inclusions of the form

2. Preliminaries
Let  be a partially ordered topological vector space. By the notation "
be a partially ordered topological vector space. By the notation " " we always mean that
" we always mean that  and
and  . Let
. Let  stand for the collection of all nonempty subsets of
stand for the collection of all nonempty subsets of  . Take
. Take  and let
and let  be a given ordered set of
be a given ordered set of  . The ordered interval of
. The ordered interval of  is written as
is written as  .
.
For two subsets  of
of  , we write
, we write  (or
(or  ) if
) if

Given a nonempty subsets  of
of  we say that
we say that  is increasing upwards if
is increasing upwards if  ,
,  , and
, and  imply that there exists
imply that there exists  such that
such that  .
.  is increasing downwards if
is increasing downwards if  ,
,  , and
, and  imply an existence of
imply an existence of  such that
such that  . If
. If  is increasing upwards and downwards we say that
is increasing upwards and downwards we say that  is increasing.
is increasing.
Let  be nonempty. The element
be nonempty. The element  is called an upper (lower) bound of
is called an upper (lower) bound of  if
if  (
( ) whenever
) whenever  .
.  is called upper (lower) bounded with respect to the ordering if its upper (lower) bounds exist. The element
is called upper (lower) bounded with respect to the ordering if its upper (lower) bounds exist. The element  is called a supremum of
is called a supremum of  , written as
, written as  , if
, if  is an upper bound and
is an upper bound and  as long as
as long as  is another upper bound of
is another upper bound of  . Similarly, we can define the infimum
. Similarly, we can define the infimum  of
of  .
.
Throughout this paper, unless otherwise mentioned, the partial ordering of  always introduced by a closed cone if
always introduced by a closed cone if  is a Banach space. The following lemmas will be used in after sections.
is a Banach space. The following lemmas will be used in after sections.
Lemma 2.1 (see [12]).
Let  be an ordered Banach space and
be an ordered Banach space and  a totally ordered and weakly relatively compact subset of
a totally ordered and weakly relatively compact subset of  , then there exists
, then there exists  such that
such that  foe all
foe all  .
.
An ordered topological vector space  is said to have the limit ordinal property if
is said to have the limit ordinal property if  with
with  for
for  , and
, and  for
for  imply
imply  . By an analogy of the proof of Lemma 1.1.2 in [12], we have the following.
. By an analogy of the proof of Lemma 1.1.2 in [12], we have the following.
Lemma 2.2.
If  has the limit ordinal property and
has the limit ordinal property and  is a relatively compact monotone sequence of
is a relatively compact monotone sequence of  , then
, then  is convergent. Moreover,
is convergent. Moreover,  if
if  is increasing and
is increasing and  if
if  is decreasing for
is decreasing for  Here
Here  .
.
Remark 2.3.
Under the assumptions of Lemma 2.2, it is evident that  is the supremum (infimum) of increasing (decreasing) sequence
is the supremum (infimum) of increasing (decreasing) sequence  .
.
Lemma 2.4.
Let the increasing sequence  have the supremum
have the supremum  . If
. If  is a infinity subsequence of
is a infinity subsequence of  , then
, then  has the supremum
has the supremum  , too.
, too.
Proof.
Evidently,  is an upper bound of
is an upper bound of  . Let
. Let  be the other one, then
be the other one, then  for
for  For any given
For any given  , since
, since  is infinity, there exists
is infinity, there exists  such that
such that  , which implies that
, which implies that  for all
for all  . From the definition of supremums it follows that
. From the definition of supremums it follows that  , that is,
, that is,  is the supremum of
is the supremum of  .
.
Lemma 2.5.
Suppose that every countable totally ordered subset of the partially ordered set  has a supremum in
has a supremum in  . Let the operator
. Let the operator  satisfy
satisfy  for all
for all  , then there exists
, then there exists  such that
such that  .
.
Proof.
Take  any fixed and let
any fixed and let  for
for  , then
, then  that is,
that is,  is increasing. From our assumption it follows that
is increasing. From our assumption it follows that  has a supremum denoted by
has a supremum denoted by  . Let
. Let

If  , then the conclusion of the lemma is proved. Otherwise, take
, then the conclusion of the lemma is proved. Otherwise, take  for
for  Again, the set
Again, the set  has the supremum
has the supremum  . Denote
. Denote  . If
. If  , then the conclusion of the lemma is proved. Otherwise, take
, then the conclusion of the lemma is proved. Otherwise, take  for
for  , and let
, and let  with
with  . In general, having defined
. In general, having defined  with
with  and
and  , where
, where  and
and  , if
, if  , which completes the proof. Otherwise, repeating this process, either the conclusion of the lemma is proved, or we can obtain a set sequence
, which completes the proof. Otherwise, repeating this process, either the conclusion of the lemma is proved, or we can obtain a set sequence  satisfying
satisfying
(i) with
with  and
and  ,
,  ;
;
(ii) for
for  ;
;
(iii)
 , and
, and  .
.
Let  , then
, then  is a countable subset and
is a countable subset and

We claim that

In fact, for any  , there exists
, there exists  such that
such that  . There exists
. There exists  such that
such that  . If
. If  for some nature number
for some nature number  , then
, then  which yields
which yields  . Otherwise, we have
. Otherwise, we have  . This implies that
. This implies that  . Consequently,
. Consequently,  . From the arbitrariness of
. From the arbitrariness of  it follows that (2.4) is satisfied.
it follows that (2.4) is satisfied.
Finally, combining  and
and  we see easily that
we see easily that  is totally ordered. Our hypothesis guarantees that
is totally ordered. Our hypothesis guarantees that  has a supremum, written as
has a supremum, written as  . Note that (2.4) guarantees
. Note that (2.4) guarantees  , we have
, we have  . On the other hand, the definition of
. On the other hand, the definition of  ensures that
ensures that  . Hence
. Hence  . This proof is completed.
. This proof is completed.
Let  be a nonempty subset of
be a nonempty subset of  . In this section we impose the following hypotheses on the increasing upwards multivalued operator
. In this section we impose the following hypotheses on the increasing upwards multivalued operator  . Set
. Set

and for any  define that
define that

where,  and
and  is given as follows: since
is given as follows: since  , there exists
, there exists  such that
such that  . In virtue of the fact that
. In virtue of the fact that  is increasing upwards, there exists
is increasing upwards, there exists  such that
such that  . On the analogy of this process, there exists
. On the analogy of this process, there exists  such that
such that  for
for  Obviously,
Obviously,  , thus, the condition (H1) guarantees that the supremum
, thus, the condition (H1) guarantees that the supremum  of
of  exists.
exists.
Remark 2.6.
In general, the sequences of these kinds,  , may not be unique, that is, every
, may not be unique, that is, every  corresponds to
corresponds to  , moreover, corresponds to
, moreover, corresponds to  . For given
. For given  , we denote with
, we denote with  and
and  the families of
the families of  and
and  as above, respectively.
as above, respectively.
In addition, if  has the limit ordinal property,
has the limit ordinal property,  is a closed set for any
is a closed set for any  . In fact, let
. In fact, let  be any infinity subsequence of
be any infinity subsequence of  for which
for which

observing that  is increasing, by Lemma 2.2 we get that
is increasing, by Lemma 2.2 we get that  is a supremum of
is a supremum of  and by Lemma 2.4 we get
and by Lemma 2.4 we get  .
.
Definition 2.7.
A set  is said to be sup-closed if the supremum of each countable subset of
is said to be sup-closed if the supremum of each countable subset of  (provided that it exists) belongs to
(provided that it exists) belongs to  . A multivalued operator
. A multivalued operator  is said to have sup-closed values if
is said to have sup-closed values if  is sup-closed for each
is sup-closed for each  .
.
Defining

Lemma 2.8.
Let  be an ordered topological space,
be an ordered topological space,  a nonempty subset of
a nonempty subset of  with
with  ; let
; let  have sup-closed values and satisfy hypothesis (H1). Moreover, assume that
have sup-closed values and satisfy hypothesis (H1). Moreover, assume that
(H2) is increasing upwards and satisfies
is increasing upwards and satisfies  ,
,
then for any  ,
,  has the supremum
has the supremum  which belongs to
which belongs to  that is,
that is,

Proof.
It is clear that  has the supremum
has the supremum  . For any
. For any  , from
, from  and
and  there exists
there exists  such that
such that  . We can assume that the sequence
. We can assume that the sequence  is increasing. Indeed, if
is increasing. Indeed, if  for
for  , our purpose is reached. Otherwise, there exists
, our purpose is reached. Otherwise, there exists  such that
such that  , then we take
, then we take  instead of
instead of  . Let
. Let  , then
, then  . Condition (H1) guarantees that
. Condition (H1) guarantees that  has a supremum
has a supremum  . Clearly,
. Clearly,  . By virtue of the fact that
. By virtue of the fact that  has sup-closed values, we have
has sup-closed values, we have  . This proof is complete.
. This proof is complete.
For the sake of convenience, in this paper, by  we always stand for the supremum of
we always stand for the supremum of  . For given
. For given  , let
, let  be a set consisting of all
be a set consisting of all  given as in Lemma 2.8, then
given as in Lemma 2.8, then  is an increasing map. Now for any
is an increasing map. Now for any  Lemma 2.4 shows
Lemma 2.4 shows  , thus,
, thus,  . Define
. Define

It is obvious that  . Hence,
. Hence,  is nonempty. A relation
is nonempty. A relation  on Z is defined as follows (it is easy to see that
on Z is defined as follows (it is easy to see that  is a partially ordered set):
is a partially ordered set):
 ;
;
 and
and  .
.
Remark 2.9.
It is clear we may assume that, for any  , there exists
, there exists  such that
such that  if
if  .
.
Let us assume that there exists some  such that
such that
(H3) .
.
Define

Obviously,  , that is,
, that is,  is nonempty if
is nonempty if  is increasing upwards. Now we denote
is increasing upwards. Now we denote  as a relation on
as a relation on  defined by, for any
defined by, for any  ,
,
(I)
(II) , there exists
, there exists  such that
such that  and
and
(b)there exists a countable at most and totally ordered subset  such that
such that
() for any
for any  .
.
() There exists  such that
such that

() is a totally ordered set and satisfies
is a totally ordered set and satisfies  .
.  is called a link of linking
is called a link of linking  with
with  .
.
Remark 2.10.
( ) may be satisfied. In fact, we can take empty set as a link of linking
) may be satisfied. In fact, we can take empty set as a link of linking  and
and  . Thus,
. Thus,  implies that for any
implies that for any  we can find
we can find  such that
such that  . In this case, we take
. In this case, we take  . Besides,
. Besides,  can be a finite set, for example,
can be a finite set, for example,  with
with  then
then  . (
. ( ) and the condition (H1) ensure
) and the condition (H1) ensure  to exist the supremum, so, from Lemma 2.2 the element
to exist the supremum, so, from Lemma 2.2 the element  satisfying (
satisfying ( ) exists.
) exists.
Lemma 2.11.
The relation " " satisfies that
" satisfies that
(i) ;
;
(ii) and
and  implies
implies  ;
;
(iii) implies
implies  .
.
Therefore,  is a partially ordered set.
is a partially ordered set.
Proof.
-
(i)
and (ii) are satisfied. Trivial by (I) and (II)(a). To prove (iii), for any given
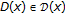 we take
we take 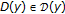 such that
such that 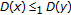 and we can find
and we can find  such that
such that 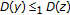 . It is sufficient to assume that at least one of the above equalities does not hold. The definition of
. It is sufficient to assume that at least one of the above equalities does not hold. The definition of  guarantees that
guarantees that 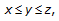 (2.13)
(2.13)

and at least one strictly inequality in (2.13) holds. The links linking  with
with  and linking
and linking  with
with  are written, respectively, as
are written, respectively, as  and
and  . Let
. Let  , for any
, for any  , if none of equalities in (2.13) holds, then by (b
, if none of equalities in (2.13) holds, then by (b ) we have
) we have

If at least one equality in (2.13) holds, for instance,  , then (b
, then (b ) and (b
) and (b ) show that
) show that

Hence,  is a countable totally ordered subset and satisfies (b
is a countable totally ordered subset and satisfies (b ).
).
Next we will prove that  satisfies (b
satisfies (b ). It is clear that the following consequences are true, that is,
). It is clear that the following consequences are true, that is,  and
and  . It is easy to see that
. It is easy to see that  for all
for all  by
by  and
and  for all
for all  . Also,
. Also,  for all
for all  .
.
Finally, we prove that  satisfies (b
satisfies (b ).
).  , there exist
, there exist  with
with  (because
(because  is totally ordered) and
is totally ordered) and  such that
such that  . If
. If  (or
(or  ), then
), then  and
and  are ordered by (b
are ordered by (b ). If
). If  , from (b
, from (b ) and (b
) and (b ) it follows that
) it follows that  , which shows that
, which shows that  . To conclude,
. To conclude,  is totally ordered. Noting that both
is totally ordered. Noting that both  and
and  have supremums, by the definition of
have supremums, by the definition of  , we have
, we have

Therefore,

This shows that  satisfies (b
satisfies (b ). Consequently,
). Consequently,  which completes this proof.
which completes this proof.
3. Main Results
Now we can state and prove our main results.
Definition 3.1.
 is said to be a fixed point of the multivalued operator
is said to be a fixed point of the multivalued operator  if
if  . The fixed point
. The fixed point  of
of  is said to be a maximal fixed point of
is said to be a maximal fixed point of  if
if  whenever
whenever  and
and  . If
. If  is a fixed point and if
is a fixed point and if  whenever
whenever  and
and  , we say that
, we say that  is a minimal fixed point of
is a minimal fixed point of  .
.
Theorem 3.2.
Assume that  is an ordered topological space. Let
is an ordered topological space. Let  ,
,  be nonempty and the multivalued operator
be nonempty and the multivalued operator  have sup-closed values such that hypotheses (H1)–(H3) hold. Then
have sup-closed values such that hypotheses (H1)–(H3) hold. Then  admits at least one fixed point in
admits at least one fixed point in  .
.
Proof.
If  has a maximal element
has a maximal element  , then
, then  is a fixed point of
is a fixed point of  . In fact, since
. In fact, since  , we can find
, we can find  such that
such that  . From the definition of
. From the definition of  we can let
we can let  . This implies
. This implies  . We claim that
. We claim that  . Suppose that
. Suppose that  , then
, then  and
and  . Take empty set as a link of linking
. Take empty set as a link of linking  with
with  , we have
, we have  , which contradicts the definition of maximal element.
, which contradicts the definition of maximal element.
To prove the existence of maximal element of  , by Zorn's lemma, is thus sufficient to show that every totally ordered subset of
, by Zorn's lemma, is thus sufficient to show that every totally ordered subset of  has an upper bound. Let
has an upper bound. Let  be any such a subset of
be any such a subset of  . To this purpose, we consider the set
. To this purpose, we consider the set  . Obviously,
. Obviously,  . We claim that
. We claim that  is totally ordered. Indeed, for any
is totally ordered. Indeed, for any  there exist
there exist  and
and  such that
such that  . If
. If  , then
, then  is ordered. Otherwise, we can assume that
is ordered. Otherwise, we can assume that  , thus, from Lemma 2.8 and (b
, thus, from Lemma 2.8 and (b ) it follows that
) it follows that  . Conclusively,
. Conclusively,  is a totally ordered subset.
is a totally ordered subset.
We will prove that any countable totally ordered subset of  has a supremum. It is enough to prove that any given strictly monotone sequence
has a supremum. It is enough to prove that any given strictly monotone sequence  of
of  there is a supremum. From the definition of
there is a supremum. From the definition of  , there exist
, there exist  and
and  such that
such that  for
for  For any
For any  , from the definition of
, from the definition of  , it follows
, it follows  has a supremum. Moreover, Lemma 2.4 guarantees that
has a supremum. Moreover, Lemma 2.4 guarantees that  has a supremum if
has a supremum if  with
with  for some given
for some given  . It is suffices to consider the fact that there exists a subsequence of
. It is suffices to consider the fact that there exists a subsequence of  (without loss of generality, we may assume that it is
(without loss of generality, we may assume that it is  itself) such that
itself) such that  .
.
Case 1.
If  is strictly increasing, then
is strictly increasing, then  . We claim that
. We claim that

If it is contrary, there exists some  such that
such that  . It is easy to know that
. It is easy to know that  . (b
. (b ) implies that
) implies that  , therefore,
, therefore,  . This contradicts
. This contradicts  increasing. The claim follows.
increasing. The claim follows.
Taking  as the link of linking
as the link of linking  with
with  for
for  Let
Let

(b ) shows that
) shows that  is countable totally ordered. For any
is countable totally ordered. For any  , there exists
, there exists  such that
such that  . If
. If  , by means of (b
, by means of (b ) and
) and

we have

If  with
with  , then, by (3.3),
, then, by (3.3),  . If
. If  with
with  , then from condition (b
, then from condition (b ) it follows that
) it follows that  . To sum up,
. To sum up,  , which, combining the condition (H1), yields that
, which, combining the condition (H1), yields that  has a supremum. Hence, by Lemma 2.4,
has a supremum. Hence, by Lemma 2.4,  has a supremum.
has a supremum.
Case 2.
It is clear that  has a supremum when
has a supremum when  is decreasing.
is decreasing.
Now, we prove that  has a maximal element. Suppose, on the contrary, for any
has a maximal element. Suppose, on the contrary, for any  , that there exists
, that there exists  such that
such that  and
and  . Let
. Let  , then
, then  is an operator mapping
is an operator mapping  into
into  and satisfies
and satisfies  and
and  for every
for every  . In virtue of Lemma 2.5, there exists
. In virtue of Lemma 2.5, there exists  such that
such that  . On the other hand, by the definition of
. On the other hand, by the definition of  , we have
, we have  and
and  , a contradiction. Therefore,
, a contradiction. Therefore,  has a maximal element, that is, there exists
has a maximal element, that is, there exists  such that
such that  for all
for all  .
.
Finally, we shall prove that  is an upper bound of
is an upper bound of  . Since
. Since  , there exists
, there exists  and
and  such that
such that  , which implies that
, which implies that  On the other hand, since
On the other hand, since  , we have
, we have  . This compels
. This compels  . Taking empty set as a link of linking
. Taking empty set as a link of linking  with
with  , we have that
, we have that  . Given
. Given  , in virtue of
, in virtue of  being totally ordered, or
being totally ordered, or  which implies
which implies  ; or
; or  , which, applying (b
, which, applying (b ), yields
), yields  . Therefore,
. Therefore,  . Noting that
. Noting that  , we have that
, we have that  . Conclusively,
. Conclusively,  , so, by (a) we have
, so, by (a) we have  . This shows that
. This shows that  is an upper bound of
is an upper bound of  . This proof is completed.
. This proof is completed.
Remark 3.3.
We observe that the result of Theorem 3.2 is true under assumptions of Theorem 3.2 if all  are written as
are written as  The following corollary shows that Theorem 3.2 extends and improves the results of [8].
The following corollary shows that Theorem 3.2 extends and improves the results of [8].
Corollary 3.4.
Let  be an ordered Banach space,
be an ordered Banach space,  be a multivalued operator having nonempty and weakly closed values. Assume that there exists
be a multivalued operator having nonempty and weakly closed values. Assume that there exists  such that conditions (H2), (H3) and (H) hold, then
such that conditions (H2), (H3) and (H) hold, then  has at least a fixed point.
has at least a fixed point.
Proof.
Lemma 2.1 shows that there exists  such that
such that  for all
for all  . By means of Eberlein's theorem and Lemma 2.2 we have that
. By means of Eberlein's theorem and Lemma 2.2 we have that  is the supremum of
is the supremum of  , that is, (H1) is satisfied. Moreover, this implies that
, that is, (H1) is satisfied. Moreover, this implies that  , that is,
, that is,  is upper sequentially order closed in the sense of "weak." Since
is upper sequentially order closed in the sense of "weak." Since  has weakly closed values,
has weakly closed values,  has sup-closed values. From Remark 3.3
has sup-closed values. From Remark 3.3 has a fixed point.
has a fixed point.
Corollary 3.5.
Let  be a weakly sequently completed ordered Banach space,
be a weakly sequently completed ordered Banach space,  a normal cone. If the operator
a normal cone. If the operator  is bounded and satisfies conditions (H2) and (H3), then
is bounded and satisfies conditions (H2) and (H3), then  has at least one fixed point in
has at least one fixed point in  .
.
Proof.
It is suffice to prove that condition (H1) holds. Under these hypotheses, every bounded subset is weakly relatively compact (see [4]), which implies that (H1) is true.
In what follows, we shall consider the existence of maximal and minimal fixed points.
Theorem 3.6.
Under assumptions of Theorem 3.2,  has a minimal fixed point in
has a minimal fixed point in  .
.
Proof.
Let  denote the set consisting of fixed points of
denote the set consisting of fixed points of  . From Theorem 3.2 it follows that
. From Theorem 3.2 it follows that  is nonempty. Set
is nonempty. Set  for
for  . Clearly,
. Clearly,  and
and  is a partially ordered set. By the same methods as to prove Theorem 3.2, we can prove that
is a partially ordered set. By the same methods as to prove Theorem 3.2, we can prove that  has a maximal element
has a maximal element  and
and  is a fixed point of
is a fixed point of  in
in  . It is easy to see that
. It is easy to see that  is minimal fixed point of
is minimal fixed point of  . This completes the proof of Theorem 3.6.
. This completes the proof of Theorem 3.6.
The next result is dual to that of Theorem 3.6.
Theorem 3.7.
Assume that  is an ordered topological space. Let
is an ordered topological space. Let  ,
,  be nonempty and the multivalued operator
be nonempty and the multivalued operator  have inf-closed values such that the following hypotheses are satisfied.
have inf-closed values such that the following hypotheses are satisfied.
(h1)If  is a countable totally ordered set and
is a countable totally ordered set and  , then
, then  has a infimum.
has a infimum.
(h2) is increasing downwards and
is increasing downwards and  .
.
(h3) , where
, where  stands for a set which consists of all infimums of
stands for a set which consists of all infimums of  (its definition is similar to
(its definition is similar to  ).
).
Then  admits at least one fixed point in
admits at least one fixed point in  .
.
Theorem 3.8.
Assume that the operator  is increasing and satisfies conditions (H1)–(H3) and (h1)–(h3), then
is increasing and satisfies conditions (H1)–(H3) and (h1)–(h3), then  has maximal and minimal fixed points on
has maximal and minimal fixed points on  .
.
Remark 3.9.
If  has the limit ordinal property,
has the limit ordinal property,  is increasing and has nonempty closed values. Assume that
is increasing and has nonempty closed values. Assume that  is relatively sequentially compact and conditions (H3) and (h3) hold, then
is relatively sequentially compact and conditions (H3) and (h3) hold, then  has sup-closed and inf-closed values and satisfies conditions (H1) and (h1) on
has sup-closed and inf-closed values and satisfies conditions (H1) and (h1) on  . Thereby,
. Thereby,  has maximal and minimal fixed points on
has maximal and minimal fixed points on  . In this sense, we extend and improve the corresponding results of Theorem 2.1 in [10].
. In this sense, we extend and improve the corresponding results of Theorem 2.1 in [10].
Corollary 3.10.
Let  be a partially ordered Banach space. If there exist
be a partially ordered Banach space. If there exist  with
with  such that
such that  . Assume that
. Assume that  is increasing, has nonempty closed values, and satisfies one of the following hypotheses, then
is increasing, has nonempty closed values, and satisfies one of the following hypotheses, then  has maximal and minimal fixed points on
has maximal and minimal fixed points on  .
.
(s1) is a regular cone.
is a regular cone.
(s2) If  is countable totally ordered subset and
is countable totally ordered subset and  then
then  is relatively compact subset.
is relatively compact subset.
(s3) is a weakly relatively compact set.
is a weakly relatively compact set.
(s4) is a bounded ordered interval, and for any countable noncompact subset
is a bounded ordered interval, and for any countable noncompact subset  with
with  , one has
, one has  , where
, where  denotes Kuratowskii's noncompactness measure.
denotes Kuratowskii's noncompactness measure.
Proof.
(s2) implies (H1) and (h1) holds. The rest is clear.
Remark 3.11.
(s2) is main condition of [12] for single-valued operators, (s4) is main condition of [13]. Hence the results presented here extend and improve the corresponding results of the above mentioned papers.
4. Application
In this section we assume that  is a Banach space with partial ordering derived by the continuous bounded function
is a Banach space with partial ordering derived by the continuous bounded function  as follows (see [14]):
as follows (see [14]):

To illustrate the ideas involved in Theorem 3.8 we discuss the Hammerstein integral inclusions of the form

Here  is a real single-valued function, while
is a real single-valued function, while  is a multivalued map with nonempty closed values.
is a multivalued map with nonempty closed values.
Let  and
and  be the conjugate exponent of
be the conjugate exponent of  , that is,
, that is,  . Let
. Let  denote the norm of the space
denote the norm of the space  . For
. For  stipulate that
stipulate that  if and only if
if and only if  with all
with all  .
.
In order to prove the existence of solutions to (4.2) in  we assume the following.
we assume the following.
(S1)The function  satisfies that
satisfies that  and
and  belongs to
belongs to  .
.
(S2) is increasing with regard to
is increasing with regard to  for fixed
for fixed  .
.
(S3)There exist  with
with  such that
such that  and
and  for every
for every  .
.
(S4) has a strongly measurable selection on
has a strongly measurable selection on  for each
for each  .
.
(S5) a.e. on
a.e. on  for all
for all  . Here
. Here  .
.
Theorem 4.1.
Assume that conditions (S1)–(S5) hold, then (4.2) has maximal and minimal solutions in  .
.
Proof.
Define a multivalued operator  as follows:
as follows:

(S4) guarantees that  makes sense. For any
makes sense. For any  with
with  , there exists
, there exists  such that
such that  . From (
. From ( ) and Hölder inequality, it follows that
) and Hölder inequality, it follows that

This implies that  , that is,
, that is,  maps
maps  into itself. We seek to apply Theorem 3.8. Note that (S1) and (S3) guarantee that
into itself. We seek to apply Theorem 3.8. Note that (S1) and (S3) guarantee that  . For every given
. For every given  and any
and any  , set
, set  with
with  for
for  Thus,
Thus,  is a decreasing sequence. Note that
is a decreasing sequence. Note that  is a bounded function, we obtain that the sequence
is a bounded function, we obtain that the sequence  is convergent. Hence, for any
is convergent. Hence, for any  , there exists a natural number
, there exists a natural number  such that
such that

whenever  . This shows that
. This shows that  is a Cauchy sequence, thereby
is a Cauchy sequence, thereby  is convergent. Lemma 2.2 guarantees
is convergent. Lemma 2.2 guarantees  , which yields
, which yields  . From the arbitrariness of
. From the arbitrariness of  it follows that
it follows that  is supremum of
is supremum of  . From (4.4) and the dominated convergence theorem, it follows that
. From (4.4) and the dominated convergence theorem, it follows that  . Moreover,
. Moreover,  for
for  . Consequently,
. Consequently,  . Similarly, we have
. Similarly, we have  . This shows that (H3) and (h3) are satisfied for
. This shows that (H3) and (h3) are satisfied for  . (S2) guarantees that
. (S2) guarantees that  is increasing. It is easy to see that
is increasing. It is easy to see that  has closed values. This yields that
has closed values. This yields that  has sup-closed and inf-closed values.
has sup-closed and inf-closed values.
Finally, we check conditions (H1) and (h1). Suppose that the set  is countable, totally ordered, and satisfies
is countable, totally ordered, and satisfies  for all
for all  . We have to prove that the set
. We have to prove that the set  has a supremum. Since
has a supremum. Since  is countable totally ordered, we can assume
is countable totally ordered, we can assume  with
with  for
for  This implies that the sequence
This implies that the sequence  is decreasing. In the same way, we can prove that the sequence
is decreasing. In the same way, we can prove that the sequence  is convergent. Again, Lemma 2.2 guarantees that
is convergent. Again, Lemma 2.2 guarantees that  has a supremum, which implies that condition (H1) is satisfied. Similarly, we can prove that condition (h1) holds. All conditions of Theorem 3.8 are satisfied, consequently, the operator
has a supremum, which implies that condition (H1) is satisfied. Similarly, we can prove that condition (h1) holds. All conditions of Theorem 3.8 are satisfied, consequently, the operator  has minimum and maximum fixed points in
has minimum and maximum fixed points in  and this proof is completed.
and this proof is completed.
Remark 4.2.
By comparing the results of Theorem 4.2 in [15] in which Couchouron and Precup have proved that (4.2) has at least one solution, we omit the conditions that  is continuous and has compact values in Theorem 4.1.
is continuous and has compact values in Theorem 4.1.
References
Banach S: Surles opérations dans les ensembles abstraits et leur application aux équations integrales. Fundamenta Mathematicae 1922, 3: 133–181.
Kirk WA: A fixed point theorem for mappings which do not increase distances. The American Mathematical Monthly 1965, 72: 1004–1006. 10.2307/2313345
Mönch H: Boundary value problems for nonlinear ordinary differential equations of second order in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 1980,4(5):985–999. 10.1016/0362-546X(80)90010-3
Cromme LJ, Diener I: Fixed point theorems for discontinuous mapping. Mathematical Programming 1991,51(1–3):257–267.
Kirk WA: Hölder continuity and minimal displacement. Numerical Functional Analysis and Optimization 1998,19(1–2):71–79. 10.1080/01630569808816815
Kirk WA, Saliga LM: Some results on existence and approximation in metric fixed point theory. Journal of Computational and Applied Mathematics 2000,113(1):141–152. 10.1016/S0377-0427(99)00249-6
Dhage BC: Fixed-point theorems for discontinuous multivalued operators on ordered spaces with applications. Computers and Mathematics with Applications 2006,51(3–4):589–604. 10.1016/j.camwa.2005.07.017
Hong SH: Fixed points of discontinuous multivalued increasing operators in Banach spaces with applications. Journal of Mathematical Analysis and Applications 2003,282(1):151–162. 10.1016/S0022-247X(03)00111-2
Hong SH: Fixed points for mixed monotone multivalued operators in Banach spaces with applications. Journal of Mathematical Analysis and Applications 2008,337(1):333–342. 10.1016/j.jmaa.2007.03.091
Carl S, Heikkilä S: Fixed point theorems for multifunctions with applications to discontinuous operator and differential equations. Journal of Mathematical Analysis and Applications 2004,297(1):56–69. 10.1016/j.jmaa.2004.03.061
Huy NB: Fixed points of increasing multivalued operators and an application to discontinuous elliptic equations. Nonlinear Analysis: Theory, Methods & Applications 2002,51(4):673–678. 10.1016/S0362-546X(01)00850-1
Guo D, Sun J, Liu Z: Functional Method of Nonlinear Ordinary Differential Equations. Shandong Science and Technology Press, Jinan, China; 1995.
Chang S, Ma Y: Coupled fixed points for mixed monotone condensing operators and an existence theorem of the solutions for a class of functional equations arising in dynamic programming. Journal of Mathematical Analysis and Applications 1991,160(2):468–479. 10.1016/0022-247X(91)90319-U
Caristi J: Fixed point theorems for mappings satisfying inwardness conditions. Transactions of the American Mathematical Society 1976, 215: 241–251.
Couchouron J-F, Precup R: Existence principles for inclusions of Hammerstein type involving noncompact acyclic multivalued maps. Electronic Journal of Differential Equations 2002,2002(4):-21.
Acknowledgments
This work was supported by the Natural Science Foundation of Zhejiang Province (Y607178) and the Natural Science Foundation of China (10771048).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hong, S., Qiu, Z. Fixed Points of Discontinuous Multivalued Operators in Ordered Spaces with Applications. Fixed Point Theory Appl 2010, 745769 (2010). https://doi.org/10.1155/2010/745769
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/745769
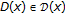 we take
we take 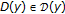 such that
such that 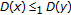 and we can find
and we can find  such that
such that 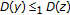 . It is sufficient to assume that at least one of the above equalities does not hold. The definition of
. It is sufficient to assume that at least one of the above equalities does not hold. The definition of  guarantees that
guarantees that