- Research Article
- Open access
- Published:
Weak and Strong Convergence of an Implicit Iteration Process for an Asymptotically Quasi-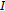 -Nonexpansive Mapping in Banach Space
-Nonexpansive Mapping in Banach Space
Fixed Point Theory and Applications volume 2010, Article number: 719631 (2009)
Abstract
We prove the weak and strong convergence of the implicit iterative process to a common fixed point of an asymptotically quasi- -nonexpansive mapping
-nonexpansive mapping  and an asymptotically quasi-nonexpansive mapping
and an asymptotically quasi-nonexpansive mapping  , defined on a nonempty closed convex subset of a Banach space.
, defined on a nonempty closed convex subset of a Banach space.
1. Introduction
Let  be a nonempty subset of a real normed linear space
be a nonempty subset of a real normed linear space  and let
and let  be a mapping. Denote by
be a mapping. Denote by  the set of fixed points of
the set of fixed points of  , that is,
, that is,  . Throughout this paper, we always assume that
. Throughout this paper, we always assume that  . Now let us recall some known definitions.
. Now let us recall some known definitions.
Definition 1.1.
A mapping  is said to be
is said to be
(i)nonexpansive, if  for all
for all  ;
;
(ii)asymptotically nonexpansive, if there exists a sequence  with
with  such that
such that  for all
for all  and
and  ;
;
(iii)quasi-nonexpansive, if  for all
for all  ;
;
(iv)asymptotically quasi-nonexpansive, if there exists a sequence  with
with  such that
such that  for all
for all  and
and  .
.
Note that from the above definitions, it follows that a nonexpansive mapping must be asymptotically nonexpansive, and an asymptotically nonexpansive mapping must be asymptotically quasi-nonexpansive, but the converse does not hold (see [1]).
If  is a closed nonempty subset of a Banach space and
is a closed nonempty subset of a Banach space and  is nonexpansive, then it is known that
is nonexpansive, then it is known that  may not have a fixed point (unlike the case if
may not have a fixed point (unlike the case if  is a strict contraction), and even when it has, the sequence
is a strict contraction), and even when it has, the sequence  defined by
defined by  (the so-called Picard sequence) may fail to converge to such a fixed point.
(the so-called Picard sequence) may fail to converge to such a fixed point.
In [2, 3] Browder studied the iterative construction for fixed points of nonexpansive mappings on closed and convex subsets of a Hilbert space. Note that for the past 30 years or so, the studies of the iterative processes for the approximation of fixed points of nonexpansive mappings and fixed points of some of their generalizations have been flourishing areas of research for many mathematicians (see for more details [1, 4]).
In [5] Diaz and Metcalf studied quasi-nonexpansive mappings in Banach spaces. Ghosh and Debnath [6] established a necessary and sufficient condition for convergence of the Ishikawa iterates of a quasi-nonexpansive mapping on a closed convex subset of a Banach space. The iterative approximation problems for nonexpansive mapping, asymptotically nonexpansive mapping and asymptotically quasi-nonexpansive mapping were studied extensively by Goebel and Kirk [7], Liu [8], Wittmann [9], Reich [10], Gornicki [11], Schu [12] Shioji and Takahashi [13], and Tan and Xu [14] in the settings of Hilbert spaces and uniformly convex Banach spaces.
There are many methods for approximating fixed points of a nonexpansive mapping. Xu and Ori [15] introduced implicit iteration process to approximate a common fixed point of a finite family of nonexpansive mappings in a Hilbert space. Recently, Sun [16] has extended an implicit iteration process for a finite family of nonexpansive mappings, due to Xu and Ori, to the case of asymptotically quasi-nonexpansive mappings in a setting of Banach spaces. In [17] it has been studied the weak and strong convergence of implicit iteration process with errors to a common fixed point for a finite family of nonexpansive mappings in Banach spaces, which extends and improves the mentioned papers (see also [18, 19] for applications and other methods of implicit iteration processes).
There are many concepts which generalize a notion of nonexpansive mapping. One of such concepts is  -nonexpansivity of a mapping
-nonexpansivity of a mapping  ([20]). Let us recall some notions.
([20]). Let us recall some notions.
Definition 1.2.
Let  ,
,  be two mappings of a nonempty subset
be two mappings of a nonempty subset  of a real normed linear space
of a real normed linear space  . Then
. Then  is said to be
is said to be
(i) - nonexpansive, if
- nonexpansive, if  for all
for all  ;
;
(ii)asymptotically  - nonexpansive, if there exists a sequence
- nonexpansive, if there exists a sequence  with
with  such that
such that  for all
for all  and
and  ;
;
(iii)asymptotically quasi  - nonexpansive mapping, if there exists a sequence
- nonexpansive mapping, if there exists a sequence  with
with  such that
such that  for all
for all  and
and 
Remark 1.3.
If  then an asymptotically
then an asymptotically  -nonexpansive mapping is asymptotically quasi-
-nonexpansive mapping is asymptotically quasi- -nonexpansive. But, there exists a nonlinear continuous asymptotically quasi
-nonexpansive. But, there exists a nonlinear continuous asymptotically quasi  -nonexpansive mappings which is asymptotically
-nonexpansive mappings which is asymptotically  -nonexpansive.
-nonexpansive.
In [21] a weakly convergence theorem for  -asymptotically quasi-nonexpansive mapping defined in Hilbert space was proved. In [22] strong convergence of Mann iterations of
-asymptotically quasi-nonexpansive mapping defined in Hilbert space was proved. In [22] strong convergence of Mann iterations of  -nonexpansive mapping has been proved. Best approximation properties of
-nonexpansive mapping has been proved. Best approximation properties of  -nonexpansive mappings were investigated in [20]. In [23] the weak convergence of three-step Noor iterative scheme for an
-nonexpansive mappings were investigated in [20]. In [23] the weak convergence of three-step Noor iterative scheme for an  -nonexpansive mapping in a Banach space has been established. Recently, in [24] the weak and strong convergence of implicit iteration process to a common fixed point of a finite family of
-nonexpansive mapping in a Banach space has been established. Recently, in [24] the weak and strong convergence of implicit iteration process to a common fixed point of a finite family of  -asymptotically nonexpansive mappings were studied. Assume that the family consists of one
-asymptotically nonexpansive mappings were studied. Assume that the family consists of one  -asymptotically nonexpansive mapping
-asymptotically nonexpansive mapping  . Now let us consider an iteration method used in [24], for
. Now let us consider an iteration method used in [24], for  , which is defined by
, which is defined by

where  and
and  are two sequences in
are two sequences in  . From this formula one can easily see that the employed method, indeed, is not implicit iterative processes. The used process is some kind of modified Ishikawa iteration.
. From this formula one can easily see that the employed method, indeed, is not implicit iterative processes. The used process is some kind of modified Ishikawa iteration.
Therefore, in this paper we will extend of the implicit iterative process, defined in [16], to  -asymptotically quasi-nonexpansive mapping defined on a uniformly convex Banach space. Namely, let
-asymptotically quasi-nonexpansive mapping defined on a uniformly convex Banach space. Namely, let  be a nonempty convex subset of a real Banach space
be a nonempty convex subset of a real Banach space  and
and  be an asymptotically quasi
be an asymptotically quasi  -nonexpansive mapping, and let
-nonexpansive mapping, and let  be an asymptotically quasi-nonexpansive mapping. Then for given two sequences
be an asymptotically quasi-nonexpansive mapping. Then for given two sequences  and
and  in
in  we will consider the following iteration scheme:
we will consider the following iteration scheme:

In this paper we will prove the weak and strong convergences of the implicit iterative process (1.2) to a common fixed point of  and
and  . All results presented here generalize and extend the corresponding main results of [15–17] in a case of one mapping.
. All results presented here generalize and extend the corresponding main results of [15–17] in a case of one mapping.
2. Preliminaries
Throughout this paper, we always assume that  is a real Banach space. We denote by
is a real Banach space. We denote by  and
and  the set of fixed points and the domain of a mapping
the set of fixed points and the domain of a mapping  respectively. Recall that a Banach space
respectively. Recall that a Banach space  is said to satisfy Opial condition [25], if for each sequence
is said to satisfy Opial condition [25], if for each sequence  in
in 
 converging weakly to
converging weakly to  implies that
implies that

for all  with
with  It is well known that (see [26]) inequality (2.1) is equivalent to
It is well known that (see [26]) inequality (2.1) is equivalent to

Definition 2.1.
Let  be a closed subset of a real Banach space
be a closed subset of a real Banach space  and let
and let  be a mapping.
be a mapping.
(i)A mapping  is said to be semiclosed (demiclosed) at zero, if for each bounded sequence
is said to be semiclosed (demiclosed) at zero, if for each bounded sequence  in
in  the conditions
the conditions  converges weakly to
converges weakly to  and
and  converges strongly to
converges strongly to  imply
imply 
(ii)A mapping  is said to be semicompact, if for any bounded sequence
is said to be semicompact, if for any bounded sequence  in
in  such that
such that  then there exists a subsequence
then there exists a subsequence  such that
such that  strongly.
strongly.
(iii) is called a uniformly
is called a uniformly  -Lipschitzian mapping, if there exists a constant
-Lipschitzian mapping, if there exists a constant  such that
such that  for all
for all  and
and 
The following lemmas play an important role in proving our main results.
Lemma 2.2 (see [12]).
Let  be a uniformly convex Banach space and let
be a uniformly convex Banach space and let  be two constants with
be two constants with  Suppose that
Suppose that  is a sequence in
is a sequence in  and
and  and
and  are two sequences in
are two sequences in  such that
such that

holds some  Then
Then 
Lemma 2.3 (see [14]).
Let  and
and  be two sequences of nonnegative real numbers with
be two sequences of nonnegative real numbers with  If one of the following conditions is satisfied:
If one of the following conditions is satisfied:
(i)
(ii)
then the limit  exists.
exists.
3. Main Results
In this section we will prove our main results. To formulate one, we need some auxiliary results.
Lemma 3.1.
Let  be a real Banach space and let
be a real Banach space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  Let
Let  be an asymptotically quasi
be an asymptotically quasi  -nonexpansive mapping with a sequence
-nonexpansive mapping with a sequence  and
and  be an asymptotically quasi-nonexpansive mapping with a sequence
be an asymptotically quasi-nonexpansive mapping with a sequence  such that
such that  Suppose
Suppose 

 and
and  and
and  are two sequences in
are two sequences in  which satisfy the following conditions:
which satisfy the following conditions:
(i)
(ii)
If  is the implicit iterative sequence defined by (1.2), then for each
is the implicit iterative sequence defined by (1.2), then for each  the limit
the limit  exists.
exists.
Proof.
Since  for any given
for any given  it follows from (1.2) that
it follows from (1.2) that

Again from (1.2) we derive that

which means

Then from (3.3) one finds

and so

By condition (ii) we have  and therefore
and therefore

Hence from (3.5) we obtain

By putting  the last inequality can be rewritten as follows:
the last inequality can be rewritten as follows:

From condition (i) we find

Denoting  in (3.8) one gets
in (3.8) one gets

and Lemma 2.3 implies the existence of the limit  . This means the limit
. This means the limit

exists, where  is a constant. This completes the proof.
is a constant. This completes the proof.
Now we prove the following result.
Theorem 3.2.
Let  be a real Banach space and let
be a real Banach space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  Let
Let  be a uniformly
be a uniformly  -Lipschitzian asymptotically quasi-
-Lipschitzian asymptotically quasi- -nonexpansive mapping with a sequence
-nonexpansive mapping with a sequence  and let
and let  be a uniformly
be a uniformly  -Lipschitzian asymptotically quasi-nonexpansive mapping with a sequence
-Lipschitzian asymptotically quasi-nonexpansive mapping with a sequence  such that
such that  Suppose
Suppose 

 and
and  and
and  are two sequences in
are two sequences in  which satisfy the following conditions:
which satisfy the following conditions:
(i)
(ii)
Then the implicitly iterative sequence  defined by (1.2) converges strongly to a common fixed point in
defined by (1.2) converges strongly to a common fixed point in  if and only if
if and only if

Proof.
The necessity of condition (3.12) is obvious. Let us proof the sufficiency part of theorem.
Since  are uniformly
are uniformly  -Lipschitzian mappings, so
-Lipschitzian mappings, so  and
and  are continuous mappings. Therefore the sets
are continuous mappings. Therefore the sets  and
and  are closed. Hence
are closed. Hence  is a nonempty closed set.
is a nonempty closed set.
For any given  we have (see (3.8))
we have (see (3.8))

here as before  with
with  Hence, one finds
Hence, one finds

From (3.14) due to Lemma 2.3 we obtain the existence of the limit  . By condition (3.12), one gets
. By condition (3.12), one gets

Let us prove that the sequence  converges to a common fixed point of
converges to a common fixed point of  and
and  In fact, due to
In fact, due to  for all
for all  and from (3.13), we obtain
and from (3.13), we obtain

Hence, for any positive integers  from (3.16) with
from (3.16) with  we find
we find

which means that

for all  , where
, where 
Since  then for any given
then for any given  there exists a positive integer number
there exists a positive integer number  such that
such that

Therefore there exists  such that
such that

Consequently, for all  from (3.18) we derive
from (3.18) we derive

which means that the strong convergence of the sequence  is a common fixed point
is a common fixed point  of
of  and
and  This proves the required assertion.
This proves the required assertion.
We need one more auxiliary result.
Proposition 3.3.
Let  be a real uniformly convex Banach space and let
be a real uniformly convex Banach space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  Let
Let  be a uniformly
be a uniformly  -Lipschitzian asymptotically quasi-
-Lipschitzian asymptotically quasi- -nonexpansive mapping with a sequence
-nonexpansive mapping with a sequence  and let
and let  be a uniformly
be a uniformly  -Lipschitzian asymptotically quasi-nonexpansive mapping with a sequence
-Lipschitzian asymptotically quasi-nonexpansive mapping with a sequence  such that
such that  Suppose
Suppose 


 and
and  and
and  are two sequences in
are two sequences in  which satisfy the following conditions:
which satisfy the following conditions:
(i)
(ii)
(iii)
Then the implicitly iterative sequence  defined by (1.2) satisfies the following:
defined by (1.2) satisfies the following:

Proof.
First, we will prove that

According to Lemma 3.1 for any  we have
we have  . It follows from (1.2) that
. It follows from (1.2) that

By means of asymptotically quasi- -nonexpansivity of
-nonexpansivity of  and asymptotically quasi-nonexpansivity of
and asymptotically quasi-nonexpansivity of  from (3.3) we get
from (3.3) we get

Now using

with (3.25) and applying Lemma 2.2 to (3.24) one finds

Now from (1.2) and (3.27) we infer that

On the other hand, we have

which implies

The last inequality with (3.3) yields that

Then (3.27) and (3.24) with the Squeeze theorem imply that

Again from (1.2) we can see that

From (3.11) one finds

Now applying Lemma 2.2 to (3.33) we obtain

Consider

Then from (3.27), (3.28), and (3.35) we get

Finally, from

with (3.28) and (3.37) we obtain

Analogously, one has

which with (3.28) and (3.35) implies

Now we are ready to formulate one of main results concerning weak convergence of the sequence  .
.
Theorem 3.4.
Let  be a real uniformly convex Banach space satisfying Opial condition and let
be a real uniformly convex Banach space satisfying Opial condition and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  Let
Let  be an identity mapping, let
be an identity mapping, let  be a uniformly
be a uniformly  -Lipschitzian asymptotically quasi-
-Lipschitzian asymptotically quasi- -nonexpansive mapping with a sequence
-nonexpansive mapping with a sequence  and,
and,  be a uniformly
be a uniformly  -Lipschitzian asymptotically quasi-nonexpansive mapping with a sequence
-Lipschitzian asymptotically quasi-nonexpansive mapping with a sequence  such that
such that  Suppose
Suppose 

 and
and  and
and  are two sequences in
are two sequences in  satisfying the following conditions:
satisfying the following conditions:
(i)
(ii)
(iii)
If the mappings  and
and  are semiclosed at zero, then the implicitly iterative sequence
are semiclosed at zero, then the implicitly iterative sequence  defined by (1.2) converges weakly to a common fixed point of
defined by (1.2) converges weakly to a common fixed point of  and
and 
Proof.
Let  , then according to Lemma 3.1 the sequence
, then according to Lemma 3.1 the sequence  converges. This provides that
converges. This provides that  is a bounded sequence. Since
is a bounded sequence. Since  is uniformly convex, then every bounded subset of
is uniformly convex, then every bounded subset of  is weakly compact. Since
is weakly compact. Since  is a bounded sequence in
is a bounded sequence in  then there exists a subsequence
then there exists a subsequence  such that
such that  converges weakly to
converges weakly to  Hence from (3.39) and (3.41) it follows that
Hence from (3.39) and (3.41) it follows that

Since the mappings  and
and  are semiclosed at zero, therefore, we find
are semiclosed at zero, therefore, we find  and
and  which means
which means 
Finally, let us prove that  converges weakly to
converges weakly to  In fact, suppose the contrary, that is, there exists some subsequence
In fact, suppose the contrary, that is, there exists some subsequence  such that
such that  converges weakly to
converges weakly to  and
and  . Then by the same method as given above, we can also prove that
. Then by the same method as given above, we can also prove that 
Taking  and
and  and using the same argument given in the proof of (3.11), we can prove that the limits
and using the same argument given in the proof of (3.11), we can prove that the limits  and
and  exist, and we have
exist, and we have

where  are two nonnegative numbers. By virtue of the Opial condition of
are two nonnegative numbers. By virtue of the Opial condition of  , one finds
, one finds

This is a contradiction. Hence  This implies that
This implies that  converges weakly to
converges weakly to  This completes the proof of Theorem 3.4.
This completes the proof of Theorem 3.4.
Now we formulate next result concerning strong convergence of the sequence  .
.
Theorem 3.5.
Let  be a real uniformly convex Banach space and let
be a real uniformly convex Banach space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  Let
Let  be a uniformly
be a uniformly  -Lipschitzian asymptotically quasi-
-Lipschitzian asymptotically quasi- -nonexpansive mapping with a sequence
-nonexpansive mapping with a sequence  and
and  be a uniformly
be a uniformly  -Lipschitzian asymptotically quasi-nonexpansive mapping with a sequence
-Lipschitzian asymptotically quasi-nonexpansive mapping with a sequence  such that
such that  Suppose
Suppose 


 and
and  and
and  are two sequences in
are two sequences in  satisfying the following conditions:
satisfying the following conditions:
(i)
(ii)
(iii)
If at least one mapping of the mappings  and
and  is semicompact, then the implicitly iterative sequence
is semicompact, then the implicitly iterative sequence  defined by (1.2) converges strongly to a common fixed point of
defined by (1.2) converges strongly to a common fixed point of  and
and 
Proof.
Without any loss of generality, we may assume that  is semicompact. This with (3.39) means that there exists a subsequence
is semicompact. This with (3.39) means that there exists a subsequence  such that
such that  strongly and
strongly and  Since
Since  are continuous, then from (3.39) and (3.41) we find
are continuous, then from (3.39) and (3.41) we find

This shows that  According to Lemma 3.1 the limit
According to Lemma 3.1 the limit  exists. Then
exists. Then

which means that  converges to
converges to  This completes the proof.
This completes the proof.
Note that all results presented here generalize and extend the corresponding main results of [15–17] in a case of one mapping.
References
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Browder FE: Nonexpansive nonlinear operators in a Banach space. Proceedings of the National Academy of Sciences of the United States of America 1965, 54: 1041–1044. 10.1073/pnas.54.4.1041
Browder FE: Convergence of approximants to fixed points of nonexpansive non-linear mappings in Banach spaces. Archive for Rational Mechanics and Analysis 1967, 24: 82–90.
Chidume Ch: Geometric Properties of Banach Spaces and Nonlinear Iterations, Lecture Notes in Mathematics. Volume 1965. Springer, London, UK; 2009:xviii+326.
Diaz JB, Metcalf FT: On the structure of the set of subsequential limit points of successive approximations. Bulletin of the American Mathematical Society 1967, 73: 516–519. 10.1090/S0002-9904-1967-11725-7
Ghosh MK, Debnath L: Convergence of Ishikawa iterates of quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 1997,207(1):96–103. 10.1006/jmaa.1997.5268
Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 1972, 35: 171–174. 10.1090/S0002-9939-1972-0298500-3
Liu Q: Iterative sequences for asymptotically quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 2001,259(1):1–7. 10.1006/jmaa.2000.6980
Wittmann R: Approximation of fixed points of nonexpansive mappings. Archiv der Mathematik 1992,58(5):486–491. 10.1007/BF01190119
Reich S: Strong convergence theorems for resolvents of accretive operators in Banach spaces. Journal of Mathematical Analysis and Applications 1980,75(1):287–292. 10.1016/0022-247X(80)90323-6
Gornicki J: Weak convergence theorems for asymptotically nonexpansive mappings in uniformly convex Banach spaces. Commentationes Mathematicae Universitatis Carolinae 1989,30(2):249–252.
Schu J: Weak and strong convergence to fixed points of asymptotically nonexpansive mappings. Bulletin of the Australian Mathematical Society 1991,43(1):153–159. 10.1017/S0004972700028884
Shioji N, Takahashi W: Strong convergence theorems for asymptotically nonexpansive semigroups in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 1998,34(1):87–99. 10.1016/S0362-546X(97)00682-2
Tan K-K, Xu H-K: Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process. Journal of Mathematical Analysis and Applications 1993,178(2):301–308. 10.1006/jmaa.1993.1309
Xu H-K, Ori RG: An implicit iteration process for nonexpansive mappings. Numerical Functional Analysis and Optimization 2001,22(5–6):767–773. 10.1081/NFA-100105317
Sun Z-H: Strong convergence of an implicit iteration process for a finite family of asymptotically quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 2003,286(1):351–358. 10.1016/S0022-247X(03)00537-7
Gu F, Lu J: A new composite implicit iterative process for a finite family of nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2006, 2006:-11.
Li HY, Li HZ: Strong convergence of an iterative method for equilibrium problems and variational inequality problems. Fixed Point Theory and Applications 2009, 2009:-21.
Zhang F, Su Y: Strong convergence of modified implicit iteration processes for common fixed points of nonexpansive mappings. Fixed Point Theory and Applications 2007, 2007:-9.
Shahzad N: Generalized -nonexpansive maps and best approximations in Banach spaces. Demonstratio Mathematica 2004,37(3):597–600.
Temir S, Gul O: Convergence theorem for -asymptotically quasi-nonexpansive mapping in Hilbert space. Journal of Mathematical Analysis and Applications 2007,329(2):759–765. 10.1016/j.jmaa.2006.07.004
Rhodes BH, Temir S: Convergebce thorems for -nonexpansive mapping. International Journal of Mathematics and Mathematical Sciences 2006, 2006:-4.
Kumam P, Kumethong W, Jewwaiworn N: Weak convergence theorems of three-step Noor iterative scheme for -quasi-nonexpansive mappings in Banach spaces. Applied Mathematical Sciences 2008,2(57–60):2915–2920.
Temir S: On the convergence theorems of implicit iteration process for a finite family of -asymptotically nonexpansive mappings. Journal of Computational and Applied Mathematics 2009,225(2):398–405. 10.1016/j.cam.2008.07.049
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bulletin of the American Mathematical Society 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Lami Dozo E: Multivalued nonexpansive mappings and Opial's condition. Proceedings of the American Mathematical Society 1973, 38: 286–292.
Acknowledgment
The authors acknowledge the MOSTI Grant 01-01-08-SF0079.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Mukhamedov, F., Saburov, M. Weak and Strong Convergence of an Implicit Iteration Process for an Asymptotically Quasi-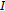 -Nonexpansive Mapping in Banach Space.
Fixed Point Theory Appl 2010, 719631 (2009). https://doi.org/10.1155/2010/719631
-Nonexpansive Mapping in Banach Space.
Fixed Point Theory Appl 2010, 719631 (2009). https://doi.org/10.1155/2010/719631
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/719631