- Research Article
- Open access
- Published:
Some Convergence Theorems of a Sequence in Complete Metric Spaces and Its Applications
Fixed Point Theory and Applications volume 2010, Article number: 647085 (2009)
Abstract
The concept of weakly quasi-nonexpansive mappings with respect to a sequence is introduced. This concept generalizes the concept of quasi-nonexpansive mappings with respect to a sequence due to Ahmed and Zeyada (2002). Mainly, some convergence theorems are established and their applications to certain iterations are given.
1. Introduction
In 1916, Tricomi [1] introduced originally the concept of quasi-nonexpansive for real functions. Subsequently, this concept has studied for mappings in Banach and metric spaces (see, e.g., [2–7]). Recently, some generalized types of quasi-nonexpansive mappings in metric and Banach spaces have appeared. For example, see Ahmed and Zeyada [8], Qihou [9–11] and others.
Unless stated to the contrary, we assume that  is a metric space. Let
is a metric space. Let  be any mapping and let
be any mapping and let  be the set of all fixed points of
be the set of all fixed points of  . If
. If  where
where  is the set of all real numbers and if
is the set of all real numbers and if  , set
, set  . We use the symbol
. We use the symbol  to denote the usual Kuratowski measure of noncompactness. For some properties of
to denote the usual Kuratowski measure of noncompactness. For some properties of  see Zeidler [12, pages 493–495]. For a given
see Zeidler [12, pages 493–495]. For a given  , the Picard iteration
, the Picard iteration  is determined by:
is determined by:
(I)
where  is the set of all positive integers.
is the set of all positive integers.
If  is a normed space,
is a normed space,  is a convex set, and
is a convex set, and  , Ishikawa [13] gave the following iteration:
, Ishikawa [13] gave the following iteration:
(II)
for each  , where
, where  and
and  . When
. When  , it yields that
, it yields that  . Therefore, the iteration scheme (II) becomes
. Therefore, the iteration scheme (II) becomes

This iteration is called Mann iteration [14].
The concepts of quasi-nonexpansive mappings, with respect to a sequence and asymptotically regular mappings at a point were given in metric spaces as follows.
Definition 1.1 (see [6]).
 is said to be quasi-nonexpansive mapping if for each
is said to be quasi-nonexpansive mapping if for each  and for every
and for every  ,
,  .
.
Definition 1.2 (see [8]).
The map  is said to be quasi-nonexpansive with respect to
is said to be quasi-nonexpansive with respect to  if for all
if for all  and for every
and for every  ,
,  .
.
Lemma 2.1 in [8] stated that quasi-nonexpansiveness converts to quasi-nonexpansiveness with respect to  (resp.,
(resp.,  ,
,  ) for each
) for each  . The reverse implication is not true (see, [8, Example 2.1]). Also, the authors [8] showed that the continuity of
. The reverse implication is not true (see, [8, Example 2.1]). Also, the authors [8] showed that the continuity of  leads to the closedness of
leads to the closedness of  and the converse is not true (see, [8, Example 2.2]).
and the converse is not true (see, [8, Example 2.2]).
Definition 1.3 (see [15]).
The mapping  is called an asymptotically regular at a point
is called an asymptotically regular at a point  if
if  .
.
The following definition is given by Angrisani and Clavelli.
Definition 1.4 (see [16]).
Let  be a topological space. The function
be a topological space. The function  is said to be a regular-global-inf (r.g.i) at
is said to be a regular-global-inf (r.g.i) at  if
if  implies that there exists
implies that there exists  such that
such that  and a neighborhood
and a neighborhood  of
of  such that
such that  for each
for each  . If this condition holds for each
. If this condition holds for each  , then
, then  is said to be an r.g.i on
is said to be an r.g.i on  .
.
Definition 1.5 (see [17]).
Let  be a convex subset of a normed space
be a convex subset of a normed space  . A mapping
. A mapping  is called directionally nonexpansive if
is called directionally nonexpansive if  for each
for each  and for all
and for all  where
where  denotes the segment joining
denotes the segment joining  and
and  ; that is,
; that is,  .
.
Our objective in this paper is to introduce the concept of weakly quasi-nonexpansive mappings with respect to a sequence. Mainly, we establish some convergence theorems of a sequence in complete metric spaces. These theorems generalize and improve [8, Theorems 2.1 and 2.2], of [7, Theorems 1.1 and  ], [5, Theorem 3.1], and [6, Proposition 1.1].
], [5, Theorem 3.1], and [6, Proposition 1.1].
2. Main Result
In this section, we introduce the concept of weak quasi-nonexpansiveness of a mapping with respect to a sequence that generalizes quasi-nonexpansiveness of a mapping with respect to a sequence in [8]. We give a lemma and a counterexample to show the relation between our new concept; the previous one appeared in [8] and a monotonically decreasing sequence  .
.
Definition 2.1.
Let  be a metric space and let
be a metric space and let  be a sequence in
be a sequence in  . Assume that
. Assume that  is a mapping with
is a mapping with  satisfying
satisfying  . Thus, for a given
. Thus, for a given  there is a
there is a  such that
such that  .
.  is called weakly quasi-nonexpansive with respect to
is called weakly quasi-nonexpansive with respect to  if for each
if for each  there exists a
there exists a  such that for all
such that for all  with
with  ,
,  .
.
We state the following lemma without proof.
Lemma 2.2.
Let  be a metric space and,
be a metric space and,  be a sequence in
be a sequence in  . Assume that
. Assume that  is a mapping with
is a mapping with  satisfying
satisfying  . If
. If  is quasi-nonexpansive with respect to
is quasi-nonexpansive with respect to  , then
, then
(A) is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  ;
;
(B) is a monotonically decreasing sequence in
is a monotonically decreasing sequence in  .
.
The following example shows that the converse of Lemma 2.2 may not be true.
Example 2.3.
Let  be endowed with the Euclidean metric
be endowed with the Euclidean metric  . We define the map
. We define the map  by
by  for each
for each  . Assume that
. Assume that  . Then
. Then

Given  , there exists
, there exists  such that for all
such that for all  with
with  , there exists
, there exists  ,
,

Thus,  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  . But,
. But,  is not quasi-nonexpansive with respect to
is not quasi-nonexpansive with respect to  (Indeed, there exists
(Indeed, there exists  such that for all
such that for all  ,
,  ). Furthermore, the sequence
). Furthermore, the sequence  is monotonically decreasing in
is monotonically decreasing in  .
.
Before stating the main theorem, let us introduce the following lemma without proof.
Lemma 2.4.
Let  be a metric space and let
be a metric space and let  be a sequence in
be a sequence in  . Assume that
. Assume that  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  with
with  satisfying
satisfying  . Then,
. Then,  is a Cauchy sequence.
is a Cauchy sequence.
Now, we give the main theorem without proof in the following way.
Theorem 2.5.
Let  be a sequence in a subset
be a sequence in a subset  of a metric space
of a metric space  and let
and let  be a map such that
be a map such that  . Then
. Then
(a) if
if  converges to a point in
converges to a point in  ;
;
(b) converges to a point in
converges to a point in  if
if  ,
,  is a closed set,
is a closed set,  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  , and
, and  is complete.
is complete.
As corollaries of Theorem 2.5, we have the following.
Corollary 2.6.
For each  , let
, let  be a sequence in a subset
be a sequence in a subset  of a metric space
of a metric space  and let
and let  be a map such that
be a map such that  . Then
. Then
(a) if
if  converges to a point in
converges to a point in  ;
;
(b) converges to a point in
converges to a point in  if
if  ,
,  is a closed set,
is a closed set,  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  and
and  is complete.
is complete.
Corollary 2.7.
For each  , let
, let  be a sequence in a subset
be a sequence in a subset  of a normed space
of a normed space  and let
and let  be a map such that
be a map such that  . Then
. Then
(a) if
if  converges to a point in
converges to a point in  ;
;
(b) converges to a point in
converges to a point in  if
if  ,
,  is a closed set,
is a closed set,  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  , and
, and  is a Banach space.
is a Banach space.
Corollary 2.8.
For each  , let
, let  be a sequence in a subset
be a sequence in a subset  of a normed space
of a normed space  and let
and let  be a map such that
be a map such that  . Then
. Then
(a) if
if  converges to a point in
converges to a point in  ;
;
(b) converges to a point in
converges to a point in  if
if  ,
,  is a closed set,
is a closed set,  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  , and
, and  is a Banach space.
is a Banach space.
Remark 2.9.
-
(I)
Theorem 2.5 generalizes and improves [8, Theorem 2.1] since
 is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to 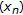 instead of
instead of  being quasi-nonexpansive with respect to
being quasi-nonexpansive with respect to 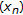 .
. -
(II)
Corollary 2.6 generalizes and improves [7, Theorem 1.1 page 462] for some reasons. These reasons are the following:
(1)the closedness of  is superfluous;
is superfluous;
(2) is closed instead of
is closed instead of  being continuous;
being continuous;
(3) is a complete metric space instead of
is a complete metric space instead of  is a Banach space;
is a Banach space;
(4) is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  in lieu of
in lieu of  being quasi-nonexpansive.
being quasi-nonexpansive.
-
(III)
Corollary 2.7 (resp. Corollary 2.8) generalizes and improves [7, Theorem
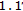 page 469] (resp. of [5, Theorem 3.1 page 98]) since the reasons (1) and (2) in (II) hold and
page 469] (resp. of [5, Theorem 3.1 page 98]) since the reasons (1) and (2) in (II) hold and
the convexity of  in Theorem 1.1
in Theorem 1.1 is superfluous;
is superfluous;
 is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  (resp.
(resp.  ) instead of
) instead of  being quasi-nonexpansive.
being quasi-nonexpansive.
-
(IV)
If we take
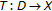 instead of
instead of 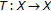 ,
,  is closed in lieu of
is closed in lieu of 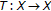 being continuous and
being continuous and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to 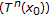 in lieu of
in lieu of  being quasi-nonexpansive, then Corollary 2.6 generalizes and improves Kirk [6, Proposition 1.1].
being quasi-nonexpansive, then Corollary 2.6 generalizes and improves Kirk [6, Proposition 1.1].
In the light of Lemma 2.2 and Example 2.3, we state the following theorem.
Theorem 2.10.
Let  be a sequence in a subset
be a sequence in a subset  of a complete metric space
of a complete metric space  and
and  be a map such that
be a map such that  is a closed set. Assume that
is a closed set. Assume that
(i) is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  ;
;
(ii) is a monotonically decreasing sequence in
is a monotonically decreasing sequence in  ;
;
(iii) ;
;
(iv)if the sequence  satisfies
satisfies  , then
, then

Then  converges to a point in
converges to a point in  .
.
Proof.
From the boundedness from below by zero of the sequence  and (ii), we obtain that
and (ii), we obtain that  exists. So, from (iii) and (iv), we have that
exists. So, from (iii) and (iv), we have that  or
or  . Then
. Then  (see, [18, page 37]). Therefore, by Theorem 2.5(b), the sequence
(see, [18, page 37]). Therefore, by Theorem 2.5(b), the sequence  converges to a point in
converges to a point in  .
.
Corollary 2.11.
For each  , let
, let  be a sequence in a subset
be a sequence in a subset  of a complete metric space
of a complete metric space  and let
and let  be a map such that
be a map such that  is a closed set. Assume that
is a closed set. Assume that
(i) is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  ;
;
(ii) is a monotonically decreasing sequence in
is a monotonically decreasing sequence in  ;
;
(iii) ;
;
(iv)if the sequence  satisfies
satisfies  , then
, then

Then  converges to a point in
converges to a point in  .
.
Corollary 2.12.
For each  let
let  be a sequence in a subset
be a sequence in a subset  of a Banach space
of a Banach space  and let
and let  be a map such that
be a map such that  is a closed set. Assume that
is a closed set. Assume that
(i) is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  ;
;
(ii) is a monotonically decreasing sequence in
is a monotonically decreasing sequence in  ;
;
(iii) ;
;
(iv)if the sequence  satisfies
satisfies  , then
, then

Then  converges to a point in
converges to a point in  .
.
Corollary 2.13.
For each  , let
, let  be a sequence in a subset
be a sequence in a subset  of a Banach space
of a Banach space  and let
and let  be a map such that
be a map such that  is a closed set. Assume that
is a closed set. Assume that
(i) is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  ;
;
(ii) is a monotonically decreasing sequence in
is a monotonically decreasing sequence in  ;
;
(iii) ;
;
(iv)if the sequence  satisfies
satisfies  , then
, then

Then  converges to a point in
converges to a point in  .
.
Remark 2.14.
From Lemma 2.2, we find that [8, Theorem 2.2] is a special case of Theorem 2.10. Also, Corollary 2.11 generalizes and improves [7, Theorem 1.2 page 464] for the same reasons in Remark 2.9(II).
We establish another consequence of Theorem 2.5 as follows.
Theorem 2.15.
Let  be a sequence in a subset
be a sequence in a subset  of a complete metric space
of a complete metric space  . Furthermore, let
. Furthermore, let  be a mapping such that
be a mapping such that  is a closed set. Assume that the conditions (i) and (ii) in Theorem 2.10 hold and
is a closed set. Assume that the conditions (i) and (ii) in Theorem 2.10 hold and
(iii)the sequence  contains a convergent subsequence
contains a convergent subsequence  converging to
converging to  such that there exists a continuous mapping
such that there exists a continuous mapping  satisfying
satisfying  and
and  for some
for some  .
.
Then  and
and  .
.
Proof.
From (ii), one can deduce that  exists, say equal
exists, say equal  . Suppose that
. Suppose that  does not belong to
does not belong to  . So, we have from (iii)
. So, we have from (iii) that for some
that for some  ,
,

This contradiction implies that  . Then,
. Then,

From Theorem 2.5(b), we obtain that  .
.
Corollary 2.16.
For each  , let
, let  be a sequence in a subset
be a sequence in a subset  of a complete metric space
of a complete metric space  . Furthermore, let
. Furthermore, let  be a mapping such that
be a mapping such that  is a closed set. Assume that the conditions (i) and (ii) in Corollary 2.11 hold and
is a closed set. Assume that the conditions (i) and (ii) in Corollary 2.11 hold and
(iii)the sequence  contains a convergent subsequence
contains a convergent subsequence  converging to
converging to  such that there exists a continuous mapping
such that there exists a continuous mapping  satisfying
satisfying  and
and  for some
for some  .
.
Then  and
and  .
.
Corollary 2.17.
For each  , let
, let  be a sequence in a subset
be a sequence in a subset  of a complete metric space
of a complete metric space  . Furthermore, let
. Furthermore, let  be a mapping such that
be a mapping such that  is a closed set. Assume that the conditions (i) and (ii) in Corollary 2.12 hold and
is a closed set. Assume that the conditions (i) and (ii) in Corollary 2.12 hold and
(iii)the sequence  contains a convergent subsequence
contains a convergent subsequence  converging to
converging to  such that there exists a continuous mapping
such that there exists a continuous mapping  satisfying
satisfying  and
and  for some
for some  .
.
Then  and
and  .
.
Corollary 2.18.
For each  , let
, let  be a sequence in a subset
be a sequence in a subset  of a complete metric space
of a complete metric space  . Furthermore, let
. Furthermore, let  be a mapping such that
be a mapping such that  is a closed set. Assume that the conditions (i) and (ii) in Corollary 2.13 hold and
is a closed set. Assume that the conditions (i) and (ii) in Corollary 2.13 hold and
(iii)the sequence  contains a convergent subsequence
contains a convergent subsequence  converging to
converging to  such that there exists a continuous mapping
such that there exists a continuous mapping  satisfying
satisfying  and
and  for some
for some  .
.
Then  and
and  .
.
Remark 2.19.
Theorem 1.3 in [7] is a special case of Corollary 2.16 for the same reasons in Remark 2.9(II) and for the generalization of the conditions (1.6) and (1.7) in [7, Theorem 1.3] to the condition (iii) in Corollary 2.16.
in Corollary 2.16.
From [17, Corollary 2.4] and Theorem 2.5(b), one can prove the following theorem.
Theorem 2.20.
Let  be a mapping of a complete metric space
be a mapping of a complete metric space  satisfying
satisfying
(i) for some
for some  and for all
and for all  ;
;
(ii) for some
for some  and for all
and for all  ;
;
(iii) is an r.g.i. on
is an r.g.i. on  ;
;
(iv) is a sequence in
is a sequence in  such that
such that  and
and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  .
.
Then  converges to a point in
converges to a point in  .
.
Corollary 2.21.
Let  be a mapping of a complete metric space
be a mapping of a complete metric space  satisfying
satisfying
(i) for some
for some  and for all
and for all  ;
;
(ii) for some
for some  and for all
and for all  ;
;
(iii) is an r.g.i. on
is an r.g.i. on  ;
;
(iv) is a sequence satisfying
is a sequence satisfying  for each
for each  and
and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  .
.
Then  converges to a point in
converges to a point in  .
.
Corollary 2.22.
Let  be a mapping of a Banach space
be a mapping of a Banach space  satisfying
satisfying
(i) for some
for some  and for all
and for all  ;
;
(ii) for some
for some  and for all
and for all  ;
;
(iii) is an r.g.i. on
is an r.g.i. on  ;
;
(iv) is a sequence in
is a sequence in  such that
such that  for each
for each  and
and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  .
.
Then  converges to a point in
converges to a point in  .
.
Corollary 2.23.
Let  be a mapping of a Banach space
be a mapping of a Banach space  satisfying
satisfying
(i) for some
for some  and for all
and for all  ;
;
(ii) for some
for some  and for all
and for all  ;
;
(iii) is an r.g.i. on
is an r.g.i. on  ;
;
(iv) is a sequence in
is a sequence in  such that
such that  for each
for each  and
and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  .
.
Then  converges to a point in
converges to a point in  .
.
Theorem 2.24.
Let  be a bounded closed convex subset of a Banach space
be a bounded closed convex subset of a Banach space  Suppose that
Suppose that  satisfies
satisfies
(i) is directionally nonexpansive on
is directionally nonexpansive on 
(ii) for some
for some  and for all
and for all  ;
;
(iii) is an r.g.i. on
is an r.g.i. on  ;
;
(iv) satisfies
satisfies  and
and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  .
.
Then  converges to a point in
converges to a point in  .
.
Proof.
The conclusion is obtained by combining [17, Theorem 3.3] and Theorem 2.5(b).
Corollary 2.25.
Let  be a bounded closed convex subset of a Banach space
be a bounded closed convex subset of a Banach space  Suppose that
Suppose that  satisfies
satisfies
(i) is directionally nonexpansive on
is directionally nonexpansive on  ;
;
(ii) for some
for some  and for all
and for all  ;
;
(iii) is an r.g.i. on
is an r.g.i. on  ;
;
(iv) for each
for each  satisfies
satisfies  and
and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  .
.
Then  converges to a point in
converges to a point in  .
.
Corollary 2.26.
Let  be a bounded closed convex subset of a Banach space
be a bounded closed convex subset of a Banach space  . Suppose that
. Suppose that  satisfies
satisfies
(i) is directionally nonexpansive on
is directionally nonexpansive on  ;
;
(ii) for some
for some  and for all
and for all  ;
;
(iii) is an r.g.i. on
is an r.g.i. on  ;
;
(iv) for each
for each  satisfies
satisfies  and
and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  .
.
Then  converges to a point in
converges to a point in  .
.
Corollary 2.27.
Let  be a bounded closed convex subset of a Banach space
be a bounded closed convex subset of a Banach space  . Suppose that
. Suppose that  satisfies
satisfies
(i) is directionally nonexpansive on
is directionally nonexpansive on  ;
;
(ii) for some
for some  and for all
and for all  ;
;
(iii) is an r.g.i. on
is an r.g.i. on  ;
;
(iv) for each
for each  satisfies
satisfies  and
and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to  .
.
Then  converges to a point in
converges to a point in  .
.
Remark 2.28.
It is worth to mention that Corollaries 2.12, 2.13, 2.17, 2.18, 2.21–2.23, 2.25–2.27 are new results.
References
Tricomi F: Un teorema sulla convergenza delle successioni formate della successive iterate di una funzione di una variable reale. Giornale di Matematiche di Battaglini 1916, 54: 1–9.
Das KM, Singh SP, Watson B: A note on Mann iteration for quasinonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 1981,5(6):675–676. 10.1016/0362-546X(81)90083-3
Dotson WG Jr.: On the Mann iterative process. Transactions of the American Mathematical Society 1970, 149: 65–73. 10.1090/S0002-9947-1970-0257828-6
Ghosh MK, Debnath L: Approximation of the fixed points of quasi-nonexpansive mappings in a uniformly convex Banach space. Applied Mathematics Letters 1992,5(3):47–50. 10.1016/0893-9659(92)90037-A
Ghosh MK, Debnath L: Convergence of Ishikawa iterates of quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 1997,207(1):96–103. 10.1006/jmaa.1997.5268
Kirk WA: Remarks on approximation and approximate fixed points in metric fixed point theory. Annales Universitatis Mariae Curie-Skłodowska. Sectio A 1997,51(2):167–178.
Petryshyn WV, Williamson TE Jr.: Strong and weak convergence of the sequence of successive approximations for quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 1973, 43: 459–497. 10.1016/0022-247X(73)90087-5
Ahmed MA, Zeyada FM: On convergence of a sequence in complete metric spaces and its applications to some iterates of quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 2002,274(1):458–465. 10.1016/S0022-247X(02)00242-1
Qihou L: Iterative sequences for asymptotically quasi-nonexpansive mappings. Journal of Mathematical Analysis and Applications 2001,259(1):1–7. 10.1006/jmaa.2000.6980
Qihou L: Iterative sequences for asymptotically quasi-nonexpansive mappings with error member. Journal of Mathematical Analysis and Applications 2001,259(1):18–24. 10.1006/jmaa.2000.7353
Qihou L: Iteration sequences for asymptotically quasi-nonexpansive mapping with an error member of uniform convex Banach space. Journal of Mathematical Analysis and Applications 2002,266(2):468–471. 10.1006/jmaa.2001.7629
Zeidler E: Nonlinear Functional Analysis and Its Applications. I: Fixed-Point Theorems. Springer, New York, NY, USA; 1986:xxi+897.
Ishikawa S: Fixed points by a new iteration method. Proceedings of the American Mathematical Society 1974, 44: 147–150. 10.1090/S0002-9939-1974-0336469-5
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Kirk WA: Nonexpansive mappings and asymptotic regularity. Nonlinear Analysis: Theory, Methods & Applications 2000,40(1–8):323–332.
Angrisani M, Clavelli M: Synthetic approaches to problems of fixed points in metric space. Annali di Matematica Pura ed Applicata. Serie Quarta 1996, 170: 1–12. 10.1007/BF01758980
Kirk WA, Saliga LM: Some results on existence and approximation in metric fixed point theory. Journal of Computational and Applied Mathematics 2000,113(1–2):141–152. 10.1016/S0377-0427(99)00249-6
Royden HL: Real Analysis. The Macmillan, New York, NY, USA; 1963:xvi+284.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ahmed, M., Zeyada, F. Some Convergence Theorems of a Sequence in Complete Metric Spaces and Its Applications. Fixed Point Theory Appl 2010, 647085 (2009). https://doi.org/10.1155/2010/647085
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/647085
 is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to 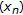 instead of
instead of  being quasi-nonexpansive with respect to
being quasi-nonexpansive with respect to 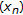 .
.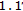 page 469] (resp. of [
page 469] (resp. of [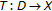 instead of
instead of 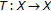 ,
,  is closed in lieu of
is closed in lieu of 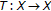 being continuous and
being continuous and  is weakly quasi-nonexpansive with respect to
is weakly quasi-nonexpansive with respect to 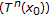 in lieu of
in lieu of  being quasi-nonexpansive, then Corollary 2.6 generalizes and improves Kirk [
being quasi-nonexpansive, then Corollary 2.6 generalizes and improves Kirk [