- Review Article
- Open access
- Published:
Normal Structure and Common Fixed Point Properties for Semigroups of Nonexpansive Mappings in Banach Spaces
Fixed Point Theory and Applications volume 2010, Article number: 580956 (2010)
Abstract
In 1965, Kirk proved that if  is a nonempty weakly compact convex subset of a Banach space with normal structure, then every nonexpansive mapping
is a nonempty weakly compact convex subset of a Banach space with normal structure, then every nonexpansive mapping  has a fixed point. The purpose of this paper is to outline various generalizations of Kirk's fixed point theorem to semigroup of nonexpansive mappings and for Banach spaces associated to a locally compact group.
has a fixed point. The purpose of this paper is to outline various generalizations of Kirk's fixed point theorem to semigroup of nonexpansive mappings and for Banach spaces associated to a locally compact group.
1. Introduction
A closed convex subset  of a Banach space
of a Banach space  has normal structure if for each bounded closed convex subset
has normal structure if for each bounded closed convex subset  of
of  which contains more than one point, there is a point
which contains more than one point, there is a point  which is not a diametral point of
which is not a diametral point of  that is,
that is,  where
where  the diameter of
the diameter of 
The set  is said to have fixed point property (FPP) if every nonexpansive mapping
is said to have fixed point property (FPP) if every nonexpansive mapping  has a fixed point. In [1], Kirk proved the following important celebrated result.
has a fixed point. In [1], Kirk proved the following important celebrated result.
Theorem 1.1 (Kirk [1]).
Let  be a Banach space, and
be a Banach space, and  a nonempty closed convex subset of
a nonempty closed convex subset of  If
If  is weakly compact and has normal structure, then
is weakly compact and has normal structure, then  has the FPP.
has the FPP.
As well known, compact convex subset of a Banach space  always has normal structure (see [2]). It was an open problem for over 15 years whether every weakly compact convex subset of
always has normal structure (see [2]). It was an open problem for over 15 years whether every weakly compact convex subset of  has normal structure. This problem was answered negatively by Alspach [3] when he showed that there is a weakly compact convex subset
has normal structure. This problem was answered negatively by Alspach [3] when he showed that there is a weakly compact convex subset  of
of  which does not have the fixed point property. In particular,
which does not have the fixed point property. In particular,  cannot have normal structure.
cannot have normal structure.
It is the purpose of this paper to outline the relation of normal structure and fixed point property for semigroup of nonexpansive mappings. This paper is organized as follows. In Section 3, we will focus on generalizations of Kirk's fixed point theorem to semigroups of nonexpansive mappings. In Section 4, we will discuss about fixed point properties and normal structure on Banach spaces associated to a locally compact group.
2. Some Preliminaries
All topologies in this paper are assumed to be Hausdorff. If  is a Banach space and
is a Banach space and  then
then  and
and  will denote the closure of
will denote the closure of  and the closed convex hull of
and the closed convex hull of  in
in  respectively.
respectively.
Let  be a Banach space and let
be a Banach space and let  a subset of
a subset of  A mapping
A mapping  from
from  into itself is said to be nonexpansive if
into itself is said to be nonexpansive if  for each
for each  A Banach space
A Banach space  is said to be uniformly convex if for each
is said to be uniformly convex if for each  there exists
there exists  such that
such that  for each
for each  satisfying
satisfying 
 and
and 
Let  be a semigroup,
be a semigroup,  the Banach space of bounded real valued functions on
the Banach space of bounded real valued functions on  with the supremum norm. Then a subspace
with the supremum norm. Then a subspace  of
of  is left (resp., right) translation invariant if
is left (resp., right) translation invariant if  (resp.,
(resp.,  for all
for all  where
where  and
and  ,
, 
A semitoplogical semigroup is a semigroup with Hausdorff topology such that for each
is a semigroup with Hausdorff topology such that for each  the mappings
the mappings  and
and  from
from  into
into  are continuous. Examples of semitopological semigroups include all topological groups, the set
are continuous. Examples of semitopological semigroups include all topological groups, the set  of all
of all  matrices with complex entries, matrix multiplication, and the usual topology, the unit ball of
matrices with complex entries, matrix multiplication, and the usual topology, the unit ball of  with weak
with weak -topology and pointwise multiplication, or
-topology and pointwise multiplication, or 
 the space of bounded linear operators on a Hilbert space
the space of bounded linear operators on a Hilbert space  with the weak
with the weak -topology and composition.
-topology and composition.
If  is a semitopological semigroup, we denote
is a semitopological semigroup, we denote  the closed subalgebra of
the closed subalgebra of  consisting of continuous functions. Let
consisting of continuous functions. Let  (resp.,
(resp.,  be the space of left (resp., right) uniformly continuous functions on
be the space of left (resp., right) uniformly continuous functions on  that is, all
that is, all  such that the mapping from
such that the mapping from  into
into  defined by
defined by  (resp.,
(resp.,  is continuous when
is continuous when  has the sup norm topology. Then as is known (see [4]),
has the sup norm topology. Then as is known (see [4]),  and
and  are left and right translation invariant closed subalgebras of
are left and right translation invariant closed subalgebras of  containing constants. Also let
containing constants. Also let  (resp.,
(resp.,  denote the space of almost periodic (resp., weakly almost periodic) functions
denote the space of almost periodic (resp., weakly almost periodic) functions  in
in  that is, all
that is, all  such that
such that  is relatively compact in the norm (resp., weak) topology of
is relatively compact in the norm (resp., weak) topology of  or equivalently
or equivalently  is relatively compact in the norm (resp., weak) topology of
is relatively compact in the norm (resp., weak) topology of  Then as is known [4, page 164],
Then as is known [4, page 164],  and
and  When
When  is a locally compact group, then
is a locally compact group, then  (see [4, page 167]).
(see [4, page 167]).
A semitopological semigroup  is left reversible if any two closed right ideals of
is left reversible if any two closed right ideals of  have nonvoid intersection.
have nonvoid intersection.
The class  of all left reversible semitopological semigroups includes trivially all semitopological semigroups which are algebraically groups, and all commuting semigroups.
of all left reversible semitopological semigroups includes trivially all semitopological semigroups which are algebraically groups, and all commuting semigroups.
The class  is closed under the following operations.
is closed under the following operations.
(a)If  and
and  is a continuous homomorphic image of
is a continuous homomorphic image of  then
then 
(b)Let  ,
,  and
and  be the semitopological semigroup consisting of the set of all functions
be the semitopological semigroup consisting of the set of all functions  on
on  such that
such that  ,
,  the binary operation defined by
the binary operation defined by  for all
for all  and
and  and the product topology. Then
and the product topology. Then 
(c)Let  be a semitopological semigroup and
be a semitopological semigroup and  ,
,  semitopological sub-semigroups of
semitopological sub-semigroups of  with the property that
with the property that  and, if
and, if  ,
,  then there exists
then there exists  such that
such that  If
If  for each
for each  then
then 
Let  be a nonempty set and
be a nonempty set and  a translation invariant subspace of
a translation invariant subspace of  containing constants. Then
containing constants. Then  is called a mean on
is called a mean on  if
if  As well known,
As well known,  is a mean on
is a mean on  if and only if
if and only if

for each 
Also  is called a left (resp., right) invariant mean if
is called a left (resp., right) invariant mean if  (resp.,
(resp.,  for all
for all 
Lemma 2.1.
Let  be a semitopological semigroup and
be a semitopological semigroup and  a left translation invariant subspace of
a left translation invariant subspace of  containing constants and which separates closed subsets of
containing constants and which separates closed subsets of  If
If  has a left invariant mean, then
has a left invariant mean, then  is left reversible.
is left reversible.
Proof.
Let  be a left invariant mean of
be a left invariant mean of  ,
,  and
and  disjoint nonempty closed right ideals of
disjoint nonempty closed right ideals of  By assumption, there exists
By assumption, there exists  such that
such that  on
on  and
and  on
on  Now if
Now if  then
then  So,
So,

But if  then
then  So
So  which is impossible.
which is impossible.
Corollary 2.2.
If  is normal and
is normal and  has a left invariant mean, then
has a left invariant mean, then  is left reversible.
is left reversible.
See [5] for details.
A discrete semigroup  is called left amenable [6] if
is called left amenable [6] if  has a left invariant mean. In particular every left amenable discrete semigroup is left reversible by Corollary 2.2. The semigroup
has a left invariant mean. In particular every left amenable discrete semigroup is left reversible by Corollary 2.2. The semigroup  is amenable if it is both left and right amenable. In this case, there is always an invariant mean on
is amenable if it is both left and right amenable. In this case, there is always an invariant mean on 
Remark 2.3.
Lemma 2.1 is not true without normality. Let  be a topological space which is regular and Hausdorff and
be a topological space which is regular and Hausdorff and  consists of constant functions only [7]. Define on
consists of constant functions only [7]. Define on  the multiplication
the multiplication  for all
for all  Let
Let  be fixed. Define
be fixed. Define  for all
for all  Then
Then  is a left invariant mean on
is a left invariant mean on  but
but  is not left reversible.
is not left reversible.
3. Generalizations of Kirk's Fixed Point Theorem
By a (nonlinear) submean on  we will mean a real-valued function
we will mean a real-valued function  on
on  satisfying the following properties:
satisfying the following properties:
(1) for every
for every 
(2) for every
for every  and
and 
(3)for 
 implies
implies 
(4) for every constant function
for every constant function 
Clearly every mean is a submean. See [8] for details.
If  is a semigroup and
is a semigroup and  is left translation invariant, a submean
is left translation invariant, a submean  on
on  is left subinvariant if
is left subinvariant if  for each
for each  and
and 
Let  be a semitopological semigroup,
be a semitopological semigroup,  a nonempty subset of a Banach space
a nonempty subset of a Banach space  then a representation
then a representation  of
of  as mappings from
as mappings from  into
into  is continuous if
is continuous if  defined by
defined by 

 is continuous when
is continuous when  has the product topology. It is called separately continuous if for each
has the product topology. It is called separately continuous if for each  and
and  the maps
the maps  from
from  into
into  and the map
and the map  from
from  into
into  are continuous.
are continuous.
Theorem 3.1.
Let  be a semitopological semigroup, let
be a semitopological semigroup, let  a nonempty weakly compact convex subset of a Banach space
a nonempty weakly compact convex subset of a Banach space  which has normal structure and let
which has normal structure and let  a continuous representation of
a continuous representation of  as nonexpansive self-mappings on
as nonexpansive self-mappings on  Suppose that
Suppose that  has a left subinvariant submean. Then
has a left subinvariant submean. Then  has a common fixed point in
has a common fixed point in 
Corollary 3.2.
Let  be a left reversible semitopological semigroup. Let
be a left reversible semitopological semigroup. Let  be a nonempty weakly compact convex subset of a Banach space
be a nonempty weakly compact convex subset of a Banach space  which has normal structure and let
which has normal structure and let  a continuous representation of
a continuous representation of  as nonexpansive self-mappings on
as nonexpansive self-mappings on  Then
Then  has a fixed point in
has a fixed point in 
Proof.
If  is left reversible, define
is left reversible, define  Then the proof of Lemma
Then the proof of Lemma  in [9] shows that
in [9] shows that  is a submean on
is a submean on  such that
such that  for all
for all  and
and  that is,
that is,  is left subinvariant.
is left subinvariant.
Note that since every compact convex set has normal structure, Corollary 3.2 implies the following.
Corollary 3.3 (DeMarr [10]).
Let  be a Banach space and
be a Banach space and  a nonempty compact convex subset of
a nonempty compact convex subset of  If
If  is a commuting family of nonexpansive mappings of
is a commuting family of nonexpansive mappings of  into
into  then the family
then the family  has a common fixed point in
has a common fixed point in 
Remark 3.4.
Theorem 3.1 is proved by Lau and Takahashi in [11]. Mitchell [12] generalized the theorems of DeMarr [10, page 1139] and Takahaski [13, page 384] by showing that if  is a nonempty compact convex subset of a Banach space and
is a nonempty compact convex subset of a Banach space and  is a left-reversible discrete semigroup of nonexpansive mappings from
is a left-reversible discrete semigroup of nonexpansive mappings from  into
into  then
then  contains a common fixed point for
contains a common fixed point for  Belluce and Kirk [14] also improved DeMarr's result in [10] and proved that if
Belluce and Kirk [14] also improved DeMarr's result in [10] and proved that if  is a nonempty weakly compact convex subset of a Banach space and if
is a nonempty weakly compact convex subset of a Banach space and if  has complete normal structure, then every family of commuting nonexpansive self-maps on
has complete normal structure, then every family of commuting nonexpansive self-maps on  has a common fixed point.
has a common fixed point.
This result was extended to the class of left reversible semitopological semigroup by Holmes and Lau in [15]. Corollary 3.2 is due to Lim [16] who showed that normal structure and complete normal structure are equivalent.
The following related theorem was also established in [15].
Theorem 3.5.
Let  be a left reversible semitopological semigroup, let
be a left reversible semitopological semigroup, let  a nonempty, bounded, closed convex subset of a Banach space
a nonempty, bounded, closed convex subset of a Banach space  and let
and let  a separately continuous representation of
a separately continuous representation of  as nonexpansive self-maps on
as nonexpansive self-maps on  If there is a nonempty compact subset
If there is a nonempty compact subset  and
and  such that
such that  commutes with all elements of
commutes with all elements of  and for each
and for each  the closure of the set
the closure of the set  contains a point of
contains a point of  then
then  contains a common fixed point of
contains a common fixed point of 
Let  be a semitopological semigroup and
be a semitopological semigroup and  is a nonempty subset of a Banach space
is a nonempty subset of a Banach space  and
and  a separately continuous representation of
a separately continuous representation of  as mappings from
as mappings from  into
into  We say that the representation is asymptotically nonexpansive if for each
We say that the representation is asymptotically nonexpansive if for each  there is a left ideal
there is a left ideal  such that
such that  for all
for all 
We also say that the representation has property (B) if for each  whenever a net
whenever a net 
 converges to
converges to  then the net
then the net  also converges to
also converges to  for each
for each 
Clearly condition (B) is automatically satisfied when  is commutative.
is commutative.
The semitopological semigroup  is right reversible if
is right reversible if

The following theorem is proved in [17].
Theorem 3.6.
Let  be a nonempty compact convex subset of a Banach space
be a nonempty compact convex subset of a Banach space  and
and  a right reversible semitopological semigroup. If
a right reversible semitopological semigroup. If  is a separately continuous asymptotically nonexpansive representation of
is a separately continuous asymptotically nonexpansive representation of  as mappings from
as mappings from  into
into  with property (B), then
with property (B), then  contains a common fixed point for
contains a common fixed point for 
The following example from [17] shows a simple situation where our fixed point theorem applies, but DeMarr's fixed point theorem does not.
Let  be the closed unit disc in
be the closed unit disc in  with polar coordinates and the usual Euclidean norm. Define continuous mappings
with polar coordinates and the usual Euclidean norm. Define continuous mappings  from
from  into
into  by
by

Then the semigroup of continuous mappings from  to
to  generated by
generated by  and
and  under usual composition is commutative and asymptotically nonexpansive. However, the action of
under usual composition is commutative and asymptotically nonexpansive. However, the action of  (or any ideal of
(or any ideal of  on
on  is not nonexpansive.
is not nonexpansive.
Open Problem 1.
Can right reversibility of  and property (B) in Theorem 3.6 be replaced by amenability of
and property (B) in Theorem 3.6 be replaced by amenability of 
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  Then
Then  has the fixed point property for nonexpansive mappings if every nonexpansive mapping
has the fixed point property for nonexpansive mappings if every nonexpansive mapping  has a fixed point;
has a fixed point;  has the onlyconditional fixed point property for nonexpansive mappings if every nonexpansive mapping
has the onlyconditional fixed point property for nonexpansive mappings if every nonexpansive mapping  satisfies either
satisfies either  has no fixed point in
has no fixed point in  or
or  has a fixed point in every nonempty bounded closed convex
has a fixed point in every nonempty bounded closed convex  -invariant subset of
-invariant subset of  For commuting family of nonexpansive mappings, the following is a remarkable common fixed point property due to Bruck [18].
For commuting family of nonexpansive mappings, the following is a remarkable common fixed point property due to Bruck [18].
Theorem 3.7.
Let  be a Banach space and
be a Banach space and  a nonempty closed convex subset of
a nonempty closed convex subset of  If
If  has both the fixed point property and the conditional fixed point property for nonexpansive mappings, then for any commuting family
has both the fixed point property and the conditional fixed point property for nonexpansive mappings, then for any commuting family  of nonexpansive mappings of
of nonexpansive mappings of  into
into  there is a common fixed point for
there is a common fixed point for 
Theorem 3.7 was proved by Belluce and Kirk [19] when  is finite and
is finite and  is weakly compact and has normal structure, by Belluce and Kirk [14] when
is weakly compact and has normal structure, by Belluce and Kirk [14] when  is weakly compact and has complete normal structure, Browder [20] when
is weakly compact and has complete normal structure, Browder [20] when  is uniformly convex and
is uniformly convex and  is bounded, Lau and Holmes [15] when
is bounded, Lau and Holmes [15] when  is left reversible and
is left reversible and  is compact, and finally by Lim [16] when
is compact, and finally by Lim [16] when  is left reversible and
is left reversible and  is weakly compact and has normal structure.
is weakly compact and has normal structure.
Open Problem 2 (Bruck [18]).
Can commutativity of  be replaced by left reversibility?
be replaced by left reversibility?
The answer to Problem 2 is not known even when the semigroup is left amenable.
Let  be a compact right topological semigroup, that is, a semigroup and a compact Hausdorff topological space such that for each
be a compact right topological semigroup, that is, a semigroup and a compact Hausdorff topological space such that for each  the mapping
the mapping  from
from  into
into  is continuous. In this case,
is continuous. In this case,  must contain minimal left ideals. Any minimal left ideal in
must contain minimal left ideals. Any minimal left ideal in  is closed and any two minimal left ideals of
is closed and any two minimal left ideals of  are homeomorphic and algebraically isomorphic.
are homeomorphic and algebraically isomorphic.
Let  be a nonempty weakly compact convex subset of a Banach space
be a nonempty weakly compact convex subset of a Banach space  Let
Let  be a representation of a semigroup
be a representation of a semigroup  as nonexpansive and weak-weak continuous mappings from
as nonexpansive and weak-weak continuous mappings from  into
into  Let
Let  be the closure of
be the closure of  in the product space
in the product space  weak)
weak) Then
Then  is a compact right topological semigroup consisting of nonexpansive mappings from
is a compact right topological semigroup consisting of nonexpansive mappings from  into
into  Further, for any
Further, for any  there exists a sequence
there exists a sequence  of convex combination of operators from
of convex combination of operators from  such that
such that  for every
for every  See [21] for details.
See [21] for details.
 is called the enveloping semigroup of
is called the enveloping semigroup of 
Theorem 3.8.
Let  be a nonempty weakly compact convex subset of a Banach space,
be a nonempty weakly compact convex subset of a Banach space,  and
and  has normal structure. Let
has normal structure. Let  be a representation of a semigroup as norm nonexpansive and weakly continuous mappings from
be a representation of a semigroup as norm nonexpansive and weakly continuous mappings from  into
into  and let
and let  be the enveloping semigroup of
be the enveloping semigroup of  Let
Let  be a minimal left ideal of
be a minimal left ideal of  and let
and let  a minimal
a minimal  -invariant closed convex subset of
-invariant closed convex subset of  Then there exists a nonempty weakly closed subset
Then there exists a nonempty weakly closed subset  of
of  such that
such that  is constant on
is constant on 
Corollary 3.9.
Let  and
and  as in Theorem 3.8. Then there exist
as in Theorem 3.8. Then there exist  and
and  such that
such that  for every
for every 
Proof.
Pick  and
and  of the above theorem.
of the above theorem.
Remark 3.10.
If  is commutative, then for any
is commutative, then for any  and
and 
 that is,
that is,  is in fact a common fixed point for
is in fact a common fixed point for  (and, hence, for
(and, hence, for  Note that if
Note that if  is norm compact, the weak and norm topology agree on
is norm compact, the weak and norm topology agree on  Hence every nonexpansive mapping from
Hence every nonexpansive mapping from  into
into  must be weakly continuous. Therefore, Corollary 3.9 improves the fixed point theorem of DeMarr [10] for commuting semigroups of nonexpansive mappings on compact convex sets.
must be weakly continuous. Therefore, Corollary 3.9 improves the fixed point theorem of DeMarr [10] for commuting semigroups of nonexpansive mappings on compact convex sets.
The above theorem proved in [21] provides a new approach using enveloping semigroups in the study of common fixed point of a semigroup of nonexpansive mappings on a weakly compact convex subset of a Banach space.
Open Problem 3.
Can the above technique applied to give a proof of Lim's fixed point theorem for left reversible semigroup in [16].
The following generalization of DeMarr's fixed point theorem was proved in [22].
Theorem 3.11.
Let  a be semitopological semigroup.
a be semitopological semigroup.
If  has a left invariant mean, then
has a left invariant mean, then  has the following fixed point property. Whenever
has the following fixed point property. Whenever  is a separately continuous representation of
is a separately continuous representation of  as nonexpansive self-mappings on a compact convex subset
as nonexpansive self-mappings on a compact convex subset  of a Banach space, then
of a Banach space, then  contains a common fixed point for
contains a common fixed point for 
Quite recently the Lau and Zhang [23] are able to establish the following related fixed point property.
Theorem 3.12.
Let  be a separable semitopological semigroup. If
be a separable semitopological semigroup. If  has a left invariant mean, then
has a left invariant mean, then  has the following fixed point property:
has the following fixed point property:
Whenever  is a continuous representation of
is a continuous representation of  as nonexpansive self-mappings on a weakly compact convex subset
as nonexpansive self-mappings on a weakly compact convex subset  of a Banach space
of a Banach space  such that the closure of
such that the closure of  in
in  with the product of weak topology consists entirely of continuous functions, then
with the product of weak topology consists entirely of continuous functions, then  contains a common fixed point of
contains a common fixed point of 
Remark 3.13.
-
(a)
The converse of Theorem 3.12 also holds when
 has an identity by considering
has an identity by considering 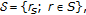 the semigroup of right translations, on the weakly compact convex sets
the semigroup of right translations, on the weakly compact convex sets 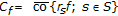 for each
for each 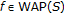 (see [24]).
(see [24]). -
(b)
When
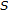 is a discrete semigroup, the following implication diagram is known:
is a discrete semigroup, the following implication diagram is known: 
The implication "
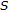 is left reversible
is left reversible  has a
has a  " for any semitopological semigroup was established in [22]. During the 1984 Richmond, Virginia conference on analysis on semigroups, T. Mitchell [12] gave two examples to show that for discrete semigroups "
" for any semitopological semigroup was established in [22]. During the 1984 Richmond, Virginia conference on analysis on semigroups, T. Mitchell [12] gave two examples to show that for discrete semigroups "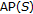 has
has 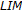 "
"  "
"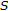 is left reversible" (see [25] or [23]). The implication "
is left reversible" (see [25] or [23]). The implication "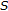 is left reversible
is left reversible  has
has 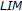 " for discrete semigroups was proved by Hsu [26]. Recently, it is shown in [23] that if
" for discrete semigroups was proved by Hsu [26]. Recently, it is shown in [23] that if 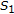 is the bicyclic semigroup generated by
is the bicyclic semigroup generated by  such that
such that  is the unit of
is the unit of 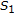 and
and 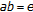 and
and 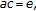 then
then  has a
has a  but
but  is not left reversible. Also if
is not left reversible. Also if 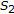 is the bicyclic semigroup generated by
is the bicyclic semigroup generated by  where
where  is the unit element and
is the unit element and 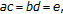 then
then  has a
has a  but
but 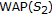 does not have a
does not have a 
The following is proved in [5] (see also [27]).
Theorem 3.14.
Let  be a left reversible discrete semigroup. Then
be a left reversible discrete semigroup. Then  has the following fixed point property.
has the following fixed point property.
Whenever  is a representation of
is a representation of  as norm nonexpansive weak
as norm nonexpansive weak -weak
-weak continuous mappings of a norm-separable weak
continuous mappings of a norm-separable weak -compact convex subset
-compact convex subset  of a dual Banach space
of a dual Banach space  into
into  then
then  contains a common fixed point for
contains a common fixed point for 
It can be shown that the following fixed point property on a discrete semigroup  implies that
implies that  is left amenable.
is left amenable.
(G) Whenever  is a representation of
is a representation of  as norm nonexpansive weak
as norm nonexpansive weak -weak
-weak continuous mappings of a weak
continuous mappings of a weak -compact convex subset
-compact convex subset  of a dual Banach space
of a dual Banach space  into
into  then
then  contains a common fixed point for
contains a common fixed point for 
Open Problem 4.
Does left amenability of  imply
imply 
Other related results for this section can also be found in [9, 28–38].
4. Normal Structure in Banach Spaces Associated to Locally Compact Groups
A Banach space has weak-normal structure if every nontrivial weakly compact convex subset has normal structure. If the Banach space is also a dual space then it has weak -normal structure if every nontrivial weak
-normal structure if every nontrivial weak compact convex subset has normal structure. It is clear that a dual Banach space has weak-normal structure whenever it has weak
compact convex subset has normal structure. It is clear that a dual Banach space has weak-normal structure whenever it has weak -normal structure.
-normal structure.
A [dual] Banach space  is said to have the weak-fixed point property (weak-FPP) [(FPP
is said to have the weak-fixed point property (weak-FPP) [(FPP if for every weakly [weak
if for every weakly [weak compact convex subset
compact convex subset  of
of  and for every nonexpansive
and for every nonexpansive  has a fixed point in
has a fixed point in  Kirk proved that if
Kirk proved that if  has weak-normal structure then
has weak-normal structure then  has property FPP [1]. Subsequently, Lim [39] proved that a dual Banach space has property FPP
has property FPP [1]. Subsequently, Lim [39] proved that a dual Banach space has property FPP whenever it has weak
whenever it has weak -normal structure.
-normal structure.
A Banach space  is said to have the Kadec-Klee property (KK) if whenever
is said to have the Kadec-Klee property (KK) if whenever  is a sequence in the unit ball of
is a sequence in the unit ball of  that converges weakly to
that converges weakly to  and
and  where
where

then  (see [40]).
(see [40]).
For dual Banach spaces, we have the similar properties replacing weak converges by weak converges.
converges.
A Banach space  is said to have the uniformly Kadec-Klee property (UKK) if for every
is said to have the uniformly Kadec-Klee property (UKK) if for every  there is a
there is a  such that whenever
such that whenever  is a sequence in the unit ball of
is a sequence in the unit ball of  converging weakly to
converging weakly to  and
and  then
then  This property was introduced by Huff [40] who showed that property UKK is strictly stronger than property KK. van Dulst and Sims showed that a Banach space with property UKK has property weak FPP [41].
This property was introduced by Huff [40] who showed that property UKK is strictly stronger than property KK. van Dulst and Sims showed that a Banach space with property UKK has property weak FPP [41].
It is natural to define a property similar to UKK by replacing the weak convergence by weak convergence in UKK and calling it UKK
convergence in UKK and calling it UKK However, van Dulst and Sims found that the following definition is more useful.
However, van Dulst and Sims found that the following definition is more useful.
A dual Banach space  has property UKK
has property UKK if for every
if for every  there is a
there is a  such that whenever
such that whenever  is a subset of the closed unit ball of
is a subset of the closed unit ball of  containing a sequence
containing a sequence  with
with  then there is an
then there is an  in weak
in weak -closure
-closure  such that
such that 
They proved that a dual Banach space with property UKK has property FPP
has property FPP [41]. Moreover, they observed that if the dual unit ball is weak
[41]. Moreover, they observed that if the dual unit ball is weak sequentially compact then property UKK
sequentially compact then property UKK as defined above, is equivalent to the condition obtained from UKK by replacing weak convergence by weak
as defined above, is equivalent to the condition obtained from UKK by replacing weak convergence by weak convergence.
convergence.
We now summarize the various properties defined above by

(where n.s. = normal structure).
Let  Then, as noted by Huff [40],
Then, as noted by Huff [40],  is reflexive and has property KK but not UKK.
is reflexive and has property KK but not UKK.
Let  be a locally compact Hausdorff space, and
be a locally compact Hausdorff space, and  the space of bounded continuous complex-valued functions defined on
the space of bounded continuous complex-valued functions defined on  with the supremum norm. Let
with the supremum norm. Let  be the subspace of
be the subspace of  consisting of functions "vanishing at infinity," and
consisting of functions "vanishing at infinity," and  be the space of bounded regular Borel measure on
be the space of bounded regular Borel measure on  with the variation norm. Let
with the variation norm. Let  be the subspace of
be the subspace of  consisting of the discrete measures on
consisting of the discrete measures on  It is well known that the dual of
It is well known that the dual of  can be identified with
can be identified with  and that
and that  is isometrically isomorphic to
is isometrically isomorphic to 
Lennard [42] proved the following theorem.
Theorem 4.1.
Let  be a Hilbert space. Then
be a Hilbert space. Then  the trace class operators on
the trace class operators on  has the property UKK
has the property UKK and has FPP
and has FPP when regarded as the dual space of
when regarded as the dual space of  the
the  -algebra of compact operator on
-algebra of compact operator on 
Theorem 4.2.
Let  be a locally compact group. Then the following statements are equivalent.
be a locally compact group. Then the following statements are equivalent.
(1) is discrete.
is discrete.
(2) is isometrically isomorphic to
is isometrically isomorphic to 
(3) has property UKK
has property UKK .
.
(4) has property KK
has property KK .
.
(5)Weak convergence and weak convergence of sequences agree on the unit sphere of
convergence and weak convergence of sequences agree on the unit sphere of 
(6) has weak
has weak normal structure.
normal structure.
(7) has property FPP
has property FPP .
.
Theorem 4.3.
Let  be a locally compact group. Then the group algebra
be a locally compact group. Then the group algebra  has the weak fixed point property for left reversible semigroups if and only if
has the weak fixed point property for left reversible semigroups if and only if  is discrete.
is discrete.
Theorem 4.4.
Let  be a locally compact group. Let
be a locally compact group. Let  be a
be a  -subalgebra of
-subalgebra of  containing
containing  and the constants. Then the following statements are equivalent.
and the constants. Then the following statements are equivalent.
(1) is finite.
is finite.
(2) has property UKK
has property UKK
(3) has property KK
has property KK
(4)Weak convergence and weak convergence for sequences agree on the unit sphere of
convergence and weak convergence for sequences agree on the unit sphere of 
(5) has weak
has weak -normal structure.
-normal structure.
Theorem 4.5.
Let  be a locally compact group. Then
be a locally compact group. Then
(1)Weak convergence and weak convergence for sequences agree on the unit sphere of
convergence and weak convergence for sequences agree on the unit sphere of  if and only if
if and only if  is discrete.
is discrete.
(2) has weak
has weak -normal structure if and only if
-normal structure if and only if  is finite.
is finite.
Let  be a locally compact group. We define
be a locally compact group. We define  the group
the group  -algebra of
-algebra of  to be the completion of
to be the completion of  with respect to the norm
with respect to the norm

where the supremum is taken over all nondegenerate representations  of
of  as an algebra of bounded operator on a Hilbert space. Let
as an algebra of bounded operator on a Hilbert space. Let  be the Banach space of bounded continuous complex-valued function on
be the Banach space of bounded continuous complex-valued function on  with the supremum norm. Denote the set of continuous positive definite functions on
with the supremum norm. Denote the set of continuous positive definite functions on  by
by  and the set of continuous functions on
and the set of continuous functions on  with compact support by
with compact support by  Define the Fourier-Stieltjes algebra of
Define the Fourier-Stieltjes algebra of  denoted by
denoted by  to be the linear span of
to be the linear span of  The Fourier algebra of
The Fourier algebra of  denoted by
denoted by  is defined to be the closed linear span of
is defined to be the closed linear span of  Finally, let
Finally, let  be the left regular representation of
be the left regular representation of  that is, for each
that is, for each 
 is the bounded operator in
is the bounded operator in  defined on
defined on  by
by  (the convolution of
(the convolution of  and
and  Then denote by
Then denote by  to be the closure of
to be the closure of  in the weak operator topology in
in the weak operator topology in  It is known that
It is known that  and
and  Furthermore, if
Furthermore, if  is amenable (e.g., when
is amenable (e.g., when  is compact), then
is compact), then

We refer the reader to [43] for more details on these spaces.
Notice that when  is an abelian locally compact group, then
is an abelian locally compact group, then  and
and  where
where  is the dual group of
is the dual group of  It follows from Theorem 4.2 that
It follows from Theorem 4.2 that  was the weak
was the weak -normal structure if and only if
-normal structure if and only if  is discrete, or equivalently,
is discrete, or equivalently,  is compact.
is compact.
Theorem 4.6.
If  is compact, then
is compact, then  has weak
has weak -normal structure and hence the FPP
-normal structure and hence the FPP .
.
For a Banach space (resp., dual Banach space)  we say that
we say that  has the weak-FPP (weak
has the weak-FPP (weak -FPP) for left reversible semigroup if whenever
-FPP) for left reversible semigroup if whenever  is a left reversible semitopological semigroup and
is a left reversible semitopological semigroup and  is a weak (resp., weak
is a weak (resp., weak compact convex subset of
compact convex subset of  and
and  is a separately continuous representation of
is a separately continuous representation of  as nonexpansive mappings from
as nonexpansive mappings from  into
into  then there is a common fixed point in
then there is a common fixed point in  for
for 
Theorem 4.7.
If  is a separable compact group, then
is a separable compact group, then  has the weak
has the weak - FPP for left reversible semigroups.
- FPP for left reversible semigroups.
Open Problem 5.
Can separability be dropped from Theorem 4.7?
A locally compact group  is called an [IN]-group if there is a compact neighbourhood of the identity
is called an [IN]-group if there is a compact neighbourhood of the identity  in
in  which is invariant under the inner automorphisms. The class of [IN]-group contains all discrete groups, abelian groups and compact groups. Every [IN]-group is unimodular.
which is invariant under the inner automorphisms. The class of [IN]-group contains all discrete groups, abelian groups and compact groups. Every [IN]-group is unimodular.
We now investigate the weak fixed point property for a semigroup. A group  is said to an [AU]-group if the von Neumann algebra generated by every continuous unitary representation of
is said to an [AU]-group if the von Neumann algebra generated by every continuous unitary representation of  is atomic (i.e., every nonzero projection in the van Neumann algebra majorizes a nonzero minimal projection). It is an [AR]-group if the von Neumann algebra
is atomic (i.e., every nonzero projection in the van Neumann algebra majorizes a nonzero minimal projection). It is an [AR]-group if the von Neumann algebra  is atomic. Since
is atomic. Since  is the von Neumann algebra generated by the regular representation, it is clear that every [AU]-group is an [AR]-group. It was shown in [44, Lemma
is the von Neumann algebra generated by the regular representation, it is clear that every [AU]-group is an [AR]-group. It was shown in [44, Lemma  ] that if the predual
] that if the predual  of a von Neumann algebra
of a von Neumann algebra  has the Radon-Nikodym property, then
has the Radon-Nikodym property, then  has the weak fixed point property. In fact, since the property UKK is hereditary, the proof there actually showed that
has the weak fixed point property. In fact, since the property UKK is hereditary, the proof there actually showed that  has property UKK and hence has weak normal structure. For the two preduals
has property UKK and hence has weak normal structure. For the two preduals  and
and  we know from [45, Theorems
we know from [45, Theorems  and
and  ] that the class of groups for which
] that the class of groups for which  and
and  have the Radon-Nikodym property is precisely the [AR]-groups and [AU]-groups, respectively. Thus by Lim's result [16, Theorem
have the Radon-Nikodym property is precisely the [AR]-groups and [AU]-groups, respectively. Thus by Lim's result [16, Theorem  ] we have the following proposition
] we have the following proposition
Proposition 4.8.
Let  be a locally compact group.
be a locally compact group.
(a)If  is an [AR]-group, then
is an [AR]-group, then  has the weak fixed point property for left reversible semigroups.
has the weak fixed point property for left reversible semigroups.
(b)If  is an [AU]-group, then
is an [AU]-group, then  has the weak fixed point property for left reversible semigroups.
has the weak fixed point property for left reversible semigroups.
Proposition 4.9.
Let  be an [IN]-group. Then the following are equivalent.
be an [IN]-group. Then the following are equivalent.
(a) is compact.
is compact.
(b) has property UKK.
has property UKK.
(c) has weak normal structure.
has weak normal structure.
(d) has the weak fixed point property for left reversible semigroups.
has the weak fixed point property for left reversible semigroups.
(e) has the weak fixed point property.
has the weak fixed point property.
(f) has the Radon-Nikodym property.
has the Radon-Nikodym property.
(g) has the Krein-Milman property.
has the Krein-Milman property.
A Banach space  is said to have the fixed point property (FPP) if every bounded closed convex subset of
is said to have the fixed point property (FPP) if every bounded closed convex subset of  has the fixed point property for nonexpansive mapping. As well known, every uniformly convex space has the FPP.
has the fixed point property for nonexpansive mapping. As well known, every uniformly convex space has the FPP.
Theorem 4.10.
Let  be a locally compact group. Then
be a locally compact group. Then  has the FPP if and only if
has the FPP if and only if  is finite.
is finite.
Remark 4.11.
-
(a)
Theorems 4.1, 4.2, 4.4, 4.5 and 4.6 are proved by Lau and Mah in [46]; Theorems 4.3, 4.7, and Propositions 4.8 and 4.9 are proved by Lau and Mah in [47] and by Lau and Leinert in [48].
-
(b)
Upon the completion of this paper, the author received a preprint from Professor Narcisse Randrianantoanina [49], where he answered an old question in [50] (see also [23]) and showed that for any Hilbert space
 (separable or not) the trace class opertors on
(separable or not) the trace class opertors on 
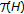 has the weak
has the weak -FPP for left reversible semigroups. He is also able to remove the separability condition in our Theorem 4.7, and show that for anylocally compact group G:
-FPP for left reversible semigroups. He is also able to remove the separability condition in our Theorem 4.7, and show that for anylocally compact group G:
(i) has the weak FPP if and only if is an [AR]-group;
has the weak FPP if and only if is an [AR]-group;
(ii) has the weak-FPP if and only if
has the weak-FPP if and only if  is an [AU]-group. In this case,
is an [AU]-group. In this case,  even has the weak-FPP for left reversible semigroup.
even has the weak-FPP for left reversible semigroup.
We are grateful to Professor Randrianantoanina for sending us a copy of his work.
-
(c)
An example of an [AU]-group
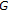 which is not compact is the Fell group which is the semidirect product of the additive
which is not compact is the Fell group which is the semidirect product of the additive  -adic number field
-adic number field 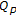 and the multiplicative compact group of
and the multiplicative compact group of  -adic units for a fixed prime
-adic units for a fixed prime 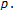 So
So 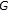 is solvable and hence amenable. We claim that
is solvable and hence amenable. We claim that 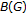 cannot have property KK
cannot have property KK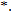 Indeed, the Fell group
Indeed, the Fell group  is separable. Hence
is separable. Hence 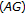 is norm separable (see [29]). So the proof of [51] shows that there is a bounded approximate identity in
is norm separable (see [29]). So the proof of [51] shows that there is a bounded approximate identity in 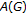 consisting of a sequence
consisting of a sequence 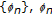 positive definite with norm 1. The sequence
positive definite with norm 1. The sequence 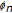 converges to
converges to  in
in 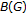 in the weak
in the weak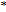 -topology. Now if
-topology. Now if 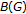 has property KK
has property KK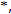 then
then  and so
and so 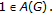 In particular
In particular 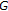 is compact. See [52] for a more general result.
is compact. See [52] for a more general result. -
(d)
Theorem 4.10 is proved by Lau and Leinert in [48]. In a preprint of Hernandez Linares and Japon [53] sent to the author just recently, they have shown that if
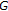 is compact and separable, then
is compact and separable, then  can be renormed to have the FPP. This generalizes an earlier result of Lin [54] who proves that
can be renormed to have the FPP. This generalizes an earlier result of Lin [54] who proves that 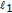 can be renormed to have the FPP. Note that if
can be renormed to have the FPP. Note that if 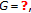 the circle group, then
the circle group, then 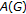 is isometric isomorphic to
is isometric isomorphic to 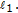 We are grateful to Professor Japon for providing us with a preprint of their work.
We are grateful to Professor Japon for providing us with a preprint of their work. -
(e)
Other related results for this section can also be found in [55].
References
Kirk WA: A fixed point theorem for mappings which do not increase distances. The American Mathematical Monthly 1965, 72: 1004–1006. 10.2307/2313345
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Alspach DE: A fixed point free nonexpansive map. Proceedings of the American Mathematical Society 1981,82(3):423–424. 10.1090/S0002-9939-1981-0612733-0
Berglund JF, Junghenn HD, Milnes P: Analysis on Semigroups, Canadian Mathematical Society Series of Monographs and Advanced Texts. John Wiley & Sons, New York, NY, USA; 1989:xiv+334.
Lau AT-M, Takahashi W: Invariant means and fixed point properties for non-expansive representations of topological semigroups. Topological Methods in Nonlinear Analysis 1995,5(1):39–57.
Day MM: Amenable semigroups. Illinois Journal of Mathematics 1957, 1: 509–544.
Hewitt E: On two problems of Urysohn. Annals of Mathematics 1946, 47: 503–509. 10.2307/1969089
Lau AT-M, Takahashi W: Nonlinear submeans on semigroups. Topological Methods in Nonlinear Analysis 2003,22(2):345–353.
Lau AT-M, Takahashi W: Fixed point and non-linear ergodic theorems for semigroups of nonlinear mappings. In Handbook of Metric Fixed Point Theory. Edited by: Kirk WA, Sims B. Kluwer Academic Publishers, Dordrecht, The Netherlands; 2001:517–555.
DeMarr R: Common fixed points for commuting contraction mappings. Pacific Journal of Mathematics 1963, 13: 1139–1141.
Lau AT-M, Takahashi W: Invariant submeans and semigroups of nonexpansive mappings on Banach spaces with normal structure. Journal of Functional Analysis 1996,142(1):79–88. 10.1006/jfan.1996.0144
Mitchell T: Fixed points of reversible semigroups of nonexpansive mappings. Kōdai Mathematical Seminar Reports 1970, 22: 322–323. 10.2996/kmj/1138846168
Takahashi W: Fixed point theorem for amenable semigroup of nonexpansive mappings. Kōdai Mathematical Seminar Reports 1969, 21: 383–386. 10.2996/kmj/1138845984
Belluce LP, Kirk WA: Nonexpansive mappings and fixed-points in Banach spaces. Illinois Journal of Mathematics 1967, 11: 474–479.
Holmes RD, Lau AT-M: Non-expansive actions of topological semigroups and fixed points. Journal of the London Mathematical Society 1972, 5: 330–336. 10.1112/jlms/s2-5.2.330
Lim TC: Characterizations of normal structure. Proceedings of the American Mathematical Society 1974, 43: 313–319. 10.1090/S0002-9939-1974-0361728-X
Holmes RD, Lau AT-M: Asymptotically non-expansive actions of topological semigroups and fixed points. Bulletin of the London Mathematical Society 1971, 3: 343–347. 10.1112/blms/3.3.343
Bruck RE Jr.: A common fixed point theorem for a commuting family of nonexpansive mappings. Pacific Journal of Mathematics 1974, 53: 59–71.
Belluce LP, Kirk WA: Fixed-point theorems for families of contraction mappings. Pacific Journal of Mathematics 1966, 18: 213–217.
Browder FE: Nonexpansive nonlinear operators in a Banach space. Proceedings of the National Academy of Sciences of the United States of America 1965, 54: 1041–1044. 10.1073/pnas.54.4.1041
Lau AT-M, Nishiura K, Takahashi W: Nonlinear ergodic theorems for semigroups of nonexpansive mappings and left ideals. Nonlinear Analysis: Theory, Methods & Applications 1996,26(8):1411–1427. 10.1016/0362-546X(94)00347-K
Lau AT-M: Invariant means on almost periodic functions and fixed point properties. The Rocky Mountain Journal of Mathematics 1973, 3: 69–76. 10.1216/RMJ-1973-3-1-69
Lau AT-M, Zhang Y: Fixed point properties of semigroups of non-expansive mappings. Journal of Functional Analysis 2008,254(10):2534–2554. 10.1016/j.jfa.2008.02.006
Granirer E, Lau AT-M: Invariant means on locally compact groups. Illinois Journal of Mathematics 1971, 15: 249–257.
Lau AT-M: Amenability of semigroups. In The Analytical and Topological Theory of Semigroups, De Gruyter Expositions in Mathematics. Volume 1. Edited by: Hofmann KH, Lawson JD, Pym JS. de Gruyter, Berlin, Germany; 1990:313–334.
Hsu R: Topics on weakly almost periodic functions, Ph.D. thesis. SUNY at Buffalo, Buffalo, NY, USA; 1985.
Lau AT-M, Takahashi W: Fixed point properties for semigroup of nonexpansive mappings on Fréchet spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(11):3837–3841. 10.1016/j.na.2008.07.041
Bartoszek W: Nonexpansive actions of topological semigroups on strictly convex Banach spaces and fixed points. Proceedings of the American Mathematical Society 1988,104(3):809–811. 10.1090/S0002-9939-1988-0964861-4
Holmes RD, Lau AT-M: Almost fixed points of semigroups of non-expansive mappings. Studia Mathematica 1972, 43: 217–218.
Kang JI: Fixed point set of semigroups of non-expansive mappings and amenability. Journal of Mathematical Analysis and Applications 2008,341(2):1445–1456. 10.1016/j.jmaa.2007.11.050
Kang JI: Fixed points of non-expansive mappings associated with invariant means in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2008,68(11):3316–3324. 10.1016/j.na.2007.03.018
Lau AT-M: Some fixed point theorems and
 -algebras. In Fixed Point Theory and Its Applications. Edited by: Swaminathan S. Academic Press, Orlando, Fla, USA; 1976:121–129.
-algebras. In Fixed Point Theory and Its Applications. Edited by: Swaminathan S. Academic Press, Orlando, Fla, USA; 1976:121–129.Lau AT-M: Semigroup of nonexpansive mappings on a Hilbert space. Journal of Mathematical Analysis and Applications 1985,105(2):514–522. 10.1016/0022-247X(85)90066-6
Lau AT-M, Mah PF: Quasinormal structures for certain spaces of operators on a Hilbert space. Pacific Journal of Mathematics 1986,121(1):109–118.
Lau AT-M, Takahashi W: Invariant means and semigroups of nonexpansive mappings on uniformly convex Banach spaces. Journal of Mathematical Analysis and Applications 1990,153(2):497–505. 10.1016/0022-247X(90)90228-8
Lau AT-M, Wong CS: Common fixed points for semigroups of mappings. Proceedings of the American Mathematical Society 1973, 41: 223–228. 10.1090/S0002-9939-1973-0322837-3
Lim TC: A fixed point theorem for families on nonexpansive mappings. Pacific Journal of Mathematics 1974, 53: 487–493.
Schechtman G: On commuting families of nonexpansive operators. Proceedings of the American Mathematical Society 1982,84(3):373–376. 10.1090/S0002-9939-1982-0640234-3
Lim TC: Asymptotic centers and nonexpansive mappings in conjugate Banach spaces. Pacific Journal of Mathematics 1980,90(1):135–143.
Huff R: Banach spaces which are nearly uniformly convex. The Rocky Mountain Journal of Mathematics 1980,10(4):743–749. 10.1216/RMJ-1980-10-4-743
van Dulst D, Sims B: Fixed points of nonexpansive mappings and Chebyshev centers in Banach spaces with norms of type (KK). In Banach Space Theory and Its Applications (Bucharest, 1981), Lecture Notes in Mathematics. Volume 991. Springer, Berlin, Germany; 1983:35–43. 10.1007/BFb0061556
Lennard C:
 is uniformly Kadec-Klee. Proceedings of the American Mathematical Society 1990,109(1):71–77.
is uniformly Kadec-Klee. Proceedings of the American Mathematical Society 1990,109(1):71–77.Eymard P: L'algèbre de Fourier d'un groupe localement compact. Bulletin de la Société Mathématique de France 1964, 92: 181–236.
Lau AT-M, Mah PF, Ülger A: Fixed point property and normal structure for Banach spaces associated to locally compact groups. Proceedings of the American Mathematical Society 1997,125(7):2021–2027. 10.1090/S0002-9939-97-03773-8
Taylor KF: Geometry of the Fourier algebras and locally compact groups with atomic unitary representations. Mathematische Annalen 1983,262(2):183–190. 10.1007/BF01455310
Lau AT-M, Mah PF: Normal structure in dual Banach spaces associated with a locally compact group. Transactions of the American Mathematical Society 1988,310(1):341–353. 10.1090/S0002-9947-1988-0937247-0
Lau AT-M, Mah PF: Fixed point property for Banach algebras associated to locally compact groups. Journal of Functional Analysis 2010,258(2):357–372. 10.1016/j.jfa.2009.07.011
Lau AT-M, Leinert M: Fixed point property and the Fourier algebra of a locally compact group. Transactions of the American Mathematical Society 2008,360(12):6389–6402. 10.1090/S0002-9947-08-04622-9
Randrianantoanina N: Fixed point properties of semigroups of nonexpansive mappings. Journal of Functional Analysis, (to appear)
Lau AT-M: Fixed point property for reversible semigroup of nonexpansive mappings on
 -compact convex sets. In Fixed Point Theory and Applications. Volume 3. Nova Science Publishers, Huntington, NY, USA; 2002:167–172.
-compact convex sets. In Fixed Point Theory and Applications. Volume 3. Nova Science Publishers, Huntington, NY, USA; 2002:167–172.Lau AT-M: Uniformly continuous functionals on the Fourier algebra of any locally compact group. Transactions of the American Mathematical Society 1979, 251: 39–59.
Bekka MB, Kaniuth E, Lau AT-M, Schlichting G:
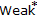 -closedness of subspaces of Fourier-Stieltjes algebras and
-closedness of subspaces of Fourier-Stieltjes algebras and 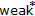 -continuity of the restriction map. Transactions of the American Mathematical Society 1998,350(6):2277–2296. 10.1090/S0002-9947-98-01835-2
-continuity of the restriction map. Transactions of the American Mathematical Society 1998,350(6):2277–2296. 10.1090/S0002-9947-98-01835-2Hernandez Linares CA, Japon MA: A renorming in some Banach spaces with application to fixed point theory. Journal of Functional Analysis, (to appear)
Lin P-K: There is an equivalent norm on
 that has the fixed point property. Nonlinear Analysis: Theory, Methods & Applications 2008,68(8):2303–2308. 10.1016/j.na.2007.01.050
that has the fixed point property. Nonlinear Analysis: Theory, Methods & Applications 2008,68(8):2303–2308. 10.1016/j.na.2007.01.050Lau AT-M, Ülger A: Some geometric properties on the Fourier and Fourier-Stieltjes algebras of locally compact groups, Arens regularity and related problems. Transactions of the American Mathematical Society 1993,337(1):321–359. 10.2307/2154325
Acknowledgment
This research is supported by NSERC Grant A-7679 and is dedicated to Professor William A. Kirk with admiration and respect.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lau, AM. Normal Structure and Common Fixed Point Properties for Semigroups of Nonexpansive Mappings in Banach Spaces. Fixed Point Theory Appl 2010, 580956 (2010). https://doi.org/10.1155/2010/580956
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/580956
 has an identity by considering
has an identity by considering 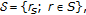 the semigroup of right translations, on the weakly compact convex sets
the semigroup of right translations, on the weakly compact convex sets 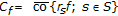 for each
for each 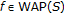 (see [
(see [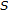 is a discrete semigroup, the following implication diagram is known:
is a discrete semigroup, the following implication diagram is known: 
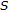 is left reversible
is left reversible  has a
has a  " for any semitopological semigroup was established in [
" for any semitopological semigroup was established in [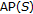 has
has 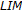 "
"  "
"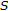 is left reversible" (see [
is left reversible" (see [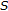 is left reversible
is left reversible  has
has 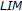 " for discrete semigroups was proved by Hsu [
" for discrete semigroups was proved by Hsu [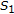 is the bicyclic semigroup generated by
is the bicyclic semigroup generated by  such that
such that  is the unit of
is the unit of 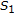 and
and 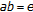 and
and 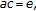 then
then  has a
has a  but
but  is not left reversible. Also if
is not left reversible. Also if 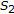 is the bicyclic semigroup generated by
is the bicyclic semigroup generated by  where
where  is the unit element and
is the unit element and 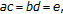 then
then  has a
has a  but
but 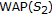 does not have a
does not have a 
 (separable or not) the trace class opertors on
(separable or not) the trace class opertors on 
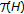 has the weak
has the weak -FPP for left reversible semigroups. He is also able to remove the separability condition in our Theorem 4.7, and show that for anylocally compact group G:
-FPP for left reversible semigroups. He is also able to remove the separability condition in our Theorem 4.7, and show that for anylocally compact group G: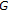 which is not compact is the Fell group which is the semidirect product of the additive
which is not compact is the Fell group which is the semidirect product of the additive  -adic number field
-adic number field 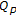 and the multiplicative compact group of
and the multiplicative compact group of  -adic units for a fixed prime
-adic units for a fixed prime 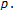 So
So 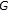 is solvable and hence amenable. We claim that
is solvable and hence amenable. We claim that 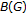 cannot have property KK
cannot have property KK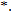 Indeed, the Fell group
Indeed, the Fell group  is separable. Hence
is separable. Hence 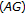 is norm separable (see [
is norm separable (see [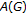 consisting of a sequence
consisting of a sequence 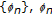 positive definite with norm 1. The sequence
positive definite with norm 1. The sequence 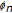 converges to
converges to  in
in 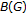 in the weak
in the weak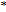 -topology. Now if
-topology. Now if 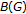 has property KK
has property KK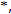 then
then  and so
and so 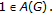 In particular
In particular 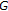 is compact. See [
is compact. See [ is compact and separable, then
is compact and separable, then  can be renormed to have the FPP. This generalizes an earlier result of Lin [
can be renormed to have the FPP. This generalizes an earlier result of Lin [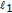 can be renormed to have the FPP. Note that if
can be renormed to have the FPP. Note that if 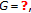 the circle group, then
the circle group, then 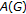 is isometric isomorphic to
is isometric isomorphic to 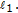 We are grateful to Professor Japon for providing us with a preprint of their work.
We are grateful to Professor Japon for providing us with a preprint of their work. -algebras. In Fixed Point Theory and Its Applications. Edited by: Swaminathan S. Academic Press, Orlando, Fla, USA; 1976:121–129.
-algebras. In Fixed Point Theory and Its Applications. Edited by: Swaminathan S. Academic Press, Orlando, Fla, USA; 1976:121–129. is uniformly Kadec-Klee. Proceedings of the American Mathematical Society 1990,109(1):71–77.
is uniformly Kadec-Klee. Proceedings of the American Mathematical Society 1990,109(1):71–77. -compact convex sets. In Fixed Point Theory and Applications. Volume 3. Nova Science Publishers, Huntington, NY, USA; 2002:167–172.
-compact convex sets. In Fixed Point Theory and Applications. Volume 3. Nova Science Publishers, Huntington, NY, USA; 2002:167–172.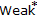 -closedness of subspaces of Fourier-Stieltjes algebras and
-closedness of subspaces of Fourier-Stieltjes algebras and 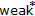 -continuity of the restriction map. Transactions of the American Mathematical Society 1998,350(6):2277–2296. 10.1090/S0002-9947-98-01835-2
-continuity of the restriction map. Transactions of the American Mathematical Society 1998,350(6):2277–2296. 10.1090/S0002-9947-98-01835-2 that has the fixed point property. Nonlinear Analysis: Theory, Methods & Applications 2008,68(8):2303–2308. 10.1016/j.na.2007.01.050
that has the fixed point property. Nonlinear Analysis: Theory, Methods & Applications 2008,68(8):2303–2308. 10.1016/j.na.2007.01.050