- Research Article
- Open access
- Published:
A Common End Point Theorem for Set-Valued Generalized 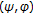 -Weak Contraction
-Weak Contraction
Fixed Point Theory and Applications volume 2010, Article number: 509658 (2010)
Abstract
We introduce the class of generalized  -weak contractive set-valued mappings on a metric space. We establish that such mappings have a unique common end point under certain weak conditions. The theorem obtained generalizes several recent results on single-valued as well as certain set-valued mappings.
-weak contractive set-valued mappings on a metric space. We establish that such mappings have a unique common end point under certain weak conditions. The theorem obtained generalizes several recent results on single-valued as well as certain set-valued mappings.
1. Introduction and Preliminaries
Alber and Guerre-Delabriere [1] defined weakly contractive maps on a Hilbert space and established a fixed point theorem for such a map. Afterwards, Rhoades [2], using the notion of weakly contractive maps, obtained a fixed point theorem in a complete metric space. Dutta and Choudhury [3] generalized the weak contractive condition and proved a fixed point theorem for a selfmap, which in turn generalizes theorem 1 in [2] and the corresponding result in [1]. The study of common fixed points of mappings satisfying certain contractive conditions has been at the center of vigorous research activity. Beg and Abbas [4] obtained a common fixed point theorem extending weak contractive condition for two maps. In this direction, Zhang and Song [5] introduced the concept of a generalized  -weak contraction condition and obtained a common fixed point for two maps, and Ðorić [6] proved a common fixed point theorem for generalized
-weak contraction condition and obtained a common fixed point for two maps, and Ðorić [6] proved a common fixed point theorem for generalized  -weak contractions. On the other hand, there are many theorems in the existing literature which deal with fixed point of multivalued mappings. In some cases, multivalued mapping
-weak contractions. On the other hand, there are many theorems in the existing literature which deal with fixed point of multivalued mappings. In some cases, multivalued mapping  defined on a nonempty set
defined on a nonempty set  assumes a compact value
assumes a compact value  for each
for each  in
in  . There are the situations when, for each
. There are the situations when, for each  in
in  ,
, is assumed to be closed and bounded subset of
is assumed to be closed and bounded subset of  . To prove existence of fixed point of such mappings, it is essential for mappings to satisfy certain contractive conditions which involve Hausdorff metric.
. To prove existence of fixed point of such mappings, it is essential for mappings to satisfy certain contractive conditions which involve Hausdorff metric.
The aim of this paper is to obtain the common end point, a special case of fixed point, of two multivlaued mappings without appeal to continuity of any map involved therein. It is also noted that our results do not require any commutativity condition to prove an existence of common end point of two mappings. These results extend, unify, and improve the earlier comparable results of a number of authors.
Let  be a metric space, and let
be a metric space, and let  be the class of all nonempty bounded subsets of
be the class of all nonempty bounded subsets of  . We define the functions
. We define the functions  and
and  as follows:
as follows:

where  denotes the set of all positive real numbers. For
denotes the set of all positive real numbers. For  and
and  , we write
, we write  and
and  , respectively. Clearly,
, respectively. Clearly,  . We appeal to the fact that
. We appeal to the fact that  if and only if
if and only if  for
for  and
and

for  . A point
. A point  is called a fixed point of
is called a fixed point of  if
if  . If there exists a point
. If there exists a point  such that
such that  , then
, then  is termed as an end point of the mapping
is termed as an end point of the mapping  .
.
2. Main Results
In this section, we established an end point theorem which is a generalization of fixed point theorem for generalized  -weak contractions. The idea is in line with Theorem 2.1 in [6] and theorem 1 in [5].
-weak contractions. The idea is in line with Theorem 2.1 in [6] and theorem 1 in [5].
Definition 2.1.
Two set-valued mappings  are said to satisfy the property of generalized
are said to satisfy the property of generalized -weak contraction if the inequality
-weak contraction if the inequality

where

holds for all  and for given functions
and for given functions  .
.
Theorem 2.2.
Let  be a complete metric space, and let
be a complete metric space, and let  be two set-valued mappings that satisfy the property of generalized
be two set-valued mappings that satisfy the property of generalized  -weak contraction, where
-weak contraction, where
(a) is a continuous monotone nondecreasing function with
is a continuous monotone nondecreasing function with  if and only if
if and only if  ,
,
(b) is a lower semicontinuous function with
is a lower semicontinuous function with  if and only if
if and only if 
then there exists the unique point  such that
such that  .
.
Proof.
We construct the convergent sequence  in
in  and prove that the limit point of that sequence is a unique common fixed point for
and prove that the limit point of that sequence is a unique common fixed point for  and
and  . For a given
. For a given  and nonnegative integer
and nonnegative integer  let
let

and let

The sequences and
and are convergent. Suppose that
are convergent. Suppose that  is an odd number. Substituting
is an odd number. Substituting  and
and  in (2.1) and using properties of functions
in (2.1) and using properties of functions  and
and  , we obtain
, we obtain

which implies that

Now from (2.2) and from triangle inequality for  , we have
, we have

If  , then
, then

From (2.6) and (2.8) it follows that

It furthermore implies that

which is a contradiction. So, we have

Similarly, we can obtain inequalities (2.11) also in the case when  is an even number. Therefore, the sequence
is an even number. Therefore, the sequence  defined in (2.4) is monotone nonincreasing and bounded. Let
defined in (2.4) is monotone nonincreasing and bounded. Let  when
when  . From (2.11), we have
. From (2.11), we have

Letting  in inequality
in inequality

we obtain

which is a contradiction unless  . Hence,
. Hence,

From (2.15) and (2.3), it follows that

The sequence is a Cauchy sequence. First, we prove that for each
is a Cauchy sequence. First, we prove that for each  there exists
there exists  such that
such that

Suppose opposite that (2.17) does not hold then there exists  for which we can find nonnegative integer sequences
for which we can find nonnegative integer sequences  and
and  , such that
, such that  is the smallest element of the sequence
is the smallest element of the sequence  for which
for which

This means that

From (2.19) and triangle inequality for  , we have
, we have

Letting  and using (2.15), we can conclude that
and using (2.15), we can conclude that

Moreover, from

using (2.15) and (2.21), we get

and from

using (2.15) and (2.23), we get

Also, from the definition of  (2.2) and from (2.15), (2.23), and (2.25), we have
(2.2) and from (2.15), (2.23), and (2.25), we have

Putting  ,
,  in (2.1), we have
in (2.1), we have

Letting  and using (2.23), (2.26), we get
and using (2.23), (2.26), we get

which is a contradiction with  .
.
Therefore, conclusion (2.17) is true. From the construction of the sequence  , it follows that the same conclusion holds for
, it follows that the same conclusion holds for  . Thus, for each
. Thus, for each  there exists
there exists  such that
such that

From (2.4) and (2.29), we conclude that  is a Cauchy sequence.
is a Cauchy sequence.
In complete metric space  , there exists
, there exists  such that
such that  as
as  .
.
The point is end point of
is end point of . As the limit point
. As the limit point  is independent of the choice of
is independent of the choice of  , we also get
, we also get

From

we have  as
as  . Since
. Since

letting  and using (2.30), we obtain
and using (2.30), we obtain

which implies  . Hence,
. Hence,  or
or  .
.
The point is also end point for
is also end point for . It is easy to see that
. It is easy to see that  . Using that
. Using that  is fixed point for
is fixed point for  , we have
, we have

and using an argument similar to the above, we conclude that  or
or  .
.
The point is a unique end point for
is a unique end point for and
and . If there exists another fixed point
. If there exists another fixed point  , then
, then  and from
and from

we conclude that  .
.
The proof is completed.
The Theorem 2.2 established that set-valued mappings  and
and  under weak condition (2.1) have the unique common end point
under weak condition (2.1) have the unique common end point  . Now, we give an example to support our result.
. Now, we give an example to support our result.
Example 2.3.
Consider  as a subspace of real line with usual metric,
as a subspace of real line with usual metric,  . Let
. Let  be defined as
be defined as

and take  as
as  and
and .
.
From Tables 1 and 2, it is easy to verify that mappings  and
and  satisfy condition (2.1).
satisfy condition (2.1).
Therefore,  and
and  satisfy the property of generalized
satisfy the property of generalized  . Note that
. Note that  and
and  have unique common end point.
have unique common end point.  . Also, note that for
. Also, note that for  condition (2.1), which became analog to condition (2.1) in [5], does not hold. For example,
condition (2.1), which became analog to condition (2.1) in [5], does not hold. For example,  while
while  .
.
Remark 2.4.
The Theorem 2.2 generalizes recent results on single-valued weak contractions given in [3, 5, 6]. The example above shows that function  in (2.1) gives an improvement over condition (2.1) in [5].
in (2.1) gives an improvement over condition (2.1) in [5].
References
Alber YI, Guerre-Delabriere S: Principle of weakly contractive maps in Hilbert spaces. In New Results, in Operator Theory and Its Applications, Operator Theory: Advances and Applications. Volume 98. Edited by: Gohberg I, Lyubich Y. Birkhäuser, Basel, Switzerland; 1997:7–22.
Rhoades BE: Some theorems on weakly contractive maps. Nonlinear Analysis: Theory, Methods & Applications 2001,47(4):2683–2693. 10.1016/S0362-546X(01)00388-1
Dutta PN, Choudhury BS: A generalisation of contraction principle in metric spaces. Fixed Point Theory and Applications 2008, 2008:- 8.
Beg I, Abbas M: Coincidence point and invariant approximation for mappings satisfying generalized weak contractive condition. Fixed Point Theory and Applications 2006, 2006:-7.
Zhang Q, Song Y: Fixed point theory for generalized
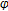 -weak contractions. Applied Mathematics Letters 2009,22(1):75–78. 10.1016/j.aml.2008.02.007
-weak contractions. Applied Mathematics Letters 2009,22(1):75–78. 10.1016/j.aml.2008.02.007Ðorić D: Common fixed point for generalized
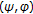 -weak contractions. Applied Mathematics Letters 2009,22(12):1896–1900. 10.1016/j.aml.2009.08.001
-weak contractions. Applied Mathematics Letters 2009,22(12):1896–1900. 10.1016/j.aml.2009.08.001
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abbas, M., Ðorić, D. A Common End Point Theorem for Set-Valued Generalized 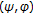 -Weak Contraction.
Fixed Point Theory Appl 2010, 509658 (2010). https://doi.org/10.1155/2010/509658
-Weak Contraction.
Fixed Point Theory Appl 2010, 509658 (2010). https://doi.org/10.1155/2010/509658
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/509658
 -weak contractions. Applied Mathematics Letters 2009,22(1):75–78. 10.1016/j.aml.2008.02.007
-weak contractions. Applied Mathematics Letters 2009,22(1):75–78. 10.1016/j.aml.2008.02.007 -weak contractions. Applied Mathematics Letters 2009,22(12):1896–1900. 10.1016/j.aml.2009.08.001
-weak contractions. Applied Mathematics Letters 2009,22(12):1896–1900. 10.1016/j.aml.2009.08.001