- Research Article
- Open access
- Published:
Approximation of Common Fixed Points of a Countable Family of Relatively Nonexpansive Mappings
Fixed Point Theory and Applications volume 2010, Article number: 407651 (2009)
Abstract
We introduce two general iterative schemes for finding a common fixed point of a countable family of relatively nonexpansive mappings in a Banach space. Under suitable setting, we not only obtain several convergence theorems announced by many authors but also prove them under weaker assumptions. Applications to the problem of finding a common element of the fixed point set of a relatively nonexpansive mapping and the solution set of an equilibrium problem are also discussed.
1. Introduction and Preliminaries
Let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  , and let
, and let  be a mapping from
be a mapping from  into itself. When
into itself. When  is a sequence in
is a sequence in  , we denote strong convergence of
, we denote strong convergence of  to
to  by
by  and weak convergence by
and weak convergence by  . We also denote the weak
. We also denote the weak convergence of a sequence
convergence of a sequence  to
to  in the dual
in the dual  by
by  . A point
. A point  is an asymptotic fixed point of
is an asymptotic fixed point of  if there exists
if there exists  in
in  such that
such that  and
and  . We denote
. We denote  and
and  by the set of fixed points and of asymptotic fixed points of
by the set of fixed points and of asymptotic fixed points of  , respectively. A Banach space
, respectively. A Banach space  is said to be strictly convex if
is said to be strictly convex if  for
for  and
and  . It is also said to be uniformly convex if for each
. It is also said to be uniformly convex if for each  , there exists
, there exists  such that
such that  for
for  and
and  . The space
. The space  is said to be smooth if the limit
is said to be smooth if the limit

exists for all  . It is also said to be uniformly smooth if the limit exists uniformly in
. It is also said to be uniformly smooth if the limit exists uniformly in  .
.
Many problems in nonlinear analysis can be formulated as a problem of finding a fixed point of a certain mapping or a common fixed point of a family of mappings. This paper deals with a class of nonlinear mappings, so-called relatively nonexpansive mappings introduced by Matsushita and Takahashi [1]. This type of mappings is closely related to the resolvent of maximal monotone operators (see [2–4]).
Let  be a smooth, strictly convex and reflexive Banach space and let
be a smooth, strictly convex and reflexive Banach space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Throughout this paper, we denote by
. Throughout this paper, we denote by  the function defined by
the function defined by

where  is the normalized duality mapping from
is the normalized duality mapping from  to the dual space
to the dual space  given by the following relation:
given by the following relation:

We know that if  is smooth, strictly convex, and reflexive, then the duality mapping
is smooth, strictly convex, and reflexive, then the duality mapping  is single-valued, one-to-one, and onto. The duality mapping
is single-valued, one-to-one, and onto. The duality mapping  is said to be weakly sequentially continuous if
is said to be weakly sequentially continuous if  implies that
implies that  (see [5] for more details).
(see [5] for more details).
Following Matsushita and Takahashi [6], a mapping  is said to be relatively nonexpansive if the following conditions are satisfied:
is said to be relatively nonexpansive if the following conditions are satisfied:
(R1) is nonempty;
is nonempty;
(R2) for all
for all  ,
,  ;
;
(R3) .
.
If  satisfies (R1) and (R2), then
satisfies (R1) and (R2), then  is called relatively quasi-nonexpansive [7]. Obviously, relative nonexpansiveness implies relative quasi-nonexpansiveness but the converse is not true. Relatively quasi-nonexpansive mappings are sometimes called hemirelatively nonexpansive mappings. But we do prefer the former name because in a Hilbert space setting, relatively quasi-nonexpansive mappings are nothing but quasi-nonexpansive.
is called relatively quasi-nonexpansive [7]. Obviously, relative nonexpansiveness implies relative quasi-nonexpansiveness but the converse is not true. Relatively quasi-nonexpansive mappings are sometimes called hemirelatively nonexpansive mappings. But we do prefer the former name because in a Hilbert space setting, relatively quasi-nonexpansive mappings are nothing but quasi-nonexpansive.
In [2], Alber introduced the generalized projection  from
from  onto
onto  as follows:
as follows:

If  is a Hilbert space, then
is a Hilbert space, then  and
and  becomes the metric projection of
becomes the metric projection of  onto
onto  . Alber's generalized projection is an example of relatively nonexpansive mappings. For more example, see [1, 8].
. Alber's generalized projection is an example of relatively nonexpansive mappings. For more example, see [1, 8].
In 2004, Masushita and Takahashi [1, 6] also proved weak and strong convergence theorems for finding a fixed point of a single relatively nonexpansive mapping. Several iterative methods, as a generalization of [1, 6], for finding a common fixed point of the family of relatively nonexpansive mappings have been further studied in [7, 9–14].
Recently, a problem of finding a common element of the set of solutions of an equilibrium problem and the set of fixed points of a relatively nonexpansive mapping is studied by Takahashi and Zembayashi in [15, 16]. The purpose of this paper is to introduce a new iterative scheme which unifies several ones studied by many authors and to deduce the corresponding convergence theorems under the weaker assumptions. More precisely, many restrictions as were the case in other papers are dropped away.
First, we start with some preliminaries which will be used throughout the paper.
Lemma 1.1 (see [7, Lemma  ]).
]).
Let  be a nonempty closed convex subset of a strictly convex and smooth Banach space
be a nonempty closed convex subset of a strictly convex and smooth Banach space  and let
and let  be a relatively quasi-nonexpansive mapping from
be a relatively quasi-nonexpansive mapping from  into itself. Then
into itself. Then  is closed and convex.
is closed and convex.
Lemma 1.2 (see [17, Proposition  ]).
]).
Let  be a nonempty closed convex subset of a smooth, strictly convex, and reflexive Banach space
be a nonempty closed convex subset of a smooth, strictly convex, and reflexive Banach space  . Then
. Then

for all  and
and  .
.
Lemma 1.3 (see [17]).
Let  be a smooth and uniformly convex Banach space and let
be a smooth and uniformly convex Banach space and let  . Then there exists a strictly increasing, continuous, and convex function
. Then there exists a strictly increasing, continuous, and convex function  such that
such that  and
and

for all  .
.
Lemma 1.4 (see [17, Proposition  ]).
]).
Let  be a smooth and uniformly convex Banach space and let
be a smooth and uniformly convex Banach space and let  and
and  be sequences of
be sequences of  such that either
such that either  or
or  is bounded. If
is bounded. If  , then
, then  .
.
Lemma 1.5 (see [2]).
Let  be a nonempty closed convex subset of a smooth, strictly convex, and reflexive Banach space
be a nonempty closed convex subset of a smooth, strictly convex, and reflexive Banach space  , let
, let  and let
and let  . Then
. Then

Lemma 1.6 (see [18]).
Let  be a uniformly convex Banach space and let
be a uniformly convex Banach space and let  . Then there exists a strictly increasing, continuous, and convex function
. Then there exists a strictly increasing, continuous, and convex function  such that
such that  and
and

for all  and
and  .
.
We next prove the following three lemmas which are very useful for our main results.
Lemma 1.7.
Let Let  be a closed convex subset of a smooth Banach space
be a closed convex subset of a smooth Banach space  . Let
. Let  be a relatively quasi-nonexpansive mapping from
be a relatively quasi-nonexpansive mapping from  into
into  and let
and let  be a family of relatively quasi-nonexpansive mappings from
be a family of relatively quasi-nonexpansive mappings from  into itself such that
into itself such that  . The mapping
. The mapping  is defined by
is defined by

for all  and
and  ,
,  such that
such that  . If
. If  and
and  , then
, then

Proof.
The proof of this lemma can be extracted from that of Lemma 1.8; so it is omitted.
If  has a stronger assumption, we have the following lemma.
has a stronger assumption, we have the following lemma.
Lemma 1.8.
Let  be a closed convex subset of a uniformly smooth Banach space
be a closed convex subset of a uniformly smooth Banach space  . Let
. Let  . Then, there exists a strictly increasing, continuous, and convex function
. Then, there exists a strictly increasing, continuous, and convex function  such that
such that  and for each relatively quasi-nonexpansive mapping
and for each relatively quasi-nonexpansive mapping  and each finite family of relatively quasi-nonexpansive mappings
and each finite family of relatively quasi-nonexpansive mappings  such that
such that  ,
,

for all  and
and  , where
, where

 and
and  ,
, such that
such that  .
.
Proof.
Let  . From Lemma 1.6 and
. From Lemma 1.6 and  is uniformly convex, then there exists a strictly increasing, continuous, and convex function
is uniformly convex, then there exists a strictly increasing, continuous, and convex function  such that
such that  and
and

for all  and
and  . Let
. Let  and
and  be relatively quasi-nonexpansive for all
be relatively quasi-nonexpansive for all  such that
such that  . For
. For  and
and  . It follows that
. It follows that

and hence  . Consequently, for
. Consequently, for  ,
,

Then

Thus

Lemma 1.9.
Let  be a closed convex subset of a uniformly smooth and strictly convex Banach space
be a closed convex subset of a uniformly smooth and strictly convex Banach space  . Let
. Let  be a relatively quasi-nonexpansive mapping from
be a relatively quasi-nonexpansive mapping from  into
into  and let
and let  be a family of relatively quasi-nonexpansive mappings from
be a family of relatively quasi-nonexpansive mappings from  into itself such that
into itself such that  . The mapping
. The mapping  is defined by
is defined by

for all  and
and  ,
, such that
such that  . Then, the following hold:
. Then, the following hold:
(1) ,
,
(2) is relatively quasi-nonexpansive.
is relatively quasi-nonexpansive.
Proof.
( ) Clearly,
) Clearly,  . We want to show the reverse inclusion. Let
. We want to show the reverse inclusion. Let  and
and  . Choose
. Choose

From Lemma 1.8, we have

From  for all
for all  and by the properties of
and by the properties of  , we have
, we have

for all  . From
. From  is one to one, we have
is one to one, we have

for all  . Consider
. Consider

Thus  .
.
-
(2)
It follows directly from the above discussion.
2. Weak Convergence Theorem
Theorem 2.1.
Let  be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space
be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space  . Let
. Let  be a family of relatively quasi-nonexpansive mappings and let
be a family of relatively quasi-nonexpansive mappings and let  be a family of relatively quasi-nonexpansive mappings such that
be a family of relatively quasi-nonexpansive mappings such that  . Let the sequence
. Let the sequence  be generated by
be generated by  ,
,

for any  ,
,  for all
for all  ,
,  such that
such that  for all
for all  . Then
. Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection of
is the generalized projection of  onto
onto  .
.
Proof.
Let  . Put
. Put

From Lemma 1.7, we have

Therefore  exists. This implies that
exists. This implies that  and
and  are bounded for all
are bounded for all  .
.
Let  . From (2.3) and
. From (2.3) and  , we have
, we have

Consequently,

In particular,

This implies that  exists. This together with the boundedness of
exists. This together with the boundedness of  gives
gives  . Using Lemma 1.3, there exists a strictly increasing, continuous, and convex function
. Using Lemma 1.3, there exists a strictly increasing, continuous, and convex function  such that
such that  and
and

Since  is a convergent sequence, it follows from the properties of
is a convergent sequence, it follows from the properties of  that
that  is a Cauchy sequence. Since
is a Cauchy sequence. Since  is closed, there exists
is closed, there exists  such that
such that  .
.
We first establish weak convergence theorem for finding a common fixed point of a countable family of relatively quasi-nonexpansive mappings. Recall that, for a family of mappings  with
with  , we say that
, we say that  satisfies the NST-condition [19] if for each bounded sequence
satisfies the NST-condition [19] if for each bounded sequence  in
in  ,
,

where  denotes the set of all weak subsequential limits of a sequence
denotes the set of all weak subsequential limits of a sequence  .
.
Theorem 2.2.
Let  be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space
be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space  . Let
. Let  be a family of relatively quasi-nonexpansive mappings satisfying NST-condition and let
be a family of relatively quasi-nonexpansive mappings satisfying NST-condition and let  be a family of relatively nonexpansive mappings such that
be a family of relatively nonexpansive mappings such that  and suppose that
and suppose that

for all  ,
,  and
and  . Let the sequence
. Let the sequence  be generated by
be generated by  ,
,

for any  ,
,  for all
for all  ,
,  such that
such that  for all
for all  ,
,  for all
for all  . If
. If  is weakly sequentially continuous, then
is weakly sequentially continuous, then  converges weakly to
converges weakly to  , where
, where  .
.
Proof.
Let  . From Theorem 2.1,
. From Theorem 2.1,  exists and hence
exists and hence  and
and  are bounded for all
are bounded for all  . Let
. Let

By Lemma 1.8, there exists a strictly increasing, continuous, and convex function  such that
such that  and
and

In particular, for all  ,
,

Hence,

for all  . Since
. Since  for all
for all  and the properties of
and the properties of  , we have
, we have

for all  . Since
. Since  is uniformly norm-to-norm continuous on bounded sets, we have
is uniformly norm-to-norm continuous on bounded sets, we have

for all  . Since
. Since  is bounded, there exists a subsequence
is bounded, there exists a subsequence  of
of  such that
such that  . Since
. Since  is relatively nonexpansive,
is relatively nonexpansive,  for all
for all  .
.
We show that  . Let
. Let

We note from (2.15) that

Since  is uniformly norm-to-norm continuous on bounded sets, it follows that
is uniformly norm-to-norm continuous on bounded sets, it follows that

Moreover, by (2.9) and the existence of  , we have
, we have

It follows from Lemma 1.4 that  . From (2.19) and
. From (2.19) and  , we have
, we have  . Since
. Since  satisfies NST-condition, we have
satisfies NST-condition, we have  . Hence
. Hence  .
.
Let  . From Lemma 1.5 and
. From Lemma 1.5 and  , we have
, we have

From Theorem 2.1, we know that  . Since
. Since  is weakly sequentially continuous, we have
is weakly sequentially continuous, we have

Moreover, since  is monotone,
is monotone,

Then

Since  is strictly convex,
is strictly convex,  . This implies that
. This implies that  and hence
and hence  .
.
We next apply our result for finding a common element of a fixed point set of a relatively nonexpansive mapping and the solution set of an equilibrium problem. This problem is extensively studied in [11, 14–16]. Let  be a subset of a Banach space
be a subset of a Banach space  and let
and let  be a bifunction. The equilibrium problem for a bifunction
be a bifunction. The equilibrium problem for a bifunction  is to find
is to find  such that
such that  for all
for all  . The set of solutions above is denoted by
. The set of solutions above is denoted by  , that is
, that is

To solve the equilibrium problem, we usually assume that a bifunction  satisfies the following conditions (
satisfies the following conditions ( is closed and convex):
is closed and convex):
(A1) for all
for all  ;
;
(A2) is monotone, that is,
is monotone, that is,  ;
;
(A3)for all  ,
,  ;
;
(A4)for all  ,
,  is convex and lower semicontinuous.
is convex and lower semicontinuous.
The following lemma gives a characterization of a solution of an equilibrium problem.
Lemma 2.3.
Let  be a nonempty closed convex subset of a Banach space
be a nonempty closed convex subset of a Banach space  . Let
. Let  be a bifunction from
be a bifunction from  satisfying (A1)–(A4). Suppose that
satisfying (A1)–(A4). Suppose that  . Then
. Then  if and only if
if and only if  for all
for all  .
.
Proof.
Let  , then
, then  for all
for all  . From (A2), we get that
. From (A2), we get that  for all
for all  .
.
Conversely, assume that  for all
for all  . For any
. For any  , let
, let

Then  and hence
and hence

So  for all
for all  . From (A3), we have
. From (A3), we have

Hence  .
.
Takahashi and Zembayashi proved the following important result.
Lemma 2.4 (see [15, Lemma  ]).
]).
Let  be a nonempty closed convex subset of a uniformly smooth, strictly convex and reflexive Banach space
be a nonempty closed convex subset of a uniformly smooth, strictly convex and reflexive Banach space  . Let
. Let  be a bifunction from
be a bifunction from  satisfying (A1)–(A4). For
satisfying (A1)–(A4). For  and
and  , define a mapping
, define a mapping  as follows:
as follows:

for all  . Then, the following hold:
. Then, the following hold:
(1) is single-valued;
is single-valued;
(2) is a firmly nonexpansive-type mapping [20], that is, for all
is a firmly nonexpansive-type mapping [20], that is, for all 

(3) ;
;
(4) is closed and convex.
is closed and convex.
We now deduce Takahashi and Zembayashi's recent result from Theorem 2.2.
Corollary 2.5 (see [15, Theorem  ]).
]).
Let  be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space
be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4) and let
satisfying (A1)–(A4) and let  be a relatively nonexpansive mapping from
be a relatively nonexpansive mapping from  into itself such that
into itself such that  . Let the sequence
. Let the sequence  be generated by
be generated by  ,
,

for every  ,
,  satisfying
satisfying  and
and  for some
for some  . If
. If  is weakly sequentially continuous, then
is weakly sequentially continuous, then  converges weakly to
converges weakly to  , where
, where  .
.
Proof.
Put  where
where  is defined by Lemma 2.4. Then
is defined by Lemma 2.4. Then  . By reindexing the sequences
. By reindexing the sequences  and
and  of this iteration, we can apply Theorem 2.2 by showing that the family
of this iteration, we can apply Theorem 2.2 by showing that the family  satisfies the condition (2.9) and NST-condition. It is proved in [15, Lemma
satisfies the condition (2.9) and NST-condition. It is proved in [15, Lemma  ] that
] that

To see that  satisfies NST-condition, let
satisfies NST-condition, let  be a bounded sequence in
be a bounded sequence in  such that
such that  and
and  . Suppose that there exists a subsequence
. Suppose that there exists a subsequence  of
of  such that
such that  . Then
. Then  . Since
. Since  is uniformly continuous on bounded sets and
is uniformly continuous on bounded sets and  , we have
, we have

From the definition of  , we have
, we have

Since

and  is lower semicontinuous and convex in the second variable, we have
is lower semicontinuous and convex in the second variable, we have

Thus  for all
for all  . From Lemma 2.3, we have
. From Lemma 2.3, we have  . Then
. Then  satisfies the NST-condition. From Theorem 2.2 where
satisfies the NST-condition. From Theorem 2.2 where  ,
,  converges weakly to
converges weakly to  , where
, where  .
.
Using the same proof as above, we have the following result.
Corollary 2.6 (see [11, Theorem  ]).
]).
Let  be a nonempty and closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty and closed convex subset of a uniformly convex and uniformly smooth Banach space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfies (A1)–(A4) and let
satisfies (A1)–(A4) and let  be two relatively nonexpansive mappings such that
be two relatively nonexpansive mappings such that  . Let the sequence
. Let the sequence  be generated by the following manner:
be generated by the following manner:

Assume that  ,
,  and
and  are three sequences in
are three sequences in  satisfying the following restrictions:
satisfying the following restrictions:
(a) ;
;
(b) ,
,  ;
;
(c) for some
for some  .
.
If  is weakly sequentially continuous, then
is weakly sequentially continuous, then  converges weakly to
converges weakly to  , where
, where  .
.
The following result also follows from Theorem 2.2.
Corollary 2.7 (see [9, Theorem  ]).
]).
Let  be a uniformly smooth and uniformly convex Banach space and let
be a uniformly smooth and uniformly convex Banach space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  be a finite family of relatively nonexpansive mappings from
be a finite family of relatively nonexpansive mappings from  into itself such that
into itself such that  is a nonempty and let
is a nonempty and let  and
and  be sequences such that
be sequences such that  and
and  for all
for all  and
and  for all
for all  . Let
. Let  be a sequence of mappings defined by
be a sequence of mappings defined by

for all  and let the sequence
and let the sequence  be generated by
be generated by  and
and

Then the following hold:
(1)the sequence  is bounded and each weak subsequential limit of
is bounded and each weak subsequential limit of  belongs to
belongs to  ;
;
(2)if the duality mapping  from
from  into
into  is weakly sequentially continuous, then
is weakly sequentially continuous, then  converges weakly to the strong limit of
converges weakly to the strong limit of  .
.
Proof.
Since  is relatively nonexpansive, the family
is relatively nonexpansive, the family  satisfies the NST-condition. Moreover,
satisfies the NST-condition. Moreover,  and
and

Thus the conclusions of this corollary follow.
3. Strong Convergence Theorem
In this section, we prove strong convergence of an iterative sequence generated by the hybrid method in mathematical programming. We start with the following useful common tools.
Lemma 3.1.
Let  be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space
be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space  . Let
. Let  and
and  be families of relatively quasi-nonexpansive mappings such that
be families of relatively quasi-nonexpansive mappings such that  , and
, and

for all  ,
,  and
and  . Let
. Let  be such that
be such that  and
and  are bounded for all
are bounded for all  , and
, and

where  for all
for all  and
and  satisfy
satisfy  for all
for all  ,
,  for all
for all  and
and  . Then the following statements hold:
. Then the following statements hold:
(1) for all
for all  ,
,
(2) ,
,
(3) ,
,
(4)if  , then
, then  for all
for all  ,
,
(5)if  , then
, then  and
and  .
.
Proof.
( ) Since
) Since  and
and  is uniformly norm-to-norm continuous on bounded sets,
is uniformly norm-to-norm continuous on bounded sets,

We note here that  is also bounded. For any
is also bounded. For any  , we have
, we have

( ) Let
) Let  . Using (3.1) and the relative quasi-nonexpansiveness of each
. Using (3.1) and the relative quasi-nonexpansiveness of each  , we have
, we have

By Lemma 1.4 and the boundedness of  , we have
, we have

( ) Since
) Since

we have  .
.
( ) Assume that
) Assume that  . From
. From  , we get that
, we get that  . Since
. Since  is uniformly norm-to-norm continuous on bounded sets, we have
is uniformly norm-to-norm continuous on bounded sets, we have

So,

From (3.8), we have

It follows from  for all
for all  that
that

for all  . Since
. Since  is uniformly norm-to-norm continuous on bounded sets and
is uniformly norm-to-norm continuous on bounded sets and  , we have
, we have

for all  , as desired.
, as desired.
( ) Assume that
) Assume that  . From the assumption and (
. From the assumption and ( ), we have
), we have

Hence  and
and  .
.
Lemma 3.2 (see [21, Lemma  ]).
]).
Let  be a closed convex subset of a strictly convex, smooth and reflexive Banach space
be a closed convex subset of a strictly convex, smooth and reflexive Banach space  satisfying Kadec-Klee property. Let
satisfying Kadec-Klee property. Let  and
and  be a sequence in
be a sequence in  such that
such that  and
and  for all
for all  . Then
. Then  .
.
Recall that a Banach space  satisfies Kadec–Klee property if whenever
satisfies Kadec–Klee property if whenever  is a sequence in
is a sequence in  with
with  and
and  , it follows that
, it follows that  .
.
3.1. The CQ-Method
Theorem 3.3.
Let  be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space
be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space  . Let
. Let  be a family of relatively quasi-nonexpansive mappings satisfying NST-condition and let
be a family of relatively quasi-nonexpansive mappings satisfying NST-condition and let  be a family of relatively nonexpansive mappings such that
be a family of relatively nonexpansive mappings such that  , and
, and

for all  ,
,  and
and  . Let the sequence
. Let the sequence  be generated by
be generated by

for every  ,
,  for all
for all  and
and  satisfying
satisfying  for all
for all  ,
,  for all
for all  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
The proof is broken into 4 steps.
Step 1 ( is well defined).
is well defined).
First, we show that  is closed and convex. Clearly,
is closed and convex. Clearly,  is closed and convex. Since
is closed and convex. Since

then  is closed and convex. Thus
is closed and convex. Thus  is closed and convex.
is closed and convex.
We next show that  . Let
. Let  . Then, from Lemma 1.7,
. Then, from Lemma 1.7,

Thus  . Hence
. Hence  for all
for all  .
.
Next, we show by induction that  for all
for all  . Since
. Since  , we have
, we have

Suppose that  for some
for some  . From
. From  and the definition of the generalized projection, we have
and the definition of the generalized projection, we have

for all  . From
. From  ,
,

for all  . Hence
. Hence  , and we also have
, and we also have  . So, we have
. So, we have  for all
for all  and hence the sequence
and hence the sequence  is well defined.
is well defined.
Step 2 ( ).
).
From the definition of  , we have
, we have  . Using Lemma 1.2, we get
. Using Lemma 1.2, we get

for all  . In particular, since
. In particular, since  and
and  ,
,


for all  . This implies that
. This implies that  exists and
exists and  is bounded. Moreover, from (3.21) and
is bounded. Moreover, from (3.21) and  ,
,

Hence

It follows from  that
that

From (3.25), (3.26), and Lemma 1.4, we have

So  . Using Lemma 3.1(4), we get that
. Using Lemma 3.1(4), we get that

for all  . Since each
. Since each  is relatively nonexpansive,
is relatively nonexpansive,

Step 3 ( ).
).
Let  . From Lemma 3.1(2), we have
. From Lemma 3.1(2), we have

and  . It follows from NST-condition that
. It follows from NST-condition that  .
.
Step 4 ( ).
).
From Steps 2 and 3, we have  . The conclusion follows by Lemma 3.2 and (3.23).
. The conclusion follows by Lemma 3.2 and (3.23).
We apply Theorem 3.3 and the proof of Corollary 2.5 and then obtain the following result.
Corollary 3.4.
Let  ,
,  ,
,  ,
,  be as in Corollary 2.5. Let the sequence
be as in Corollary 2.5. Let the sequence  be generated by
be generated by

for every  ,
,  satisfying
satisfying  and
and  for some
for some  . Then,
. Then,  converges strongly to
converges strongly to  , where
, where  is the generalized projection of
is the generalized projection of  onto
onto  .
.
Remark 3.5.
Corollary 3.4 improves the restriction on  of [15, Theorem
of [15, Theorem  ]. In fact, it is assumed in [15, Theorem
]. In fact, it is assumed in [15, Theorem  ] that
] that  .
.
3.2. The Monotone CQ-Method
Let  be a closed subset of a Banach space
be a closed subset of a Banach space  . Recall that a mapping
. Recall that a mapping  is closed if for each
is closed if for each  in
in  , if
, if  and
and  , then
, then  . A family of mappings
. A family of mappings  with
with  is said to satisfy the
is said to satisfy the  -condition if for each bounded sequence
-condition if for each bounded sequence  in
in  ,
,

Remark 3.6.
-
(1)
If
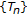 satisfies NST-condition, then
satisfies NST-condition, then  satisfies
satisfies 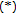 -condition.
-condition. -
(2)
If
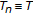 and
and  is closed, then
is closed, then  satisfies
satisfies  -condition.
-condition.
Theorem 3.7.
Let  be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space
be a nonempty closed convex subset of a uniformly smooth and uniformly convex Banach space . Let
. Let  be a family of relatively quasi-nonexpansive mappings satisfying
be a family of relatively quasi-nonexpansive mappings satisfying  -condition and let
-condition and let  be a family of closed relatively quasi-nonexpansive mappings such that
be a family of closed relatively quasi-nonexpansive mappings such that  , and
, and

for all  ,
,  and
and  . Let the sequence
. Let the sequence  be generated by
be generated by

for every  ,
,  satisfying
satisfying  and
and  for all
for all  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
Step 1 ( is well defined).
is well defined).
This step is almost the same as Step 1 of the proof of Theorem 3.3, so it is omitted.
Step 2 ( is a Cauchy sequence in
is a Cauchy sequence in  ).
).
We can follow the proof of Theorem 3.3 and conclude that

exists. Moreover, as  for all
for all  and
and  ,
,

Since  is bounded, it follows from Lemma 1.3 that there exists a strictly increasing, continuous, and convex function
is bounded, it follows from Lemma 1.3 that there exists a strictly increasing, continuous, and convex function  such that
such that  and
and

Since  exists, we have that
exists, we have that  is a Cauchy sequence. Therefore,
is a Cauchy sequence. Therefore,  for some
for some  .
.
Step 3 ( ).
).
Since  , we have
, we have

By Lemma 1.4 and the boundedness of  , we have
, we have

So, we have  . Using Lemma 3.1(4), we get that
. Using Lemma 3.1(4), we get that

for all  . Since each
. Since each  is closed,
is closed,  .
.
Step 4 ( ).
).
Let  . From Lemma 3.1(2), we have
. From Lemma 3.1(2), we have  and
and  . It follows from
. It follows from  -condition that
-condition that  .
.
Step 5 ( ).
).
From Steps 3 and 4, we have  . The conclusion follows by Lemma 3.2 and (3.23).
. The conclusion follows by Lemma 3.2 and (3.23).
Letting  identity and
identity and  yield the following result.
yield the following result.
Corollary 3.8 (see [12, Theorem  ]).
]).
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth real Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth real Banach space  . Let
. Let  be a closed relatively quasi-nonexpansive mapping such that
be a closed relatively quasi-nonexpansive mapping such that  . Assume that
. Assume that  is a sequence in
is a sequence in  such that
such that  . Define a sequence
. Define a sequence  in
in  by the following algorithm:
by the following algorithm:

Then  converges strongly to
converges strongly to  .
.
Letting  identity and
identity and  yield the following result.
yield the following result.
Corollary 3.9 (see [13, Theorem  ]).
]).
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth real Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth real Banach space  . Let
. Let  be two closed relatively quasi-nonexpansive mappings from
be two closed relatively quasi-nonexpansive mappings from  into itself such that
into itself such that  . Define a sequence
. Define a sequence  in
in  be the following algorithm:
be the following algorithm:

with the conditions:  with
with  and
and
(1) ;
;
(2) ;
;
(3) for some
for some  .
.
Then  converges strongly to
converges strongly to  .
.
Remark 3.10.
Using Theorem 3.7, we can show that the conclusion of Corollary 3.9 remains true under the more general restrictions on  and
and  :
:
(1) are arbitrary;
are arbitrary;
(2) and
and  .
.
3.3. The Shrinking Projection Method
Theorem 3.11.
Let  be as in Theorem 3.7. Let the sequence
be as in Theorem 3.7. Let the sequence  be generated by
be generated by

for every  ,
,  for all
for all  and
and  satisfies
satisfies  for all
for all  ,
,  for all
for all  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
The proof is almost the same as the proofs of Theorems 3.3 and 3.7; so it is omitted.
In particular, applying Theorem 3.11 gives the following result.
Corollary 3.12.
Let  be as in Corollary 2.5. Let the sequence
be as in Corollary 2.5. Let the sequence  be generated by
be generated by  ,
,  and
and

for every  , where
, where  is the duality mapping on
is the duality mapping on  . Assume that
. Assume that  satisfies
satisfies  and
and  for some
for some  . Then
. Then  converges strongly to
converges strongly to  , where
, where  is the generalized projection of
is the generalized projection of  onto
onto  .
.
Remark 3.13.
Corollary 3.12 improves the restriction on  of [16, Theorem
of [16, Theorem  ]. In fact, it is assumed in [16, Theorem
]. In fact, it is assumed in [16, Theorem  ] that
] that  .
.
Corollary 3.14 (see [11, Theorem  ]).
]).
Let  be a nonempty and closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty and closed convex subset of a uniformly convex and uniformly smooth Banach space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4) and let
satisfying (A1)–(A4) and let  be two closed relatively quasi-nonexpansive mappings such that
be two closed relatively quasi-nonexpansive mappings such that  . Let the sequence
. Let the sequence  be generated by the following manner:
be generated by the following manner:

Assume that  ,
,  and
and  are three sequences in
are three sequences in  satisfying the restrictions:
satisfying the restrictions:
(a) ;
;
(b) ,
,  ;
;
(c) for some
for some  .
.
Then  converges strongly to
converges strongly to  .
.
Remark 3.15.
The conclusion of Corollary 3.14 remains true under the more general assumption; that is, we can replace (b) by the following one:
(b′) and
and  .
.
We also deduce the following result.
Corollary 3.16 (see [14, Theorem  ]).
]).
Let  be as in Corollary 3.14. Let the sequences
be as in Corollary 3.14. Let the sequences  ,
,  and
and  be generated by the following:
be generated by the following:

Assume that  ,
,  and
and  are three sequences in
are three sequences in  satisfying the following restrictions:
satisfying the following restrictions:
(a) ;
;
(b) for all
for all  and
and  ;
;
(c) ,
,  ;
;
(d) for some
for some  .
.
Then  and
and  converge strongly to
converge strongly to  .
.
Remark 3.17.
The conclusion of Corollary 3.16 remains true under the more general restrictions; that is, we replace (b) and (c) by the following one:
(b′) and
and  .
.
Corollary 3.18 (see [10, Theorem  ]).
]).
Let  be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space
be a nonempty closed convex subset of a uniformly convex and uniformly smooth Banach space  . Let
. Let  be a family of relatively nonexpansive mappings such that
be a family of relatively nonexpansive mappings such that  and let
and let  . For
. For  and
and  , define a sequence
, define a sequence  of
of  as follows:
as follows:

where  satisfies the following restrictions:
satisfies the following restrictions:
(i) for all
for all  and
and  ;
;
(ii) for all
for all  ,
,  for all
for all  . If
. If
(a)either  for all
for all  or
or
(b) and
and  for all
for all  .
.
then the sequence  converges strongly to
converges strongly to  .
.
Remark 3.19.
The conclusion of Corollary 3.18 remains true under the more general restrictions on  :
:
(1) are arbitrary.
are arbitrary.
(2) for all
for all  .
.
References
Matsushita S-Y, Takahashi W: Weak and strong convergence theorems for relatively nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2004,2004(1):37–47.
Alber YI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Applied Mathematics. Volume 178. Marcel Dekker, New York, NY, USA; 1996:15–50.
Takahashi W: Convex Analysis and Approximation Fixed points, Mathematical Analysis Series. Volume 2. Yokohama Publishers, Yokohama, Japan; 2000:iv+280.
Takahashi W: Nonlinear Functional Analysis, Fixed Point Theory and Its Application. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Mathematics and Its Applications. Volume 62. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990:xiv+260.
Matsushita S, Takahashi W: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. Journal of Approximation Theory 2005,134(2):257–266. 10.1016/j.jat.2005.02.007
Nilsrakoo W, Saejung S: Strong convergence to common fixed points of countable relatively quasi-nonexpansive mappings. Fixed Point Theory and Applications 2008, Article ID 312454 2008:-19 Pages.
Reich S: A weak convergence theorem for the alternating method with Bregman distances. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type, Lecture Notes in Pure and Applied Mathematics. Volume 178. Marcel Dekker, New York, NY, USA; 1996:313–318.
Kohsaka F, Takahashi W: Block iterative methods for a finite family of relatively nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2007, Article ID 21972 2007:-18 Pages.
Plubtieng S, Ungchittrakool K: Hybrid iterative methods for convex feasibility problems and fixed point problems of relatively nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2008, Article ID 583082 2008:-19 Pages.
Qin X, Cho YJ, Kang SM: Convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces. Journal of Computational and Applied Mathematics 2009,225(1):20–30. 10.1016/j.cam.2008.06.011
Su Y, Wang D, Shang M: Strong convergence of monotone hybrid algorithm for hemi-relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, Article ID 284613 2008:-8 Pages.
Su Y, Xu H: Strong convergence theorems for a common fixed point of two hemi-relatively nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5616–5628. 10.1016/j.na.2009.04.053
Wattanawitoon K, Kumam P: Strong convergence theorems by a new hybrid projection algorithm for fixed point problems and equilibrium problems of two relatively quasi-nonexpansive mappings. Nonlinear Analysis: Hybrid Systems 2009,3(1):11–20. 10.1016/j.nahs.2008.10.002
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(1):45–57. 10.1016/j.na.2007.11.031
Takahashi W, Zembayashi K: Strong convergence theorem by a new hybrid method for equilibrium problems and relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, Article ID 528476 2008:-11 Pages.
Kamimura S, Takahashi W: Strong convergence of a proximal-type algorithm in a Banach space. SIAM Journal on Optimization 2002,13(3):938–945. 10.1137/S105262340139611X
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Analysis: Theory, Methods & Applications 1991,16(12):1127–1138. 10.1016/0362-546X(91)90200-K
Nakajo K, Shimoji K, Takahashi W: Strong convergence theorems by the hybrid method for families of nonexpansive mappings in Hilbert spaces. Taiwanese Journal of Mathematics 2006,10(2):339–360.
Kohsaka F, Takahashi W: Existence and approximation of fixed points of firmly nonexpansive-type mappings in Banach spaces. SIAM Journal on Optimization 2008,19(2):824–835. 10.1137/070688717
Kim T-H, Lee H-J: Strong convergence of modified iteration processes for relatively nonexpansive mappings. Kyungpook Mathematical Journal 2008,48(4):685–703.
Acknowledgments
The authors would like to thank the referee for their comments on the manuscript. The first author is supported by grant fund under the program Strategic Scholarships for Frontier Research Network for the Ph.D. Program Thai Doctoral degree from the Office of the Higher Education Commission, Thailand, and the second author is supported by the Thailand Research Fund under Grant MRG5180146.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Boonchari, D., Saejung, S. Approximation of Common Fixed Points of a Countable Family of Relatively Nonexpansive Mappings. Fixed Point Theory Appl 2010, 407651 (2009). https://doi.org/10.1155/2010/407651
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/407651
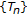 satisfies NST-condition, then
satisfies NST-condition, then  satisfies
satisfies 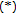 -condition.
-condition.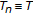 and
and  is closed, then
is closed, then  satisfies
satisfies  -condition.
-condition.