- Research Article
- Open access
- Published:
Strong Convergence Theorems of Modified Ishikawa Iterations for Countable Hemi-Relatively Nonexpansive Mappings in a Banach Space
Fixed Point Theory and Applications volume 2009, Article number: 483497 (2009)
Abstract
We prove some strong convergence theorems for fixed points of modified Ishikawa and Halpern iterative processes for a countable family of hemi-relatively nonexpansive mappings in a uniformly convex and uniformly smooth Banach space by using the hybrid projection methods. Moreover, we also apply our results to a class of relatively nonexpansive mappings, and hence, we immediately obtain the results announced by Qin and Su's result (2007), Nilsrakoo and Saejung's result (2008), Su et al.'s result (2008), and some known corresponding results in the literatures.
1. Introduction
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . A mapping
. A mapping  is said to be nonexpansive if
is said to be nonexpansive if  for all
for all  We denote by
We denote by  the set of fixed points of
the set of fixed points of  , that is
, that is  . A mapping
. A mapping  is said to be quasi-nonexpansive if
is said to be quasi-nonexpansive if  and
and  for all
for all  and
and  . It is easy to see that if
. It is easy to see that if  is nonexpansive with
is nonexpansive with  , then it is quasi-nonexpansive. Some iterative processes are often used to approximate a fixed point of a nonexpansive mapping. The Mann's iterative algorithm was introduced by Mann [1] in 1953. This iterative process is now known as Mann's iterative process, which is defined as
, then it is quasi-nonexpansive. Some iterative processes are often used to approximate a fixed point of a nonexpansive mapping. The Mann's iterative algorithm was introduced by Mann [1] in 1953. This iterative process is now known as Mann's iterative process, which is defined as

where the initial guess  is taken in
is taken in  arbitrarily and the sequence
arbitrarily and the sequence  is in the interval
is in the interval  .
.
In 1976, Halpern [2] first introduced the following iterative scheme:

see also Browder [3]. He pointed out that the conditions  and
and  are necessary in the sence that, if the iteration (1.2) converges to a fixed point of
are necessary in the sence that, if the iteration (1.2) converges to a fixed point of  , then these conditions must be satisfied.
, then these conditions must be satisfied.
In 1974, Ishikawa [4] introduced a new iterative scheme, which is defined recursively by

where the initial guess  is taken in
is taken in  arbitrarily and the sequences
arbitrarily and the sequences  and
and  are in the interval
are in the interval  .
.
Concerning a family of nonexpansive mappings it has been considered by many authors. The well-known convex feasibility problem reduces to finding a point in the intersection of the fixed point sets of a family of nonexpansive mappings; see, for example, [5]. The problem of finding an optimal point that minimizes a given cost function over common set of fixed points of a family of nonexpansive mappings is of wide interdisciplinary interest and practical importance (see [6]).
Zhang and Su [7] introduced the following implicit hybrid method for a finite family of nonexpansive mappings  in a real Hilbert space:
in a real Hilbert space:

where  ,
,  and
and  are sequences in
are sequences in  and
and  for some
for some  and
and  for some
for some  .
.
In 2008, Nakprasit et al. [8] established weak and strong convergence theorems for finding common fixed points of a countable family of nonexpansive mappings in a real Hilbert space. In the same year, Cho et al. [9] introduced the normal Mann's iterative process and proved some strong convergence theorems for a finite family nonexpansive mapping in the framework Banach spaces.
To find a common fixed point of a family of nonexpansive mappings, Aoyama et al. [10] introduced the following iterative sequence. Let  and
and

for all  , where
, where  is a nonempty closed convex subset of a Banach space,
is a nonempty closed convex subset of a Banach space,  is a sequence of
is a sequence of  and
and  is a sequence of nonexpansive mappings. Then they proved that, under some suitable conditions, the sequence
is a sequence of nonexpansive mappings. Then they proved that, under some suitable conditions, the sequence  defined by (1.5) converges strongly to a common fixed point of
defined by (1.5) converges strongly to a common fixed point of  .
.
In 2008, by using a (new) hybrid method, Takahashi et al. [11] proved the following theorem.
Theorem 1.1 (Takahashi et al. [11]).
Let  be a Hilbert space and let
be a Hilbert space and let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  . Let
. Let  and
and  be families of nonexpansive mappings of
be families of nonexpansive mappings of  into itself such that
into itself such that  and let
and let  . Suppose that
. Suppose that  satisfies the NST-condition
satisfies the NST-condition  with
with  . For
. For  and
and  , define a sequence
, define a sequence  of
of  as follows:
as follows:

where  for all
for all  and
and  is said to satisfy the NST-condition
is said to satisfy the NST-condition  with
with  if for each bounded sequence
if for each bounded sequence  ,
,  implies that
implies that  for all
for all  . Then,
. Then,  converges strongly to
converges strongly to  .
.
Note that, recently, many authors try to extend the above result from Hilbert spaces to a Banach space setting.
Let  be a real Banach space with dual
be a real Banach space with dual  . Denote by
. Denote by  the duality product. The normalized duality mapping
the duality product. The normalized duality mapping from
from  to
to  is defined by
is defined by  for all
for all  . The function
. The function  is defined by
is defined by

A mapping  is said to be hemi-relatively nonexpansive (see [12]) if
is said to be hemi-relatively nonexpansive (see [12]) if  and
and

A point  in
in  is said to be an asymptotic fixed point of
is said to be an asymptotic fixed point of  [13] if
[13] if  contains a sequence
contains a sequence  which converges weakly to
which converges weakly to  such that the strong
such that the strong  . The set of asymptotic fixed points of
. The set of asymptotic fixed points of  will be denoted by
will be denoted by  . A hemi-relatively nonexpansive mapping
. A hemi-relatively nonexpansive mapping  from
from  into itself is called relatively nonexpansive if
into itself is called relatively nonexpansive if  ; see [14–16]) for more details.
; see [14–16]) for more details.
On the other hand, Matsushita and Takahashi [17] introduced the following iteration. A sequence  defined by
defined by

where the initial guess element  is arbitrary,
is arbitrary,  is a real sequence in
is a real sequence in  ,
,  is a relatively nonexpansive mapping, and
is a relatively nonexpansive mapping, and  denotes the generalized projection from
denotes the generalized projection from  onto a closed convex subset
onto a closed convex subset  of
of  . Under some suitable conditions, they proved that the sequence
. Under some suitable conditions, they proved that the sequence  converges weakly to a fixed point of
converges weakly to a fixed point of  .
.
Recently, Kohsaka and Takahashi [18] extended iteration (1.9) to obtain a weak convergence theorem for common fixed points of a finite family of relatively nonexpansive mappings  by the following iteration:
by the following iteration:

where  and
and  with
with  , for all
, for all  . Moreover, Matsushita and Takahashi [14] proposed the following modification of iteration (1.9) in a Banach space
. Moreover, Matsushita and Takahashi [14] proposed the following modification of iteration (1.9) in a Banach space  :
:

and proved that the sequence  converges strongly to
converges strongly to  .
.
Qin and Su [15] showed that the sequence  , which is generated by relatively nonexpansive mappings
, which is generated by relatively nonexpansive mappings  in a Banach space
in a Banach space  , as follows:
, as follows:

converges strongly to 
Moreover, they also showed that the sequence  , which is generated by
, which is generated by

converges strongly to 
In 2008, Nilsrakoo and Saejung [19] used the following Mann's iterative process:

and showed that the sequence  converges strongly to a common fixed point of a countable family of relatively nonexpansive mappings.
converges strongly to a common fixed point of a countable family of relatively nonexpansive mappings.
Recently, Su et al. [12] extended the results of Qin and Su [15], Matsushita and Takahashi [14] to a class of closed hemi-relatively nonexpansive mapping. Note that, since the hybrid iterative methods presented by Qin and Su [15] and Matsushita and Takahashi [14] cannot be used for hemi-relatively nonexpansive mappings. Thus, as we know, Su et al. [12] showed their results by using the method as a monotone (CQ) hybrid method.
In this paper, motivated by Qin and Su [15], Nilsrakoo and Saejung [19], we consider the modified Ishikawa iterative (1.12) and Halpern iterative processes (1.13), which is different from those of (1.12)–(1.14), for countable hemi-relatively nonexpansive mappings. By using the shrinking projection method, some strong convergence theorems in a uniformly convex and uniformly smooth Banach space are provided. Our results extend and improve the recent results by Nilsrakoo and Saejung's result [19], Qin and Su [15], Su et al. [12], Takahashi et al.'s theorem [11], and many others.
2. Preliminaries
In this section, we will recall some basic concepts and useful well-known results.
A Banach space  is said to be strictly convex if
is said to be strictly convex if

for all  with
with  and
and  . It is said to be uniformly convex if for any two sequences
. It is said to be uniformly convex if for any two sequences  in
in  such that
such that  and
and

 holds.
holds.
Let  be the unit sphere of
be the unit sphere of  . Then the Banach space
. Then the Banach space  is said to be smooth if
is said to be smooth if

exists for each  It is said to be uniformly smooth if the limit is attained uniformly for
It is said to be uniformly smooth if the limit is attained uniformly for  . In this case, the norm of
. In this case, the norm of  is said to be Gâteaux differentiable. The space
is said to be Gâteaux differentiable. The space  is said to have uniformly Gâteaux differentiable if for each
is said to have uniformly Gâteaux differentiable if for each  , the limit (2.3) is attained uniformly for
, the limit (2.3) is attained uniformly for  . The norm of
. The norm of  is said to be uniformly Fréchet differentiable (and
is said to be uniformly Fréchet differentiable (and  is said to be uniformly smooth) if the limit (2.3) is attained uniformly for
is said to be uniformly smooth) if the limit (2.3) is attained uniformly for  .
.
In our work, the concept duality mapping is very important. Here, we list some known facts, related to the duality mapping  , as follows.
, as follows.
(a) (
( , resp.) is uniformly convex if and only if
, resp.) is uniformly convex if and only if  (
( , resp.) is uniformly smooth.
, resp.) is uniformly smooth.
(b) for each
for each  .
.
-
(c)
If
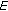 is reflexive, then
is reflexive, then 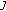 is a mapping of
is a mapping of  onto
onto 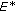 .
. -
(d)
If
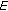 is strictly convex, then
is strictly convex, then 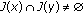 for all
for all 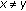 .
. -
(e)
If
 is smooth, then
is smooth, then 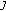 is single valued.
is single valued. -
(f)
If
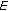 has a Fr
has a Fr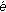 chet differentiable norm, then
chet differentiable norm, then 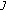 is norm to norm continuous.
is norm to norm continuous. -
(g)
If
 is uniformly smooth, then
is uniformly smooth, then  is uniformly norm to norm continuous on each bounded subset of
is uniformly norm to norm continuous on each bounded subset of 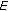 .
. -
(h)
If
 is a Hilbert space, then
is a Hilbert space, then 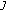 is the identity operator.
is the identity operator.
For more information, the readers may consult [20, 21].
If  is a nonempty closed convex subset of a real Hilbert space
is a nonempty closed convex subset of a real Hilbert space  and
and  is the metric projection, then
is the metric projection, then  is nonexpansive. Alber [22] has recently introduced a generalized projection operator
is nonexpansive. Alber [22] has recently introduced a generalized projection operator  in a Banach space
in a Banach space  which is an analogue representation of the metric projection in Hilbert spaces.
which is an analogue representation of the metric projection in Hilbert spaces.
The generalized projection  is a map that assigns to an arbitrary point
is a map that assigns to an arbitrary point  the minimum point of the functional
the minimum point of the functional  , that is,
, that is,  , where
, where  is the solution to the minimization problem
is the solution to the minimization problem

Notice that the existence and uniqueness of the operator  is followed from the properties of the functional
is followed from the properties of the functional  and strict monotonicity of the mapping
and strict monotonicity of the mapping  , and moreover, in the Hilbert spaces setting we have
, and moreover, in the Hilbert spaces setting we have  . It is obvious from the definition of the function
. It is obvious from the definition of the function  that
that

Remark 2.1.
If  is a strictly convex and a smooth Banach space, then for all
is a strictly convex and a smooth Banach space, then for all  ,
,  if and only if
if and only if  , see Matsushita and Takahashi [14].
, see Matsushita and Takahashi [14].
To obtain our results, following lemmas are important.
Lemma 2.2 (Kamimura and Takahashi [23]).
Let  be a uniformly convex and smooth Banach space and let
be a uniformly convex and smooth Banach space and let  . Then there exists a continuous strictly increasing and convex function
. Then there exists a continuous strictly increasing and convex function  such that
such that  and
and

for all 
Lemma 2.3 (Kamimura and Takahashi [23]).
Let  be a uniformly convex and smooth real Banach space and let
be a uniformly convex and smooth real Banach space and let  be two sequences of
be two sequences of  . If
. If  and either
and either  or
or  is bounded, then
is bounded, then  .
.
Lemma 2.4 (Alber [22]).
Let  be a nonempty closed convex subset of a smooth real Banach space E and
be a nonempty closed convex subset of a smooth real Banach space E and  . Then,
. Then,  if and only if
if and only if

Lemma 2.5 (Alber [22]).
Let  be a reflexive strict convex and smooth real Banach space, let
be a reflexive strict convex and smooth real Banach space, let  be a nonempty closed convex subset of E and let
be a nonempty closed convex subset of E and let  . Then
. Then

Lemma 2.6 (Matsushita and Takahashi [14]).
Let  be a strictly convex and smooth real Banach space, let
be a strictly convex and smooth real Banach space, let  be a closed convex subset of E, and let T be a hemi-relatively nonexpansive mapping from C into itself. Then F(T) is closed and convex.
be a closed convex subset of E, and let T be a hemi-relatively nonexpansive mapping from C into itself. Then F(T) is closed and convex.
Let  be a subset of a Banach space
be a subset of a Banach space  and let
and let  be a family of mappings from
be a family of mappings from  into
into  . For a subset
. For a subset  of
of  , one says that
, one says that
(a) satisfies condition AKTT if
satisfies condition AKTT if

(b) satisfies condition
satisfies condition  AKTT if
AKTT if

For more information, see Aoyama et al. [10].
Lemma 2.7 (Aoyama et al. [10]).
Let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  and let
and let  be a sequence of mappings from
be a sequence of mappings from  into
into  . Let
. Let  be a subset of
be a subset of  with
with  satisfying condition AKTT, then there exists a mapping
satisfying condition AKTT, then there exists a mapping  such that
such that

and 
Inspired by Lemma 2.7, Nilsrakoo and Saejung [19] prove the following results.
Lemma 2.8 (Nilsrakoo and Saejung [19]).
Let  be a reflexive and strictly convex Banach space whose norm is Fr
be a reflexive and strictly convex Banach space whose norm is Fr chet differentiable, let
chet differentiable, let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  , and let
, and let  be a sequence of mappings from
be a sequence of mappings from  into
into  . Let
. Let  be a subset of
be a subset of  with
with  satisfies condition
satisfies condition  , then there exists a mapping
, then there exists a mapping  such that
such that

and 
Lemma 2.9 (Nilsrakoo and Saejung [19]).
Let  be a reflexive and strictly convex Banach space whose norm is Fr
be a reflexive and strictly convex Banach space whose norm is Fr chet differentiable, let
chet differentiable, let  be a nonempty subset of a Banach space
be a nonempty subset of a Banach space  and let
and let  be a sequence of mappings from
be a sequence of mappings from  into
into  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Then there exists a mapping
. Then there exists a mapping  such that
such that

3. Modified Ishikawa Iterative Scheme
In this section, we establish the strong convergence theorems for finding common fixed points of a countable family of hemi-relatively nonexpansive mappings in a uniformly convex and uniformly smooth Banach space. It is worth mentioning that our main theorem generalizes recent theorems by Su et al. [12] from relatively nonexpansive mappings to a more general concept. Moreover, our results also improve and extend the corresponding results of Nilsrakoo and Saejung [19]. In order to prove the main result, we recall a concept as follows. An operator  in a Banach space is closed if
in a Banach space is closed if  and
and  , then
, then  .
.
Theorem 3.1.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of hemi-relatively nonexpansive mappings from
be a sequence of hemi-relatively nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  and
and  are sequences in
are sequences in  such that
such that  and
and  and let a sequence
and let a sequence  in
in  by the following algorithm be:
by the following algorithm be:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . If
. If  is uniformly continuous for all
is uniformly continuous for all  , then
, then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Proof.
We first show that  is closed and convex for each
is closed and convex for each  . Obviously, from the definition of
. Obviously, from the definition of  , we see that
, we see that  is closed for each
is closed for each  . Now we show that
. Now we show that  is convex for any
is convex for any  . Since
. Since

this implies that  is a convex set. Next, we show that
is a convex set. Next, we show that  for all
for all  . Indeed, let
. Indeed, let  , we have
, we have


Substituting (3.4) into (3.3), we have

This means that,  for all
for all  . Consequently, the sequence
. Consequently, the sequence  is well defined. Moreover, since
is well defined. Moreover, since  and
and  , we get
, we get

for all  . Therefore,
. Therefore,  is nondecreasing.
is nondecreasing.
By the definition of  and Lemma 2.5, we have
and Lemma 2.5, we have

for all  . Thus,
. Thus,  is a bounded sequence. Moreover, by (2.5), we know that
is a bounded sequence. Moreover, by (2.5), we know that  is bounded. So,
is bounded. So, 
 exists. Again, by Lemma 2.5, we have
exists. Again, by Lemma 2.5, we have

for all  . Thus,
. Thus,  as
as  .
.
Next, we show that  is a Cauchy sequence. Using Lemma 2.2, for
is a Cauchy sequence. Using Lemma 2.2, for  such that
such that  , we have
, we have

where  is a continuous stricly increasing and convex function with
is a continuous stricly increasing and convex function with  . Then the properties of the function
. Then the properties of the function  yield that
yield that  is a Cauchy sequence. Thus, we can say that
is a Cauchy sequence. Thus, we can say that  converges strongly to
converges strongly to  for some point
for some point  in
in  . However, since
. However, since 
 and
and  is bounded, we obtain
is bounded, we obtain

Therefore  as
as  .
.
Since  , from the definition of
, from the definition of  , we have
, we have

for all  . Thus
. Thus

By using Lemma 2.3, we also have

Since  is uniformly norm-to-norm continuous on bounded sets, we have
is uniformly norm-to-norm continuous on bounded sets, we have

For each  we observe that
we observe that

It follows that

By (3.14) and  , we obtain
, we obtain

Since  is uniformly norm-to-norm continuous on bounded sets, we have
is uniformly norm-to-norm continuous on bounded sets, we have

By (3.13), we have

Since  is uniformly continuous, by (3.13) and (3.18), we obtain
is uniformly continuous, by (3.13) and (3.18), we obtain

as  , and so
, and so

Based on the hypothesis, we now consider the following two cases.
Case 1.
 satisfies condition
satisfies condition  . Applying Lemma 2.8 to get
. Applying Lemma 2.8 to get

Case 2.
 satisfies condition AKTT. Apply Lemma 2.7 to get
satisfies condition AKTT. Apply Lemma 2.7 to get

Hence

Therefore, from the both two cases, we have

Since  is closed and
is closed and  , we have
, we have  Moreover, by (3.7), we obtain
Moreover, by (3.7), we obtain

for all  . Therefore,
. Therefore,  This completes the proof.
This completes the proof.
Since every relatively nonexpansive mapping is a hemi-relatively nonexpansive mapping, we obtain the following result for a countable family of relatively nonexpansive mappings of modified Ishikawa iterative process.
Corollary 3.2.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of relatively nonexpansive mappings from
be a sequence of relatively nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  and
and  are sequences in
are sequences in  such that
such that  and
and  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . If
. If  is uniformly continuous for all
is uniformly continuous for all  , then
, then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Theorem 3.3.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of hemi-relatively nonexpansive mappings from
be a sequence of hemi-relatively nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
In Theorem 3.1, if  for all
for all  then (3.1) reduced to (3.28).
then (3.1) reduced to (3.28).
Corollary 3.4.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of relatively nonexpansive mappings from
be a sequence of relatively nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . Then
. Then  converges strongly to
converges strongly to  .
.
Notice that every uniformly continuous mapping must be a continuous and closed mapping. Then setting  for all
for all  , in Theorems 3.1 and 3.3, we immediately obtain the following results.
, in Theorems 3.1 and 3.3, we immediately obtain the following results.
Corollary 3.5.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a closed hemi-relatively nonexpansive mapping such that
be a closed hemi-relatively nonexpansive mapping such that  . Assume that
. Assume that  and
and  are sequences in
are sequences in  such that
such that  and
and  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . If
. If  is uniformly continuous, then
is uniformly continuous, then  converges strongly to
converges strongly to  .
.
Corollary 3.6.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a closed relatively nonexpansive mapping such that
be a closed relatively nonexpansive mapping such that  . Assume that
. Assume that  and
and  are sequences in
are sequences in  such that
such that  and
and  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . If
. If  is uniformly continuous, then
is uniformly continuous, then  converges strongly to
converges strongly to  .
.
Proof.
Since a closed relatively nonexpansive mapping is a closed hemi-relatively one, Corollary 3.6 is implied by Corollary 3.5.
Corollary 3.7.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a closed hemi-relatively nonexpansive mapping from
be a closed hemi-relatively nonexpansive mapping from  into itself such that
into itself such that  . Assume that
. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Then
. Then  converges strongly to
converges strongly to  .
.
Corollary 3.8.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a closed relatively nonexpansive mapping from
be a closed relatively nonexpansive mapping from  into itself such that
into itself such that  . Assume that
. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Then
. Then  converges strongly to
converges strongly to  .
.
Similarly, as in the proof of Theorem 3.1, we obtain the following results.
Theorem 3.9.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of hemi-relatively nonexpansive mappings from
be a sequence of hemi-relatively nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  and
and  are sequences in
are sequences in  such that
such that  and
and  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . If
. If  is uniformly continuous for all
is uniformly continuous for all  , then
, then  converges strongly to
converges strongly to  , where
, where  is the generalized projection from
is the generalized projection from  onto
onto  .
.
Corollary 3.10.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be closed hemi-relatively nonexpansive mappings from
be closed hemi-relatively nonexpansive mappings from  into itself such that
into itself such that  . Assume that
. Assume that  and
and  are sequences in
are sequences in  such that
such that  and
and  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . If
. If  is uniformly continuous, then
is uniformly continuous, then  converges strongly to
converges strongly to  .
.
Theorem 3.11.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of relatively nonexpansive mappings from
be a sequence of relatively nonexpansive mappings from  into itself such that
into itself such that  is a nonempty. Assume that
is a nonempty. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
Putting  , for all
, for all  , in Theorem 3.9 we immediately obtain Theorem 3.11.
, in Theorem 3.9 we immediately obtain Theorem 3.11.
Corollary 3.12.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be closed hemi-relatively nonexpansive mappings from
be closed hemi-relatively nonexpansive mappings from  into itself such that
into itself such that  . Assume that
. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Then
. Then  converges strongly to
converges strongly to  .
.
Remark 3.13.
Our results extend and improve the corresponding results in the following senses.
-
(i)
Corollary 3.10 improves Theorem 2.1 of Qin and Su [15] from relatively nonexpansive mappings to more general hemi-relatively nonexpansive mappings.
-
(ii)
Theorem 3.11 improves the algorithm in Theorem 3.1 of Nilsakoo and Saejung [19] from the Mann iteration process to modify Ishikawa iteration process and from countable relatively nonexpansive mappings to more general countable hemi-relatively nonexpansive mappings; that is, we relax the strong restriction
 . From (i) and (ii), it means that we relax the strongly restriction as
. From (i) and (ii), it means that we relax the strongly restriction as 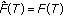 from the assumption.
from the assumption.
-
(iii)
Corollary 3.12 improves Theorem 3.1 of Matsushita and Takahashi [14] from relatively nonexpansive mappings to more general hemi-relatively nonexpansive mappings in a Banach space.
4. Halpern Iterative Scheme
In this section, we prove the strong convergence theorems for finding common fixed points of a countable family of hemi-relatively nonexpansive mappings, which can be viewed as a generalization of the recently result of [15, Theorem 2.2].
Theorem 4.1.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of hemi-relatively nonexpansive mappings from
be a sequence of hemi-relatively nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
As in the proof of Theorem 3.1, we have that  is closed and convex for each
is closed and convex for each  .
.
Next, we show that  for all
for all  . Indeed, let
. Indeed, let  , we have
, we have

This means that,  for all
for all  From Theorem 3.1, we obtain
From Theorem 3.1, we obtain  and
and  exists. Since
exists. Since  and hence
and hence  , we also get
, we also get

for all  . Since
. Since  , thus,
, thus,  as
as  .
.
By using the same argument as in Theorem 3.1, we obtain that  is a Cauchy sequence, thus
is a Cauchy sequence, thus  converges strongly to
converges strongly to  for some point
for some point  in
in  . By using Lemma 2.3, we also have
. By using Lemma 2.3, we also have

Since  is uniformly norm-to-norm continuous on bounded sets, we have
is uniformly norm-to-norm continuous on bounded sets, we have

Observe that

this gives

By (4.5) and  , we obtain
, we obtain  Since
Since  is uniformly norm-to-norm continuous on bounded sets, we have
is uniformly norm-to-norm continuous on bounded sets, we have

It follows from (4.4) that  as
as  , and since
, and since  is uniformly norm-to-norm continuous on bounded sets, we get
is uniformly norm-to-norm continuous on bounded sets, we get  From the conditions
From the conditions  , AKTT, Lemmas 2.7 and 2.8, by using the same line as in the proof of Theorem 3.1, the both two cases, we know that
, AKTT, Lemmas 2.7 and 2.8, by using the same line as in the proof of Theorem 3.1, the both two cases, we know that

Finally, we prove that  , where
, where  . Let
. Let  be a subsequence of
be a subsequence of  such that
such that  Replacing
Replacing  , from
, from  and
and  , we have
, we have  . On the other hand, from weakly lower semicontinuity of the norm, we have
. On the other hand, from weakly lower semicontinuity of the norm, we have

From the definition of  , since
, since  , we have
, we have  This implies
This implies  . Using the Kadec-Klee property ([24]) of the space
. Using the Kadec-Klee property ([24]) of the space  , we obtain that
, we obtain that  converges strongly to
converges strongly to  . Since
. Since  is an arbitrary weakly convergent sequence of
is an arbitrary weakly convergent sequence of  , we can conclude that
, we can conclude that  convergence strongly to
convergence strongly to 
Corollary 4.2.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a closed hemi-relatively nonexpansive mapping from
be a closed hemi-relatively nonexpansive mapping from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is a sequence in
is a sequence in  such that
such that 
 and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
By setting  for all
for all  , we immediately obtain the result.
, we immediately obtain the result.
Since every relatively nonexpansive mapping is a hemi-relatively nonexpansive mapping, we immediately obtain the following corollaries.
Corollary 4.3.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of relatively nonexpansive mappings from
be a sequence of relatively nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is a sequence in
is a sequence in  such that
such that 
 and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . Then
. Then  converges strongly to
converges strongly to  .
.
Corollary 4.4.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a closed relatively nonexpansive mapping from
be a closed relatively nonexpansive mapping from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Then
. Then  converges strongly to
converges strongly to  .
.
Similarly, as in the proof of Theorem 4.1, we obtain the following result.
Theorem 4.5.
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of hemi-relatively nonexpansive mappings from
be a sequence of hemi-relatively nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies either condition AKTT or condition
satisfies either condition AKTT or condition  . Let
. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . Then
. Then  converges strongly to
converges strongly to  .
.
If  , then Theorem 4.5 reduces to the following corollary.
, then Theorem 4.5 reduces to the following corollary.
Corollary 4.6 (see [15, Theorem 2.2]).
Let  be a uniformly convex and uniformly smooth Banach space and let
be a uniformly convex and uniformly smooth Banach space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a closed relatively nonexpansive mapping from
be a closed relatively nonexpansive mapping from  into itself such that
into itself such that  . Assume that
. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  , where
, where  is the single-valued duality mapping on
is the single-valued duality mapping on  . Then
. Then  converges strongly to
converges strongly to  .
.
5. Some Applications to Hilbert Spaces
It is well known that, in the Hilbert space setting, the concepts of hemi-relatively nonexpansive mappings and quasi-nonexpansive mappings are the equivalent. Thus, the following results can be obtained.
Theorem 5.1.
Let  be a Hilbert space and let
be a Hilbert space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of quasi-nonexpansive mappings from
be a sequence of quasi-nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  and
and  are sequences in
are sequences in  such that
such that  and
and  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies condition AKTT. Let
satisfies condition AKTT. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by 

 for all
for all  and suppose that
and suppose that  is closed and
is closed and  . If
. If  is uniformly continuous for all
is uniformly continuous for all  , then
, then  converges strongly to
converges strongly to  .
.
Proof.
Since  is an identity operator, we have
is an identity operator, we have

for every  Therefore
Therefore

for every  and
and  Hence,
Hence,  is quasi-nonexpansive if and only if
is quasi-nonexpansive if and only if  is hemi-relatively nonexpansive. Then, by Theorem 3.1, we obtain the result.
is hemi-relatively nonexpansive. Then, by Theorem 3.1, we obtain the result.
Theorem 5.2.
Let  be a Hilbert space and let
be a Hilbert space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of quasi-nonexpansive mappings from
be a sequence of quasi-nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is sequence in
is sequence in  such that
such that 
 and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies condition AKTT. Let
satisfies condition AKTT. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . Then
. Then  converges strongly to
converges strongly to  .
.
Proof.
In Theorem 5.1 setting  for all
for all  , then (5.1) reduces to (5.4).
, then (5.1) reduces to (5.4).
Theorem 5.3.
Let  be a Hilbert space and let
be a Hilbert space and let  be a nonempty bounded closed convex subset of
be a nonempty bounded closed convex subset of  . Let
. Let  be a sequence of quasi-nonexpansive mappings from
be a sequence of quasi-nonexpansive mappings from  into itself such that
into itself such that  is nonempty. Assume that
is nonempty. Assume that  is a sequence in
is a sequence in  such that
such that  and let a sequence
and let a sequence  in
in  be defined by the following algorithm:
be defined by the following algorithm:

for  . Suppose that for each bounded subset
. Suppose that for each bounded subset  of
of  , the ordered pair
, the ordered pair  satisfies condition AKTT. Let
satisfies condition AKTT. Let  be the mapping from
be the mapping from  into itself defined by
into itself defined by  for all
for all  and suppose that
and suppose that  is closed and
is closed and  . Then
. Then  converges strongly to
converges strongly to  .
.
References
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Halpern B: Fixed points of nonexpanding maps. Bulletin of the American Mathematical Society 1967, 73: 957–961. 10.1090/S0002-9904-1967-11864-0
Browder FE: Fixed-point theorems for noncompact mappings in Hilbert space. Proceedings of the National Academy of Sciences of the United States of America 1965, 53: 1272–1276. 10.1073/pnas.53.6.1272
Ishikawa S: Fixed points by a new iteration method. Proceedings of the American Mathematical Society 1974, 44: 147–150. 10.1090/S0002-9939-1974-0336469-5
Bauschke HH, Borwein JM: On projection algorithms for solving convex feasibility problems. SIAM Review 1996,38(3):367–426. 10.1137/S0036144593251710
Youla DC: Mathematical theory of image restoration by the method of convex projections. In Image Recovery: Theory and Application. Edited by: Stark H. Academic Press, Orlando, Fla, USA; 1987:29–77.
Zhang F, Su Y: Strong convergence of modified implicit iteration processes for common fixed points of nonexpansive mappings. Fixed Point Theory and Applications 2007, Article ID 48174, 2007:-9.
Nakprasit K, Nilsrakoo W, Saejung S: Weak and strong convergence theorems of an implicit iteration process for a countable family of nonexpansive mappings. Fixed Point Theory and Applications 2008, Article ID 732193, 2008:-18.
Cho YJ, Kang SM, Qin X: Convergence theorems of fixed points for a finite family of nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2008, Article ID 856145, 2008:-7.
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2007,67(2):2350–2360.
Takahashi W, Takeuchi Y, Kubota R: Strong convergence theorems by hybrid methods for families of nonexpansive mappings in Hilbert spaces. Journal of Mathematical Analysis and Applications 2008,341(1):276–286. 10.1016/j.jmaa.2007.09.062
Su Y, Wang D, Shang M: Strong convergence of monotone hybrid algorithm for hemi-relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, Article ID 284613, 2008:-8.
Butnariu D, Reich S, Zaslavski AJ: Asymptotic behavior of relatively nonexpansive operators in Banach spaces. Journal of Mathematical Analysis and Applications 2001,7(2):151–174.
Matsushita S, Takahashi W: A strong convergence theorem for relatively nonexpansive mappings in a Banach space. Journal of Approximation Theory 2005,134(2):257–266. 10.1016/j.jat.2005.02.007
Qin X, Su Y: Strong convergence theorems for relatively nonexpansive mappings in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2007,67(6):1958–1965. 10.1016/j.na.2006.08.021
Takahashi W, Zembayashi K: Strong convergence theorem by a new hybrid method for equilibrium problems and relatively nonexpansive mappings. Fixed Point Theory and Applications 2008, Article ID 528476, 2008:-11.
Matsushita S, Takahashi W: Weakly and strong convergence theorems for relatively nonexpansive mappings in a Banach space. Fixed Point Theory and Applications 2004,2004(1):37–47. 10.1155/S1687182004310089
Kohsaka F, Takahashi W: Block iterative methods for a finite family of relatively nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2007, Article ID 21972, 2007:-18.
Nilsrakoo W, Saejung S: Strong convergence to common fixed points of countable relatively quasi-nonexpansive mappings. Fixed Point Theory and Applications 2008, Article ID 312454, 2008:-19.
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems, Mathematics and Its Applications. Volume 62. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1990.
Takahashi W: Nonlinear Functional Analysis: Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000.
Alber YaI: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Volume 178. Edited by: Kartsatos AG. Marcel Dekker, New York, NY, USA; 1996:15–50.
Kamimura S, Takahashi W: Strong convergence of a proximal-type algorithm in a Banach space. SIAM Journal on Optimization 2002,13(3):938–945. 10.1137/S105262340139611X
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990.
Acknowledgments
The authors would like to thank the referees for the valuable suggestions which helped to improve this manuscript. This research is supported by the Centre of Excellence in Mathematics, the Commission on Higher Education, Thailand.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Petrot, N., Wattanawitoon, K. & Kumam, P. Strong Convergence Theorems of Modified Ishikawa Iterations for Countable Hemi-Relatively Nonexpansive Mappings in a Banach Space. Fixed Point Theory Appl 2009, 483497 (2009). https://doi.org/10.1155/2009/483497
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2009/483497
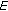 is reflexive, then
is reflexive, then 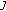 is a mapping of
is a mapping of  onto
onto 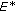 .
.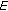 is strictly convex, then
is strictly convex, then 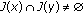 for all
for all 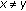 .
. is smooth, then
is smooth, then 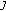 is single valued.
is single valued.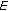 has a Fr
has a Fr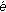 chet differentiable norm, then
chet differentiable norm, then 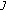 is norm to norm continuous.
is norm to norm continuous. is uniformly smooth, then
is uniformly smooth, then  is uniformly norm to norm continuous on each bounded subset of
is uniformly norm to norm continuous on each bounded subset of 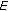 .
. is a Hilbert space, then
is a Hilbert space, then 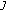 is the identity operator.
is the identity operator. . From (i) and (ii), it means that we relax the strongly restriction as
. From (i) and (ii), it means that we relax the strongly restriction as 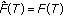 from the assumption.
from the assumption.