- Research Article
- Open access
- Published:
Compact Weighted Composition Operators and Fixed Points in Convex Domains
Fixed Point Theory and Applications volume 2007, Article number: 028750 (2007)
Abstract
Let  be a bounded, convex domain in
be a bounded, convex domain in  , and suppose that
, and suppose that  is holomorphic. Assume that
is holomorphic. Assume that  is analytic, bounded away from zero toward the boundary of
is analytic, bounded away from zero toward the boundary of  , and not identically zero on the fixed point set of
, and not identically zero on the fixed point set of  . Suppose also that the weighted composition operator
. Suppose also that the weighted composition operator  given by
given by  is compact on a holomorphic, functional Hilbert space (containing the polynomial functions densely) on
is compact on a holomorphic, functional Hilbert space (containing the polynomial functions densely) on  with reproducing kernel
with reproducing kernel  satisfying
satisfying  as
as  . We extend the results of J. Caughran/H. Schwartz for unweighted composition operators on the Hardy space of the unit disk and B. MacCluer on the ball by showing that
. We extend the results of J. Caughran/H. Schwartz for unweighted composition operators on the Hardy space of the unit disk and B. MacCluer on the ball by showing that  has a unique fixed point in
has a unique fixed point in  . We apply this result by making a reasonable conjecture about the spectrum of
. We apply this result by making a reasonable conjecture about the spectrum of  based on previous results.
based on previous results.
References
Caughran JG, Schwartz HJ: Spectra of compact composition operators. Proceedings of the American Mathematical Society 1975,51(1):127–130. 10.1090/S0002-9939-1975-0377579-7
Cowen CC, MacCluer BD: Composition Operators on Spaces of Analytic Functions, Studies in Advanced Mathematics. CRC Press, Boca Raton, Fla, USA; 1995:xii+388.
MacCluer BD: Spectra of compact composition operators on
 . Analysis 1984,4(1–2):87–103.
. Analysis 1984,4(1–2):87–103.Clahane DD: Spectra of compact composition operators over bounded symmetric domains. Integral Equations and Operator Theory 2005,51(1):41–56. 10.1007/s00020-003-1250-z
Gunatillake G: Spectrum of a compact weighted composition operator. Proceedings of the American Mathematical Society 2007,135(2):461–467. 10.1090/S0002-9939-06-08497-8
Clifford JH, Dabkowski MG: Singular values and Schmidt pairs of composition operators on the Hardy space. Journal of Mathematical Analysis and Applications 2005,305(1):183–196. 10.1016/j.jmaa.2004.11.014
Shapiro JH, Smith W: Hardy spaces that support no compact composition operators. Journal of Functional Analysis 2003,205(1):62–89. 10.1016/S0022-1236(03)00215-5
Hammond C: On the norm of a composition operator, Ph.D. thesis. University of Virginia, Charlottesville, Va, USA; 2003.
Abate M: Iteration Theory of Holomorphic Maps on Taut Manifolds, Research and Lecture Notes in Mathematics. Complex Analysis and Geometry. Mediterranean Press, Rende, Italy; 1989:xvii+417.
Vigué J-P: Points fixes d'applications holomorphes dans un domaine born convexe de
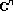 [Fixed points of holomorphic mappings in a bounded convex domain in
[Fixed points of holomorphic mappings in a bounded convex domain in 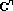 ]. Transactions of the American Mathematical Society 1985,289(1):345–353.
]. Transactions of the American Mathematical Society 1985,289(1):345–353.Conway JB: A Course in Functional Analysis, Graduate Texts in Mathematics. Volume 96. 2nd edition. Springer, New York, NY, USA; 1990:xvi+399.
Krantz SG: Geometric Analysis and Function Spaces, CBMS Regional Conference Series in Mathematics. Volume 81. American Mathematical Society, Washington, DC, USA; 1993:xii+202.
Vigué J-P: Sur les points fixes d'applications holomorphes [On the fixed points of holomorphic mappings]. Comptes Rendus de l'Académie des Sciences. Série I. Mathématique 1986,303(18):927–930.
Huang XJ: A non-degeneracy property of extremal mappings and iterates of holomorphic self-mappings. Annali della Scuola Normale Superiore di Pisa. Classe di Scienze. Serie IV 1994,21(3):399–419.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Clahane, D.D. Compact Weighted Composition Operators and Fixed Points in Convex Domains. Fixed Point Theory Appl 2007, 028750 (2007). https://doi.org/10.1155/2007/28750
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2007/28750
 . Analysis 1984,4(1–2):87–103.
. Analysis 1984,4(1–2):87–103.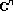 [Fixed points of holomorphic mappings in a bounded convex domain in
[Fixed points of holomorphic mappings in a bounded convex domain in 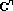 ]. Transactions of the American Mathematical Society 1985,289(1):345–353.
]. Transactions of the American Mathematical Society 1985,289(1):345–353.