- Research Article
- Open access
- Published:
Linking Contractive Self-Mappings and Cyclic Meir-Keeler Contractions with Kannan Self-Mappings
Fixed Point Theory and Applications volume 2010, Article number: 572057 (2010)
Abstract
Some mutual relations between p-cyclic contractive self-mappings, p-cyclic Kannan self-mappings, and Meir-Keeler p-cyclic contractions are stated. On the other hand, related results about the existence of the best proximity points and existence and uniqueness of fixed points are also formulated.
1. Introduction
In the last years, important attention is being devoted to extend the Fixed Point Theory by weakening the conditions on both the maps and the sets where those maps operate [1, 2]. For instance, every nonexpansive self-mappings on weakly compact subsets of a metric space have fixed points if the weak fixed point property holds [1]. Further, increasing research interest relies on the generalization of Fixed Point Theory to more general spaces than the usual metric spaces such as, for instance, ordered or partially ordered spaces (see, e.g., [3–5]). Also, important fields of application of Fixed Point Theory exist nowadays in the investigation of the stability of complex continuous-time and discrete-time dynamic systems. The theory has been focused, in particular, on systems possessing internal lags, those being described by functional differential equations, those being characterized as hybrid dynamic systems and those being described by coupled continuous-time and discrete-time dynamics, [6–10]. On the other hand, Meir-Keeler self-mappings have received important attention in the context of Fixed Point Theory perhaps due to the associated relaxing in the required conditions for the existence of fixed points compared with the usual contractive mappings [11–14]. It also turns out from their definition that such self-mappings are less restrictive than strict contractive self-mappings so that their associated formalism is applicable to a wider class of real-life problems. Another interest of such self-mappings is their usefulness as a formal tool for the study of  (
( 2)-cyclic contractions, even in the eventual case that the involved subsets of the metric space under study do not intersect, [12] so that there is no fixed point. In such a case, the usual role of fixed points is played by the best proximity points between adjacent subsets in the metric space. The underlying idea is that the best proximity points are fixed points if such subsets intersect while they play a close role to fixed points otherwise. On the other hand, there are also close links between contractive self-mappings and Kannan self-mappings [2, 15–17] with constant
2)-cyclic contractions, even in the eventual case that the involved subsets of the metric space under study do not intersect, [12] so that there is no fixed point. In such a case, the usual role of fixed points is played by the best proximity points between adjacent subsets in the metric space. The underlying idea is that the best proximity points are fixed points if such subsets intersect while they play a close role to fixed points otherwise. On the other hand, there are also close links between contractive self-mappings and Kannan self-mappings [2, 15–17] with constant  (referred to in the following as
(referred to in the following as  Kannan self-mappings). In fact,
Kannan self-mappings). In fact,  -Kannan self-mappings are contractive for values of the contraction constant being less than 1/3 [17].
-Kannan self-mappings are contractive for values of the contraction constant being less than 1/3 [17].
The objective of this paper is to formulate some connections between  -cyclic contractive self-mappings,
-cyclic contractive self-mappings,  -cyclic Meir-Keeler contractions, and
-cyclic Meir-Keeler contractions, and  -cyclic
-cyclic  -Kannan self-mappings. In particular, the existence and uniqueness of potential fixed points and also the best proximity points are investigated. The importance of cyclic maps in some problems as, for instance, in the case that a controlled state-solution trajectory of a dynamic system has to be driven from a set to its adjacent one in a certain time due to technical requirements, is well known. Consider a metric space
-Kannan self-mappings. In particular, the existence and uniqueness of potential fixed points and also the best proximity points are investigated. The importance of cyclic maps in some problems as, for instance, in the case that a controlled state-solution trajectory of a dynamic system has to be driven from a set to its adjacent one in a certain time due to technical requirements, is well known. Consider a metric space  and a self-mapping
and a self-mapping  such that
such that  and
and  where
where  and
and  are nonempty subsets of
are nonempty subsets of  . Then,
. Then,  is a 2-cyclic self-mapping what is said to be a 2-cyclic
is a 2-cyclic self-mapping what is said to be a 2-cyclic  -contraction self-mapping if it satisfies in addition
-contraction self-mapping if it satisfies in addition

for some real  . The best proximity point is some
. The best proximity point is some  such that
such that  . It turns out that if
. It turns out that if  , then
, then  ; that is,
; that is,  is a fixed point of
is a fixed point of  since
since  [11–13]. If
[11–13]. If  , then
, then  ;
;  and
and  is a 2-cyclic nonexpansive self-mapping [12]. Nonexpansive mappings, in general, have received important attention in the last years. For instance, two hybrid methods are used in [18] to prove some strong convergence theorems. Those theorems are used to find a common element of the zero point set of a maximal monotone operator and the fixed point set of a relatively nonexpansive mapping in a Banach space. The concept of a strongly relatively nonexpansive sequence in a Banach space is given in [19]. The associate properties are investigated and applied approximating a common fixed point of a countable family of relatively nonexpansive mappings in uniformly convex and uniformly smooth Banach spaces. Also, the so-called
is a 2-cyclic nonexpansive self-mapping [12]. Nonexpansive mappings, in general, have received important attention in the last years. For instance, two hybrid methods are used in [18] to prove some strong convergence theorems. Those theorems are used to find a common element of the zero point set of a maximal monotone operator and the fixed point set of a relatively nonexpansive mapping in a Banach space. The concept of a strongly relatively nonexpansive sequence in a Banach space is given in [19]. The associate properties are investigated and applied approximating a common fixed point of a countable family of relatively nonexpansive mappings in uniformly convex and uniformly smooth Banach spaces. Also, the so-called  -times reasonable expansive and their properties self-mappings are investigated in [20].
-times reasonable expansive and their properties self-mappings are investigated in [20].
1.1. Notation
 ,
,  ,
,  , and
, and  are the sets of nonnegative real and integer numbers and those of positive real and integer numbers, respectively,
are the sets of nonnegative real and integer numbers and those of positive real and integer numbers, respectively,

 is the set of fixed points of a
is the set of fixed points of a  -cyclic self-mapping
-cyclic self-mapping  in a nonempty subset
in a nonempty subset  of a metric space
of a metric space  .
.
 is the set of the best proximity points in a subset
is the set of the best proximity points in a subset  of a
of a  -cyclic self-mapping
-cyclic self-mapping  on
on  , namely, the union of a collection of nonempty subsets of a metric space
, namely, the union of a collection of nonempty subsets of a metric space  which do not intersect.
which do not intersect.
Contractive self-mappings with constant  and Kannan self-mappings with constant
and Kannan self-mappings with constant  are referred to as
are referred to as  -contractions and
-contractions and  -Kannan self-mappings, respectively.
-Kannan self-mappings, respectively.
 (referred to as "not
(referred to as "not  ") is the negation of a logic proposition
") is the negation of a logic proposition  .
.
2. About 2-Cyclic 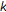 -Contraction, 2-Cyclic
-Contraction, 2-Cyclic  -Kannan Self-Mappings, Contractions of Meir-Keeler Type, and Some Mutual Relationships
-Kannan Self-Mappings, Contractions of Meir-Keeler Type, and Some Mutual Relationships
The definition of  -Kannan self-mappings
-Kannan self-mappings  is as follows:
is as follows:

for some real  [14, 15]. Let us extend the above concept in a natural way to 2-cyclic Kannan self-mappings by considering the definition of 2-cyclic
[14, 15]. Let us extend the above concept in a natural way to 2-cyclic Kannan self-mappings by considering the definition of 2-cyclic  -contractions (1.1) as follows.
-contractions (1.1) as follows.
Definition 2.1.
Consider a metric space  and a self-mapping
and a self-mapping  such that
such that  and
and  where
where  and
and  are nonempty subsets of
are nonempty subsets of  . Then
. Then  is a 2-cyclic
is a 2-cyclic  -Kannan self-mapping for some real
-Kannan self-mapping for some real  if it satisfies
if it satisfies

for some  . Definition 2.1 is a natural counterpart of (2.1) for
. Definition 2.1 is a natural counterpart of (2.1) for  -Kannan self-mappings by taking into account the definition of a 2-cyclic
-Kannan self-mappings by taking into account the definition of a 2-cyclic  -contraction in (1.1).
-contraction in (1.1).
Remark 2.2.
Let  be a metric space and let
be a metric space and let  be a 2-cyclic
be a 2-cyclic  -contraction self-mapping with
-contraction self-mapping with  and
and  being nonempty nondisjoint subsets of
being nonempty nondisjoint subsets of  . It turns out that
. It turns out that  is also a contractive mapping with constant
is also a contractive mapping with constant  .
.
Contraction self-mappings can also be 2-cyclic  -Kannan self-mappings and vice-versa as addressed in the two following results:
-Kannan self-mappings and vice-versa as addressed in the two following results:
Proposition 2.3.
Assume that  is a 2-cyclic
is a 2-cyclic  -contraction self-mapping with
-contraction self-mapping with  . Then,
. Then,  is also a 2-cyclic
is also a 2-cyclic  -Kannan self-mapping,
-Kannan self-mapping,  .
.
Proof.
The following inequalities follow from (1.1) and the triangle inequality of the distance map  :
:

for some  , what leads to
, what leads to

for  ,
,  ,
,  . Thus,
. Thus,  is a 2-cyclic
is a 2-cyclic  -Kannan self-mapping from Definition 2.1 for
-Kannan self-mapping from Definition 2.1 for  if
if  . The proof is complete.
. The proof is complete.
Proposition 2.4.
Assume that  and
and  are closed disjoint nonempty bounded simply connected sets with
are closed disjoint nonempty bounded simply connected sets with  and
and  for some
for some  ,
,  . Assume also that
. Assume also that  is a 2-cyclic
is a 2-cyclic  -Kannan self-mapping with
-Kannan self-mapping with  and
and  subject to the constraints
subject to the constraints  and
and  with
with  . Then,
. Then,  is also a 2-cyclic
is also a 2-cyclic  -contraction self-mapping for any real constant
-contraction self-mapping for any real constant  .
.
Proof.
Since  is a 2-cyclic
is a 2-cyclic  -Kannan self-mapping then from Definition 2.1, it follows that
-Kannan self-mapping then from Definition 2.1, it follows that

Also, one has that  ,
,  , since
, since  ;
;  . Choosing
. Choosing  and
and  such that
such that  , the triangle inequality for the distance map yields
, the triangle inequality for the distance map yields

so that one has since  :
:

provided that  under the necessary conditions
under the necessary conditions  and
and  . The above derivation remains valid by interchanging the roles of the sets
. The above derivation remains valid by interchanging the roles of the sets  and
and  since
since  .
.
The following two results are direct.
Corollary 2.5.
Proposition 2.4 holds "mutatis-mutandis" if either  or
or  is an open set.
is an open set.
Proof.
It follows under the same reasoning by taking  in
in  if
if  is open and
is open and  in
in  if
if  is open.
is open.
Corollary 2.6.
Proposition 2.4 and Corollary 2.5 cannot be fulfilled for any  if
if  .
.
Proof.
It is direct since  and
and  and
and  are infinite.
are infinite.
Definition 2.7 (see [12]).
A 2-cyclic contraction self-mapping  is of Meir-Keeler type if for any given
is of Meir-Keeler type if for any given  ,
,  such that
such that

The subsequent result is concerned with 2-cyclic contraction self-mappings of Meir-Keeler type
Proposition 2.8.
Assume that  is a 2-cyclic contraction self-mapping of Meir-Keeler type. Then, the following properties hold:
is a 2-cyclic contraction self-mapping of Meir-Keeler type. Then, the following properties hold:
(i)If  , then
, then  and
and  ;
;  , that is, all the best proximity points are also fixed points.
, that is, all the best proximity points are also fixed points.
(ii)If  , then either
, then either  or
or  ;
;  .
.
Also,  such that
such that

Proof.
Note from (2.8) that

for some  ;
;  . Define
. Define  ;
;  . Since
. Since  is a 2-cyclic contraction self-mapping of Meir-Keeler type, one has proceeding recursively with (2.10)
is a 2-cyclic contraction self-mapping of Meir-Keeler type, one has proceeding recursively with (2.10)

so that (2.10) together with the constraint  implies that
implies that

If, in addition,  , that is,
, that is,  , then
, then  (otherwise,
(otherwise,  ;
;  would be a contradiction), so that
would be a contradiction), so that  and
and  such that
such that  which are the best proximity points and also fixed points.
which are the best proximity points and also fixed points.
If  , then
, then  for some
for some  which is not obviously a fixed point, since
which is not obviously a fixed point, since  , so that
, so that

for some  defined by
defined by  . Furthermore,
. Furthermore,  since
since  (resp.,
(resp.,  ), what yields
), what yields  (resp.,
(resp.,  );
);  and
and  since
since  .
.
Definition 2.9.
A 2-cyclic  -Kannan self-mapping
-Kannan self-mapping  defined for some real
defined for some real  and some
and some  (see Definitions 2.1 and 2.7) is of Meir-Keeler type if for any given
(see Definitions 2.1 and 2.7) is of Meir-Keeler type if for any given  ,
,  such that (2.8) holds.
such that (2.8) holds.
Proposition 2.3, Definitions 2.1 and 2.9, and Proposition 2.8 yield directly the following result.
Proposition 2.10.
Assume that  is a 2-cyclic contraction self-mapping of Meir- Keeler type with
is a 2-cyclic contraction self-mapping of Meir- Keeler type with  . Then,
. Then,  is also a 2-cyclic
is also a 2-cyclic  -Kannan self-mapping,
-Kannan self-mapping,  . If
. If  , then
, then  .
.
From the definition of  -contraction self-mappings and Definition 2.7 for Meir-Keeler type contraction self-mappings, the following result holds.
-contraction self-mappings and Definition 2.7 for Meir-Keeler type contraction self-mappings, the following result holds.
Proposition 2.11.
If  is a
is a  -contraction self-mapping of Meir-Keeler type, then for any given
-contraction self-mapping of Meir-Keeler type, then for any given  ,
,  and
and  such that
such that

Proof.
Since  is a contraction self-mapping which is also of Meir-Keeler type, the result follows directly by combining (1.1) and (2.8).
is a contraction self-mapping which is also of Meir-Keeler type, the result follows directly by combining (1.1) and (2.8).
3.  -Cyclic
-Cyclic  -Contraction, Contractions of Meir-Keeler Type,
-Contraction, Contractions of Meir-Keeler Type,  -Cyclic
-Cyclic  -Kannan Self-Mappings, and Some Mutual Relationships
-Kannan Self-Mappings, and Some Mutual Relationships
A set of relevant results for  -cyclic self-mappings for
-cyclic self-mappings for  are obtained in [12]. Those self-mappings obey the subsequent definitions.
are obtained in [12]. Those self-mappings obey the subsequent definitions.
Definition 3.1 (see [12]).
Let  be nonempty subsets of a metric space
be nonempty subsets of a metric space  ;
;  . Then,
. Then,  is a
is a  -cyclic self-mapping if
-cyclic self-mapping if  ;
;  with
with  ;
;  .
.
Definition 3.2.
Let  be nonempty,
be nonempty,  subsets of a metric space
subsets of a metric space  . Then,
. Then,  is a
is a  -cyclic
-cyclic  -contraction self-mapping if
-contraction self-mapping if  ;
;  with
with  ;
;  and, furthermore,
and, furthermore,

for some real constant  .
.
A point  is said to be the best proximity point if
is said to be the best proximity point if  , [12]. In this paper, it is also proven that if
, [12]. In this paper, it is also proven that if  is a
is a  -cyclic nonexpansive self-mapping, that is,
-cyclic nonexpansive self-mapping, that is,  ;
;  ;
;  , then
, then  ;
;  (i.e., the distances between adjacent sets are identical). Some properties concerned with
(i.e., the distances between adjacent sets are identical). Some properties concerned with  -cyclic nonexpansive self-mappings are stated and proven in the next lemma.
-cyclic nonexpansive self-mappings are stated and proven in the next lemma.
Lemma 3.3.
The following properties hold:
-
(i)
let
 be a
be a  -cyclic
-cyclic 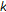 -contraction self-mapping, then,
-contraction self-mapping, then,  (3.2)
(3.2)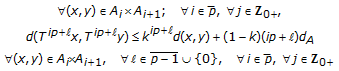 (3.3)
(3.3)where
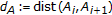 ;
; 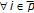 .
.Let the mappings
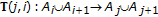 ;
;  ,
, 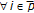 , be defined by
, be defined by (3.4)
(3.4)If
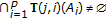 ;
; 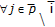 ,
, 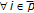 , with
, with 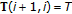 ;
; 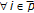 , there is
, there is  which is unique if
which is unique if  is complete.
is complete. -
(ii)
If
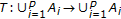 is a
is a  -cyclic nonexpansive self-mapping and, in particular, if t is a
-cyclic nonexpansive self-mapping and, in particular, if t is a  -cyclic
-cyclic  -contraction, then
-contraction, then  (3.5)
(3.5)
Proof.
-
(i)
Equation (3.2) follows by constructing a recursion directly from (1.1);
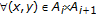 ;
;  ,
,  which can be also written equivalently in the form (3.3) by using the index identity
which can be also written equivalently in the form (3.3) by using the index identity 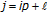 ;
; 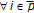 ,
, 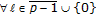 . If
. If 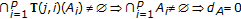 , then
, then  ;
;  ,
,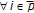 from (3.2) since
from (3.2) since 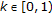 , so that there exists
, so that there exists 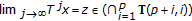 ;
;  . The point
. The point  is in
is in 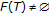 since
since 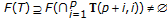 by construction of the self-mappings
by construction of the self-mappings 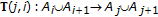 ;
; 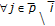 ,
, 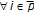 since
since 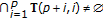 . Also,
. Also,  is unique if
is unique if 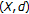 is complete. Property (i) has been proven.
is complete. Property (i) has been proven. -
(ii)
It follows from the recursion
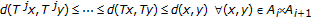 ;
; 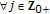 , obtained from (3.2) for
, obtained from (3.2) for 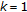 , since
, since  is nonexpansive.
is nonexpansive.
The auxiliary properties of Remark 3.4 below have been used in the proof of Lemma 3.3.
Remark 3.4.
Note that

so that

so that

The concepts of  -cyclic nonexpansive self-mapping and
-cyclic nonexpansive self-mapping and  -cyclic
-cyclic  -contraction are generalized in the following. Consider the mappings
-contraction are generalized in the following. Consider the mappings  with
with  ;
;  ,
,  ,
,  and
and  ;
;  which fulfil the constraint
which fulfil the constraint

for some  ;
;  and associated composed mappings
and associated composed mappings  defined by
defined by  ;
;  , subject to
, subject to  .
.
Remark 3.5.
Note that  is also defined for points
is also defined for points  for some nonempty indexing set
for some nonempty indexing set  , which contains
, which contains  , by restricting its domain and image as
, by restricting its domain and image as  for some nonempty indexing set
for some nonempty indexing set  such that
such that  (since
(since  ). An important observation is that a set of constraints of type (3.9) have to be satisfied if
). An important observation is that a set of constraints of type (3.9) have to be satisfied if 

The subsequent definitions extend Definitions 3.1-3.2 by removing the necessity of the set inclusions  ;
;  and allowing obtaining of contractions from the composed mappings
and allowing obtaining of contractions from the composed mappings  ;
;  which are not all necessarily contractions provided that
which are not all necessarily contractions provided that  ;
;  .
.
Definition 3.6.
Let  be nonempty subsets of a metric space with
be nonempty subsets of a metric space with  ,
,  . Then,
. Then,  ;
;  is a composed
is a composed  -cyclic self-mapping if
-cyclic self-mapping if  ;
;  with
with  ;
;  .
.
Definition 3.7.
Let  be nonempty subsets of a metric space
be nonempty subsets of a metric space  with
with  ,
,  . Then,
. Then,  ;
;  is a composed
is a composed  -cyclic
-cyclic  -contraction self-mapping if
-contraction self-mapping if  satisfies (3.9), subject to
satisfies (3.9), subject to  ,
,  ,
,  , and, furthermore,
, and, furthermore,

for some real constant  and, furthermore, if
and, furthermore, if  ;
;  with
with  ;
;  .
.
Definition 3.8.
If  fulfils Definition 3.7 with (3.11) being true also for
fulfils Definition 3.7 with (3.11) being true also for  , then it is said to be a composed
, then it is said to be a composed  -cyclic nonexpansive mapping.
-cyclic nonexpansive mapping.
Note that if  is a composed
is a composed  -cyclic nonexpansive self-mapping (resp., a composed
-cyclic nonexpansive self-mapping (resp., a composed  -cyclic
-cyclic  -contraction self-mapping) for some
-contraction self-mapping) for some  then it is so for all
then it is so for all  . Composed
. Composed  -cyclic contractions are characterized according to tests stated and proven in the subsequent result.
-cyclic contractions are characterized according to tests stated and proven in the subsequent result.
Proposition 3.9.
Assume that  are nonempty subsets of a metric space
are nonempty subsets of a metric space  ;
;  . Assume also that
. Assume also that  ;
;  ,
,  ;
;  and that
and that  ;
;  fulfils (3.9) for some
fulfils (3.9) for some  ;
;  .
.
Then, the self-mapping  ;
;  is a composed
is a composed  -cyclic
-cyclic  -contraction self-mapping if the following two conditions hold:
-contraction self-mapping if the following two conditions hold:


or  , otherwise.
, otherwise.
If  and
and  , then
, then  ;
;  is a composed
is a composed  -cyclic
-cyclic  -contraction self-mapping.
-contraction self-mapping.
Proof.
If  ;
;  fulfils (3.9), then for any
fulfils (3.9), then for any 

since  ;
;  ;
;  . Then,
. Then,  is a composed
is a composed  -cyclic
-cyclic  -contraction self-mapping from (3.12) and (3.11) (see Definition 3.7) if
-contraction self-mapping from (3.12) and (3.11) (see Definition 3.7) if

since  ;
;  . The second inequality of (3.13) is equivalent to
. The second inequality of (3.13) is equivalent to


Again since  ;
;  and since
and since  ;
;  , then
, then  , and
, and

Then (3.15) and (3.14), are equivalent to

The first part of the result has been proven since (3.11) holds. The second one is a direct conclusion of the first one for the case  .
.
It is now proven that if  and
and  ;
;  , then all the self-mappings
, then all the self-mappings  ;
;  are composed
are composed  -cyclic
-cyclic  -contraction self-mappings possessing fixed points. If, furthermore,
-contraction self-mappings possessing fixed points. If, furthermore,  is a complete metric space, then each of those self-mappings possesses a unique fixed point.
is a complete metric space, then each of those self-mappings possesses a unique fixed point.
Corollary 3.10.
Assume that  are nonempty subsets of a metric space
are nonempty subsets of a metric space  ;
;  and the composed
and the composed  -cyclic
-cyclic  -contraction self-mapping
-contraction self-mapping  fulfils Proposition 3.9 for some
fulfils Proposition 3.9 for some  , subject to
, subject to  ;
;  ,
,  ;
;  . Then, the following properties hold provided that
. Then, the following properties hold provided that  ;
;  .
.
-
(i)
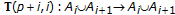 ;
; 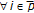 are all composed
are all composed  -cyclic
-cyclic 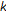 -contraction self-mappings which satisfy, in addition,
-contraction self-mappings which satisfy, in addition, 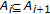 ;
;  (i.e.,
(i.e., 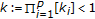 and
and 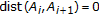 ;
; 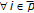 ) and which possess common fixed points in
) and which possess common fixed points in  , that is,
, that is, 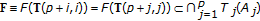 ;
;  .
. -
(ii)
There is a unique set
 satisfying the constraints
satisfying the constraints  , subject to
, subject to 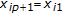 , for any given
, for any given 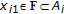 and for any given
and for any given 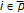 . Furthermore, each of those sets satisfies the limiting property
. Furthermore, each of those sets satisfies the limiting property  ;
;  for each
for each 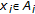 and any given
and any given  .
. -
(iii)
 consists of a unique point z if
consists of a unique point z if  is a complete metric space.
is a complete metric space. -
(iv)
If
 is a complete metric space, then there is a unique set
is a complete metric space, then there is a unique set 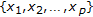 satisfying
satisfying 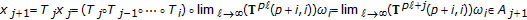 ;
; 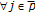 with
with  for any
for any  and any given
and any given 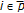 .
.
Proof.
-
(i)
If
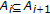 ;
; 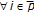 , then
, then 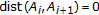 and
and  . From Proposition 3.9, constraint (3.11) holds with
. From Proposition 3.9, constraint (3.11) holds with 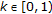 and
and 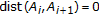 ;
; 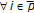 so that the limit
so that the limit 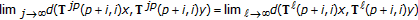 exists and is equal to zero;
exists and is equal to zero; 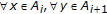 ,
,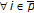 . Then,
. Then, 
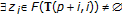 ;
;  since
since 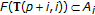 ,
,  ;
; 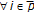 .
.If
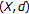 is complete, then
is complete, then 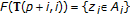 since the fixed point is unique. It is now proven by contradiction that
since the fixed point is unique. It is now proven by contradiction that 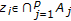 ;
; 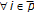 . Assume that
. Assume that 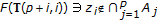 so that
so that 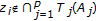 since
since 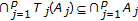 . Then,
. Then, 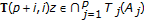 ;
; 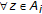 from the definition of the composed self-mapping
from the definition of the composed self-mapping  as
as 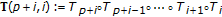 ;
; 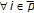 .
.As a result,
 which is a contradiction to the above assumption and proves the result. Now, it is proven that
which is a contradiction to the above assumption and proves the result. Now, it is proven that 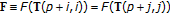 ;
; 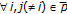 . Proceed by contradiction. Assume that
. Proceed by contradiction. Assume that 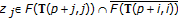 for some
for some 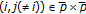 . Note that
. Note that 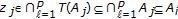 for the given
for the given 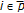 since
since 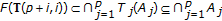 . Thus,
. Thus, 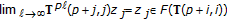 since
since 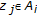 which contradicts
which contradicts  . Then,
. Then, 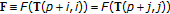 . Property (i) has been proven.
. Property (i) has been proven. -
(ii)
Let
 be a fixed point of
be a fixed point of 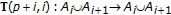 for any
for any 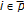 . A sequence
. A sequence  ;
;  ,
,  of
of  points exists obeying the iteration
points exists obeying the iteration  (3.18)
(3.18)
for some  for any
for any  ;
;  subject to
subject to  , since
, since

Then, the  -tuple
-tuple  , and thus the corresponding set
, and thus the corresponding set  is unique for each
is unique for each  and some
and some  since
since  is a self-mapping on
is a self-mapping on  ;
;  . On the other hand, there exists
. On the other hand, there exists  such that
such that  for each
for each  and each
and each  . Thus, a unique
. Thus, a unique  -tuple
-tuple  exists for each
exists for each  and then a unique set
and then a unique set  ;
;  . Property (ii) has been proven. Property (iii) follows directly from Property (i) together with Property (ii) since
. Property (ii) has been proven. Property (iii) follows directly from Property (i) together with Property (ii) since  is complete. Property (iv) follows directly from Properties (ii) and (iii).
is complete. Property (iv) follows directly from Properties (ii) and (iii).
Note that only a point in the unique set  , referred to in Corollary 3.10(iv), is a fixed point of the composed
, referred to in Corollary 3.10(iv), is a fixed point of the composed  -cyclic
-cyclic  -contraction self-mappings
-contraction self-mappings  on
on  ,
,  if the metric space
if the metric space  is complete. Also, there is only a guaranteed fixed point of the composed
is complete. Also, there is only a guaranteed fixed point of the composed  -cyclic
-cyclic  -contraction self-mappings
-contraction self-mappings  on
on  ;
;  , referred to in Corollary 3.10(ii), in each of the corresponding unique sets
, referred to in Corollary 3.10(ii), in each of the corresponding unique sets  if
if  is not complete.
is not complete.
An extra conclusion result can be obtained from Corollary 3.10 as follows in view of Remark 3.5:
Corollary 3.11.
The images of the mappings  are in
are in  ;
;  ,
,  . If, furthermore,
. If, furthermore,  and
and  ;
;  , then the image of
, then the image of  is in
is in  as
as  ;
;  . Also,
. Also,

Now, the self-mapping  is defined as
is defined as  for each
for each  such that
such that  for some
for some  ;
;  such that
such that  . It turns out that such a mapping is a
. It turns out that such a mapping is a  -cyclic
-cyclic  -contraction if the composed self-mappings
-contraction if the composed self-mappings  on
on  are composed
are composed  -cyclic
-cyclic  -contractions. Note that there always exists a unique
-contractions. Note that there always exists a unique  for each given
for each given  which, in addition, fulfils
which, in addition, fulfils  since
since  ;
;  . The following result is obtained directly from Corollaries 3.10(i) and 3.10(iv).
. The following result is obtained directly from Corollaries 3.10(i) and 3.10(iv).
Corollary 3.12.
Consider the self-mapping  , subject to
, subject to  ;
;  ,
,  , and assume that
, and assume that  and
and  ;
;  so that
so that  is a
is a  -cyclic
-cyclic  -contraction. Then,
-contraction. Then,  which, furthermore, consists of a single point if
which, furthermore, consists of a single point if  is a complete metric space.
is a complete metric space.
The relation between composed  -cyclic
-cyclic  -contractions satisfying Corollaries 3.10–3.12 and the so-called
-contractions satisfying Corollaries 3.10–3.12 and the so-called  -cyclic
-cyclic  -Kannan self-mappings defined below is now discussed. Let
-Kannan self-mappings defined below is now discussed. Let  be nonempty subsets of a metric space
be nonempty subsets of a metric space  ;
;  . Consider the mappings
. Consider the mappings  satisfying
satisfying  for
for  ;
;  for the nonempty subsets
for the nonempty subsets  of the metric space
of the metric space  . Note that this implies that
. Note that this implies that  ,
, , and
, and  . The following definition which generalizes Definition 2.1 is then used to prove further results.
. The following definition which generalizes Definition 2.1 is then used to prove further results.
Definition 3.13.
A self-mapping  is a composed
is a composed  -cyclic
-cyclic  -Kannan self-mapping if it satisfies the following property for some real
-Kannan self-mapping if it satisfies the following property for some real  and some
and some  :
:

Proposition 3.14.
Consider the self-mappings  with
with  for
for  ,
, ;
;  being composed
being composed  -cyclic
-cyclic  -contractions satisfying
-contractions satisfying  . The following properties hold.
. The following properties hold.
(i)The self-mappings  ;
;  and
and  are
are  self-mappings with
self-mappings with  .
.
(ii)The self-mappings  and
and  are, respectively,
are, respectively,  -cyclic
-cyclic  -Kannan self-mappings for all
-Kannan self-mappings for all  and composed
and composed  -cyclic
-cyclic  -Kannan self-mappings for some real constant
-Kannan self-mappings for some real constant  and any
and any  .
.
Proof.
(i) From (3.12) and the triangle inequality of the distance mapping

for a given  and
and  since
since  ;
;  . Since
. Since  ,
,

with  since
since  so that
so that  is a
is a  -Kannan self-mapping
-Kannan self-mapping  from (2.1) and so it is
from (2.1) and so it is  by construction. Property (i) has been proven. (ii) The proof follows directly since
by construction. Property (i) has been proven. (ii) The proof follows directly since  ;
;  so that (3.23) implies that (3.21) holds.
so that (3.23) implies that (3.21) holds.
Remark 3.15.
It turns out that Proposition 3.14(ii) which is slightly modified still holds if the inclusion conditions  ;
;  are removed. In fact, the self-mappings
are removed. In fact, the self-mappings  and
and  on
on  and on
and on  , respectively, are
, respectively, are  -cyclic
-cyclic  -Kannan self-mappings;
-Kannan self-mappings;  and composed
and composed  -cyclic
-cyclic  -Kannan self-mappings, respectively, for some real constant
-Kannan self-mappings, respectively, for some real constant  and
and  . The proof follows directly from that of Proposition 3.14(ii) and Definition 3.13 (see, in particular, (3.21)).
. The proof follows directly from that of Proposition 3.14(ii) and Definition 3.13 (see, in particular, (3.21)).
Definition 2.7 is generalized as follows for the case  , and the subsequent theorem compares
, and the subsequent theorem compares  -cyclic
-cyclic  -contractions with those of Meir-Keeler type.
-contractions with those of Meir-Keeler type.
Definition 3.16 (see [12]).
Assume that  are nonempty subsets of a metric space
are nonempty subsets of a metric space  with
with  . A
. A  -cyclic self-mapping
-cyclic self-mapping  is a contraction of Meir-Keeler type if for any given
is a contraction of Meir-Keeler type if for any given  ,
,  such that
such that

Note that the equivalent contrapositive logic proposition to (3.24) is

which can be used equivalently to state Definition 3.16. The following technical simple result will be then used in the proof of Theorem 3.18 below.
Assertion 1.
If (3.24), and equivalently (3.25), holds for some  , for any given
, for any given  , then they also hold for some
, then they also hold for some  .
.
Proof.
If  for the given
for the given  , the result is proven. If
, the result is proven. If  , then (3.25) leads directly to the property
, then (3.25) leads directly to the property

for any  ;
;  ,
, , and the result holds with the replacement
, and the result holds with the replacement  .
.
Proposition 3.17.
Let  be a
be a  -cyclic self-mapping on
-cyclic self-mapping on  . Thus, if
. Thus, if  is a
is a  -cyclic
-cyclic  -contraction, then it is also a contraction of Meir-Keeler type
-contraction, then it is also a contraction of Meir-Keeler type

Proof.
Since  is a
is a  -cyclic
-cyclic  -contraction, then it is
-contraction, then it is  -cyclic nonexpansive so that
-cyclic nonexpansive so that  ;
;  . Take any
. Take any  for some
for some  such that
such that  . Then, since
. Then, since  is a
is a  -cyclic
-cyclic  -contraction, one gets that
-contraction, one gets that

provided that for any given  ,
,  since
since  . Then, the
. Then, the  -cyclic self-mapping
-cyclic self-mapping  on
on  is also a contraction of Meir-Keeler type from Definition 3.16.
is also a contraction of Meir-Keeler type from Definition 3.16.
The subsequent result relies on the limiting property to the best proximity points of the distances between points in adjacent sets in self-mappings being  -cyclic contractions of Meir-Keeler type.
-cyclic contractions of Meir-Keeler type.
Theorem 3.18.
Let  be a
be a  -cyclic contraction of Meir-Keeler type. Then the following properties hold.
-cyclic contraction of Meir-Keeler type. Then the following properties hold.
(i)If  for some real constants
for some real constants  then the inequalities
then the inequalities  hold for some bounded positive strictly monotone decreasing real sequences
hold for some bounded positive strictly monotone decreasing real sequences  ,
,  which converge to zero, with
which converge to zero, with  ,
,  , and furthermore,
, and furthermore,  as
as  ;
;  ,
,  , where
, where

for  . As a result, there exists a finite
. As a result, there exists a finite  such that
such that

for any given  and
and  .
.
(ii)If  , then
, then  ;
;  , and
, and  consists of a unique fixed point if
consists of a unique fixed point if  is complete.
is complete.
(iii)There exists some real constant  such that
such that

and, furthermore,  under the constraint
under the constraint  which allows the choice
which allows the choice  ;
;  .
.
Proof.
( )-(
)-( ) A recursion in (3.24) leads to the following recursion of implications for
) A recursion in (3.24) leads to the following recursion of implications for  :
:

for  for any arbitrary given
for any arbitrary given  and some positive real sequences
and some positive real sequences  and
and  which depend on
which depend on  according to the respective implicit dependences:
according to the respective implicit dependences:

with  ,
,  which satisfy the constraints
which satisfy the constraints

which imply that

Furthermore, from (3.35) into (3.32), it follows that

so that

for some  , which does not depend neither on the particular initial pair
, which does not depend neither on the particular initial pair  ,
, nor on the given arbitrary
nor on the given arbitrary  since it is the supremum of all the limit superiors. Assume that
since it is the supremum of all the limit superiors. Assume that  . Since
. Since  is arbitrary, it may be chosen as
is arbitrary, it may be chosen as  which contradicts
which contradicts  . Then,
. Then, 

Also, since

for  . If
. If  , then
, then  ;
;  so that
so that  ,
,  ,
, , and since
, and since  from
from  ;
;  , then
, then  ;
;  . This conclusion is direct from the following reasoning. Assume that
. This conclusion is direct from the following reasoning. Assume that  for some arbitrary
for some arbitrary  which exists since
which exists since  is a fixed point. Then,
is a fixed point. Then,  for any
for any  with
with  ;
;  . Thus,
. Thus,  . Also,
. Also,  consists of a unique fixed point if
consists of a unique fixed point if  is complete. Properties (i) and (ii) have been proven.
is complete. Properties (i) and (ii) have been proven.
It turns out from (3.35) that for some finite  ,
,  ;
;  . Then, by construction, it follows that there exist some real constant
. Then, by construction, it follows that there exist some real constant  and some real constant
and some real constant  (both of them are dependent on
(both of them are dependent on  and
and  ) which are the respective ratios of the geometric series
) which are the respective ratios of the geometric series  and
and  , such that the following identities hold for any given sequence
, such that the following identities hold for any given sequence  that satisfies (3.35):
that satisfies (3.35):

If  , then a sequence satisfying
, then a sequence satisfying  ;
;  is valid from Assertion 1. Thus,
is valid from Assertion 1. Thus,  , and since
, and since  may be always taken as on being larger than
may be always taken as on being larger than  , then
, then

and together with (3.38), it follows that  ;
;  since
since

under the constraints  and
and  ;
;  . Property (iii) has been proven.
. Property (iii) has been proven.
It is interesting to discuss when the composed self-mappings  on
on  for set-depending self-mappings
for set-depending self-mappings  ;
;  as well as the self-mappings
as well as the self-mappings  on
on  defined by
defined by  are guaranteed to be
are guaranteed to be  -cyclic Meir-Keeler contractions without requiring that the property holds for each individual
-cyclic Meir-Keeler contractions without requiring that the property holds for each individual  subject to
subject to  . For the related discussion, assume that
. For the related discussion, assume that  ;
;  ,
,  for a set of real constants
for a set of real constants  ;
;  . A direct calculation on
. A direct calculation on  iterations yields directly
iterations yields directly

If the self-mappings  are identical;
are identical;  , then (3.43) becomes in particular:
, then (3.43) becomes in particular:

The following result holds directly from (3.43) and (3.44) and Theorem 3.18.
Theorem 3.19.
The composed self-mappings  on
on  for set- depending self-mappings
for set- depending self-mappings  ;
;  as well as the self-mappings T on
as well as the self-mappings T on  defined by
defined by  are guaranteed to be as follows.
are guaranteed to be as follows.
 -cyclic Meir-Keeler contractions if
-cyclic Meir-Keeler contractions if  ,
,
Thus, there is an asymptotic convergence from any initial point to the best proximity point in general and to a fixed point if the sets in have a nonempty intersection. The fixed point is unique if
have a nonempty intersection. The fixed point is unique if is complete.
is complete.
Nonexpansive  -cyclic self-mappings if
-cyclic self-mappings if  .
.
Expansive  -cyclic self-mappings if
-cyclic self-mappings if  .
.
More general conditions than the Meir-Keeler ones guaranteeing that the composed self-mappings  on
on  ,
,  are asymptotic contractions are now discussed.
are asymptotic contractions are now discussed.
Theorem 3.20.
Assume that there is a real sequence  of finite sum
of finite sum  which satisfies the conditions
which satisfies the conditions

for some given real constant  , whose elements are defined in such a way that the composed self-mapping
, whose elements are defined in such a way that the composed self-mapping  on satisfies
on satisfies

Then,  ;
;  .
.
Proof.
From the properties of the sequence and (3.46), one gets
sequence and (3.46), one gets

for some sufficiently large finite  .The constraint on the upperbounds in (3.47) guarantees that the strict upper-bound
.The constraint on the upperbounds in (3.47) guarantees that the strict upper-bound  for
for  is less than a strict upper-bound for
is less than a strict upper-bound for  for any sufficiently large
for any sufficiently large  provided that
provided that

Furthermore, (3.46) holds  if
if  ;
;  . As a result,
. As a result,  as
as  since the supremum of all limits superior converge to
since the supremum of all limits superior converge to  (see the proof of Theorem 3.19).
(see the proof of Theorem 3.19).
Theorem 3.20 may be particularized to  -cyclic asymptotic contractions as follows.
-cyclic asymptotic contractions as follows.
Theorem 3.21.
Assume that there is a real sequence  of finite sum
of finite sum  which satisfies the following conditions for some
which satisfies the following conditions for some  :
:

for some given real constant  whose elements are defined in such a way that the composed self-mapping satisfies
whose elements are defined in such a way that the composed self-mapping satisfies

Then,  for the given
for the given  .
.
Proof.
From the properties of the  sequence and (3.50), one gets.
sequence and (3.50), one gets.

for some sufficiently large finite  and the given
and the given  . The constraint on the upper-bounds in (3.51) guarantees that the strict upper-bound
. The constraint on the upper-bounds in (3.51) guarantees that the strict upper-bound  for
for  is less than a strict upper-bound for
is less than a strict upper-bound for  for any sufficiently large
for any sufficiently large  provided that
provided that

Furthermore, (3.50) holds  for the given
for the given  if
if  ;
;  for the given
for the given  . As a result,
. As a result,  as
as  since the supremum of all limit superiors converges to
since the supremum of all limit superiors converges to  (see the proof of Theorem 3.19).
(see the proof of Theorem 3.19).
Note that Theorem 3.21 guarantees that the self-mapping  on
on  has a
has a  -cyclic Meir-Keeler asymptotic contraction for a particular
-cyclic Meir-Keeler asymptotic contraction for a particular  , while Theorem 3.20 guarantees that all the self-mappings
, while Theorem 3.20 guarantees that all the self-mappings  are asymptotic contractions. In both cases, the self-mappings can be locally expansive in the sense that it can happen that
are asymptotic contractions. In both cases, the self-mappings can be locally expansive in the sense that it can happen that  for some finite
for some finite  , some
, some  , and some
, and some  .
.
References
Dominguez Benavides T, Phothi S: The fixed point property under renorming in some classes of Banach spaces. Nonlinear Analysis: Theory, Methods &Applications 2010,72(3–4):1409–1416. 10.1016/j.na.2009.08.024
Suzuki T: A new type of fixed point theorem in metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(11):5313–5317. 10.1016/j.na.2009.04.017
Burgić Dž, Kalabušić S, Kulenović MRS: Global attractivity results for mixed-monotone mappings in partially ordered complete metric spaces. Fixed Point Theory and Applications 2009, 2009:-17.
Nieto JJ, Pouso RL, Rodríguez-López R: Fixed point theorems in ordered abstract spaces. Proceedings of the American Mathematical Society 2007,135(8):2505–2517. 10.1090/S0002-9939-07-08729-1
Olatinwo MO: Some common fixed point theorems for selfmappings satisfying two contractive conditions of integral type in a uniform space. Central European Journal of Mathematics 2008,6(2):335–341. 10.2478/s11533-008-0023-y
Azhmyakov V: Convexity of the set of fixed points generated by some control systems. Journal of Applied Mathematics 2009, 2009:-14.
De la Sen M: Total stability properties based on fixed point theory for a class of hybrid dynamic systems. Fixed Point Theory and Applications 2009, 2009:-19.
De la Sen M: About robust stability of dynamic systems with time delays through fixed point theory. Fixed Point Theory and Applications 2008, 2008:-20.
De la Sen M: Quadratic stability and stabilization of switched dynamic systems with uncommensurate internal point delays. Applied Mathematics and Computation 2007,185(1):508–526. 10.1016/j.amc.2006.07.048
De la Sen M: On the robust adaptive stabilization of a class of nominally first-order hybrid systems. IEEE Transactions on Automatic Control 1999,44(3):597–602. 10.1109/9.751359
Meir A, Keeler E: A theorem on contraction mappings. Journal of Mathematical Analysis and Applications 1969,28(2):326–329. 10.1016/0022-247X(69)90031-6
Karpagam S, Agrawal S: Best proximity point theorems for
 -cyclic Meir-Keeler contractions. Fixed Point Theory and Applications 2009, 2009:-9.
-cyclic Meir-Keeler contractions. Fixed Point Theory and Applications 2009, 2009:-9.Chen C-M, Chang T-H: Fixed point theorems for a weaker Meir-Keeler type
 -set contraction in metric spaces. Fixed Point Theory and Applications 2009, 2009:-8.
-set contraction in metric spaces. Fixed Point Theory and Applications 2009, 2009:-8.Eldred AA, Veeramani P: Existence and convergence of best proximity points. Journal of Mathematical Analysis and Applications 2006,323(2):1001–1006. 10.1016/j.jmaa.2005.10.081
Kikkawa M, Suzuki T: Some similarity between contractions and Kannan mappings. Fixed Point Theory and Applications 2008, 2008:-8.
Enjouji Y, Nakanishi M, Suzuki T: A generalization of Kannan's fixed point theorem. Fixed Point Theory and Applications 2009, 2009:-10.
De la Sen M: Some combined relations between contractive mappings, Kannan mappings, reasonable expansive mappings, and
 -stability. Fixed Point Theory and Applications 2009, 2009:-25.
-stability. Fixed Point Theory and Applications 2009, 2009:-25.Inoue G, Takahashi W, Zembayashi K: Strong convergence theorems by hybrid methods for maximal monotone operators and relatively nonexpansive mappings in Banach spaces. Journal of Convex Analysis 2009,16(3–4):791–806.
Aoyama K, Kohsaka F, Takahashi W: Strongly relatively nonexpansive sequences in Banach spaces and applications. Journal of Fixed Point Theory and Applications 2009,5(2):201–225. 10.1007/s11784-009-0108-7
Chen C, Zhu C: Fixed point theorems for
 times reasonable expansive mapping. Fixed Point Theory and Applications 2008, 2008:-6.
times reasonable expansive mapping. Fixed Point Theory and Applications 2008, 2008:-6.
Acknowledgments
The author is grateful to the Spanish Ministry of Education for its partial support to this work through Grant DPI 2009-07197. He is also grateful to the Basque Government for its support through Grants GIC07143-IT-269-07and SAIOTEK S-PE07UN04. The author thanks the reviewers for their useful comments who helped him to improve the former versions of the manuscript.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
De la Sen, M. Linking Contractive Self-Mappings and Cyclic Meir-Keeler Contractions with Kannan Self-Mappings. Fixed Point Theory Appl 2010, 572057 (2010). https://doi.org/10.1155/2010/572057
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/572057
 -Contraction, 2-Cyclic
-Contraction, 2-Cyclic  -Kannan Self-Mappings, Contractions of Meir-Keeler Type, and Some Mutual Relationships
-Kannan Self-Mappings, Contractions of Meir-Keeler Type, and Some Mutual Relationships -Cyclic
-Cyclic  -Contraction, Contractions of Meir-Keeler Type,
-Contraction, Contractions of Meir-Keeler Type,  -Cyclic
-Cyclic  -Kannan Self-Mappings, and Some Mutual Relationships
-Kannan Self-Mappings, and Some Mutual Relationships be a
be a  -cyclic
-cyclic 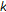 -contraction self-mapping, then,
-contraction self-mapping, then, 
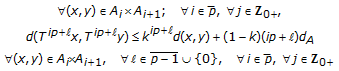
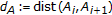 ;
; 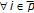 .
.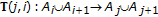 ;
;  ,
, 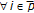 , be defined by
, be defined by
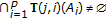 ;
; 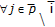 ,
, 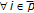 , with
, with 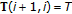 ;
; 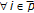 , there is
, there is  which is unique if
which is unique if  is complete.
is complete.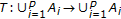 is a
is a  -cyclic nonexpansive self-mapping and, in particular, if t is a
-cyclic nonexpansive self-mapping and, in particular, if t is a  -cyclic
-cyclic  -contraction, then
-contraction, then 
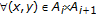 ;
;  ,
,  which can be also written equivalently in the form (3.3) by using the index identity
which can be also written equivalently in the form (3.3) by using the index identity 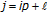 ;
; 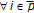 ,
, 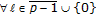 . If
. If 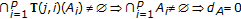 , then
, then  ;
;  ,
,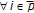 from (3.2) since
from (3.2) since 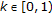 , so that there exists
, so that there exists 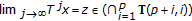 ;
;  . The point
. The point  is in
is in 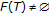 since
since 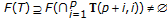 by construction of the self-mappings
by construction of the self-mappings 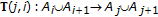 ;
; 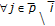 ,
, 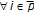 since
since 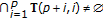 . Also,
. Also,  is unique if
is unique if 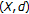 is complete. Property (i) has been proven.
is complete. Property (i) has been proven.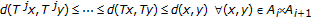 ;
; 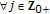 , obtained from (3.2) for
, obtained from (3.2) for 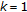 , since
, since  is nonexpansive.
is nonexpansive. ;
; 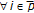 are all composed
are all composed  -cyclic
-cyclic 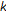 -contraction self-mappings which satisfy, in addition,
-contraction self-mappings which satisfy, in addition, 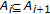 ;
;  (i.e.,
(i.e., 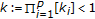 and
and 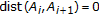 ;
; 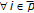 ) and which possess common fixed points in
) and which possess common fixed points in  , that is,
, that is, 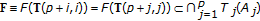 ;
;  .
. satisfying the constraints
satisfying the constraints  , subject to
, subject to 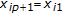 , for any given
, for any given 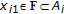 and for any given
and for any given 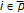 . Furthermore, each of those sets satisfies the limiting property
. Furthermore, each of those sets satisfies the limiting property  ;
;  for each
for each 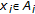 and any given
and any given  .
. consists of a unique point z if
consists of a unique point z if  is a complete metric space.
is a complete metric space. is a complete metric space, then there is a unique set
is a complete metric space, then there is a unique set 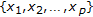 satisfying
satisfying 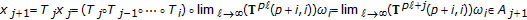 ;
; 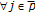 with
with  for any
for any  and any given
and any given 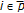 .
.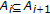 ;
; 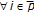 , then
, then 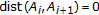 and
and  . From Proposition 3.9, constraint (3.11) holds with
. From Proposition 3.9, constraint (3.11) holds with 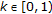 and
and 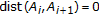 ;
; 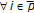 so that the limit
so that the limit 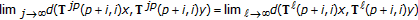 exists and is equal to zero;
exists and is equal to zero; 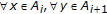 ,
,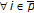 . Then,
. Then, 
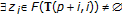 ;
;  since
since 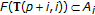 ,
,  ;
; 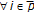 .
.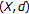 is complete, then
is complete, then 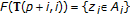 since the fixed point is unique. It is now proven by contradiction that
since the fixed point is unique. It is now proven by contradiction that 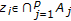 ;
; 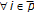 . Assume that
. Assume that 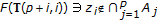 so that
so that 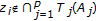 since
since 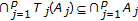 . Then,
. Then, 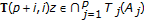 ;
; 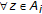 from the definition of the composed self-mapping
from the definition of the composed self-mapping  as
as 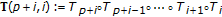 ;
; 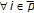 .
. which is a contradiction to the above assumption and proves the result. Now, it is proven that
which is a contradiction to the above assumption and proves the result. Now, it is proven that 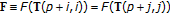 ;
; 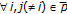 . Proceed by contradiction. Assume that
. Proceed by contradiction. Assume that 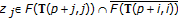 for some
for some 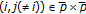 . Note that
. Note that 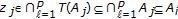 for the given
for the given 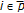 since
since 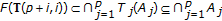 . Thus,
. Thus, 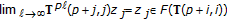 since
since 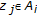 which contradicts
which contradicts  . Then,
. Then, 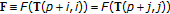 . Property (i) has been proven.
. Property (i) has been proven. be a fixed point of
be a fixed point of 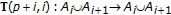 for any
for any 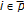 . A sequence
. A sequence  ;
;  ,
,  of
of  points exists obeying the iteration
points exists obeying the iteration 
 -cyclic Meir-Keeler contractions. Fixed Point Theory and Applications 2009, 2009:-9.
-cyclic Meir-Keeler contractions. Fixed Point Theory and Applications 2009, 2009:-9.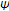 -set contraction in metric spaces. Fixed Point Theory and Applications 2009, 2009:-8.
-set contraction in metric spaces. Fixed Point Theory and Applications 2009, 2009:-8. -stability. Fixed Point Theory and Applications 2009, 2009:-25.
-stability. Fixed Point Theory and Applications 2009, 2009:-25. times reasonable expansive mapping. Fixed Point Theory and Applications 2008, 2008:-6.
times reasonable expansive mapping. Fixed Point Theory and Applications 2008, 2008:-6.