- Research Article
- Open access
- Published:
On Two Iterative Methods for Mixed Monotone Variational Inequalities
Fixed Point Theory and Applications volume 2010, Article number: 291851 (2009)
Abstract
A mixed monotone variational inequality (MMVI) problem in a Hilbert space  is formulated to find a point
is formulated to find a point  such that
such that  for all
for all  , where
, where  is a monotone operator and
is a monotone operator and  is a proper, convex, and lower semicontinuous function on
is a proper, convex, and lower semicontinuous function on  . Iterative algorithms are usually applied to find a solution of an MMVI problem. We show that the iterative algorithm introduced in the work of Wang et al., (2001) has in general weak convergence in an infinite-dimensional space, and the algorithm introduced in the paper of Noor (2001) fails in general to converge to a solution.
. Iterative algorithms are usually applied to find a solution of an MMVI problem. We show that the iterative algorithm introduced in the work of Wang et al., (2001) has in general weak convergence in an infinite-dimensional space, and the algorithm introduced in the paper of Noor (2001) fails in general to converge to a solution.
1. Introduction
Let  be a real Hilbert space with inner product
be a real Hilbert space with inner product  and norm
and norm  and let
and let  be an operator with domain
be an operator with domain  and range
and range  in
in  . Recall that
. Recall that  is monotone if its graph
is monotone if its graph  is a monotone set in
is a monotone set in  . This means that
. This means that  is monotone if and only if
is monotone if and only if

A monotone operator  is maximal monotone if its graph
is maximal monotone if its graph  is not properly contained in the graph of any other monotone operator on
is not properly contained in the graph of any other monotone operator on  .
.
Let 
 be a proper, convex, and lower semicontinuous functional. Thesubdifferential of
be a proper, convex, and lower semicontinuous functional. Thesubdifferential of 
 is defined by
is defined by

It is well known (cf. [1]) that  is a maximal monotone operator.
is a maximal monotone operator.
Themixed monotone variational inequality (MMVI) problem is to find a point  with the property
with the property

where  is a monotone operator and
is a monotone operator and  is a proper, convex, and lower semicontinuous function on
is a proper, convex, and lower semicontinuous function on  .
.
If one takes  to be the indicator of a closed convex subset
to be the indicator of a closed convex subset  of
of  ,
,

then the MMVI (1.3) is reduced to the classical variational inequality (VI):

Recall that theresolvent of a monotone operator  is defined as
is defined as

If  , we write
, we write  for
for  It is known that
It is known that  is monotone if and only of for each
is monotone if and only of for each  the resolvent
the resolvent  is nonexpansive, and
is nonexpansive, and  is maximal monotone if and only of for each
is maximal monotone if and only of for each  , the resolvent
, the resolvent  is nonexpansive and defined on the entire space
is nonexpansive and defined on the entire space  . Recall that a self-mapping of a closed convex subset
. Recall that a self-mapping of a closed convex subset  of
of  is said to be
is said to be
(i)nonexpansive if  for all
for all  ;
;
(ii)firmly nonexpansive if  for
for  . Equivalently,
. Equivalently,  is firmly nonexpansive if and only of
is firmly nonexpansive if and only of  is nonexpansive. It is known that each resolvent of a monotone operator is firmly nonexpansive.
is nonexpansive. It is known that each resolvent of a monotone operator is firmly nonexpansive.
We use  to denote the set of fixed points of
to denote the set of fixed points of  ; that is,
; that is,  .
.
Variational inequalities have extensively been studied; see the monographs by Baiocchi and Capelo [2], Cottle et al. [3], Glowinski et al. [4], Giannessi and Maugeri [5], and Kinderlehrer and Stampacciha [6].
Iterative methods play an important role in solving variational inequalities. For example, if  is a single-valued, strongly monotone (i.e.,
is a single-valued, strongly monotone (i.e.,  for all
for all  and some
and some  ), and Lipschitzian (i.e.,
), and Lipschitzian (i.e.,  for some
for some  and all
and all  ) operator on
) operator on  , then the sequence
, then the sequence  generated by the iterative algorithm
generated by the iterative algorithm

where  is the identity operator and
is the identity operator and  is the metric projection of
is the metric projection of  onto
onto  , and the initial guess
, and the initial guess  is chosen arbitrarily, converges strongly to the unique solution of VI (1.5) provided,
is chosen arbitrarily, converges strongly to the unique solution of VI (1.5) provided,  is small enough.
is small enough.
2. An Inexact Implicit Method
In this section we study the convergence of an inexact implicit method for solving the MMVI (1.3) introduced by Wang et al. [7] (see also [8, 9] for related work).
Let  and
and  be two sequences of nonnegative numbers such that
be two sequences of nonnegative numbers such that

Let  and
and  . The inexact implicit method introduced in [7] generates a sequence
. The inexact implicit method introduced in [7] generates a sequence  defined in the following way. Once
defined in the following way. Once  has been constructed, the next iterate
has been constructed, the next iterate  is implicitly constructed satisfying the equation
is implicitly constructed satisfying the equation

where  is a sequence of nonnegative numbers such that
is a sequence of nonnegative numbers such that

for  , and for
, and for  and
and  ,
,

and where  is such that
is such that

with  given as follows:
given as follows:

We note that  is a solution of the MMVI (1.3) if and only if, for each
is a solution of the MMVI (1.3) if and only if, for each  ,
,  satisfies the fixed point equation
satisfies the fixed point equation

Before discussing the convergence of the implicit algorithm (2.2), we look at a special case of (2.2), where  . In this case, the MMVI (1.3) reduces to the problem of finding a
. In this case, the MMVI (1.3) reduces to the problem of finding a  such that
such that

in another word, finding an absolute minimizer  of
of  over
over  . This is equivalent to solving the inclusion
. This is equivalent to solving the inclusion

and the algorithm (2.2) is thus reduced to a special case of the Eckastein-Bertsekas algorithm [10]

where  If
If  , then algorithm (2.2) is reduced to a special case of Rockafellar's proximal point algorithm [11]
, then algorithm (2.2) is reduced to a special case of Rockafellar's proximal point algorithm [11]

Rockafellar's proximal point algorithm for finding a zero of a maximal monotone operator has received tremendous investigations; see [12–14] and the references therein.
Remark 2.1.
Theorem 5.1 of Wang et al. [7] holds true only in the finite-dimensional setting. This is because in the infinite-dimensional setting, a bounded sequence fails, in general, to have a norm-convergent subsequence. As a matter of fact, in the infinite-dimensional case, the special case of (2.2) where  and
and  corresponds to Rockafellar's proximal point algorithm (2.11) which fails to converge in the norm topology, in general, in the infinite-dimensional setting; see Güler's counterexample [15]. This infinite-dimensionality problem occurred in several papers by Noor (see, e.g., [16–26]).
corresponds to Rockafellar's proximal point algorithm (2.11) which fails to converge in the norm topology, in general, in the infinite-dimensional setting; see Güler's counterexample [15]. This infinite-dimensionality problem occurred in several papers by Noor (see, e.g., [16–26]).
In the infinite-dimensional setting, whether or not Wang et al.'s implicit algorithm (2.2) converges even in the weak topology remains an open question. We will provide a partial answer by showing that if the operator  is weak-to-strong continuous (i.e.,
is weak-to-strong continuous (i.e.,  takes weakly convergent sequences to strongly convergent sequences), then the implicit algorithm (2.2) does converge weakly.
takes weakly convergent sequences to strongly convergent sequences), then the implicit algorithm (2.2) does converge weakly.
We next collect the (correct) results proved in [7].
Proposition 2.2.
Assume that  is generated by the implicit algorithm (2.2).
is generated by the implicit algorithm (2.2).
(a)For  ,
,  is a nondecreasing function of
is a nondecreasing function of  .
.
-
(b)
If
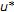 is a solution to the MMVI (1.3),
is a solution to the MMVI (1.3), 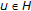 and
and 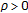 , then
, then  (2.12)
(2.12)
(c)For any solution  to the MMVI (1.3),
to the MMVI (1.3),

where  satisfies
satisfies  .
.
(d) is bounded.
is bounded.
(e)There is a  such that
such that 
Since algorithm (2.2) is, in general, not strongly convergent, we turn to investigate its weak convergence. It is however unclear if the algorithm is weakly convergent (if the space is infinite dimensional). We present a partial answer below. But first recall that an operator  is said to be weak-to-strong continuous if the weak convergence of a sequence
is said to be weak-to-strong continuous if the weak convergence of a sequence  to a point
to a point  implies the strong convergence of the sequence
implies the strong convergence of the sequence  to the point
to the point  .
.
Theorem 2.3.
Assume that  is generated by algorithm (2.2). If
is generated by algorithm (2.2). If  is weak-to-strong continuous, then
is weak-to-strong continuous, then  converges weakly to a solution of the MMVI (1.3).
converges weakly to a solution of the MMVI (1.3).
Proof.
Putting

we have

It follows that

This implies that

So, if  weakly (hence
weakly (hence  strongly since
strongly since  is weak-to-strong continuous), it follows that
is weak-to-strong continuous), it follows that

Thus,  is a solution.
is a solution.
To prove that the entire sequence of  is weakly convergent, assume that
is weakly convergent, assume that  weakly. All we have to prove is that
weakly. All we have to prove is that  . Passing through further subsequences if necessary, we may assume that
. Passing through further subsequences if necessary, we may assume that  and
and  both exist.
both exist.
For  , since
, since  strongly and since
strongly and since  and
and  are bounded, there exists an integer
are bounded, there exists an integer  such that, for
such that, for 

It follows that for  ,
,

This implies

However,

It follows that

Similarly, by repeating the argument above we obtain

Adding these inequalities, we get  .
.
3. A Counterexample
It is not hard to see that  solves MMVI (1.3) if and only of
solves MMVI (1.3) if and only of  solves the inclusion
solves the inclusion

which is in turn equivalent to the fixed point equation

where  is the resolvent of
is the resolvent of  defined by
defined by

Recall that if  is the indicator of a closed convex subset
is the indicator of a closed convex subset  of
of  ,
,

then MMVI (1.3) is reduced to the classical variational inequality (VI)

In [27], Noor introduced a new iterative algorithm [27, Algorithm 3.3, page 36] as follows. Given  , compute
, compute  by the iterative scheme
by the iterative scheme

where  and
and  are constant, and
are constant, and  is given by
is given by

Noor [27] proved a convergence result for his algorithm (3.6) as follows.
Theorem 3.1 (see [27, page 38]).
Let  be a finite-dimensional Hilbert space. Then the sequence
be a finite-dimensional Hilbert space. Then the sequence  generated by algorithm (3.6) converges to a solution of MMVI (1.3).
generated by algorithm (3.6) converges to a solution of MMVI (1.3).
We however found that the conclusion stated in the above theorem is incorrect. It is true that  solves MMVI (1.3) if and only if
solves MMVI (1.3) if and only if  solves the fixed point equation (3.2). The reason that led Noor to his mistake is his claim that
solves the fixed point equation (3.2). The reason that led Noor to his mistake is his claim that  solves MMVI (1.3) if and only if
solves MMVI (1.3) if and only if  solves the following iterated fixed point equation:
solves the following iterated fixed point equation:

As a matter of fact, the two fixed point equations (3.2) and (3.8) are not equivalent, as shown in the following counterexample which also shows that the convergence result of Noor [27] is incorrect.
Example 3.2.
Take  . Define
. Define  and
and  by
by

Notice that (Clarke [28])

It is easily seen that  is the unique solution to the MMVI
is the unique solution to the MMVI

Observe that equation  is equivalent to the fixed point equation
is equivalent to the fixed point equation

Now since  for all
for all  , we get that
, we get that  solves (3.12) if and only if
solves (3.12) if and only if

where

It follows from (3.13) that  . Hence
. Hence

But, since

we deduce that the solution set  of the fixed point equation (3.12) is given by
of the fixed point equation (3.12) is given by

(We therefore conclude that equation  is not equivalent to MMVI (1.3), as claimed by Noor [27].)
is not equivalent to MMVI (1.3), as claimed by Noor [27].)
Now take the initial guess  for
for  . Then
. Then  and we have that algorithm (3.6) generates a constant sequence
and we have that algorithm (3.6) generates a constant sequence  for all
for all  . However,
. However,  is not a solution of MMVI (3.11). This shows that algorithm (3.6) may generate a sequence that fails to converge to a solution of MMVI (1.3) and Noor's result in [27] is therefore false.
is not a solution of MMVI (3.11). This shows that algorithm (3.6) may generate a sequence that fails to converge to a solution of MMVI (1.3) and Noor's result in [27] is therefore false.
Remark 3.3.
Noor has repeated his above mistake in a number of his recent articles. A partial search found that articles [20, 21, 26, 29–32] contain the same error.
References
Brezis H: Operateurs Maximaux Monotones et Semi-Groups de Contraction dans les Espaces de Hilbert. North-Holland, Amsterdam, The Netherlands; 1973.
Baiocchi C, Capelo A: Variational and Quasivariational Inequalities: Applications to Free Boundary Problems, A Wiley-Interscience Publication. John Wiley & Sons, New York, NY, USA; 1984:ix+452.
Cottle RW, Giannessi F, Lions JL: Variational Inequalities and Complementarity Problems: Theory and Applications. John Wiley & Sons, New York, NY, USA; 1980.
Glowinski R, Lions J-L, Trémolières R: Numerical Analysis of Variational Inequalities, Studies in Mathematics and Its Applications. Volume 8. North-Holland, Amsterdam, The Netherlands; 1981:xxix+776.
Giannessi F, Maugeri A: Variational Inequalities and Network Equilibrium Problems. Plenum Press, New York, NY, USA; 1995.
Kinderlehrer D, Stampacchia G: An Introduction to Variational Inequalities and Their Applications, Pure and Applied Mathematics. Volume 88. Academic Press, New York, NY, USA; 1980:xiv+313.
Wang SL, Yang H, He B: Inexact implicit method with variable parameter for mixed monotone variational inequalities. Journal of Optimization Theory and Applications 2001,111(2):431–443. 10.1023/A:1011942620208
He B: Inexact implicit methods for monotone general variational inequalities. Mathematical Programming 1999,86(1):199–217. 10.1007/s101070050086
Han D, He B: A new accuracy criterion for approximate proximal point algorithms. Journal of Mathematical Analysis and Applications 2001,263(2):343–354. 10.1006/jmaa.2001.7535
Eckstein J, Bertsekas DP: On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators. Mathematical Programming 1992,55(3):293–318. 10.1007/BF01581204
Rockafellar RT: Monotone operators and the proximal point algorithm. SIAM Journal on Control and Optimization 1976,14(5):877–898. 10.1137/0314056
Solodov MV, Svaiter BF: Forcing strong convergence of proximal point iterations in a Hilbert space. Mathematical Programming, Series A 2000,87(1):189–202.
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002,66(1):240–256. 10.1112/S0024610702003332
Marino G, Xu H-K: Convergence of generalized proximal point algorithms. Communications on Pure and Applied Analysis 2004,3(4):791–808.
Güler O: On the convergence of the proximal point algorithm for convex minimization. SIAM Journal on Control and Optimization 1991,29(2):403–419. 10.1137/0329022
Noor MA: Monotone mixed variational inequalities. Applied Mathematics Letters 2001,14(2):231–236. 10.1016/S0893-9659(00)00141-5
Noor MA: An implicit method for mixed variational inequalities. Applied Mathematics Letters 1998,11(4):109–113. 10.1016/S0893-9659(98)00066-4
Noor MA: A modified projection method for monotone variational inequalities. Applied Mathematics Letters 1999,12(5):83–87. 10.1016/S0893-9659(99)00061-0
Noor MA: Some iterative techniques for general monotone variational inequalities. Optimization 1999,46(4):391–401. 10.1080/02331939908844464
Noor MA: Some algorithms for general monotone mixed variational inequalities. Mathematical and Computer Modelling 1999,29(7):1–9. 10.1016/S0895-7177(99)00058-8
Noor MA: Splitting algorithms for general pseudomonotone mixed variational inequalities. Journal of Global Optimization 2000,18(1):75–89. 10.1023/A:1008322118873
Noor MA: An iterative method for general mixed variational inequalities. Computers & Mathematics with Applications 2000,40(2–3):171–176. 10.1016/S0898-1221(00)00151-6
Noor MA: Splitting methods for pseudomonotone mixed variational inequalities. Journal of Mathematical Analysis and Applications 2000,246(1):174–188. 10.1006/jmaa.2000.6776
Noor MA: A class of new iterative methods for general mixed variational inequalities. Mathematical and Computer Modelling 2000,31(13):11–19. 10.1016/S0895-7177(00)00108-4
Noor MA: Solvability of multivalued general mixed variational inequalities. Journal of Mathematical Analysis and Applications 2001,261(1):390–402. 10.1006/jmaa.2001.7533
Noor MA, Al-Said EA: Wiener-Hopf equations technique for quasimonotone variational inequalities. Journal of Optimization Theory and Applications 1999,103(3):705–714. 10.1023/A:1021796326831
Noor MA: Iterative schemes for quasimonotone mixed variational inequalities. Optimization 2001,50(1–2):29–44. 10.1080/02331930108844552
Clarke FH: Optimization and Nonsmooth Analysis, Classics in Applied Mathematics. Volume 5. 2nd edition. SIAM, Philadelphia, Pa, USA; 1990:xii+308.
Noor MA: An extraresolvent method for monotone mixed variational inequalities. Mathematical and Computer Modelling 1999,29(3):95–100. 10.1016/S0895-7177(99)00033-3
Noor MA: A modified extragradient method for general monotone variational inequalities. Computers & Mathematics with Applications 1999,38(1):19–24. 10.1016/S0898-1221(99)00164-9
Noor MA: Projection type methods for general variational inequalities. Soochow Journal of Mathematics 2002,28(2):171–178.
Noor MA: Modified projection method for pseudomonotone variational inequalities. Applied Mathematics Letters 2002,15(3):315–320. 10.1016/S0893-9659(01)00137-9
Acknowledgments
The authors are grateful to the anonymous referees for their comments and suggestions which improved the presentation of this manuscript. This paper is dedicated to Professor Wataru Takahashi on the occasion of his retirement. The second author supported in part by NSC 97-2628-M-110-003-MY3, and by DGES MTM2006-13997-C02-01.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Lu, X., Xu, HK. & Yin, X. On Two Iterative Methods for Mixed Monotone Variational Inequalities. Fixed Point Theory Appl 2010, 291851 (2009). https://doi.org/10.1155/2010/291851
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2010/291851
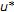 is a solution to the MMVI (1.3),
is a solution to the MMVI (1.3), 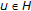 and
and 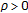 , then
, then 