- Research Article
- Open access
- Published:
Generalized Mann Iterations for Approximating Fixed Points of a Family of Hemicontractions
Fixed Point Theory and Applications volume 2008, Article number: 824607 (2008)
Abstract
This paper concerns common fixed points for a finite family of hemicontractions or a finite family of strict pseudocontractions on uniformly convex Banach spaces. By introducing a new iteration process with error term, we obtain sufficient and necessary conditions, as well as sufficient conditions, for the existence of a fixed point. As one will see, we derive these strong convergence theorems in uniformly convex Banach spaces and without any requirement of the compactness on the domain of the mapping. The results given in this paper extend some previous theorems.
1. Introduction
Let  be a real Banach space and
be a real Banach space and  a nonempty closed subset of
a nonempty closed subset of  . A mapping
. A mapping  is said to be pseudocontractive (see, e.g., [1]) if
is said to be pseudocontractive (see, e.g., [1]) if

holds for all  .
.  is said to be strictly pseudocontractive if, for all
is said to be strictly pseudocontractive if, for all  , there exists a constant
, there exists a constant  such that
such that

Denote by  the set of fixed points of
the set of fixed points of  . A map
. A map  is called hemicontractive if
is called hemicontractive if  and for all
and for all  ,
,  , the following inequality holds:
, the following inequality holds:

It is easy to see that the class of pseudocontractive mappings with fixed points is a subset of the class of hemicontractions.
There are many papers in the literature dealing with the approximation of fixed points for several classes of nonlinear mappings (see, e.g., [1–11], and the reference therein). In these works, there are two iterative methods to be used to find a point in  . One is explicit and one is implicit.
. One is explicit and one is implicit.
The explicit one is the following well-known Mann iteration.
Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of . For any
. For any  , the sequence
, the sequence  is defined by
is defined by

where  is a real sequence in
is a real sequence in  satisfying some assumptions.
satisfying some assumptions.
It has been applied to many classes of nonlinear mappings to find a fixed point. However, for hemicontractive mappings and strictly pseudocontractive mappings, the iteration process of convergence is in general not strong (see a counterexample given by Chidume and Mutangadura [3]). Most recently, Marino and Xu [6] proved that the Mann iterative sequence  converges weakly to a fixed point for strictly pseudocontractive mappings in a Hilbert space, while the real sequence
converges weakly to a fixed point for strictly pseudocontractive mappings in a Hilbert space, while the real sequence  satisfying (i)
satisfying (i)  and (ii)
and (ii)  .
.
In order to get strong convergence for fixed points of hemicontractive mappings and strictly pseudocontractive mappings, the following Mann-type implicit iteration scheme is introduced.
Let be a nonempty closed convex subset of
be a nonempty closed convex subset of with
with . For any
. For any , the sequence
, the sequence is generated by
is generated by

where is a real sequence in
is a real sequence in satisfying suitable conditions.
satisfying suitable conditions.
Recently, in the setting of a Hilbert space, Rafiq [12] proved that the Mann-type implicit iterative sequence  converges strongly to a fixed point for hemicontractive mappings, under the assumption that the domain
converges strongly to a fixed point for hemicontractive mappings, under the assumption that the domain  of
of  is a compact convex subset of a Hilbert space, and
is a compact convex subset of a Hilbert space, and  for some
for some  .
.
In this paper, we will study the strong convergence of the generalized Mann-type iteration scheme (see Definition 2.1) for hemicontractive and, respectively, pseudocontractive mappings. As we will see, our theorems extend the corresponding results in [12] in four aspects. (1) The space setting is a more general one: uniformly convex Banach space, which could not be a Hilbert space. (2) The requirement of the compactness on the domain of the mapping is dropped. (3) A single mapping is replaced by a family of mappings. (4) The Mann-type implicit iteration is replaced by the generalized Mann iteration. Moreover, we give answers to a question asked in [13].
2. Preliminaries and Lemmas
Definition 2.1 (generalized Mann iteration).
Let  be a fixed integer,
be a fixed integer,  , and
, and  a nonempty closed convex subset of
a nonempty closed convex subset of  satisfying the condition
satisfying the condition  . Let
. Let  be a family of mappings. For each
be a family of mappings. For each  , the sequence
, the sequence  is defined by
is defined by

where  ,
,  ,
,  and
and  are three sequences in
are three sequences in  with
with  and
and  is bounded.
is bounded.
The modulus of convexity of  is the function
is the function  defined by
defined by

 is called uniformly convex if and only if, for all
is called uniformly convex if and only if, for all  such that
such that  .
.  is called
is called  -uniformly convex if there exists a constant
-uniformly convex if there exists a constant  , such that
, such that  . It is well known (see [10]) that
. It is well known (see [10]) that

Let  be a Banach space,
be a Banach space,  and
and  . Then, we denote
. Then, we denote  .
.
Definition 2.2 (see [4]).
Let  be a nondecreasing function with
be a nondecreasing function with  and
and  , for all
, for all  .
.
-
(i)
A mapping
 with
with  is said to satisfy condition (A) on
is said to satisfy condition (A) on 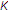 if there is a function
if there is a function 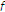 such that for all
such that for all  ,
, 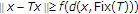 .
. -
(ii)
A finite family of mappings
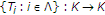 with
with 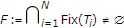 are said to satisfy condition (
are said to satisfy condition ( ) if there exists a function
) if there exists a function 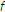 , such that
, such that 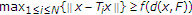 holds for all
holds for all  .
.
Lemma 2.3 (see [8]).
Let  be a real uniformly convex Banach space with the modulus of convexity of power type
be a real uniformly convex Banach space with the modulus of convexity of power type  . Then, for all
. Then, for all  in
in  and
and  , there exists a constant
, there exists a constant  such that
such that

where  .
.
Remark 2.4.
If  in the previous lemma, then we denote
in the previous lemma, then we denote  .
.
Lemma 2.5.
Let  be a real Banach space and
be a real Banach space and  the normalized duality mapping. Then for any
the normalized duality mapping. Then for any  in
in  and
and  , such that
, such that

Lemma 2.6 (see [7]).
Let  and
and  be three nonnegative real sequences, satisfying
be three nonnegative real sequences, satisfying

with  and
and  . Then,
. Then,  exists. In addition, if
exists. In addition, if  has a subsequence converging to zero, then
has a subsequence converging to zero, then  .
.
Proposition 2.7.
If  is a strict pseudocontraction, then
is a strict pseudocontraction, then  satisfies the Lipschitz condition
satisfies the Lipschitz condition

Proof.
By the definition of the strict pseudocontraction, we have

A simple computation shows the conclusion.
3. Main Results
Lemma 3.1.
Let  be a uniformly convex Banach space with the convex modulus of power type
be a uniformly convex Banach space with the convex modulus of power type  ,
,  a nonempty closed convex subset of
a nonempty closed convex subset of  satisfying
satisfying  , and
, and  hemicontractive mappings with
hemicontractive mappings with  . Let
. Let  ,
,  ,
,  ,
,  and
and  be the sequences in (II) and
be the sequences in (II) and

where  is the constant in Remark 2.4. Then,
is the constant in Remark 2.4. Then,
(1) exists for all
exists for all  ,
,
(2) exists,
exists,
-
(3)
if
 is continuous, then
is continuous, then 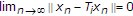 , for all
, for all 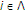 .
.
Proof. (1) Let  . By the boundedness assumption on
. By the boundedness assumption on  , there exists a constant
, there exists a constant  , for any
, for any  , such that
, such that  . From the definition of hemicontractive mappings, we have
. From the definition of hemicontractive mappings, we have

Using Lemmas 2.3, 2.5, and (3.2), we obtain

Hence,

It follows from (II) and Lemma 2.5 that

By the condition  , we may assume that
, we may assume that

Therefore,

Substituting (3.7) into (3.4), we get

Assumptions (i) and (ii) imply that there exists a positive integer  such that for every
such that for every  ,
,

Hence, for all  ,
,

where

From (3.9) and conditions (i) and (ii), it follows that

By Lemma 2.6, we see that  exists and the sequence
exists and the sequence  is bounded.
is bounded.
(2) It is easy to verify that  exists.
exists.
(3) By the boundedness of  , there exists a constant
, there exists a constant  such that
such that  , for all
, for all  . From (3.10), we get, for
. From (3.10), we get, for  ,
,

which implies

Thus,

It implies that

Therefore, by (3.7), we have

Using (II), we obtain

By a combination with the continuity of  (
( , we get
, we get

It is clear that for each  , there exists
, there exists  such that
such that  . Consequently,
. Consequently,

This completes the proof.
Theorem 3.2.
Let the assumptions of Lemma 3.1 hold, and let  be continuous. Then,
be continuous. Then,  converges strongly to a common fixed point of
converges strongly to a common fixed point of  if and only if
if and only if  .
.
Proof.
The necessity is obvious.
Now, we prove the sufficiency. Since  , it follows from Lemma 3.1 that
, it follows from Lemma 3.1 that  .
.
For any  , we have
, we have

Hence, we get

So,  is a Cauchy sequence in
is a Cauchy sequence in  . By the closedness of
. By the closedness of  , we get that the sequence
, we get that the sequence  converges strongly to
converges strongly to  . Let a sequence
. Let a sequence  , for some
, for some  , be such that
, be such that  converges strongly to
converges strongly to  . By the continuity of
. By the continuity of  , we obtain
, we obtain

Therefore,  . This implies that
. This implies that  is closed. Therefore,
is closed. Therefore,  is closed. By
is closed. By  , we get
, we get  . This completes the proof.
. This completes the proof.
Theorem 3.3.
Let the assumptions of Lemma 3.1 hold. Let  be continuous and
be continuous and  satisfy condition
satisfy condition . Then,
. Then,  converges strongly to a common fixed point of
converges strongly to a common fixed point of  .
.
Proof.
Since  satisfies condition
satisfies condition , and
, and  for each
for each  , it follows from the existence of
, it follows from the existence of  that
that  . Applying the similar arguments as in the proof of Theorem 3.2, we conclude that
. Applying the similar arguments as in the proof of Theorem 3.2, we conclude that  converges strongly to a common fixed point of
converges strongly to a common fixed point of  . This completes the proof.
. This completes the proof.
As a direct consequence of Theorem 3.3, we get the following result.
Corollary 3.4 (see [12, Theorem 3]).
Let H be a real Hilbert space,  a nonempty closed convex subset of
a nonempty closed convex subset of  satisfying
satisfying  , and
, and  continuous hemicontractive mapping which satisfies condition (A). Let
continuous hemicontractive mapping which satisfies condition (A). Let  be a real sequence in
be a real sequence in  with
with  . For any
. For any  , the sequence
, the sequence  is defined by
is defined by

Then,  converges strongly to a fixed point of
converges strongly to a fixed point of  .
.
Proof.
Employing the similar proof method of Lemma 3.1, we obtain by (3.10)

This implies

By  , we have
, we have  . Equation (3.7) implies that
. Equation (3.7) implies that 
 . Since
. Since  satisfies condition (A) and the limit
satisfies condition (A) and the limit  exists, we get
exists, we get  . The rest of the proof follows now directly from Theorem 3.2. This completes the proof.
. The rest of the proof follows now directly from Theorem 3.2. This completes the proof.
Remark 3.5.
Theorems 3.2 and 3.3 extend [12, Theorem 3] essentially since the following hold.
-
(i)
Hilbert spaces are extended to uniformly convex Banach spaces.
-
(ii)
The requirement of compactness on domain
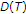 on [12, Theorem 3] is dropped.
on [12, Theorem 3] is dropped. -
(iii)
A single mapping is replaced by a family of mappings.
-
(iv)
The Mann-type implicit iteration is replaced by the generalized Mann iteration. So the restrictions of
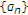 with
with 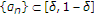 for some
for some 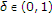 are relaxed to
are relaxed to  . The error term is also considered in the iteration (II).
. The error term is also considered in the iteration (II).
Moreover, if  , then
, then  is well defined by (II). Hence, Theorems 3.2 and 3.3 are also answers to the question proposed by Qing [13].
is well defined by (II). Hence, Theorems 3.2 and 3.3 are also answers to the question proposed by Qing [13].
Theorem 3.6.
Let  and
and  be as the assumptions of Lemma 3.1. Let
be as the assumptions of Lemma 3.1. Let  be strictly pseudocontractive mappings with
be strictly pseudocontractive mappings with  being nonempty. Let
being nonempty. Let  ,
,  ,
,  ,
,  , and
, and  be the sequences in (II) and
be the sequences in (II) and

where  is the constant in Remark 2.4. Then,
is the constant in Remark 2.4. Then,
(1) converges strongly to a common fixed point of
converges strongly to a common fixed point of  if and only if
if and only if  .
.
-
(2)
If
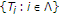 satisfies condition (
satisfies condition ( ) , then
) , then 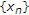 converges strongly to a common fixed point of
converges strongly to a common fixed point of  .
.
Remark 3.7.
Theorem 3.6 extends the corresponding result [6, Theorem 3.1].
References
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20(2):197-228. 10.1016/0022-247X(67)90085-6
Ceng L-C, Petruşel A, Yao J-C: Implicit iteration scheme with perturbed mapping for common fixed points of a finite family of Lipschitz pseudocontractive mappings. Journal of Mathematical Inequalities 2007, 1(2):243-258.
Chidume CE, Mutangadura SA: An example on the Mann iteration method for Lipschitz pseudocontractions. Proceedings of the American Mathematical Society 2001, 129(8):2359-2363. 10.1090/S0002-9939-01-06009-9
Chidume CE, Ali B: Weak and strong convergence theorems for finite families of asymptotically nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 2007, 330(1):377-387. 10.1016/j.jmaa.2006.07.060
Lin Y-C, Wong N-C, Yao J-C: Strong convergence theorems of Ishikawa iteration process with errors for fixed points of Lipschitz continuous mappings in Banach spaces. Taiwanese Journal of Mathematics 2006, 10(2):543-552.
Marino G, Xu H-K: Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007, 329(1):336-346. 10.1016/j.jmaa.2006.06.055
Osilike MO, Aniagbosor SC: Weak and strong convergence theorems for fixed points of asymptotically nonexpansive mappings. Mathematical and Computer Modelling 2000, 32(10):1181-1191. 10.1016/S0895-7177(00)00199-0
Prus B, Smarzewski R: Strongly unique best approximations and centers in uniformly convex spaces. Journal of Mathematical Analysis and Applications 1987, 121(1):10-21. 10.1016/0022-247X(87)90234-4
Reich S: Weak convergence theorems for nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1979, 67(2):274-276. 10.1016/0022-247X(79)90024-6
Takahashi W: Nonlinear Functional Analysis. Fixed Point Theory and Its Applications. Yokohama Publishers, Yokohama, Japan; 2000:iv+276.
Zeng L-C, Yao J-C: Implicit iteration scheme with perturbed mapping for common fixed points of a finite family of nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2006, 64(11):2507-2515. 10.1016/j.na.2005.08.028
Rafiq A: On Mann iteration in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2007, 66(10):2230-2236. 10.1016/j.na.2006.03.012
Qing Y: A note on "on Mann iteration in Hilbert spaces, Nonlinear Analysis 66 (2007) 2230–2236". Nonlinear Analysis: Theory, Methods & Applications 2008, 68(2):460. 10.1016/j.na.2007.08.056
Acknowledgments
The authors would like to thank the referees very much for helpful comments and suggestions. The work was supported partly by the National Natural Science Foundation of China, the Specialized Research Fund for the Doctoral Program of Higher Education of China, the NCET-04-0572 and Research Fund for the Key Program of the Chinese Academy of Sciences.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hu, LG., Xiao, TJ. & Liang, J. Generalized Mann Iterations for Approximating Fixed Points of a Family of Hemicontractions. Fixed Point Theory Appl 2008, 824607 (2008). https://doi.org/10.1155/2008/824607
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2008/824607
 with
with  is said to satisfy condition (A) on
is said to satisfy condition (A) on 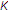 if there is a function
if there is a function 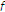 such that for all
such that for all  ,
, 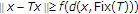 .
.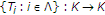 with
with 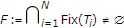 are said to satisfy condition (
are said to satisfy condition ( ) if there exists a function
) if there exists a function 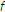 , such that
, such that 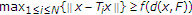 holds for all
holds for all  .
. is continuous, then
is continuous, then 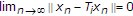 , for all
, for all 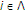 .
.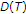 on [
on [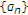 with
with 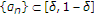 for some
for some 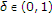 are relaxed to
are relaxed to  . The error term is also considered in the iteration (II).
. The error term is also considered in the iteration (II).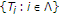 satisfies condition (
satisfies condition ( ) , then
) , then 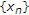 converges strongly to a common fixed point of
converges strongly to a common fixed point of  .
.