- Research
- Open access
- Published:
On some fixed point theorems under \((\alpha,\psi,\phi)\)-contractivity conditions in metric spaces endowed with transitive binary relations
Fixed Point Theory and Applications volume 2015, Article number: 124 (2015)
Abstract
After the appearance of Nieto and Rodríguez-López’s theorem, the branch of fixed point theory devoted to the setting of partially ordered metric spaces have attracted much attention in the last years, especially when coupled, tripled, quadrupled and, in general, multidimensional fixed points are studied. Almost all papers in this direction have been forced to present two results assuming two different hypotheses: the involved mapping should be continuous or the metric framework should be regular. Both conditions seem to be different in nature because one of them refers to the mapping and the other one is assumed on the ambient space. In this paper, we unify such different conditions in a unique one. By introducing the notion of continuity of a mapping from a metric space into itself depending on a function α, which is the case that covers the partially ordered setting, we extend some very recent theorems involving control functions that only must be lower/upper semi-continuous from the right. Finally, we use metric spaces endowed with transitive binary relations rather than partial orders.
1 Introduction
In recent times, some extensions of the Banach contractive mapping principle have been introduced using a contractivity condition that involves two different functions. For instance, in 2008, Dutta and Choudhury presented the following generalization.
Theorem 1.1
(Dutta and Choudhury [1])
Let \((X,d)\) be a complete metric space and let \(F:X\rightarrow X\) be a mapping such that
where \(\psi,\varphi:[0,\infty)\rightarrow{}[0,\infty)\) are continuous, nondecreasing and \(\psi^{-1}(\{0\})=\varphi^{-1}(\{0\})=\{0\}\). Then F has a unique fixed point.
Functions like ψ verifying the previous properties are known in the literature as altering distance functions (see [2]).
Remark 1.1
Notice that Theorem 1.1 remains true if φ only satisfies the following assumptions: φ is lower semi-continuous and \(\varphi^{-1}(\{0\})=\{0\}\) (see, for instance, Abbas and Đorić [3] and Đorić [4]).
The above remark yields the following statement.
Theorem 1.2
Let \((X,d)\) be a complete metric space and let \(F:X\rightarrow X \) be a mapping such that for each pair of points \(x,y\in X\),
where \(\psi:[0,\infty)\rightarrow{}[0,\infty)\) is continuous, nondecreasing, \(\psi^{-1}(\{0\})=\{0\}\), and \(\varphi:[0,\infty )\rightarrow{}[0,\infty)\) is lower semi-continuous and \(\varphi ^{-1}(\{0\})=\{0\}\). Then F has a unique fixed point.
We have also an ordered version of Theorem 1.2 (see [3–5]).
Theorem 1.3
Let \((X,\preccurlyeq)\) be a partially ordered set and suppose that there is a metric d on X such that \((X,d)\) is a complete metric space. Let \(F:X\rightarrow X\) be a continuous nondecreasing mapping such that
for all \(x,y\in X\) with \(x\preccurlyeq y\), where \(\psi:[0,\infty )\rightarrow{}[0,\infty)\) is continuous, nondecreasing, \(\psi ^{-1}(\{0\})=\{0\}\), and \(\varphi:[0,\infty)\rightarrow{}[0,\infty )\) is lower semi-continuous and \(\varphi^{-1}(\{0\})=\{0\}\). If there exists \(x_{0}\in X\) such that \(x_{0}\preccurlyeq Fx_{0}\), then F has a fixed point.
The previous results were extended to the case of a contractivity condition involving three different functions. For instance, Eslamian and Abkar [6] established the following result.
Theorem 1.4
(Eslamian and Abkar [6])
Let \((X,d)\) be a complete metric space and \(f:X\rightarrow X\) be such that
for all \(x,y\in X\), where \(\psi,\alpha,\beta:[0,\infty)\rightarrow {}[0,\infty)\) are such that ψ is continuous and nondecreasing, α is continuous, β is lower semi-continuous,
Then f has a unique fixed point.
Some of the previous results became equivalent.
Theorem 1.5
(Aydi et al. [7])
Theorem 1.4 and Theorem 1.2 are equivalent.
Choudhury and Kundu [8] also extended Theorem 1.4 to the ordered case.
Theorem 1.6
(Choudhury and Kundu [8])
Let \((X,\preccurlyeq)\) be a partially ordered set and suppose that there is a metric d on X such that \((X,d)\) is a complete metric space. Let \(f:X\rightarrow X\) be a continuous nondecreasing mapping such that
for all \(x,y\in X\) with \(x\preccurlyeq y\), where \(\psi,\alpha,\beta :[0,\infty)\rightarrow{}[0,\infty)\) are such that ψ is continuous and nondecreasing, α is continuous, β is lower semi-continuous,
If there exists \(x_{0}\in X\) such that \(x_{0}\preccurlyeq fx_{0}\), then f has a fixed point.
Following similar arguments as in the proof of Theorem 1.5, the following result was obtained.
Theorem 1.7
(Aydi et al. [7])
Theorem 1.3 and Theorem 1.6 are equivalent.
In a very recent paper, Shaddad et al. proved the following result, which is a generalization of the previous ones.
Theorem 1.8
(Shaddad et al. [9], Theorem 2.5)
Let \((X,d,\preccurlyeq)\) be a complete partially ordered metric space. Let \(f:X\rightarrow X\) be a mapping which obeys the following conditions:
-
1.
There exist an altering distance function ψ, an upper semi-continuous function \(\theta: [ 0,\infty ) \rightarrow [ 0,\infty ) \), and a lower semi-continuous function \(\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that
$$\psi \bigl( d(fx,fy) \bigr) \leq\theta \bigl( d(x,y) \bigr) -\varphi \bigl( d(x,y) \bigr)\quad \textit{for all }x\succcurlyeq y, $$where \(\theta(0)=\varphi(0)=0\) and \(\psi(t)-\theta(t)+\varphi(t)>0\) for all \(t>0\).
-
2.
There exists \(x_{0}\in X\) such that \(x_{0}\asymp f(x_{0})\);
-
3.
f is nondecreasing;
-
4.
At least, one of the following conditions holds:
-
(a)
f is continuous or
-
(b)
if \(\{x_{n}\}\rightarrow x\) when \(n\rightarrow\infty\) in X, then \(x_{n}\asymp x\) for all n.
-
(a)
Then f has a fixed point. Moreover, if for each \(x,y\in X\) there exists \(z\in X\) which is comparable to x and y, then the fixed point is unique.
The condition ‘\(\psi(t)-\theta(t)+\varphi(t)>0\) for all \(t>0\)’ is not new because, as we have just commented, under some weak continuity conditions, it was firstly considered in Choudhury and Kundu [8], and it can also be found in Razani and Parvaneh [10]. As a consequence of the previous theorem, the authors obtained the following result.
Corollary 1.1
(Shaddad et al. [9], Corollary 2.6)
Let \((X,d,\preccurlyeq)\) be a complete partially ordered metric space. Let \(f:X\rightarrow X\) be a mapping which obeys the following conditions:
-
1.
There exist an altering distance function ψ and a lower semi-continuous function \(\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that
$$ \psi \bigl( d(fx,fy) \bigr) \leq\psi \bigl( d(x,y) \bigr) -\varphi \bigl( d(x,y) \bigr)\quad \textit{for all }x\succcurlyeq y, $$(1)where \(\varphi(0)=0\);
-
2.
There exists \(x_{0}\in X\) such that \(x_{0}\asymp f(x_{0})\);
-
3.
f is nondecreasing;
-
4.
At least, one of the following conditions holds:
-
(a)
f is continuous or
-
(b)
if \(\{x_{n}\}\rightarrow x\) when \(n\rightarrow\infty\) in X, then \(x_{n}\asymp x\) for all n.
-
(a)
Then f has a fixed point. Moreover, if for each \(x,y\in X\) there exists \(z\in X\) which is comparable to x and y, then the fixed point is unique.
Two remarks must be done concerning the previous statements. On the one hand, condition 4(b) in Theorem 1.8 is unclear. We suppose that it means that \((X,d,\preccurlyeq)\) is a regular partially ordered metric space, that is, it verifies the following two properties:
-
if \(\{x_{m}\}\subseteq X\) is such that \(\{x_{m}\}\rightarrow x\in X\) and \(x_{m}\preccurlyeq x_{m+1}\) for all \(m\in\mathbb{N}\), then we have that \(x_{m}\preccurlyeq x\) for all \(m\in\mathbb{N}\);
-
if \(\{x_{m}\}\subseteq X\) is such that \(\{x_{m}\}\rightarrow x\in X\) and \(x_{m}\succcurlyeq x_{m+1}\) for all \(m\in\mathbb{N}\), then we have that \(x_{m}\succcurlyeq x\) for all \(m\in\mathbb{N}\).
On the other hand, in hypothesis 1 of Corollary 1.1, the condition ‘\(\varphi(t)>0\) for all \(t>0\)’ is necessary. For instance, consider the following example.
Example 1.1
Let \(X=\mathbb{N}\setminus\{0\}\) be endowed with the usual partial order ≤ and the Euclidean metric \(d(x,y)=\vert x-y\vert \) for all \(x,y\in X\). Then \(( \mathbb{N}\setminus\{0\},d,\leq ) \) is a complete partially ordered metric space. Let define \(f:X\rightarrow X\) by \(f(n)=n+1\) for all \(n\in X\). Then f does not have any fixed point on X. However, if we define
then ψ is an altering distance function satisfying assumption (1), where \(\varphi(t)=0\) for all \(t\in [ 0,\infty ) \) (because \(\psi(n)=1\) for all \(n\in X\)). Hence, Corollary 1.1 is false if we omit the condition ‘\(\varphi(t)>0\) for all \(t>0\)’, that is, \(\varphi(t)=0\) if, and only if, \(t=0\).
This paper has three main aims. On the one hand, we generalize Theorem 1.1 introducing a contractivity condition involving control function that does not have to be continuous nor monotone. In fact, this new kind of control functions only have to verify sequential properties. We will show that two functions are powerful enough to handle contractivity conditions as in hypothesis 1 of Theorem 1.8, in which three functions appear. The new class of control functions includes pairs that are not necessary altering distance functions, and the semi-continuity is imposed only from the right side and on the interval \(( 0,\infty ) \). On the other hand, the second objective is to describe a unified condition to handle two independent hypotheses (the continuity of a mapping and the regularity of the partially ordered metric space), which were initially introduced from Ran and Reurings’ theorem and Nieto and Rodríguez-López’s theorem. Finally, we show that many results obtained in the setting of a partially ordered metric space do not need a partial order, but only a transitive binary relation on a subset of the metric space.
2 Preliminaries
In the sequel, \(\mathbb{N}=\{0,1,2,3,\ldots\}\) denotes the set of all nonnegative integers and \(\mathbb{R}\) denotes the set of all real numbers. Henceforth, X and Y will denote nonempty sets. Elements of X are usually called points.
Let \(T:X\rightarrow Y\) be a mapping. The domain of T is X and it is denoted by DomT. Its range, that is, the set of values of T in Y, is denoted by \(T(X)\). A mapping T is completely characterized by its domain, its range, and the manner in which each origin \(x\in\operatorname{Dom}T\) is applied to its image \(T(x)\in T(X)\). For simplicity, we denote, as usual, \(T(x)\) by Tx. For any set X, we denote the identity mapping on X by \(I_{X}:X\rightarrow X\), which is defined by \(I_{X}x=x\) for all \(x\in X\).
Given two self-mappings \(T,g:X\rightarrow X\), we will say that a point \(x\in X\) is a coincidence point of T and g if \(Tx=gx\). We will denote by \(\operatorname{Coin}(T,g)\) the set of all coincidence points of T and g. If x is a coincidence point of T and g, then the point \(\omega=Tx=gx\) is called a point of coincidence of T and g. A common fixed point of T and g is a point \(x\in X\) such that \(Tx=gx=x\). Given a self-mapping \(T:X\rightarrow X\), we will say that a point \(x\in X\) is a fixed point of T if \(Tx=x\). We will denote by \(\operatorname{Fix}(T)\) the set of all fixed points of T.
Given two mappings \(T:X\rightarrow Y\) and \(S:Y\rightarrow Z\), the composite of T and S is the mapping \(S\circ T:X\rightarrow Z\) given by
We say that two self-mappings \(T,S:X\rightarrow X\) are commuting if \(TSx=STx\) for all \(x\in X\) (that is, \(T\circ S=S\circ T\)).
The iterates of a self-mapping \(T:X\rightarrow X\) are the mappings \(\{T^{n}:X\rightarrow X\}_{n\in\mathbb{N}}\) defined by
The notion of metric space and the concepts of convergent sequence and Cauchy sequence in a metric space can be found, for instance, in [11]. We will write \(\{x_{n}\}\rightarrow x\) when a sequence \(\{x_{n}\}_{n\in\mathbb{N}}\) of points of X converges to \(x\in X\) in the metric space \(( X,d ) \). A metric space \(( X,d ) \) is complete if every Cauchy sequence in X converges to some point of X. The limit of a convergent sequence in a metric space is unique.
In a metric space \(( X,d ) \), a mapping \(T:X\rightarrow X\) is continuous at a point \(z\in X\) if \(\{Tx_{n}\}\rightarrow Tz\) for all sequence \(\{x_{n}\}\) in X such that \(\{x_{n}\}\rightarrow z\). And T is continuous if it is continuous at every point of X.
A binary relation on
X is a nonempty subset \(\mathcal{R}\) of \(X\times X\). For simplicity, we denote  if \((x,y)\in \mathcal{R}\), and we will say that
if \((x,y)\in \mathcal{R}\), and we will say that  is the binary relation on X. This notation lets us write \(x\prec y\) when
is the binary relation on X. This notation lets us write \(x\prec y\) when  and \(x\neq y\). We write
and \(x\neq y\). We write  when
when  . We will say that x and y are
. We will say that x and y are  -comparable, and we will write \(x\asymp y\) if
-comparable, and we will write \(x\asymp y\) if  or
or  . A binary relation
. A binary relation  on X is reflexive if
on X is reflexive if  for all \(x\in X\); it is transitive if
for all \(x\in X\); it is transitive if  for all \(x,y,z\in X\) such that
for all \(x,y,z\in X\) such that  and
and  ; and it is antisymmetric if
; and it is antisymmetric if  and
and  imply \(x=y\).
imply \(x=y\).
A reflexive and transitive relation ≼ on X is a preorder (or a quasiorder) on X. In such a case, \((X,\preccurlyeq)\) is a preordered space. If a preorder ≼ is also antisymmetric, then ≼ is called a partial order, and \((X,\preccurlyeq)\) is a partially ordered space (or a partially ordered set). We will use the symbol  for a general binary relation on X, and the symbol ≼ for a reflexive binary relation on X (for instance, a preorder or a partial order).
for a general binary relation on X, and the symbol ≼ for a reflexive binary relation on X (for instance, a preorder or a partial order).
The usual order of the set of all real numbers \(\mathbb{R}\) is denoted by ≤. In fact, this partial order can be induced on any nonempty subset \(A\subseteq\mathbb{R}\). Let ≼ be the binary relation on \(\mathbb{R}\) given by
Then ≼ is a partial order on \(\mathbb{R}\), but it is different from ≤. Any equivalence relation is a preorder.
An ordered metric space is a triple \(( X,d,\preccurlyeq ) \) where \(( X,d ) \) is a metric space and ≼ is a partial order on X. And if ≼ is a preorder on X, then \(( X,d,\preccurlyeq ) \) is a preordered metric space.
Definition 2.1
Let \(( X,d ) \) be a metric space, let \(A\subseteq X\) be a nonempty subset, and let  be a binary relation on X. Then
be a binary relation on X. Then  is said to be:
is said to be:
-
nondecreasing-regular if for all sequence \(\{x_{m}\} \subseteq A \) such that \(\{x_{m}\}\rightarrow a\in A\) and
 for all \(m\in\mathbb{N}\), we have that
for all \(m\in\mathbb{N}\), we have that 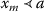 for all \(m\in\mathbb{N}\);
for all \(m\in\mathbb{N}\); -
nonincreasing-regular if for all sequence \(\{x_{m}\} \subseteq A \) such that \(\{x_{m}\}\rightarrow a\in A\) and
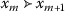 for all \(m\in\mathbb{N}\), we have that
for all \(m\in\mathbb{N}\), we have that 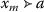 for all \(m\in\mathbb{N}\);
for all \(m\in\mathbb{N}\); -
regular if it is both nondecreasing-regular and nonincreasing-regular.
Some authors called ordered complete to a regular ordered metric space (see, for instance, [12]). Furthermore, Roldán et al. called sequential monotone property to nondecreasing-regularity (see [13]).
Definition 2.2
Let  be a binary relation on X and let \(T,g:X\rightarrow X\) be two mappings. We say that T is
be a binary relation on X and let \(T,g:X\rightarrow X\) be two mappings. We say that T is  -nondecreasing if
-nondecreasing if  for all \(x,y\in X\) such that
for all \(x,y\in X\) such that  . And T is
. And T is  -nondecreasing if
-nondecreasing if  for all \(x,y\in X\) such that
for all \(x,y\in X\) such that  .
.
Let us consider the following families of control functions.
Functions in \(\mathcal{F}_{\mathrm{alt}}\) are called altering distance functions (see [2, 14–16]).
Remark 2.1
If \(\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) is nondecreasing (for instance, if \(\phi\in{\mathcal {F}_{\mathrm{alt}}}\)) and \(t,s\in [ 0,\infty ) \) verify \(\phi(t)<\phi(s) \), then \(t< s\).
To prove it, assume that \(t\geq s\). As ϕ is nondecreasing, then \(\phi(s)\leq\phi(t)<\phi(s)\), which is impossible.
Definition 2.3
Let \(s\in [ 0,\infty ) \) be a point and let \(A\subseteq [ 0,\infty ) \) be a nonempty subset. We will say that a function \(\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) is
-
lower semi-continuous from the right at \(s\in [ 0,\infty ) \) if
$$\phi(s)\leq\liminf_{t\rightarrow s^{+}}\phi(t); $$ -
lower semi-continuous from the right on A if it is lower semi-continuous from the right at every \(s\in A\);
-
lower semi-continuous from the right if it is lower semi-continuous from the right on \([ 0,\infty ) \).
Similarly, we will say that ϕ is upper semi-continuous from the right at \(s\in [ 0,\infty ) \) if
and ϕ is upper semi-continuous from the right if it is upper semi-continuous from the right at every \(s\in [ 0,\infty )\).
Example 2.1
The function \(\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) defined, for all \(t\in [ 0,\infty ) \), by
is strictly increasing and lower semi-continuous from the right, but it is not lower semi-continuous at \(t=1\).
Lemma 2.1
Let \((X,d)\) be a metric space and let \(\{x_{n}\} \subseteq X\) be a sequence which is not Cauchy in \(( X,d ) \). Then there exist \(\varepsilon_{0}>0\) and two subsequences \(\{x_{n(k)}\}\) and \(\{x_{m(k)}\}\) of \(\{x_{n}\}\) such that
Furthermore, if \(\{d(x_{n},x_{n+1})\}\rightarrow0\), then
3 Main results
In this section, we present some results that extend and unify all theorems given in Introduction. To do that, some notions are introduced. In the sequel, X will denote a nonempty set, d will be a metric on X, \(T,g:X\rightarrow X\) will be arbitrary self-mappings and \(\alpha:X\times X\rightarrow{}[0,\infty)\) will denote a function.
Definition 3.1
Given a metric space \((X,d)\), a point \(z_{0}\in X\), a function \(\alpha:X\times X\rightarrow{}[0,\infty)\) and two mappings \(T,g:X\rightarrow X\), we say that T is \((d,g,\alpha )\)-right-continuous at \(z_{0}\) if we have that \(\{Tx_{n}\}\) converges to \(Tz_{0}\) for all sequence \(\{x_{n}\}\subseteq X\) such that \(\{ gx_{n}\}\) is convergent to \(gz_{0}\) and verifying that \(\alpha ( gx_{n},gx_{n+1} ) \geq1\) for all \(n\in\mathbb{N}\). And T is \((d,g,\alpha )\)-right-continuous if it is \((d,g,\alpha)\)-right-continuous at every point of X. If g is the identity mapping on X, we say that T is \((d,\alpha)\)-right-continuous.
Similarly, a mapping \(T:X\rightarrow X\) is \((d,g,\alpha )\)-left-continuous at \(z_{0}\) if we have that \(\{Tx_{n}\}\) converges to \(Tz_{0}\) for all sequence \(\{x_{n}\}\) such that \(\{gx_{n}\}\) is convergent to \(gz_{0}\) and verifying that \(\alpha ( gx_{n+1},gx_{n} ) \geq1\) for all \(n\in\mathbb{N}\). And T is \((d,g,\alpha)\)-left-continuous if it is \((d,g,\alpha)\)-left-continuous at every point of X. If g is the identity mapping on X, we say that T is \((d,\alpha)\)-left-continuous.
A mapping \(T:X\rightarrow X\) is \((d,g,\alpha)\)-continuous if it is both \((d,g,\alpha)\)-right-continuous and \((d,g,\alpha )\)-left-continuous.
If \(\alpha(x,y)=1\) for all \(x,y\in X\), we say that T is \((d,g)\)-continuous (notice that both sides lead to the same condition) if \(\{gx_{n}\}\rightarrow gz_{0}\) implies that \(\{Tx_{n}\}\rightarrow Tz_{0}\), whatever the point \(z_{0}\in X\) and the sequence \(\{x_{n}\}\subseteq X\).
It is obvious that every continuous mapping from X into itself is also \(( d,I_{X},\alpha ) \)-right-continuous and \(( d,I_{X},\alpha ) \)-left-continuous whatever α, but the converse is false.
Definition 3.2
Given a function \(\alpha:X\times X\rightarrow{}[0,\infty)\), we say that two points \(x,y\in X\) are \((g,\alpha)\)-comparable if \(\alpha(gx,gy)\geq1\) or \(\alpha(gy,gx)\geq1\).
Definition 3.3
We say that a function \(\alpha:X\times X\rightarrow{}[0,\infty)\) is transitive if, for all \(x,y,z\in X\), we have
Similarly, we say that α is g-transitive if, for all \(x,y,z\in X\), we have
Obviously, every transitive mapping α is also g-transitive, whatever the mapping g.
Definition 3.4
Let \(T:X\rightarrow X\) and \(\alpha:X\times X\rightarrow{}[0,\infty )\) be two mappings. We say that T is \((g,\alpha)\)-admissible if, for all \(x,y\in X\), we have
Example 3.1
If \(\alpha(x,y)\geq1\) for all \(x,y\in X\), then α is transitive and g-transitive, and every self-mapping \(T:X\rightarrow X\) is \((g,\alpha )\)-admissible.
Remark 3.1
Given a binary relation  on X, let
on X, let  be the function defined by
be the function defined by

-
The binary relation
 is transitive if, and only if,
is transitive if, and only if, 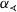 is transitive.
is transitive. -
A self-mapping \(T:X\rightarrow X\) is
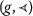 -nondecreasing if, and only if, T is
-nondecreasing if, and only if, T is  -admissible.
-admissible.
In the next definition, we present the kind of control functions we will involve in the contractivity condition.
Definition 3.5
Let \(\mathcal{F}_{\mathcal{A}}\) be the family of all pairs \(( \psi,\phi ) \) where \(\psi,\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) are two functions verifying the following two conditions:
- (\(\mathcal{F}_{\mathcal{A}}^{1} \)):
-
If \(\{a_{n}\}\subset ( 0,\infty ) \) is a sequence such that \(\psi ( a_{n+1} ) \leq\phi(a_{n})\) for all \(n\in\mathbb{N}\), then \(\{a_{n}\}\rightarrow0\);
- (\(\mathcal{F}_{\mathcal{A}}^{2}\)):
-
If \(\{a_{n}\},\{b_{n}\}\subset [ 0,\infty ) \) are two sequences converging to the same limit L and such that \(L< a_{n}\) and \(\psi ( b_{n} ) \leq\phi(a_{n})\) for all \(n\in\mathbb{N}\), then \(L=0\).
Notice that the previous conditions do not impose any constraint about the continuity nor the monotony of the functions ψ and ϕ, as in the following example.
Example 3.2
Let \(\psi,\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) be the functions given, for all \(t\in [ 0,\infty ) \), by
Then ψ and ϕ are not continuous nor monotone in \([ 0,\infty ) \). However, \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\). To prove it, notice that
Let \(\{a_{n}\}\subset ( 0,\infty ) \) be a sequence such that \(\psi ( a_{n+1} ) \leq\phi(a_{n})\) for all \(n\in\mathbb{N}\). Therefore,
Hence, \(\{\psi(a_{n})\}\rightarrow0\). It follows that there exists \(n_{0}\in\mathbb{N}\) such that \(\psi(a_{n})<1/4\) for all \(n\geq n_{0}\). By (3), \(a_{n}\leq1/2\) for all \(n\geq n_{0}\). In such a case, \(a_{n}=2\psi(a_{n})\) for all \(n\geq n_{0}\), so \(\{a_{n}\}\rightarrow0\). As a consequence, (\(\mathcal{F}_{\mathcal{A}}^{1}\)) holds.
Next, assume that \(\{a_{n}\},\{b_{n}\}\subset [ 0,\infty ) \) are two sequences converging to the same limit L and such that \(L< a_{n}\) and \(\psi ( b_{n} ) \leq\phi(a_{n})\) for all \(n\in\mathbb{N}\). We distinguish two cases.
-
Suppose that \(L=1\). As \(1=L< a_{n}\) for all \(n\in\mathbb{N}\), then \(\psi(a_{n})=a_{n}/4\) and \(\{\psi(a_{n})\}\rightarrow L/4=1/4\). On the other hand, as \(1/4\leq\psi(t)\) for all \(t\in(0.9,1.1)\) and \(\{b_{n}\} \rightarrow1\), then there exists \(n_{0}\in\mathbb{N}\) such that
$$\frac{1}{4}\leq\psi(b_{n})\leq\phi(a_{n})= \frac{\psi(a_{n})}{2}=\frac {a_{n}}{8} \quad \text{for all }n\geq n_{0}, $$which is a contradiction because \(\{a_{n}/8\}\rightarrow1/8\). Hence, the case \(L=1\) is impossible.
-
Suppose that \(L\neq1\). As ψ and ϕ are continuous at L, then the inequality
$$\psi ( b_{n} ) \leq\phi(a_{n})=\frac{\psi(a_{n})}{2} \quad \text{for all }n\in\mathbb{N} $$implies that \(\psi(L)\leq\psi(L)/2\). Hence, \(\psi(L)=0\) and \(L=0\).
Let us show that the class \(\mathcal{F}_{\mathcal{A}}\) includes several types of functions.
Lemma 3.1
If \(\psi,\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) are two functions such that ψ is continuous on \(( 0,\infty ) \), ϕ is upper semi-continuous from the right on \(( 0,\infty ) \), and \(\phi<\psi\) on \(( 0,\infty ) \), then \(( \psi,\phi ) \) verifies (\(\mathcal{F}_{\mathcal {A}}^{2}\)).
Furthermore, if, additionally, ψ is nondecreasing on \(( 0,\infty ) \), then \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\).
Proof
Let \(\{a_{n}\},\{b_{n}\}\subset [ 0,\infty ) \) be two sequences converging to the same limit \(L\in [ 0,\infty ) \) and such that \(L< a_{n}\) and \(\psi ( b_{n} ) \leq\phi(a_{n})\) for all \(n\in\mathbb{N}\). We are going to show that \(L=0\) reasoning by contradiction. Assume that \(L>0\). As \(a_{n}>L>0\) for all \(n\in\mathbb{N}\), then \(\phi (a_{n})<\psi(a_{n})\). Hence,
Since ψ is continuous at \(L\in ( 0,\infty ) \), then \(\{\psi(a_{n})\}\rightarrow\psi(L)\) and \(\{\psi(b_{n})\}\rightarrow\psi(L)\). Therefore, by (4), we also have that \(\{\phi(a_{n})\}\rightarrow\psi(L)\). Since \(\{a_{n}\}\rightarrow L^{+}\), the upper semi-continuity from the right of ϕ in \(( 0,\infty ) \) yields
As a consequence,
which is a contradiction. Thus, \(L=0\).
Next, assume that ψ is nondecreasing on \(( 0,\infty ) \) and let \(\{a_{n}\}\subset ( 0,\infty ) \) be a sequence such that \(\psi ( a_{n+1} ) \leq\phi(a_{n})\) for all \(n\in\mathbb{N}\). Since \(a_{n}>0\), then
By Remark 2.1, \(a_{n+1}< a_{n}\) for all \(n\in\mathbb{N}\). As \(\{a_{n}\}\) is a decreasing sequence of positive real numbers, then it is convergent. Let L be its limit. We are going to show that \(L=0\) reasoning by contradiction. Assume that \(L>0\). Hence, \(L< a_{n+1}< a_{n}\) for all \(n\in\mathbb{N}\), which means that \(\{a_{n}\}\rightarrow L^{+}\). Repeating, point by point, the previous arguments, we deduce that
which is a contradiction. As a consequence, \(L=0\) and \(\{a_{n}\} \rightarrow0\). □
Corollary 3.1
If \(\psi\in{\mathcal{F}_{\mathrm{alt}}}\) and \(\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) is an upper semi-continuous from the right function such that \(\phi(0)=0\) and \(\phi(t)<\psi(t)\) for all \(t>0\), then \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\).
Corollary 3.2
If ψ, θ and φ are three functions as in hypothesis 1 of Theorem 1.8, then \(( \psi,\phi=\theta-\varphi ) \in\mathcal{F}_{\mathcal{A}}\).
The main result of the present paper is the following one.
Theorem 3.1
Let \((X,d)\) be a metric space, let \(\alpha:X\times X\rightarrow{}[0,\infty)\) be a function, and let \(T,g:X\rightarrow X\) be two mappings such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\subseteq g(X)\) and \(( A,d ) \) is complete;
-
2.
α is g-transitive and T is \((g,\alpha)\)-admissible;
-
3.
There exists \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\) such that
$$ \alpha(gx,gy) \psi \bigl( d(Tx,Ty) \bigr) \leq\phi \bigl( d(gx,gy) \bigr)\quad \textit{for all }x,y\in X; $$(5) -
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that \(\alpha (gx_{0},Tx_{0})\geq1\) and T is \((d,g,\alpha)\)-right-continuous;
-
(b)
there exists \(x_{0}\in X\) such that \(\alpha (Tx_{0},gx_{0})\geq1\) and T is \((d,g,\alpha)\)-left-continuous.
-
(a)
Then T and g have, at least, a coincidence point.
Proof
Starting from the point \(x_{0}\in X\) given by hypothesis 4, condition 1 guarantees that there exists a Picard-Jungck sequence of \(( T,g ) \) based on \(x_{0}\), that is, a sequence \(\{x_{n}\}\subseteq X\) which verifies \(gx_{n+1}=Tx_{n}\) for all \(n\in\mathbb{N}\). If there exists some \(n_{0}\in\mathbb{N}\) such that \(gx_{n_{0}}=gx_{n_{0}+1}\), then \(gx_{n_{0}}=gx_{n_{0}+1}=Tx_{n_{0}}\), so \(x_{n_{0}}\) is a coincidence point of T and g, and the proof is finished. On the contrary, assume that \(gx_{n}\neq gx_{n+1}\) for all \(n\in\mathbb{N}\), that is,
We are going to show that \(\{gx_{n}\}\) converges to a point of coincidence of T and g assuming hypothesis 4(a), that is, supposing that \(\alpha(gx_{0},Tx_{0})\geq1\) and T is \((d,g,\alpha)\)-right-continuous (the other case is similar). As \(\alpha(gx_{0},gx_{1})=\alpha(gx_{0},Tx_{0})\geq1\) and T is \((g,\alpha )\)-admissible, then \(\alpha(gx_{1},gx_{2})=\alpha(Tx_{0},Tx_{1})\geq1\). By induction, we obtain that
Moreover, as α is g-transitive, then, if \(n< m\),
As a result,
Applying the contractivity condition (5) to \(x=x_{n}\) and \(y=x_{n+1}\), we obtain that
for all \(n\in\mathbb{N}\). Since \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\), then \(\{d(gx_{n},gx_{n+1})\}\rightarrow0\) by property (\(\mathcal{F}_{\mathcal{A}}^{1}\)).
Next, we show that \(\{gx_{n}\}\) is a Cauchy sequence in \((X,d)\) reasoning by contradiction. Assume that \(\{gx_{n}\}\) is not Cauchy. By Lemma 2.1, there exists \(\varepsilon_{0}>0\) and two subsequences \(\{gx_{n(k)}\}\) and \(\{gx_{m(k)}\}\) of \(\{gx_{n}\}\) such that
and also
As a consequence, there exists \(k_{0}\in\mathbb{N}\) such that
As \(n(k)< m(k)\), by (7) we have that \(\alpha(gx_{n(k)},gx_{m(k)})\geq1\) for all \(k\geq k_{0}\). Hence, the contractivity condition (5) yields
for all \(k\geq k_{0}\). Applying condition (\(\mathcal{F}_{\mathcal {A}}^{2}\)) to
we deduce that \(\varepsilon_{0}=L=0\), which is a contradiction. This contradiction guarantees that \(\{gx_{n}\}\) is a Cauchy sequence in \((X,d)\). Since \(\{gx_{n+1}\}_{n\in\mathbb{N}}=\{Tx_{n}\}_{n\in\mathbb {N}}\subseteq T(X)\subseteq A\) and \(( A,d ) \) is complete, there exists \(u_{0}\in A\) such that \(\{gx_{n}\}\rightarrow u_{0}\). Moreover, as \(u_{0}\in A\subseteq g(X)\), then there exists \(z_{0}\in X\) such that \(gz_{0}=u_{0}\). Taking into account that T is \((d,g,\alpha)\)-right-continuous and (6), it follows that
But as \(Tx_{n}=gx_{n+1}\) for all \(n\in\mathbb{N}\) and \(\{gx_{n}\} \rightarrow gz_{0}\), the uniqueness of the limit of a convergent sequence in a metric space allows us to conclude that \(Tz_{0}=gz_{0}\), that is, \(z_{0}\) is a coincidence point of T and g. □
Theorem 3.2
Under the hypothesis of Theorem 3.1, assume that \(\phi(0)=0\) and \(\psi^{-1}(\{0\})=\{0\}\). If x and y are two coincidence points of T and g for which there exists \(z\in X\) such that z is, at the same time, \((g,\alpha)\)-comparable to x and to y, then \(Tx=gx=gy=Ty\).
Proof
Let \(x,y\in\operatorname{Coin}(T,g)\) be two coincidence points of T and g for which there exists \(z_{0}\in X\) such that \(z_{0}\) is, at the same time, \((g,\alpha)\)-comparable to x and to y. Let \(\{z_{n}\}\) be the Picard-Jungck sequence of \(( T,g ) \) based on \(z_{0}\), that is, \(gz_{n+1}=Tz_{n}\) for all \(n\in\mathbb{N}\). We are going to show that \(\{gz_{n}\}\rightarrow gx\) and \(\{gz_{n}\}\rightarrow gy\) so, by the uniqueness of the limit, we will conclude that \(gx=gy\).
Firstly, we show that \(\{gz_{n}\}\rightarrow gx\). Assume, for instance, that \(\alpha(gz_{0},gx)\geq1\). As T is \((g,\alpha)\)-admissible, then \(\alpha(gz_{1},gx)=\alpha(Tz_{0},Tx)\geq1\). By induction, we deduce that \(\alpha(gz_{n},gx)\geq1\) for all \(n\in\mathbb{N}\). Using the contractivity condition (5),
for all \(n\in\mathbb{N}\). Next, we distinguish two cases.
-
If there exists some \(n_{0}\in\mathbb{N}\) such that \(d(gz_{n_{0}},gx)=0\), then \(\psi ( d(gz_{n_{0}+1},gx) ) \leq\phi ( 0 ) =0\), so \(gz_{n_{0}+1}=gx\). In this case, by induction, we deduce that \(gz_{n}=gx\) for all \(n\geq n_{0}\), which implies that \(\{gz_{n}\}\rightarrow gx\).
-
On the contrary case, assume that \(d(gz_{n},gx)>0\) for all \(n\in\mathbb{N}\). In such a case, property (\(\mathcal{F}_{\mathcal {A}}^{1} \)) applied to \(\{a_{n}=d(gz_{n},gx)\}_{n\in\mathbb{N}}\subset ( 0,\infty ) \) guarantees that \(\{d(gz_{n},gx)\} \rightarrow 0\), that is, \(\{gz_{n}\}\rightarrow gx\).
If we had supposed that \(\alpha(gx,gz_{0})\geq1\), we would have obtained the same conclusion. Then, in any case, \(\{gz_{n}\}\rightarrow gx\). Changing the roles of x and y, we also have that \(\{gz_{n}\}\rightarrow gy\). Therefore \(gx=gy\). □
Theorem 3.3
Under the hypothesis of Theorem 3.1, assume that T and g commute, \(\phi(0)=0\), \(\psi^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all coincidence points x and y of T and g, there exists \(z\in X\) such that z is, at the same time, \((g,\alpha )\)-comparable to x and to y.
Hence T and g have a unique common fixed point \(\omega\in X\). Furthermore, \(\omega=gx\) for all \(x\in\operatorname{Coin}(T,g)\).
Proof
Let \(x\in\operatorname{Coin}(T,g)\) be an arbitrary coincidence point of T and g and let \(\omega=gx\). As T and g commute, then \(T\omega=Tgx=gTx=g\omega\), so ω is another coincidence point of T and g. By hypothesis (U), there exists \(z\in X\) such that z is, at the same time, \((g,\alpha)\)-comparable to x and to ω. Hence, Theorem 3.2 guarantees that \(gx=g\omega\), which means that \(\omega=gx=g\omega\). As a result, \(\omega=g\omega=T\omega\), that is, ω is a common fixed point of T and g.
To prove the uniqueness, let \(u,v\in X\) be two common fixed points of T and g. As u and v are coincidence points of T and g, hypothesis (U) implies that there exists \(z\in X\) such that z is, at the same time, \((g,\alpha)\)-comparable to u and to v. Thus, Theorem 3.2 guarantees that \(gu=gv\), which means that \(u=gu=gv=v\). As a consequence, T and g have a unique common fixed point, which is ω. □
4 Consequences of the main results
The best advantage of the previous theorems is that they can be particularized in a wide variety of different results. This section is dedicated to deducing some direct consequences of them in the context of metric spaces. For instance, in the following statement we use Lemma 3.1.
Corollary 4.1
Let \((X,d)\) be a metric space, let \(\alpha :X\times X\rightarrow{}[0,\infty)\) be a function, and let \(T,g:X\rightarrow X\) be two mappings such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\subseteq g(X)\) and \(( A,d ) \) is complete;
-
2.
α is g-transitive and T is \((g,\alpha)\)-admissible;
-
3.
There exist two functions \(\psi,\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that ψ is continuous and nondecreasing on \(( 0,\infty ) \), ϕ is upper semi-continuous from the right on \(( 0,\infty ) \), \(\phi<\psi\) on \(( 0,\infty ) \), and the following inequality holds:
$$\alpha(gx,gy) \psi \bigl( d(Tx,Ty) \bigr) \leq\phi \bigl( d(gx,gy) \bigr)\quad \textit{for all }x,y\in X; $$ -
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that \(\alpha (gx_{0},Tx_{0})\geq1\) and T is \((d,g,\alpha)\)-right-continuous;
-
(b)
there exists \(x_{0}\in X\) such that \(\alpha (Tx_{0},gx_{0})\geq1\) and T is \((d,g,\alpha)\)-left-continuous.
-
(a)
Then T and g have, at least, a coincidence point.
Additionally, assume that T and g commute, \(\phi(0)=0\), \(\psi ^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all coincidence points x and y of T and g, there exists \(z\in X\) such that z is, at the same time, \((g,\alpha )\)-comparable to x and to y.
Then T and g have a unique common fixed point \(\omega\in X\). Furthermore, \(\omega=gx\) for all \(x\in\operatorname{Coin}(T,g)\).
Proof
It follows from Theorems 3.1 and 3.3 taking into account that, by Lemma 3.1, \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\). □
In the following result, we use a different contractivity condition involving three control functions by decomposing \(\phi=\theta-\varphi\).
Corollary 4.2
Let \((X,d)\) be a metric space, let \(\alpha :X\times X\rightarrow{}[0,\infty)\) be a function, and let \(T,g:X\rightarrow X\) be two mappings such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\subseteq g(X)\) and \(( A,d ) \) is complete;
-
2.
α is g-transitive and T is \((g,\alpha)\)-admissible;
-
3.
There exist three functions \(\psi,\theta,\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that ψ is continuous and nondecreasing on \(( 0,\infty ) \), θ is upper semi-continuous from the right on \(( 0,\infty ) \), φ is lower semi-continuous from the right on \(( 0,\infty ) \), \(\theta-\varphi<\psi\) on \(( 0,\infty ) \), and the following inequality holds:
$$\alpha(gx,gy) \psi \bigl( d(Tx,Ty) \bigr) \leq\theta \bigl( d(gx,gy) \bigr) - \varphi \bigl( d(gx,gy) \bigr)\quad \textit{for all }x,y\in X; $$ -
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that \(\alpha (gx_{0},Tx_{0})\geq1\) and T is \((d,g,\alpha)\)-right-continuous;
-
(b)
there exists \(x_{0}\in X\) such that \(\alpha (Tx_{0},gx_{0})\geq1\) and T is \((d,g,\alpha)\)-left-continuous.
-
(a)
Then T and g have, at least, a coincidence point.
Additionally, assume that T and g commute, \(\theta(0)=\varphi(0)\), \(\psi^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all coincidence points x and y of T and g, there exists \(z\in X\) such that z is, at the same time, \((g,\alpha )\)-comparable to x and to y.
Then T and g have a unique common fixed point \(\omega\in X\). Furthermore, \(\omega=gx\) for all \(x\in\operatorname{Coin}(T,g)\).
Proof
We only have to use \(\phi=\theta-\varphi\) in Corollary 4.1, because ϕ is upper semi-continuous from the right on \(( 0,\infty ) \). Moreover, for all \(t>0\), we have that
so \(\phi(t)<\psi(t)\) for all \(t>0\). □
Corollary 4.3
Corollary 4.2 also holds if we replace the third condition with the following one:
- (3′):
-
There exist three functions \(\psi\in{\mathcal{F}_{\mathrm{alt}}}\) and \(\theta,\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that θ is upper semi-continuous from the right on \(( 0,\infty ) \), φ is lower semi-continuous from the right on \(( 0,\infty ) \), \(\theta-\varphi<\psi\) on \(( 0,\infty ) \), and the following inequality holds:
$$\alpha(gx,gy) \psi \bigl( d(Tx,Ty) \bigr) \leq\theta \bigl( d(gx,gy) \bigr) - \varphi \bigl( d(gx,gy) \bigr) \quad \textit{for all }x,y\in X. $$
It is also interesting to highlight the case in which \(\theta=\psi\).
Corollary 4.4
Let \((X,d)\) be a metric space, let \(\alpha :X\times X\rightarrow{}[0,\infty)\) be a function, and let \(T,g:X\rightarrow X\) be two mappings such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\subseteq g(X)\) and \(( A,d ) \) is complete;
-
2.
α is g-transitive and T is \((g,\alpha)\)-admissible;
-
3.
There exist two functions \(\psi,\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that ψ is continuous and nondecreasing on \(( 0,\infty ) \), φ is lower semi-continuous from the right on \(( 0,\infty ) \), \(\varphi >0\) on \(( 0,\infty ) \), and the following inequality holds:
$$\alpha(gx,gy) \psi \bigl( d(Tx,Ty) \bigr) \leq\psi \bigl( d(gx,gy) \bigr) - \varphi \bigl( d(gx,gy) \bigr) \quad \textit{for all }x,y\in X; $$ -
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that \(\alpha (gx_{0},Tx_{0})\geq1\) and T is \((d,g,\alpha)\)-right-continuous;
-
(b)
there exists \(x_{0}\in X\) such that \(\alpha (Tx_{0},gx_{0})\geq1\) and T is \((d,g,\alpha)\)-left-continuous.
-
(a)
Then T and g have, at least, a coincidence point.
Additionally, assume that T and g commute, \(\psi(0)=\varphi(0)\), \(\psi^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all coincidence points x and y of T and g, there exists \(z\in X\) such that z is, at the same time, \((g,\alpha )\)-comparable to x and to y.
Then T and g have a unique common fixed point \(\omega\in X\). Furthermore, \(\omega=gx\) for all \(x\in\operatorname{Coin}(T,g)\).
If we use ψ as the identity mapping on \([0,\infty)\), we deduce the following statement.
Corollary 4.5
Corollary 4.4 remains true if we replace the third condition with the following one:
- (3′):
-
There exists a lower semi-continuous from the right on \(( 0,\infty ) \) function \(\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that \(\varphi>0\) on \(( 0,\infty ) \), and the following inequality holds:
$$\alpha(gx,gy) d(Tx,Ty)\leq d(gx,gy)-\varphi \bigl( d(gx,gy) \bigr)\quad \textit{for all }x,y\in X. $$
Furthermore, if \(\lambda\in [ 0,1 ) \) and we use \(\varphi (t)=(1-\lambda)t\) for all \(t\in [ 0,\infty ) \), then we derive the following result.
Corollary 4.6
Corollary 4.4 remains true if we replace the third condition with the following one:
- (3′′):
-
There exists \(\lambda\in [ 0,1 ) \) such that
$$\alpha(gx,gy) d(Tx,Ty)\leq\lambda d(gx,gy) \quad \textit{for all }x,y\in X. $$
In the following result, we use \(\alpha(x,y)=1\) for all \(x,y\in X\).
Corollary 4.7
Let \((X,d)\) be a metric space and let \(T,g:X\rightarrow X\) be two mappings such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\subseteq g(X)\) and \(( A,d ) \) is complete;
-
2.
There exists \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\) such that
$$\psi \bigl( d(Tx,Ty) \bigr) \leq\phi \bigl( d(gx,gy) \bigr)\quad \textit{for all }x,y\in X; $$ -
3.
T is \((d,g)\)-continuous.
Then T and g have, at least, a coincidence point.
Additionally, assume that T and g commute, \(\phi(0)=0\) and \(\psi ^{-1}(\{0\})=\{0\}\). Then T and g have a unique common fixed point \(\omega\in X\). Furthermore, \(\omega=gx\) for all \(x\in\operatorname{Coin}(T,g)\).
5 Some coincidence point theorems in metric spaces endowed with a binary relation
As we pointed out in Introduction, one of the branches that have attracted much attention in fixed point theory is dedicated to partially ordered metric spaces. However, some properties of a partial order are not necessary to prove some fixed/coincidence point theorem. In this section we show some consequences of our main results in the setting of metric spaces endowed with a binary relation which has only to be transitive on a subset of the metric space.
Definition 5.1
Let  be a binary relation on a set X and let A be a nonempty subset of X. We say that
be a binary relation on a set X and let A be a nonempty subset of X. We say that  is transitive on
A if
is transitive on
A if  for all \(a,b,c\in A\) such that
for all \(a,b,c\in A\) such that  and
and  .
.
Definition 5.2
Let \(( X,d ) \) be a metric space and let  be a binary relation on X. Given two mappings \(T,g:X\rightarrow X\) and a point \(z_{0}\in X\), we say that T is
be a binary relation on X. Given two mappings \(T,g:X\rightarrow X\) and a point \(z_{0}\in X\), we say that T is  -nondecreasing-continuous at
\(z_{0}\) is \(\{Tx_{n}\}\rightarrow Tz_{0}\) for all sequence \(\{x_{n}\}\subseteq X\) such that \(\{gx_{n}\}\rightarrow gz_{0}\) and
-nondecreasing-continuous at
\(z_{0}\) is \(\{Tx_{n}\}\rightarrow Tz_{0}\) for all sequence \(\{x_{n}\}\subseteq X\) such that \(\{gx_{n}\}\rightarrow gz_{0}\) and  for all \(n\in\mathbb{N}\). And T is
for all \(n\in\mathbb{N}\). And T is  -nondecreasing-continuous in
\(A\subseteq X\) if T is
-nondecreasing-continuous in
\(A\subseteq X\) if T is  -nondecreasing-continuous at every point of A.
-nondecreasing-continuous at every point of A.
Similarly, we say that T is  -nonincreasing-continuous at \(z_{0}\) is \(\{Tx_{n}\}\rightarrow Tz_{0}\) for all sequence \(\{x_{n}\}\subseteq X\) such that \(\{gx_{n}\}\rightarrow gz_{0}\) and
-nonincreasing-continuous at \(z_{0}\) is \(\{Tx_{n}\}\rightarrow Tz_{0}\) for all sequence \(\{x_{n}\}\subseteq X\) such that \(\{gx_{n}\}\rightarrow gz_{0}\) and  for all \(n\in\mathbb{N}\). And T is
for all \(n\in\mathbb{N}\). And T is  -nonincreasing-continuous in \(A\subseteq X\) if T is
-nonincreasing-continuous in \(A\subseteq X\) if T is  -nonincreasing-continuous at every point of A.
-nonincreasing-continuous at every point of A.
The following result directly follows from the respective definitions.
Lemma 5.1
Let
\(( X,d ) \)
be a metric space, let
\(T,g:X\rightarrow X\)
be two mappings, let
 be a binary relation on
X, and let
be a binary relation on
X, and let
 be the function defined in (2). Then the following properties hold.
be the function defined in (2). Then the following properties hold.
-
1.
Given \(z_{0}\in X\), the mapping T is
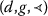 -nonincreasing-continuous at
\(z_{0}\)
if and only if it is
-nonincreasing-continuous at
\(z_{0}\)
if and only if it is
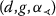 -right-continuous at
\(z_{0}\);
-right-continuous at
\(z_{0}\); -
2.
T is
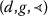 -nonincreasing-continuous if and only if
T
is
-nonincreasing-continuous if and only if
T
is
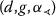 -right-continuous;
-right-continuous; -
3.
T is
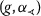 -admissible if and only if
T
is
-admissible if and only if
T
is
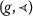 -nondecreasing;
-nondecreasing; -
4.
The binary relation
 is transitive on
\(g(X)\)
if and only if
is transitive on
\(g(X)\)
if and only if
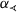 is
g-transitive.
is
g-transitive.
The main result of this section is the following one.
Theorem 5.1
Let
\((X,d)\)
be a metric space endowed with a binary relation
 and let
\(T,g:X\rightarrow X\)
be two mappings such that the following conditions are fulfilled:
and let
\(T,g:X\rightarrow X\)
be two mappings such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\subseteq g(X)\) and \(( A,d ) \) is complete;
-
2.
The binary relation
 is transitive on
\(g(X)\)
and
T
is
is transitive on
\(g(X)\)
and
T
is
 -nondecreasing;
-nondecreasing; -
3.
There exists \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\) such that
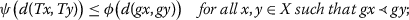
-
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that
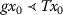 and
T
is
and
T
is
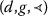 -nondecreasing-continuous;
-nondecreasing-continuous; -
(b)
there exists \(x_{0}\in X\) such that
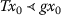 and
T
is
and
T
is
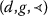 -nonincreasing-continuous.
-nonincreasing-continuous.
-
(a)
Then T and g have, at least, a coincidence point.
Additionally, assume that T and g commute, \(\phi(0)=0\), \(\psi ^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all coincidence points x and y of T and g, there exists \(z\in X\) such that gz is, at the same time,
 -comparable to
gx
and to
gy.
-comparable to
gx
and to
gy.
Then T and g have a unique common fixed point \(\omega\in X\). Furthermore, \(\omega=gx\) for all \(x\in\operatorname{Coin}(T,g)\).
Notice that, in the previous result, the binary relation  must only be transitive on \(g(X)\).
must only be transitive on \(g(X)\).
Proof
It follows from Theorems 3.1 and 3.3 using the function  defined in (2) and taking into account the equivalences given in Lemma 5.1. □
defined in (2) and taking into account the equivalences given in Lemma 5.1. □
We can repeat Corollaries 4.1-4.7 in this new framework. However, among them, we only highlight the following one.
Corollary 5.1
Let
\((X,d)\)
be a metric space endowed with a binary relation
 and let
\(T,g:X\rightarrow X\)
be two mappings such that the following conditions are fulfilled:
and let
\(T,g:X\rightarrow X\)
be two mappings such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\subseteq g(X)\) and \(( A,d ) \) is complete;
-
2.
The binary relation
 is transitive on
\(g(X)\)
and
T
is
is transitive on
\(g(X)\)
and
T
is
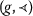 -nondecreasing;
-nondecreasing; -
3.
There exist three functions \(\psi,\theta,\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that ψ is continuous and nondecreasing on \(( 0,\infty ) \), θ is upper semi-continuous from the right on \(( 0,\infty ) \), φ is lower semi-continuous from the right on \(( 0,\infty ) \), \(\theta-\varphi<\psi\) on \(( 0,\infty ) \), and the following inequality holds:

-
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that
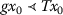 and
T
is
and
T
is
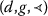 -nondecreasing-continuous;
-nondecreasing-continuous; -
(b)
there exists \(x_{0}\in X\) such that
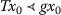 and
T
is
and
T
is
 -nonincreasing-continuous.
-nonincreasing-continuous.
-
(a)
Then T and g have, at least, a coincidence point.
Additionally, assume that T and g commute, \(\theta(0)=\varphi(0)\), \(\psi^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all coincidence points x and y of T and g, there exists \(z\in X\) such that gz is, at the same time,
 -comparable to
gx
and to
gy.
-comparable to
gx
and to
gy.
Then T and g have a unique common fixed point \(\omega\in X\). Furthermore, \(\omega=gx\) for all \(x\in\operatorname{Coin}(T,g)\).
Proof
It directly follows from Corollary 4.2 using the function  defined in (2). □
defined in (2). □
Corollary 5.2
Theorem
5.1
and Corollary
5.1
also hold if
 is a transitive relation on
X, or a preorder on
X, or a partial order on
X.
is a transitive relation on
X, or a preorder on
X, or a partial order on
X.
6 Fixed point theorems
If we use g as the identity mapping on X, we obtain the following fixed point theorems in metric spaces, endowed with a binary relation or not.
Theorem 6.1
Let \((X,d)\) be a metric space, let \(\alpha :X\times X\rightarrow{}[0,\infty)\) be a function and let \(T:X\rightarrow X\) be a mapping such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\) and \(( A,d ) \) is complete;
-
2.
α is transitive and T is α-admissible;
-
3.
There exists \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\) such that
$$\alpha(x,y) \psi \bigl( d(Tx,Ty) \bigr) \leq\phi \bigl( d(x,y) \bigr)\quad \textit{for all }x,y\in X; $$ -
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that \(\alpha(x_{0},Tx_{0})\geq 1\) and T is \((d,\alpha)\)-right-continuous;
-
(b)
there exists \(x_{0}\in X\) such that \(\alpha(Tx_{0},x_{0})\geq 1\) and T is \((d,\alpha)\)-left-continuous.
-
(a)
Then T has, at least, a fixed point.
Additionally, assume that \(\phi(0)=0\), \(\psi^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all fixed points x and y of T, there exists \(z\in X\) such that z is, at the same time, α-comparable to x and to y.
Then T has a unique fixed point.
Proof
It follows from Theorems 3.1 and 3.3 using g as the identity mapping on X. □
Corollary 6.1
Let \((X,d)\) be a metric space, let \(\alpha :X\times X\rightarrow{}[0,\infty)\) be a function and let \(T:X\rightarrow X\) be a mapping such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\) and \(( A,d ) \) is complete;
-
2.
α is transitive and T is α-admissible;
-
3.
There exist two functions \(\psi,\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that ψ is continuous and nondecreasing on \(( 0,\infty ) \), ϕ is upper semi-continuous from the right on \(( 0,\infty ) \), \(\phi<\psi\) on \(( 0,\infty ) \), and the following inequality holds:
$$\alpha(x,y) \psi \bigl( d(Tx,Ty) \bigr) \leq\phi \bigl( d(x,y) \bigr)\quad \textit{for all }x,y\in X; $$ -
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that \(\alpha(x_{0},Tx_{0})\geq 1\) and T is \((d,\alpha)\)-right-continuous;
-
(b)
there exists \(x_{0}\in X\) such that \(\alpha(Tx_{0},x_{0})\geq 1\) and T is \((d,\alpha)\)-left-continuous.
-
(a)
Then T has, at least, a fixed point.
Additionally, assume that \(\phi(0)=0\), \(\psi^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all fixed points x and y of T, there exists \(z\in X\) such that z is, at the same time, α-comparable to x and to y.
Then T has a unique fixed point.
Proof
It follows from Corollary 4.1 using g as the identity mapping on X. □
In the context of metric spaces that are not endowed with binary relations, we can also highlight the following statement, in which we assume that \(\alpha(x,y)=1\) for all \(x,y\in X\).
Corollary 6.2
Let \((X,d)\) be a complete metric space and let \(T:X\rightarrow X\) be a continuous mapping. Assume that there exist an altering distance function ψ, an upper semi-continuous from the right function \(\theta: [ 0,\infty ) \rightarrow [ 0,\infty ) \), and a lower semi-continuous from the right function \(\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that
where \(\theta(0)=\varphi(0)=0\) and \(\psi(t)-\theta(t)+\varphi(t)>0\) for all \(t>0\). Then T has a unique fixed point.
In the case of metric spaces endowed with binary relations, we have the following results.
Theorem 6.2
Let
\((X,d)\)
be a metric space endowed with binary relation
 and let
\(T:X\rightarrow X\)
be a mapping such that the following conditions are fulfilled:
and let
\(T:X\rightarrow X\)
be a mapping such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\) and \(( A,d ) \) is complete;
-
2.
The binary relation
 is transitive and
T
is
is transitive and
T
is
 -nondecreasing;
-nondecreasing; -
3.
There exists \(( \psi,\phi ) \in\mathcal{F}_{\mathcal{A}}\) such that
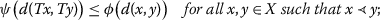
-
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that
 and
T
is
and
T
is
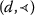 -nondecreasing-continuous;
-nondecreasing-continuous; -
(b)
there exists \(x_{0}\in X\) such that
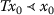 and
T
is
and
T
is
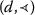 -nonincreasing-continuous.
-nonincreasing-continuous.
-
(a)
Then T has, at least, a fixed point.
Additionally, assume that \(\phi(0)=0\), \(\psi^{-1}(\{0\})=\{0\}\), and the following property holds:
-
(U)
For all fixed points x and y of T, there exists \(z\in X\) such that z is, at the same time,
 -comparable to
x
and to
y.
-comparable to
x
and to
y.
Then T has a unique fixed point.
Proof
It follows from Theorem 5.1 using g as the identity mapping on X. □
Corollary 6.3
Let
\((X,d)\)
be a metric space endowed with a binary relation
 and let
\(T:X\rightarrow X\)
be a mapping such that the following conditions are fulfilled:
and let
\(T:X\rightarrow X\)
be a mapping such that the following conditions are fulfilled:
-
1.
There exists a subset \(A\subseteq X\) such that \(T(X)\subseteq A\) and \(( A,d ) \) is complete;
-
2.
The binary relation
 is transitive and
T
is
is transitive and
T
is
 -nondecreasing;
-nondecreasing; -
3.
There exist three functions \(\psi,\theta,\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that ψ is continuous and nondecreasing on \(( 0,\infty ) \), θ is upper semi-continuous from the right on \(( 0,\infty ) \), φ is lower semi-continuous from the right on \(( 0,\infty ) \), \(\theta-\varphi<\psi\) on \(( 0,\infty ) \), and the following inequality holds:
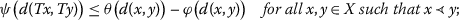
-
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that
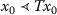 and
T
is
and
T
is
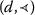 -nondecreasing-continuous;
-nondecreasing-continuous; -
(b)
there exists \(x_{0}\in X\) such that
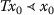 and
T
is
and
T
is
 -nonincreasing-continuous.
-nonincreasing-continuous.
-
(a)
Then T has, at least, a fixed point.
Additionally, assume that \(\theta(0)=\varphi(0)\), \(\psi^{-1}(\{0\})=\{ 0\}\), and the following property holds:
-
(U)
For all fixed points x and y of T, there exists \(z\in X\) such that z is, at the same time,
 -comparable to
x
and to
y.
-comparable to
x
and to
y.
Then T has a unique fixed point.
Proof
It follows from Corollary 5.1 using g as the identity mapping on X. □
7 A unified version of Ran and Reurings’ theorem and Nieto and Rodríguez-López’s theorem
After the appearance of Ran and Reurings’ theorem [17] and Nieto and Rodríguez-López’s theorem [18], many fixed point results were introduced in the ambient of metric spaces endowed with partial orders (see, for instance, [19] in which the authors introduced a close contractivity condition in L-spaces). Since them, many coincidence/fixed point theorems have been proved distinguishing between either the involved mappings are continuous or the ambient space is regular. In this section, we show a unified version of both theorems using a unique condition. The following one is the particularization of Definition 5.2 to the case in which g is the identity mapping on X and  is an arbitrary binary relation on X.
is an arbitrary binary relation on X.
Definition 7.1
Given a metric space \((X,d)\) endowed with a binary relation  , a mapping \(T:X\rightarrow X\) is
, a mapping \(T:X\rightarrow X\) is  -nondecreasing-continuous at
\(z_{0}\in X\) if we have that \(\{ Tx_{n}\}\) converges to \(Tz_{0}\) for all
-nondecreasing-continuous at
\(z_{0}\in X\) if we have that \(\{ Tx_{n}\}\) converges to \(Tz_{0}\) for all  -nondecreasing sequence \(\{ x_{n}\}\) convergent to \(z_{0}\). And T is
-nondecreasing sequence \(\{ x_{n}\}\) convergent to \(z_{0}\). And T is  -nondecreasing-continuous if it is
-nondecreasing-continuous if it is  -nondecreasing-continuous at every point of X.
-nondecreasing-continuous at every point of X.
Similarly, a mapping \(T:X\rightarrow X\) is  -nonincreasing-continuous at
\(z_{0}\in X\) if we have that \(\{Tx_{n}\}\) converges to \(Tz_{0}\) for all
-nonincreasing-continuous at
\(z_{0}\in X\) if we have that \(\{Tx_{n}\}\) converges to \(Tz_{0}\) for all  -nonincreasing sequence \(\{x_{n}\}\) convergent to \(z_{0}\). And T is
-nonincreasing sequence \(\{x_{n}\}\) convergent to \(z_{0}\). And T is  -nonincreasing-continuous if it is
-nonincreasing-continuous if it is  -nonincreasing-continuous at every point of X.
-nonincreasing-continuous at every point of X.
It is obvious that every continuous mapping is also nondecreasing-continuous, but the converse is false.
Example 7.1
If \(\mathbb{R}\) is endowed with the Euclidean metric (\(d_{e} ( x,y ) =\vert x-y\vert \) for all \(x,y\in\mathbb{R}\)) and its usual partial order ≤, then the mapping
is \(( d_{e},\leq ) \)-nondecreasing-continuous on \(\mathbb{R}\), but it is not continuous at \(x=0\).
The following one is a particularization of Corollary 6.3 using altering distance functions.
Theorem 7.1
Let
 be a metric space endowed with a transitive binary relation
be a metric space endowed with a transitive binary relation
 and let
\(T:X\rightarrow X\)
be a mapping such that the following conditions are fulfilled:
and let
\(T:X\rightarrow X\)
be a mapping such that the following conditions are fulfilled:
-
1.
\(( X,d ) \) (or \(( T(X),d ) \)) is complete;
-
2.
T is nondecreasing (w.r.t.
 );
); -
3.
There exist an altering distance function ψ and an upper semi-continuous from the right function \(\phi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that
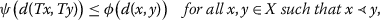
where \(\phi(0)=0\) and \(\phi(t)<\psi(t)\) for all \(t>0\);
-
4.
At least, one of the following conditions holds:
-
(a)
there exists \(x_{0}\in X\) such that
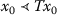 and
T
is
and
T
is
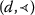 -nondecreasing-continuous;
-nondecreasing-continuous; -
(b)
there exists \(x_{0}\in X\) such that
 and
T
is
and
T
is
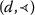 -nonincreasing-continuous;
-nonincreasing-continuous;
-
(a)
Then T has, at least, a fixed point.
Furthermore, assume that the following property holds:
-
(U)
For each \(x,y\in\operatorname{Fix}(T)\), there exists \(z\in X\) which is
 -comparable to
x
and
y.
-comparable to
x
and
y.
Then T has a unique fixed point.
The previous result improves Theorem 1.8 in three senses: (1) the binary relation  does not have to be a partial order, but a transitive binary relation; (2) ϕ has only to be upper semi-continuous from the right; (3) the mapping T must only be
does not have to be a partial order, but a transitive binary relation; (2) ϕ has only to be upper semi-continuous from the right; (3) the mapping T must only be  -nondecreasing-continuous, which is a condition that unifies and extends hypotheses 4(a) and 4(b) of Theorem 1.8.
-nondecreasing-continuous, which is a condition that unifies and extends hypotheses 4(a) and 4(b) of Theorem 1.8.
Theorem 7.2
Theorem 7.1 also holds if we replace assumption 3 with the following one:
-
1.
There exist an altering distance function ψ, an upper semi-continuous from the right function \(\theta: [ 0,\infty ) \rightarrow [ 0,\infty ) \), and a lower semi-continuous from the right function \(\varphi: [ 0,\infty ) \rightarrow [ 0,\infty ) \) such that
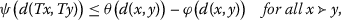 (8)
(8)where \(\theta(0)=\varphi(0)=0\) and \(\psi(t)-\theta(t)+\varphi(t)>0\) for all \(t>0\).
Corollary 7.1
Theorem 7.2 also holds if we replace assumption 4 with the following one:
- (3′):
-
There exists \(x_{0}\in X\) such that \(x_{0}\asymp Tx_{0}\) and T is continuous.
Proof
If follows from the fact that if T is continuous, then it is both  -nondecreasing-continuous and
-nondecreasing-continuous and  -nonincreasing-continuous. □
-nonincreasing-continuous. □
Corollary 7.2
Theorem 7.2 also holds if we replace assumption 4 with the following one:
- (3′′):
-
There exists \(x_{0}\in X\) such that \(x_{0}\asymp Tx_{0}\) and
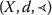 is regular.
is regular.
Proof
Following, point by point, the arguments of the proof of Theorem 3.1, we obtain that the Picard sequence \(\{ x_{n+1}=Tx_{n}\}\) is Cauchy and also it is  -monotone. As \((X,d)\) (or \((T(X),d)\)) is complete, there exists \(z\in X\) such that \(\{x_{n}\}\rightarrow z\). Since
-monotone. As \((X,d)\) (or \((T(X),d)\)) is complete, there exists \(z\in X\) such that \(\{x_{n}\}\rightarrow z\). Since  is regular, then
is regular, then

In any case, we can use the contractivity condition (8), which yields
for all \(n\in\mathbb{N}\). Assume, for n arbitrarily large, that \(x_{n}\ne z\). If \(d(x_{n+1}, Tz) >d(x_{n}, z)\) for some (large) n, then \(\psi(d(x_{n+1}, Tz))\geq\psi(d(x_{n}, z))>\theta(d(x_{n}, z))-\varphi(d(x_{n}, z))\), which contradicts (9). As a result, we have \(d(x_{n+1}, Tz) \leq d(x_{n}, z)\) for n arbitrarily large. On taking limit as \(n\to\infty\), we conclude that \(\{d(x_{n+1}, Tz)\}\to0\), that is, \(\{x_{n+1}\} \to Tz\). By the uniqueness of the limit, \(Tz=z\) and z is a fixed point of T. □
The following results are well known in the field of fixed point theory.
Corollary 7.3
(Ran and Reurings [17])
Let \((X,\preccurlyeq)\) be an ordered set endowed with a metric d and \(T:X\rightarrow X\) be a given mapping. Suppose that the following conditions hold:
-
(a)
\((X,d)\) is complete;
-
(b)
T is nondecreasing (w.r.t. ≼);
-
(c)
T is continuous;
-
(d)
There exists \(x_{0}\in X\) such that \(x_{0}\preccurlyeq Tx_{0}\);
-
(e)
There exists a constant \(\lambda\in(0,1)\) such that \(d(Tx,Ty)\leq \lambda d(x,y)\) for all \(x,y\in X\) with \(x\succcurlyeq y\).
Then T has a fixed point. Moreover, if for all \((x,y)\in X^{2}\) there exists \(z\in X\) such that \(x\preccurlyeq z\) and \(y\preccurlyeq z\), we obtain uniqueness of the fixed point.
Proof
It follows from Corollary 7.1. □
Corollary 7.4
(Nieto and Rodríguez-López [18])
Let \((X,\preccurlyeq)\) be an ordered set endowed with a metric d and \(T:X\rightarrow X\) be a given mapping. Suppose that the following conditions hold:
-
(a)
\((X,d)\) is complete;
-
(b)
T is nondecreasing (w.r.t. ≼);
-
(c)
If a nondecreasing sequence \(\{x_{m}\}\) in X converges to some point \(x\in X\), then \(x_{m}\preccurlyeq x\) for all m;
-
(d)
There exists \(x_{0}\in X\) such that \(x_{0}\preccurlyeq Tx_{0}\);
-
(e)
There exists a constant \(\lambda\in(0,1)\) such that \(d(Tx,Ty)\leq \lambda d(x,y)\) for all \(x,y\in X\) with \(x\succcurlyeq y\).
Then T has a fixed point. Moreover, if for all \((x,y)\in X^{2}\) there exists \(z\in X\) such that \(x\preccurlyeq z\) and \(y\preccurlyeq z\), we obtain uniqueness of the fixed point.
Proof
It follows from Corollary 7.2. □
Finally, we also prove that the Shaddad et al. theorem is an easy consequence of our main results.
Corollary 7.5
Theorem 1.8 immediately follows from Theorem 7.1.
Proof
It is only necessary to apply Corollaries 7.1 and 7.2 (which are immediate consequences of Theorem 7.1), which cover cases 4(a) and 4(b) in Theorem 1.8. □
Finally, we point out that the present techniques can be easily generalized to guarantee the existence and uniqueness of multidimensional coincidence/fixed points following the techniques described in [20–26].
References
Dutta, PN, Choudhury, BS: A generalization of contraction principle in metric spaces. Fixed Point Theory Appl. 2008, Article ID 406368 (2008)
Khan, MS, Swaleh, M, Sessa, S: Fixed point theorems by altering distances between the points. Bull. Aust. Math. Soc. 30(1), 1-9 (1984)
Abbas, M, Đorić, D: Common fixed point theorem for four mappings satisfying generalized weak contractive condition. Filomat 24(2), 1-10 (2010)
Đorić, D: Common fixed point for generalized \((\psi,\phi)\)-weak contractions. Appl. Math. Lett. 22, 1896-1900 (2009)
Harjani, J, Sadarangani, K: Generalized contractions in partially ordered metric spaces and applications to ordinary differential equations. Nonlinear Anal. 72, 1188-1197 (2010)
Eslamian, M, Abkar, A: A fixed point theorem for generalized weakly contractive mappings in complete metric space. Ital. J. Pure Appl. Math. (in press)
Aydi, H, Karapınar, E, Samet, B: Remarks on some recent fixed point theorems. Fixed Point Theory Appl. 2012, Article ID 76 (2012)
Choudhury, BS, Kundu, A: A coupled coincidence point result in partially ordered metric spaces for compatible mappings. Nonlinear Anal. 73, 2524-2531 (2010)
Shaddad, F, Noorani, MSM, Alsulami, SM, Akhadkulov, H: Coupled point results in partially ordered metric spaces without compatibility. Fixed Point Theory Appl. 2014, Article ID 204 (2014)
Razani, A, Parvaneh, V: Coupled coincidence point results for \(( \psi,\alpha,\beta ) \)-weak contractions in partially ordered metric spaces. J. Appl. Math. 2012, Article ID 496103 (2012)
Schweizer, B, Sklar, A: Probabilistic Metric Spaces. Dover, New York (2005)
Ding, H-S, Karapınar, E: Meir Keeler type contractions in partially ordered G-metric space. Fixed Point Theory Appl. 2013, Article ID 35 (2013)
Roldán, A, Martínez-Moreno, J, Roldán, C: Multidimensional fixed point theorems in partially ordered complete metric spaces. J. Math. Anal. Appl. 396(2), 536-545 (2012)
Berzig, M, Karapınar, E, Roldán, A: Discussion on generalized-\((\alpha\psi,\beta\varphi)\)-contractive mappings via generalized altering distance function and related fixed point theorems. Abstr. Appl. Anal. 2014, Article ID 259768 (2014)
Roldán, A, Karapınar, E: Some multidimensional fixed point theorems on partially preordered \(G^{\ast}\)-metric spaces under \((\psi,\phi)\)-contractivity conditions. Fixed Point Theory Appl. 2013, Article ID 158 (2013)
Roldán, A, Martínez-Moreno, J, Roldán, C, Karapınar, E: Multidimensional fixed point theorems in partially ordered complete partial metric spaces under \((\psi,\varphi)\)-contractivity conditions. Abstr. Appl. Anal. 2013, Article ID 634371 (2013)
Ran, ACM, Reurings, MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proc. Am. Math. Soc. 132, 1435-1443 (2004)
Nieto, JJ, Rodríguez-López, R: Contractive mapping theorem in partially ordered sets and applications to ordinary differential equations. Order 22, 223-239 (2005)
Petrusel, A, Rus, IA: Fixed point theorems in ordered L-spaces. Proc. Am. Math. Soc. 134, 411-418 (2006)
Roldán, A, Martínez-Moreno, J, Roldán, C, Karapınar, E: Meir-Keeler type multidimensional fixed point theorems in partially ordered complete metric spaces. Abstr. Appl. Anal. 2013, Article ID 406026 (2013)
Karapınar, E, Roldán, A: A note on ‘n-tuplet fixed point theorems for contractive type mappings in partially ordered metric spaces’. J. Inequal. Appl. 2013, Article ID 567 (2013)
Karapınar, E, Roldán, A, Shahzad, N, Sintunaravat, W: Discussion of coupled and tripled coincidence point theorems for φ-contractive mappings without the mixed g-monotone property. Fixed Point Theory Appl. 2014, Article ID 92 (2014)
Al-Mezel, SA, Alsulami, HH, Karapınar, E, Roldán, A: Discussion on ‘multidimensional coincidence points’ via recent publications. Abstr. Appl. Anal. 2014, Article ID 287492 (2014)
Roldán-López-de-Hierro, AF, Karapınar, E, de la Sen, M: Coincidence point theorems in quasi-metric spaces without assuming the mixed monotone property and consequences in G-metric spaces. Fixed Point Theory Appl. 2014, Article ID 184 (2014)
Roldán, A, Martínez-Moreno, J, Roldán, C, Karapınar, E: Some remarks on multidimensional fixed point theorems. Fixed Point Theory 15, 545-558 (2014)
Roldán, A, Martínez-Moreno, J, Roldán, C, Cho, YJ: Multidimensional fixed point theorems under \(( \psi ,\varphi ) \)-contractive conditions in partially ordered complete metric spaces. J. Comput. Appl. Math. 273, 76-87 (2015)
Acknowledgements
This article was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah. N Shahzad acknowledges with thanks DSR for financial support. A-F Roldán-López-de-Hierro is grateful to the Department of Quantitative Methods for Economics and Business of the University of Granada. The same author has been partially supported by Junta de Andalucía by project FQM-268 of the Andalusian CICYE.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this article. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Shahzad, N., Karapınar, E. & Roldán-López-de-Hierro, AF. On some fixed point theorems under \((\alpha,\psi,\phi)\)-contractivity conditions in metric spaces endowed with transitive binary relations. Fixed Point Theory Appl 2015, 124 (2015). https://doi.org/10.1186/s13663-015-0359-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/s13663-015-0359-5
 for all
for all  for all
for all 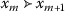 for all
for all 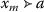 for all
for all  is transitive if, and only if,
is transitive if, and only if,  is transitive.
is transitive. -nondecreasing if, and only if, T is
-nondecreasing if, and only if, T is  -admissible.
-admissible.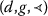 -nonincreasing-continuous at
-nonincreasing-continuous at
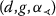 -right-continuous at
-right-continuous at
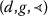 -nonincreasing-continuous if and only if
T
is
-nonincreasing-continuous if and only if
T
is
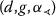 -right-continuous;
-right-continuous;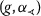 -admissible if and only if
T
is
-admissible if and only if
T
is
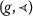 -nondecreasing;
-nondecreasing; is transitive on
is transitive on
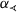 is
g-transitive.
is
g-transitive. is transitive on
is transitive on
 -nondecreasing;
-nondecreasing;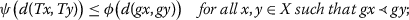
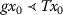 and
T
is
and
T
is
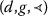 -nondecreasing-continuous;
-nondecreasing-continuous;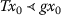 and
T
is
and
T
is
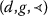 -nonincreasing-continuous.
-nonincreasing-continuous. -comparable to
gx
and to
gy.
-comparable to
gx
and to
gy. is transitive on
is transitive on
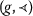 -nondecreasing;
-nondecreasing;
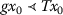 and
T
is
and
T
is
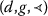 -nondecreasing-continuous;
-nondecreasing-continuous;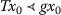 and
T
is
and
T
is
 -nonincreasing-continuous.
-nonincreasing-continuous. -comparable to
gx
and to
gy.
-comparable to
gx
and to
gy. is transitive and
T
is
is transitive and
T
is
 -nondecreasing;
-nondecreasing;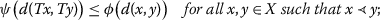
 and
T
is
and
T
is
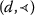 -nondecreasing-continuous;
-nondecreasing-continuous;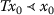 and
T
is
and
T
is
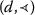 -nonincreasing-continuous.
-nonincreasing-continuous. -comparable to
x
and to
y.
-comparable to
x
and to
y. is transitive and
T
is
is transitive and
T
is
 -nondecreasing;
-nondecreasing;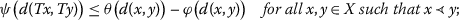
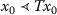 and
T
is
and
T
is
 -nondecreasing-continuous;
-nondecreasing-continuous;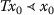 and
T
is
and
T
is
 -nonincreasing-continuous.
-nonincreasing-continuous. -comparable to
x
and to
y.
-comparable to
x
and to
y. );
);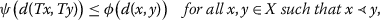
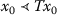 and
T
is
and
T
is
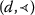 -nondecreasing-continuous;
-nondecreasing-continuous; and
T
is
and
T
is
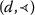 -nonincreasing-continuous;
-nonincreasing-continuous; -comparable to
x
and
y.
-comparable to
x
and
y.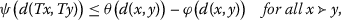
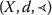 is regular.
is regular.