- Research
- Open access
- Published:
A simultaneous iterative method for split equality problems of two finitefamilies of strictly pseudononspreading mappings without prior knowledge ofoperator norms
Fixed Point Theory and Applications volume 2015, Article number: 1 (2015)
Abstract
In this article, we first introduce the concept of T-mapping of a finitefamily of strictly pseudononspreading mapping  , and we show that the fixed point set of theT-mapping is the set of common fixed points of
, and we show that the fixed point set of theT-mapping is the set of common fixed points of and T is a quasi-nonexpansive mapping.Based on the concept of a T-mapping, we propose a simultaneousiterative algorithm to solve the split equality problem with a way of selectingthe stepsizes which does not need any prior information about the operatornorms. The sequences generated by the algorithm weakly converge to a solution ofthe split equality problem of two finite families of strictly pseudononspreadingmappings. Furthermore, we apply our iterative algorithms to some convex andnonlinear problems.
and T is a quasi-nonexpansive mapping.Based on the concept of a T-mapping, we propose a simultaneousiterative algorithm to solve the split equality problem with a way of selectingthe stepsizes which does not need any prior information about the operatornorms. The sequences generated by the algorithm weakly converge to a solution ofthe split equality problem of two finite families of strictly pseudononspreadingmappings. Furthermore, we apply our iterative algorithms to some convex andnonlinear problems.
MSC: 47H09, 47H05, 47H06, 47J25.
1 Introduction
Due to their extraordinary utility and broad applicability in many areas of appliedmathematics (most notably, fully discretized models of problems in imagereconstruction from projections, in image processing, and in intensity-modulatedradiation therapy), algorithms for solving convex feasibility problems continue toreceive great attention; see for instance [1–11]. Recently, Moudafi [12] introduced a new convex feasibility problem (CFP). Let ,
,  ,
,  be real Hilbert spaces, let
be real Hilbert spaces, let  ,
,  be two nonempty closed convex sets, let
be two nonempty closed convex sets, let ,
,  be two bounded linear operators. The convexfeasibility problem in [12] is to find
be two bounded linear operators. The convexfeasibility problem in [12] is to find

which allows asymmetric and partial relations between the variables x andy. The interest is to cover many situations, for instance indecomposition methods for PDEs, applications in game theory and inintensity-modulated radiation therapy (IMRT). In decision sciences, this allows oneto consider agents who interplay only via some components of their decisionvariables, for further details, the interested reader is referred to [13]. In IMRT, this amounts to envisage a weak coupling between the vector ofdoses absorbed in all voxels and that of the radiation intensity, for furtherdetails, the interested reader is referred to [13, 14].
For solving the CFP (1.1), Moudafi [12] studied the fixed point formulation of the solutions of the CFP (1.1).Assume that the CFP (1.1) is consistent (i.e., (1.1) has a solution), if solves (1.1), then it solves the following fixedpoint equation system:
solves (1.1), then it solves the following fixedpoint equation system:

where  are any positive constants, and then Moudafiintroduced the following alternating CQ algorithm:
are any positive constants, and then Moudafiintroduced the following alternating CQ algorithm:

where  ,
,  and
and  are the spectral radii of
are the spectral radii of  and
and  , respectively. The weak convergence of the sequence
, respectively. The weak convergence of the sequence to a solution of (1.1) under some conditions wasproved.
to a solution of (1.1) under some conditions wasproved.
In [15], Moudafi and Al-Shemas considered the following problem:

and proposed the following simultaneous algorithm:

for firmly quasi-nonexpansive operators U and T, where ,
,  and
and  are the spectral radiuses of
are the spectral radiuses of  and
and  , respectively.
, respectively.
Observe that in the algorithms (1.3) and (1.5) mentioned above, the determination ofthe stepsize  depends on the operator (matrix) norms
depends on the operator (matrix) norms and
and  (or the largest eigenvalues of
(or the largest eigenvalues of and
and  ). To implement the alternating algorithm (1.3) andthe simultaneous algorithm (1.5), one has first to compute (or, at least, estimate)operator norms of A and B, which is in general not easy inpractice.
). To implement the alternating algorithm (1.3) andthe simultaneous algorithm (1.5), one has first to compute (or, at least, estimate)operator norms of A and B, which is in general not easy inpractice.
To overcome this difficulty, Lopez et al.[16] and Zhao et al.[17] presented useful method for choosing the stepsizes which do not needprior knowledge of the operator norms for solving the split feasibility problems andmultiple-set split feasibility problems, respectively.
Motivated by above results, we introduce a new choice of the stepsize sequence for the simultaneous iterative algorithm to solve(1.4) governed by quasi-nonexpansive mapping as follows:
for the simultaneous iterative algorithm to solve(1.4) governed by quasi-nonexpansive mapping as follows:

The advantage of our choice (1.6) of the stepsizes lies in the fact that no priorinformation about the operator norms of A and B is required, andstill convergence is guaranteed.
In this article, we propose the following simultaneous iterative algorithm where thestepsizes do not depend on the operator norms  and
and  and prove the weak convergence of the algorithm tosolve (1.4). Let
and prove the weak convergence of the algorithm tosolve (1.4). Let  and
and  be two quasi-nonexpansive mappings which are definedby (2.5). We denote by Γ be the set of solutions of (1.4), i.e.,
be two quasi-nonexpansive mappings which are definedby (2.5). We denote by Γ be the set of solutions of (1.4), i.e.,

Algorithm 1.1 Let  ,
,  be arbitrary and
be arbitrary and  be real number sequences in
be real number sequences in  . Assume that the kth iterate
. Assume that the kth iterate ,
,  has been constructed and
has been constructed and  , then we calculate
, then we calculate  th iterate
th iterate  via the formula
via the formula

where the stepsize  is chosen by (1.6). If
is chosen by (1.6). If  , then
, then  is a solution of the problem (1.4) and the iterativeprocess stops. Otherwise, we set
is a solution of the problem (1.4) and the iterativeprocess stops. Otherwise, we set  and go on to (1.7) to evaluate the next iterate
and go on to (1.7) to evaluate the next iterate .
.
Remark 1.1 Notice that in (1.6) the choice of the stepsize is independent of the norms
is independent of the norms  and
and  .
.
2 Preliminaries
Throughout this paper, we denote by H be a real Hilbert space with innerproduct  and induced norm
and induced norm  , and denote by C be a nonempty closed convexsubset of H. Let
, and denote by C be a nonempty closed convexsubset of H. Let  be a mapping. A point
be a mapping. A point  is said to be a fixed point of T provided
is said to be a fixed point of T provided . we use
. we use  to denote the fixed point set. We write
to denote the fixed point set. We write to indicate that the sequence
to indicate that the sequence  converges weakly to x,
converges weakly to x, implies that
implies that  converges strongly to x. We use
converges strongly to x. We use to stand for the weak ω-limit set of
to stand for the weak ω-limit set of . For any
. For any  , there exists a unique nearest point in C,denoted by
, there exists a unique nearest point in C,denoted by  , such that
, such that

Before proceeding, we need to introduce a few concepts.
A mapping  belongs to the set
belongs to the set  of quasi-nonexpansive, if
of quasi-nonexpansive, if

A mapping  belongs to the set
belongs to the set  of nonexpansive, if
of nonexpansive, if

A mapping  belongs to the set
belongs to the set  of firmly nonexpansive, if
of firmly nonexpansive, if

A mapping  belongs to the set
belongs to the set  of firmly quasi-nonexpansive, if
of firmly quasi-nonexpansive, if

A mapping  is called nonspreading, if
is called nonspreading, if

A mapping  is called k-strictly pseudononspreading ifthere exists
is called k-strictly pseudononspreading ifthere exists  such that
such that

Remark 2.1 It is easy to see that  and
and  . Furthermore,
. Furthermore,  is well known to contain resolvents and projectionoperators, and
is well known to contain resolvents and projectionoperators, and  includes subgradient projection operators [18]. T is a nonspreading mapping if and only if T is a0-strictly pseudononspreading mapping.
includes subgradient projection operators [18]. T is a nonspreading mapping if and only if T is a0-strictly pseudononspreading mapping.
The so-called demiclosedness principle plays an important role in our argument.
A mapping  is called demiclosed at the origin if for anysequence
is called demiclosed at the origin if for anysequence  which weakly converges to x, and if thesequence
which weakly converges to x, and if thesequence  strongly converges to 0, then
strongly converges to 0, then  .
.
To establish our results, we need the following technical lemmas.
Lemma 2.1 ([19])
If , then:
, then:
-
(a)
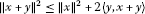 .
. -
(b)
For any
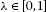 ,
, 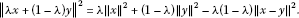
-
(c)
For
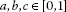 with
with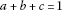 ,
, 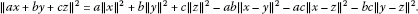
The following definition will be useful for our results.
In 2009, Kangtunyakarn and Suantai [20] introduced T-mapping generated by  and
and  as follows.
as follows.
Definition 2.1 Let C be a nonempty convex subset of real Banachspace. Let  be a finite family of mappings of C intoitself, and let
be a finite family of mappings of C intoitself, and let  be real numbers such that
be real numbers such that  for every
for every  . We define a mapping
. We define a mapping  as follows:
as follows:

Such a mapping T is called the T-mapping generated by and
and  .
.
Using the above definition, we have the following important lemma.
Lemma 2.2LetCbe a nonempty convex subset of real Banach space. Let be a finite family of
be a finite family of -strictly pseudononspreading mappings ofCinto itself with
-strictly pseudononspreading mappings ofCinto itself with , and let
, and let be real numbers such that
be real numbers such that for every
for every . IfTis theT-mapping generated by
. IfTis theT-mapping generated by and
and , then
, then andTis a quasi-nonexpansive mapping.
andTis a quasi-nonexpansive mapping.
Proof It is easy to deduce that  . Next, we claim that
. Next, we claim that  . Let
. Let  and
and  . Assume that
. Assume that  , for
, for  , it follows from
, it follows from  being a finite family of
being a finite family of  -strictly pseudononspreading mappings of Cinto itself that
-strictly pseudononspreading mappings of Cinto itself that

From the definition of T and (2.6), we have

which means  , that is,
, that is,  . Furthermore,
. Furthermore,

it yields  . Applying the same argument, we can conclude that
. Applying the same argument, we can conclude that and
and  , for
, for  .
.
Next, we claim that  . Indeed,
. Indeed,

It follows that  . Therefore,
. Therefore,  , that is,
, that is,  . Hence,
. Hence,  . From the definition of T and (2.7), we findthat T is a quasi-nonexpansive mapping. □
. From the definition of T and (2.7), we findthat T is a quasi-nonexpansive mapping. □
Proposition 2.1LetCbe a closed convex subset of a real Hilbert spaceH. IfTis a quasi-nonexpansive mapping fromCinto itself, then is closed and convex.
is closed and convex.
Proof Obviously, the continuity of T implies that is closed. Now, we show that
is closed. Now, we show that  is convex. For
is convex. For  and
and  , put
, put  . Now, we claim that
. Now, we claim that  . In fact,
. In fact,

which means that  . Hence,
. Hence,  and
and  is convex. □
is convex. □
3 Main results
Now, we are in a position to prove our convergence results in this section.
Theorem 3.1Let ,
,  ,
,  be real Hilbert spaces. Given two bounded linear operators
be real Hilbert spaces. Given two bounded linear operators ,
,  . Let
. Let be a finite family of
be a finite family of -strictly pseudononspreading mappings ofCinto itself with
-strictly pseudononspreading mappings ofCinto itself with , and Let
, and Let be a finite family of
be a finite family of -strictly pseudononspreading mappings ofQinto itself with
-strictly pseudononspreading mappings ofQinto itself with . Suppose thatUis defined by (2.5) which is generated by
. Suppose thatUis defined by (2.5) which is generated by and
and , with
, with for every
for every , and suppose thatTis defined by (2.5) which is generated by
, and suppose thatTis defined by (2.5) which is generated by and
and , with
, with for every
for every , respectively. Assume that
, respectively. Assume that and
and are demiclosed at the origin. If the solution set Γof (1.4) is nonempty and for small enough
are demiclosed at the origin. If the solution set Γof (1.4) is nonempty and for small enough and
and ,
,

then the sequence generated by Algorithm 1.1 weakly converges to a solution
generated by Algorithm 1.1 weakly converges to a solution of (1.4). Moreover,
of (1.4). Moreover,  ,
,  , and
, and as
as .
.
Proof It follows from the condition on  that
that

and

On the other hand, from

and

we obtain  and
and  . Furthermore,
. Furthermore,

Inequalities (3.1) and (3.2) lead to  and
and  is bounded.
is bounded.
For  , by Algorithm 1.1, we obtain
, by Algorithm 1.1, we obtain

Notice that

Substituting (3.4) into (3.3), one has

Similarly, by Algorithm 1.1, we deduce

Furthermore, adding the two last inequalities, following from the fact , we have
, we have

Next, we will estimate  and
and  . It follows from U and T being twoquasi-nonexpansive mappings that
. It follows from U and T being twoquasi-nonexpansive mappings that

and

Thus, (3.8) and (3.9) lead to

Furthermore, it follows from (3.7) that

Now, setting  , one has
, one has

On the other hand, note that

From the assumptions on  and
and  , we see that the sequence
, we see that the sequence  being decreasing and lower bounded by 0,consequently, converges to some finite limit, that is,
being decreasing and lower bounded by 0,consequently, converges to some finite limit, that is,  , which means the sequences
, which means the sequences  and
and  are bounded. Thus, we have
are bounded. Thus, we have


and

Now, we show that  . Indeed, as is shown below, we break up the proof bydistinguishing two cases.
. Indeed, as is shown below, we break up the proof bydistinguishing two cases.
Case 1. Suppose that there exists  such that
such that  , for all
, for all  , we obtain
, we obtain  . It yields
. It yields

Furthermore, (3.13) leads to

Since

and

we deduce

Conversely, suppose that there exists  such that
such that  , for all
, for all  , following the above process, we obtain theresults.
, following the above process, we obtain theresults.
Case 2. Suppose that there does not exist  such that
such that

or

for all  . We can divide the sequence
. We can divide the sequence  into two sequences: one satisfies
into two sequences: one satisfies , which is denoted by
, which is denoted by  and the other sequence satisfies
and the other sequence satisfies , which is denoted by
, which is denoted by  . Following the process of Case 1, we show that theresults hold for the subsequences with
. Following the process of Case 1, we show that theresults hold for the subsequences with  and
and  . Thus, we obtain
. Thus, we obtain  .
.
Let us prove that  and
and  are asymptotically regular. Indeed, since
are asymptotically regular. Indeed, since

one has

Consequently,

which yields  is asymptotically regular. Similarly,
is asymptotically regular. Similarly, and
and  is asymptotically regular, too.
is asymptotically regular, too.
Next, we show that  and
and  as
as  . Indeed, since
. Indeed, since

(3.15) and (3.17) mean that  . In the same way as above, we can also show that
. In the same way as above, we can also show that as
as  .
.
Taking  , from
, from  and
and  , we obtain
, we obtain  and
and  . Combining with the demiclosednesses of
. Combining with the demiclosednesses of and
and  at 0, one has
at 0, one has

which yields  and
and  . Thus,
. Thus,  and
and  . On the other hand,
. On the other hand,  and lower semicontinuity of the norm imply that
and lower semicontinuity of the norm imply that

hence  .
.
Finally, we will show the uniqueness of the weak cluster points of and
and  . Indeed, let
. Indeed, let  ,
,  be other weak cluster points of
be other weak cluster points of and
and  , respectively. From the definition of
, respectively. From the definition of , we have
, we have

Without loss of generality, we may assume that  ,
,  , and then
, and then

Reversing the role of  and
and  , we obtain
, we obtain

Equations (3.19) and (3.20) yield

which means  and
and  . Hence, the sequence
. Hence, the sequence  weakly converges to a solution of the problem (1.4),which completes the proof. □
weakly converges to a solution of the problem (1.4),which completes the proof. □
The following conclusions can be obtained from Theorem 3.1 immediately.
Theorem 3.2Let ,
,  ,
,  be real Hilbert spaces. Given two bounded linear operators
be real Hilbert spaces. Given two bounded linear operators ,
,  . LetUbe aρ-strictly pseudononspreading mapping ofCinto itself and LetTbe aτ-strictly pseudononspreading mapping ofQinto itself. Assume that
. LetUbe aρ-strictly pseudononspreading mapping ofCinto itself and LetTbe aτ-strictly pseudononspreading mapping ofQinto itself. Assume that and
and are demiclosed at the origin. If the solution set Γof (1.4) is nonempty and for small enough
are demiclosed at the origin. If the solution set Γof (1.4) is nonempty and for small enough and
and ,
,

then the sequence generated by Algorithm 1.1 weakly converges to a solution
generated by Algorithm 1.1 weakly converges to a solution of (1.4). Moreover,
of (1.4). Moreover,  ,
,  , and
, and as
as .
.
Theorem 3.3Let ,
,  ,
,  be real Hilbert spaces. Given two bounded linear operators
be real Hilbert spaces. Given two bounded linear operators ,
,  . LetUbe a nonspreading mapping ofCinto itself and letTbe a nonspreading mapping ofQinto itself. Assume that
. LetUbe a nonspreading mapping ofCinto itself and letTbe a nonspreading mapping ofQinto itself. Assume that and
and are demiclosed at the origin. If the solution set Γof (1.4) is nonempty and for small enough
are demiclosed at the origin. If the solution set Γof (1.4) is nonempty and for small enough and
and ,
,

then the sequence generated by Algorithm 1.1 weakly converges to a solution
generated by Algorithm 1.1 weakly converges to a solution of (1.4). Moreover,
of (1.4). Moreover,  ,
,  , and
, and as
as .
.
4 Applications
We now pay attention to applying our simultaneous iterative algorithms to some convexand nonlinear analysis notions; see, for example, [21].
4.1 Split feasibility problem
Let C and Q be nonempty closed convex subset of real Hilbertspaces  and
and  , respectively. The split feasibility problem(SFP) is to find a point
, respectively. The split feasibility problem(SFP) is to find a point

where  is a bounded linear operator. The SFP was firstintroduced by Censor and Elfving [22] for modeling inverse problems which arise from phase retrievals andin medical image reconstruction [23].
is a bounded linear operator. The SFP was firstintroduced by Censor and Elfving [22] for modeling inverse problems which arise from phase retrievals andin medical image reconstruction [23].
If  ,
,  , then Algorithm 1.1 becomes:
, then Algorithm 1.1 becomes:
Algorithm 4.1

where the stepsize  is chosen by (1.6). If
is chosen by (1.6). If  , then
, then  is a solution of the problem (4.1) and theiterative process stops. Otherwise, we set
is a solution of the problem (4.1) and theiterative process stops. Otherwise, we set  and go on to (4.1) to evaluate the next iterate
and go on to (4.1) to evaluate the next iterate .
.
Furthermore, if  and
and  , then we obtain the following simultaneousiterative algorithm for solving SFP (4.1).
, then we obtain the following simultaneousiterative algorithm for solving SFP (4.1).
Algorithm 4.2

where the stepsize  is chosen by (1.6). If
is chosen by (1.6). If  , then
, then  is a solution of the problem (4.1) and theiterative process stops. Otherwise, we set
is a solution of the problem (4.1) and theiterative process stops. Otherwise, we set  and go on to (4.3) to evaluate the next iterate
and go on to (4.3) to evaluate the next iterate .
.
4.2 Variational problems via resolvent mappings
Given a maximal monotone operator  , it is well known that its associated resolventmapping,
, it is well known that its associated resolventmapping,  , is quasi-nonexpansive and
, is quasi-nonexpansive and , which implies that zeroes of M areexactly fixed points of its resolvent mapping. If
, which implies that zeroes of M areexactly fixed points of its resolvent mapping. If  and
and  , where
, where  is another maximal monotone operator, the problemunder consideration is nothing but
is another maximal monotone operator, the problemunder consideration is nothing but

and the algorithm is applied to the following form.
Algorithm 4.3

where the stepsize  is chosen by (1.6). If
is chosen by (1.6). If  , then
, then  is a solution of the problem (4.4) and theiterative process stops. Otherwise, we set
is a solution of the problem (4.4) and theiterative process stops. Otherwise, we set  and go on to (4.5) to evaluate the next iterate
and go on to (4.5) to evaluate the next iterate .
.
References
Aleyner A, Reich S: Block-iterative algorithms for solving convex feasibility problems in Hilbertand in Banach spaces.J. Math. Anal. Appl. 2008,343(1):427–435. 10.1016/j.jmaa.2008.01.087
Bauschke HH, Borwein JM: On projection algorithms for solving convex feasibility problems.SIAM Rev. 1996,38(3):367–426. 10.1137/S0036144593251710
Byrne C: A Unified Treatment of Some Iterative Algorithms in Signal Processing andImage Reconstruction. Dekker, New York; 1984.
Masad E, Reich S: A note on the multiple-set split convex feasibility problem in Hilbertspace.J. Nonlinear Convex Anal. 2007, 8:367–371.
Yao Y, Chen R, Marino G, Liou YC: Applications of fixed point and optimization methods to the multiple-setssplit feasibility problem.J. Appl. Math. 2012., 2012: Article ID 927530
Qu B, Xiu N: A note on the CQ algorithm for the split feasibility problem.Inverse Probl. 2005, 21:1655–1665. 10.1088/0266-5611/21/5/009
Qu B, Xiu N: A new halfspace-relaxation projection method for the split feasibilityproblem.Linear Algebra Appl. 2008,428(5):1218–1229.
Xu HK: Iterative methods for the split feasibility problem in infinite-dimensionalHilbert spaces.Inverse Probl. 2010,26(10):5018–5034.
Censor Y, Elfving T, Kopf N, Bortfled T: The multi-sets split feasibility problem and it applications to inverseproblems.Inverse Probl. 2005, 21:2071–2084. 10.1088/0266-5611/21/6/017
Yang Q: The relaxed CQ algorithm for solving the split feasibility problem.Inverse Probl. 2004, 20:1261–1266. 10.1088/0266-5611/20/4/014
Zhao J, Yang Q: Several solution methods for the split feasibility problem.Inverse Probl. 2005, 21:1791–1799. 10.1088/0266-5611/21/5/017
Moudafi A: Alternating CQ-algorithm for convex feasibility and split fixed-pointproblems.J. Nonlinear Convex Anal. 2014, 15:809–818.
Attouch H, Bolte J, Redont P, Soubeyran A: Alternating proximal algorithms for weakly coupled minimization problems.Applications to dynamical games and PDEs.J. Convex Anal. 2008, 15:485–506.
Censor Y, Bortfeld T, Martin B, Trofimov A: A unified approach for inversion problems in intensity-modulated radiationtherapy.Phys. Med. Biol. 2006, 51:2353–2365. 10.1088/0031-9155/51/10/001
Moudafi A, Al-Shemas E: Simultaneous iterative methods for split equality problems andapplications.Trans. Math. Program. Appl. 2013, 1:1–11.
Lopez G, Martin-Marquez V, Wang F, Xu H: Solving the split feasibility problem without prior knowledge of matrixnorms.Inverse Probl. 2012., 27: Article ID 085004
Zhao J, Zhang J, Yang Q: A simple projection method for solving the multiple-sets split feasibilityproblem.Inverse Probl. Sci. Eng. 2013, 21:537–546. 10.1080/17415977.2012.712521
Maruster S, Popirlan C: On the Mann-type iteration and convex feasibility problem.J. Comput. Appl. Math. 2008, 24:390–396.
Chang SS: Some problems and results in the study of nonlinear analysis.Nonlinear Anal. 1997,30(7):4197–4208. 10.1016/S0362-546X(97)00388-X
Kangtunyakarn A, Suantai S: A new mapping for finding common solutions of equilibrium problems and fixedpoint problems of finite family of nonexpansive mappings.Nonlinear Anal. 2009, 71:4448–4460. 10.1016/j.na.2009.03.003
Rockafellar RT, Wets R Grundlehren der Mathematischen Wissenschafte 317. In Variational Analysis. Springer, Berlin; 1998.
Censor Y, Elfving T: A multiprojection algorithm using Bregman projections in a product space.Numer. Algorithms 1994, 8:221–239. 10.1007/BF02142692
Byrne C: Iterative oblique projection onto convex subsets and the split feasibilityproblem.Inverse Probl. 2002, 18:441–453. 10.1088/0266-5611/18/2/310
Acknowledgements
We thank Prof. Yiju Wang for his careful reading of the manuscript and thank theanonymous referees and the editor for their constructive comments andsuggestions, which greatly improved this article. This project is supported bythe Natural Science Foundation of China (Grant Nos. 11401438, 11171180,11171193, 11126233), and Project of Shandong Province Higher Educational Scienceand Technology Program (Grant No. J14LI52).
Author information
Authors and Affiliations
Corresponding authors
Additional information
Competing interests
The authors declare that there is no conflict of interests regarding the publicationof this paper.
Authors’ contributions
The authors have contributed in this work on an equal basis. All authors read andapproved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Che, H., Li, M. A simultaneous iterative method for split equality problems of two finitefamilies of strictly pseudononspreading mappings without prior knowledge ofoperator norms. Fixed Point Theory Appl 2015, 1 (2015). https://doi.org/10.1186/1687-1812-2015-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2015-1
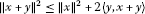 .
.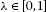 ,
, 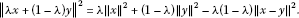
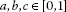 with
with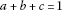 ,
,