- Research
- Open access
- Published:
Vector-valued metrics, fixed points and coupled fixed points for nonlinear operators
Fixed Point Theory and Applications volume 2013, Article number: 218 (2013)
Abstract
In this paper, we will present fixed point theorems for singlevalued and multivalued operators in spaces endowed with vector-valued metrics, as well as a Gnana Bhaskar-Lakshmikantham-type theorem for the coupled fixed point problem, associated to a pair of singlevalued operators (satisfying a generalized mixed monotone property) in ordered metric spaces. The approach is based on Perov-type fixed point theorems in spaces endowed with vector-valued metrics. The Ulam-Hyers stability and the limit shadowing property of the fixed point problems are also discussed.
MSC:47H10, 54H25.
1 Introduction
The classical Banach contraction principle is a very useful tool in nonlinear analysis with many applications to operatorial equations, fractal theory, optimization theory and other topics. Banach contraction principle was extended for singlevalued contraction on spaces endowed with vector-valued metrics by Perov [1] and Perov and Kibenko [2]. For some other contributions to this topic, we also refer to [3–9], etc. The case of multivalued contractions on spaces endowed with vector-valued metrics is treated in [10–12], etc.
In the study of the fixed points for an operator, it is sometimes useful to consider a more general concept, namely coupled fixed points. The concept of coupled fixed point for nonlinear operators was introduced and studied by Opoitsev (see [13–15]) and then, in 1987, by Guo and Lakshmikantham (see [16]) in connection with coupled quasisolutions of an initial value problem for ordinary differential equations. Later, a new research direction for the theory of coupled fixed points in ordered metric spaces was initiated by Gnana Bhaskar and Lakshmikantham in [17] and by Lakshmikantham and Ćirić in [18]. Their approach is based on some contractive type conditions on the operator. For other results on coupled fixed point theory, see [17–22], etc.
Let us recall first some important preliminary concepts and results.
Let X be a nonempty set. A mapping is called a vector-valued metric on X if the following properties are satisfied:
-
(a)
for all ; if , then (where
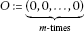 );
); -
(b)
for all ;
-
(c)
for all .
A nonempty set X endowed with a vector-valued metric d is called a generalized metric space in the sense of Perov (in short, a generalized metric space), and it will be denoted by . The notions of convergent sequence, Cauchy sequence, completeness, open and closed subset, open and closed ball, … are similar to those for usual metric spaces.
Notice that the generalized metric space in the sense of Perov is a particular case of Riesz spaces (see [23, 24]) and of so-called cone metric spaces (or K-metric space) (see [25, 26]).
We denote by the set of all matrices with positive elements and by I the identity matrix. If , and , then, by definition
Notice that through this paper, we will make an identification between row and column vectors in .
Definition 1.1 A square matrix of real numbers is said to be convergent to zero if and only if its spectral radius is strictly less than 1. In other words, this means that all the eigenvalues of A are in the open unit disc, i.e., , for every with , where I denotes the unit matrix of (see [27]).
A classical result in matrix analysis is the following theorem (see [27, 28]).
Theorem 1.2 Let . The following assertions are equivalent
-
(i)
A is convergent towards zero;
-
(ii)
as ;
-
(iii)
The matrix is nonsingular and
(1) -
(iv)
The matrix is nonsingular and has nonnegative elements;
-
(v)
and as , for each ;
-
(vi)
The matrices qA and Aq converge to O for each , where .
If X is a nonempty set and is an operator, then
We recall now Perov’s fixed point theorem (see [1], see also [2]).
Theorem 1.3 (Perov)
Let be a complete generalized metric space, and let the operator be with the property that there exists a matrix convergent towards zero such that
Then
-
(1)
;
-
(2)
the sequence of successive approximations , is convergent in X to , for all ;
-
(3)
one has the following estimation
(2) -
(4)
if is an operator such that there exists , and there exists with for each such that
then
-
(5)
if is an operator, , and there exists with for each such that
we have the following estimation
Notice that in Precup [9], as well as in [3, 5] and [7] are pointed out the advantages of working with vector-valued norm with respect to the usual scalar norms.
There is a vast literature concerning this approach, see also, for example, [4, 6, 8, 9, 29], etc.
We will focus our attention to the following system of operatorial equations
where are two given operators.
By definition, a solution of the above system is called a coupled fixed point for the operators and . Notice that if is an operator and we define
then we get the classical concept of a coupled fixed point for the operator S introduced by Opoitsev and then intensively studied in some papers by Guo and Lakshmikantham, Gnana Bhaskar and Lakshmikantham, Lakshmikantham and Ćirić, etc.
The case of an operatorial inclusion is defined in a similar way, namely, by using the symbol ∈ instead of =. The concept of a coupled fixed point for a multivalued operator S is accordingly defined.
First aim of this work is to present some existence and stability results for fixed point equations and inclusions in generalized metric spaces in the sense of Perov. Our second purpose is to present, in the setting of an ordered metric space, a Gnana Bhaskar-Lakshmikantham-type theorem for the coupled fixed point problem associated to a pair of singlevalued operators satisfying a generalized mixed monotone assumption. The approach is based on an abstract fixed point theorem in ordered complete metric spaces. Our results are related with other existence and stability results for the a coupled fixed point problem for singlevalued operators proved in [30] by the support of Perov’s fixed point theorem.
2 Existence, uniqueness and stability for fixed point equations and inclusions
We start this section by an extension of Perov’s theorem. At the same time, the result is a generalization to vector-valued metric spaces of the main theorem in [31].
Theorem 2.1 Let be a generalized complete metric space, and let be an almost contraction with matrices A, B and C, i.e., the matrix converges to zero, and
Then, the following conclusions hold
-
1.
f has at least one fixed point in X and, for each , the sequence of successive approximations of f starting from converges to as ;
-
2.
For each , we have
and
-
3.
If, additionally, the matrix converges to zero, then f has a unique fixed point in X.
Proof Let be arbitrary, and consider the sequence of successive approximations for f starting from , i.e.,
We have that .
Inductively, we get that the sequence satisfies, for all , the following estimation
Hence, for all and , , we get that
Thus, , as . Hence is a Cauchy sequence in the complete metric space . Thus, converges to a certain element .
Next, we show that . Indeed, we have the following estimation
Hence . In addition, letting in the estimation of , we get
For , we obtain
We show now the uniqueness of the fixed point.
Let with . Then
Thus . Since converges to zero, we get that is non-singular and . Hence and so . □
Remark 2.2 The result above extends Corollary 2.3 in [5], where the case of almost contractions with matric is treated.
Two important abstract concepts are given now.
If is a generalized metric space, then is called a weakly Picard operator if and only if the sequence of successive approximations of f converges for all and the limit (which may depend on x) is a fixed point of f.
If f is weakly Picard operator, then we define the operator by
Notice that, in this case, . Moreover, is a set retraction of X to .
If f is weakly Picard operator and , then by definition f is a Picard operator. In this case, is the constant operator, i.e., for all .
Definition 2.4 (see [33])
Let be a generalized metric space, and let be an operator. Then, f is said to be a ψ-weakly Picard operator if and only if f is a weakly Picard operator and is an increasing operator, continuous in O with such that
Moreover, a ψ-weakly Picard operator with a unique fixed point is said to be a ψ-Picard operator. In particular, if is given by (with ), then we say that f is M-weakly Picard operator (respectively a M-Picard operator).
From Theorem 2.1, we get the following example.
Example 2.5 If is a generalized complete metric space and is an almost contraction with matrices A, B, and C, then f is a ψ-weakly Picard operator with the function . In particular, if is a contraction with matrix A, then f is a ψ-Picard operator with .
For the proof of our next theorems we need the following notion.
Definition 2.6 Let be a generalized metric space, and let be an operator. Then, the fixed point equation
is said to be generalized Ulam-Hyers stable if there exists an increasing function , continuous in O with such that for any with for and any ε-solution of (4), i.e.,
there exists a solution of (4) such that
In particular, if , (where ), then the fixed point equation (4) is called Ulam-Hyers stable.
We can prove now the following abstract result (see also Rus [33]) concerning the Ulam-Hyers stability of the fixed point equation (4).
Theorem 2.7 Let be a generalized metric space, and let be a ψ-weakly Picard operator. Then, the fixed point equation (4) is generalized Ulam-Hyers stable.
Proof Let (with for ), and let be a ε-solution of (5), i.e., . Since f is a ψ-Picard operator, we have that
Hence, there exists such that
□
Remark 2.8 In particular, if is a generalized complete metric space, and is an almost contraction with matrices A, B and C, then, by Example 2.5 and Theorem 2.7, we get that the fixed point equation (4) is Ulam-Hyers stable.
We now move our attention to the multivalued case. If is a metric space, and we denote by the space of all nonempty subsets of X, then the gap functional (generated by ρ) on is defined as
In particular, if , we put in place of .
We will denote by the Pompeiu-Hausdorff functional on , defined as
Let be a generalized metric space with .
Notice that d is a generalized metric on X if and only if are metrics on X for each .
We denote by
and by
It is well known that if is a metric on X, and , then if and only if , where denotes the closure of Y in . As a consequence,
Hence, for each is equivalent with for each , which is also equivalent with .
Since , we have:
-
(a)
for each .
-
(b)
Y is closed with respect to is closed with respect to each for .
We denote by the set of all nonempty closed (with respect to d) subsets of X.
We have the following two auxiliary results.
Lemma 2.9 Let be a generalized metric space, let , and let . Then,
Lemma 2.10 Let be a generalized metric space, , . Then, for any , there exists such that
If is a nonempty set, and is a multivalued operator, then the graph of the operator F is denoted by
while the fixed point set and, respectively, the strict fixed point set of F are denoted by the symbols
We will present now an extension of the Nadler fixed point theorem in a space endowed with a vector-valued metric, which is also a multivalued version of Perov’s theorem.
Theorem 2.11 Let be a generalized complete metric space, and let be a multivalued almost contraction with matrices A and B, i.e., there exists two matrices such that A converges to zero and
Then
-
(i)
;
-
(ii)
for each , there exists a sequence (with , and for each ) such that is convergent to a fixed point of F, and the following relations hold
and
Proof Let and be arbitrarily chosen. Let , where Q is defined by Theorem 1.2. Then, by Lemma 2.10, there exists such that
Inductively, there exists such that
We have
Thus
Letting , we get that is a Cauchy sequence in X. Since is complete, it follows that there exists such that , . Thus,
Letting , we get that . By Lemma 2.9, we get that . Moreover, letting in (7), we obtain
Thus,
Letting , we get that . □
For the following notions see Rus et al. [34] and A. Petruşel [10].
Definition 2.12 Let be a generalized metric space, and let be a multivalued operator. By definition, F is a multivalued weakly Picard (briefly MWP) operator if for each , there exists a sequence such that
-
(i)
, ;
-
(ii)
, for each ;
-
(iii)
the sequence is convergent, and its limit is a fixed point of F.
Remark 2.13 A sequence satisfying the condition (i) and (ii) in the definition above is called a sequence of successive approximations of F starting from .
If is an MWP operator, then we define by the formula := {| there exists a sequence of successive approximations of F starting from that converges to z}.
Definition 2.14 Let be a generalized metric space, and let be an MWP operator. Then, F is called a ψ-multivalued weakly Picard operator (briefly ψ-MWP operator) if and only if is an increasing operator, continuous in O with , and there exists a selection of such that
Example 2.15 Let be a generalized complete metric space, and let be a multivalued almost contraction with matrices A and B. Then, by Theorem 2.11 (see (i) and (ii)), we get that F is a -MWP operator.
Two important stability concepts are given now.
Definition 2.16 Let be a generalized metric space, and let be a multivalued operator. The fixed point inclusion
is called generalized Ulam-Hyers stable if and only if there exists increasing, continuous in O with such that for each (with for ) and for each ε-solution of (8), i.e.,
there exists a solution of the fixed point inclusion (8) such that
In particular, if for each (where ), then the fixed point inclusion (8) is said to be Ulam-Hyers stable.
Definition 2.17 Let be a generalized metric space, and let be a multivalued operator. Then, the multivalued operator F is said to have the limit shadowing property if for each sequence in X such that as , there exists a sequence of successive approximations of F such that as .
An auxiliary result is as follows.
Cauchy-type lemma Let be a matrix convergent toward zero and be a sequence such that . Then
We can prove now the Ulam-Hyers stability of the fixed point inclusion (8) for the case of a multivalued contraction, which has at least one strict fixed point. The limit shadowing property is also established.
Theorem 2.18 Let be a generalized complete metric space, and let be a multivalued A-contraction, i.e., there exists a matrix such that A converges to zero and
Suppose also that , i.e., there exists such that . Then
-
(a)
the fixed point inclusion (8) is Ulam-Hyers stable;
-
(b)
the multivalued operator F has the limit shadowing property.
Proof (a) Let (with for ), and let be an ε-solution of (8), i.e., . Let be such that . Then
Thus .
(b) Let be a sequence in X such that as . We shall prove first that as . We successively have
By Cauchy’s lemma, the right hand side tends to O as . Thus as .
On the other hand, by Theorem 2.11(i)-(ii), we know that there exists a sequence of successive approximations for F starting from arbitrary , which converge to a fixed point of the operator F. Since, the fixed point is unique, we get that as . Hence, for such a sequence , we have
□
We also have the following abstract results concerning the Ulam-Hyers stability of the fixed point inclusion (8) for multivalued operators.
Theorem 2.19 Let be a generalized metric space, and let be a multivalued ψ-weakly Picard operator. Suppose also that there exists a matrix such that for any (with for ) and any with there exists such that . Then, the fixed point inclusion (8) is generalized Ulam-Hyers stable.
Proof Let (with for ) and be a ε-solution of (8), i.e., . Since F is a multivalued ψ-weakly Picard operator, for each , we have
Now, by our additional assumption, for there exists such that . Thus, define , and we get
□
As an exemplification of the previous theorem, we have the following result.
Let us recall first an important notion. A subset U of a (generalized) metric space is called proximinal if for each there exists such that .
As a consequence of Theorem 2.11 and of the abstract result above, we obtain the following theorem.
Corollary 2.20 Let be a generalized complete metric space, and let be a multivalued A-contraction with proximinal values. Then the fixed point inclusion (8) is Ulam-Hyers stable.
Proof Let (with for ), and let be a ε-solution of (8), i.e., . Since F is an -MWP operator, for each , we have
Since is a proximinal set, there exists such that . Thus, if we consider , we get
□
Remark 2.21 It is an open question to give other examples of how Theorem 2.19 can be applied. A more general open question is to give similar results for multivalued almost contractions with matrices A and B.
For other examples and results regarding the Ulam-Hyers stability and the limit shadowing property of the operatorial equations and inclusions, see Bota-Petruşel [35], Petru-Petruşel-Yao [36], Petruşel-Rus [29] and Rus [32, 33].
3 An application to coupled fixed point results for singlevalued operators without mixed monotone property
Let X be a nonempty set endowed with a partial order relation denoted by ≤. Then we denote
If is an operator, then we denote the Cartesian product of f with itself as follows
Definition 3.1 Let X be a nonempty set. Then is called an ordered generalized metric space if
-
(i)
is a generalized metric space in the sense of Perov;
-
(ii)
is a partially ordered set.
The following result will be an important tool in our approach.
Theorem 3.2 Let be an ordered generalized metric space, and let be an operator. We suppose that
-
(1)
for each there exists such that ;
-
(2)
;
-
(3)
is continuous;
-
(4)
the metric d is complete;
-
(5)
there exists such that ;
-
(6)
there exists a matrix , which converges to zero such that
Then is a Picard operator.
Proof Let be arbitrary. Since , by (6) and (4), we get that there exists such that as . By (3), we get that .
If , then by (2), we have that for each . Thus, by (6), we get that as .
If , then by (1), it follows that there exists such that . By the fact that , as before, we get that as . This together with the fact that implies that as .
Finally, the uniqueness of the fixed point follows by the contraction condition (6) using again the assumption (1). □
Remark 3.3 The conclusion of the theorem above holds if instead of hypothesis (2) we put
(2′) is monotone increasing
or
(2″) is monotone decreasing.
Of course, it is easy to remark that assertion (2) in Theorem 3.2 is more general. For example, if we consider the ordered metric space , then , satisfies (2) for any .
Remark 3.4 Condition (5) from the theorem above is equivalent with
(5′) f has a lower or an upper fixed point in X.
Remark 3.5 For some similar results, see Theorem 4.2 and Theorem 4.7 in [37].
We will apply the above result for the coupled fixed point problem generated by two operators.
Let X be a nonempty set endowed with a partial order relation denoted by ≤. If we consider , two arbitrary elements of , then, by definition,
Notice that ⪯ is a partial order relation on Z.
We denote
Let be an operator defined by
The Cartesian product of T and T will be denoted by , and it is defined in the following way
The first main result of this section is the following theorem.
Theorem 3.6 Let be an ordered and complete metric space, and let be two operators. We suppose that
-
(i)
for each , which are not comparable with respect to the partial ordering ⪯ on , there exists (which may depend on and ) such that t is comparable (with respect to the partial ordering ⪯) with both z and w, i.e.,
-
(ii)
for all ( and ) or ( and ), we have
-
(iii)
are continuous;
-
(iv)
there exists such that
-
(v)
there exists a matrix convergent toward zero such that
for all ( and ) or ( and ).
Then there exists a unique element such that
and the sequence of the successive approximations converges to as for all .
Proof Denote . We show that Theorem 3.2 is applicable for the operator defined by
Notice first that by (i), we get that if , there exists such that . Thus, the first assumption of Theorem 3.2 holds.
In order to prove (2) from Theorem 3.2, let , be arbitrary elements of (where ( and ) or ( and )) such that
From we get that , that is
By a similar approach, we alternatively have that
Using (11) and (12), we get that
Thus, we get , which implies that
In order to obtain (5) from Theorem 3.2, notice first that since there exists such that
we obtain that
Thus, we have . By a similar approach, we alternatively obtain that . Thus, .
Finally, in order to prove hypotheses (3) and (6) from Theorem 3.2, we define the mapping by
Notice now that if is an ordered metric space, then is an ordered generalized metric space. The completeness of follows from the completeness of d. Notice also that the continuity of T follows by (iii). For hypothesis (6), we successively have
Hence
Thus, the triple and the operator satisfy all the hypothesis of Theorem 3.2. Hence, T is a Picard operator, and so, the equation has a unique solution , and the sequence of successive approximations of the operator T, starting from any converges to . Thus, the unique element satisfies the system
and as , where and
for all , . □
For the particular case of classical coupled fixed point problems (i.e., and , where is a given operator) we get (by Theorem 3.6) the following generalization of the Gnana Bhaskar-Lakshmikantham theorem in [17].
Theorem 3.7 Let be an ordered and complete metric space, and let be an operator. We suppose that
-
(i)
for each , which are not comparable with respect to the partial ordering ⪯ on , there exists (which may depend on and ) such that t is comparable (with respect to the partial ordering ⪯) with both z and w;
-
(ii)
for all ( and ) or ( and ), we have
-
(iii)
is continuous;
-
(iv)
there exists such that
-
(v)
there exist with such that
for all ( and ) or ( and ).
Then there exists a unique element such that
and the sequence of the successive approximations converges to as for all .
As an application of the previous theorem, we get now an existence and uniqueness result for a system of functional-integral equations, which appears in some traffic flow models.
By a solution of the previous system, we understand a couple , which satisfies the system for all .
As before, we consider on the following partial ordering relation
and the supremum norm
Notice that, as before, the partial ordering relation generates on a partial ordering .
If we define
then, the above system can be represented as a coupled fixed point problem
An existence and uniqueness result for the system (18) is the following theorem.
Theorem 3.8 Let and be two continuous mappings. We suppose that
-
(i)
there exists such that
-
(ii)
-
(a)
is increasing for all , and is increasing, is decreasing and is increasing for all ,
or
-
(b)
is decreasing for all , and is decreasing, is increasing and is decreasing for all , ;
-
(a)
-
(iii)
there exist such that
for all and ;
-
(iv)
there exist such that for all and , we have
-
(v)
.
Then, there exists a unique solution of system (18).
Proof From the hypotheses, we get that all the assumptions of Theorem 3.7 are satisfied for the operator
where . □
We introduce now the concept of Ulam-Hyers stability for coupled fixed point problems.
Definition 3.9 Let be a metric space, and let be two operators. Then the operatorial equations system
is said to be Ulam-Hyers stable if there exist such that for each and each pair such that
there exists a solution of (19) such that
It is an open problem to obtain Ulam-Hyers stability results for the coupled fixed point problem in the context of ordered metric spaces. For several results on this subject, see [35, 36].
Remark 3.10 The case of a system of operatorial inclusions of the form
(where are two given multivalued operators) can be treated in a similar way.
References
Perov AI: On the Cauchy problem for a system of ordinary differential equations. Pviblizhen. Met. Reshen, Differ. Uravn. 1964, 2: 115–134.
Perov AI, Kibenko AV: On a certain general method for investigation of boundary value problems. Izv. Akad. Nauk SSSR, Ser. Mat. 1966, 30: 249–264. (in Russian)
Bucur A, Guran L, Petruşel A: Fixed points for multivalued operators on a set endowed with vector-valued metrics and applications. Fixed Point Theory 2009, 10(1):19–34.
Agarwal RP: Contraction and approximate contraction with an application to multi-point boundary value problems. J. Comput. Appl. Math. 1983, 9: 315–325. 10.1016/0377-0427(83)90003-1
Filip AD, Petruşel A: Fixed point theorems on spaces endowed with vector-valued metrics. Fixed Point Theory Appl. 2009., 2010: Article ID 281381
O’Regan D, Shahzad N, Agarwal RP Fixed Point Theory and Applications. In Fixed Point Theory for Generalized Contractive Maps on Spaces with Vector-Valued Metrics. Nova Science Publishers, New York; 2007:143–149.
Precup R, Viorel A: Existence results for systems of nonlinear evolution equations. Int. J. Pure Appl. Math. 2008, 47(2):199–206.
Precup R, Viorel A: Existence results for systems of nonlinear evolution inclusions. Fixed Point Theory 2010, 11(2):337–346.
Precup R: The role of matrices that are convergent to zero in the study of semilinear operator systems. Math. Comput. Model. 2009, 49: 703–708. 10.1016/j.mcm.2008.04.006
Petruşel A: Multivalued weakly Picard operators and applications. Sci. Math. Jpn. 2004, 59: 169–202.
Petre IR, Petruşel A: Krasnoselskii’s theorem in generalized Banach spaces and applications. Electron. J. Qual. Theory Differ. Equ. 2012, 85: 1–20.
Rezapour S, Amiri P: Some fixed point results for multivalued operators in generalized metric spaces. Comput. Math. Appl. 2011, 61: 2661–2666.
Opoitsev VI: Heterogenic and combined-concave operators. Syber. Math. J. 1975, 16: 781–792. (in Russian)
Opoitsev VI: Dynamics of collective behavior. III. Heterogenic systems. Avtom. Telemeh. 1975, 36: 124–138. (in Russian)
Opoitsev VI, Khurodze TA: Nonlinear Operators in Spaces with a Cone. Tbilis. Gos. Univ., Tbilisi; 1984:271. (in Russian)
Guo D, Lakshmikantham V: Coupled fixed points of nonlinear operators with applications. Nonlinear Anal. 1987, 11: 623–632. 10.1016/0362-546X(87)90077-0
Gnana Bhaskar T, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal. 2006, 65: 1379–1393. 10.1016/j.na.2005.10.017
Lakshmikantham V, Ćirić L: Coupled fixed point theorems for nonlinear contractions in partially ordered metric spaces. Nonlinear Anal. 2009, 70: 4341–4349. 10.1016/j.na.2008.09.020
Guo D, Cho YJ, Zhu J: Partial Ordering Methods in Nonlinear Problems. Nova Science Publishers, Hauppauge; 2004.
Hong S: Fixed points for mixed monotone multivalued operators in Banach spaces with applications. J. Math. Anal. Appl. 2008, 337: 333–342. 10.1016/j.jmaa.2007.03.091
Rus, MD: The method of monotone iterations for mixed monotone operators. PhD thesis, Babeş-Bolyai University Cluj-Napocaac (2010)
Berinde V: Generalized coupled fixed point theorems for mixed monotone mappings in partially ordered metric spaces. Nonlinear Anal. 2011, 74: 7347–7355. 10.1016/j.na.2011.07.053
Luxemburg WAJ, Zaanen AC 1. In Riesz Spaces I. North-Holland, Amsterdam; 1971.
Luxemburg WAJ, Zaanen AC: Riesz Spaces II. North-Holland, Amsterdam; 1983.
Zabrejko PP: K -metric and K -normed linear spaces: survey. Collect. Math. 1997, 48(4–6):825–859.
Huang L-G, Zhang X: Cone metric spaces and fixed point theorems of contractive mappings. J. Math. Anal. Appl. 2007, 332: 1468–1476. 10.1016/j.jmaa.2005.03.087
Varga RS Springer Series in Computational Mathematics 27. In Matrix Iterative Analysis. Springer, Berlin; 2000.
Allaire G, Kaber SM: Numerical Linear Algebra. Springer, New York; 2008.
Petruşel A, Rus IA: The theory of a metric fixed point theorem for multivalued operators. In Fixed Point Theory and Its Applications. Edited by: Lin LJ, Petrusel A, Xu HK. Yokohama Publ., Yokohama; 2010:167–176.
Urs C: Coupled fixed point theorems and applications. Miskolc Math. Notes 2013, 14(1):323–333.
Berinde M, Berinde V: On a general class of multi-valued weakly Picard mappings. J. Math. Anal. Appl. 2007, 326: 772–782. 10.1016/j.jmaa.2006.03.016
Rus IA: The theory of a metrical fixed point theorem: theoretical and applicative relevances. Fixed Point Theory 2008, 9(2):541–559.
Rus IA: Remarks on Ulam stability of the operatorial equations. Fixed Point Theory 2009, 10(2):305–320.
Rus IA, Petruşel A, Sîntămărian A: Data dependence of the fixed points set of some multivalued weakly Picard operators. Nonlinear Anal. 2003, 52: 1947–1959. 10.1016/S0362-546X(02)00288-2
Bota M, Petruşel A: Ulam-Hyers stability for operatorial equations. An. Stiint. Univ. Al. I. Cuza Iasi. Mat. (N.S.) 2011, 57: 65–74.
Petru PT, Petruşel A, Yao JC: Ulam-Hyers stability for operatorial equations and inclusions via nonself operators. Taiwan. J. Math. 2011, 15(5):2195–2212.
Petruşel A, Rus IA: Fixed point theorems in ordered L -spaces. Proc. Am. Math. Soc. 2005, 134(2):411–418. 10.1090/S0002-9939-05-07982-7
Acknowledgements
(1) For the first author, this paper was supported by a grant of the Romanian National Authority for Scientific Research, CNCS-UEFISCDI, project number PN-II-ID-PCE-2011-3-0094, while for the third author, this work was possible with the financial support of the Sectoral Operational Programme for Human Resources Development 2007-2013, co-financed by the European Social Fund, under the project number POSDRU/107/1.5/S/76841 with the title Modern Doctoral Studies: Internationalization and Interdisciplinarity. (2) The authors are thankful to the reviewers for the careful reading of the paper and fruitful comments which improved the quality of the paper in a significant way.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The authors declare that the first two authors on one hand and the third author on the other hand have equal contributions to this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Petruşel, A., Petruşel, G. & Urs, C. Vector-valued metrics, fixed points and coupled fixed points for nonlinear operators. Fixed Point Theory Appl 2013, 218 (2013). https://doi.org/10.1186/1687-1812-2013-218
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2013-218
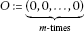 );
);