KKM lemmas and minimax inequality theorems in abstract convexity spaces

Abstract

The purpose of this paper is to give some further results in a type of generalized convexity spaces. First, we prove that an abstract convex space has KKM property if and only if it has a strong Fan-Browder property. Then we introduce an abstract convex structure via an upper semi-continuous multi-valued mapping and establish some generalized versions of KKM lemma. By employing our general KKM lemmas, we derive some generalizations of minimax inequalities, which contain several existing ones as special cases.

1 Introduction

Many problems in nonlinear analysis can be solved by nonempty intersection of a certain family of subsets of an underlying set. One of the remarkable results on such nonempty intersection is the celebrated Knaster-Kuratowski-Mazurkiewicz theorem (simply, KKM lemma) in 1929 [1], which is concerned with certain types of multi-valued mappings later called the KKM maps. Ky Fan [2] extends this method to Fan-KKM lemma and Fan’s minimax inequality, which have played very important roles in the study of modern nonlinear analysis. At the beginning, KKM theory named by Park [3] was mainly concerned with original convex subsets of topological vector spaces. Later, it has been extended to convex spaces by Lassonde [4], and to spaces having certain families of contractible subsets (simply, C-spaces or H-spaces) by Horvath [5–7]. Moreover, a great deal of effort has gone into KKM theory and its applications such as generalized convexity (simply,G-spaces) and others (see, Park [8–11]).

In KKM theory, the convexity of space plays a very important role. There are many works, dealing with various kinds of generalized, topological, or axiomatically-defined convexities (see, [4–19]). Most of them are to establish various KKM lemmas, fixed point theorems and selection theorems in topological spaces without linear structure. The question is whether the various convexity structures should have some common characteristic. Regarding these questions, the authors of [20] prove that in a sense, $H_0$-condition is necessary for a convexity structure to ensure the existence of fixed points or continuous selections of mappings.

The purpose of this paper is to give some further results in generalized convexity spaces. We prove that an abstract convex space has a KKM property if and only if it has a strong Fan-Browder property. Then we introduce an abstract convexity structure via an upper semi-continuous multi-valued mapping and establish some generalized versions of KKM lemma. By employing our general KKM lemmas, we derive some generalizations of minimax inequalities, in which the functions φ are defined on the sets of two different linear topological spaces or have a weaker convexity condition.

2 Preliminaries

Throughout the work, we assume that Y is nonempty. Let $2^Y$ denote the class of all subsets of Y, and let $〈Y〉$ denote the class of all nonempty finite subsets of Y.

As the basic framework of this paper, let us start with an abstract convexity structure, of which many generalized convexity structures are some special cases (see, [18, 21]).

Definition 2.1 A pair $(Y,\math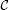cal{C})$, where is a family of subsets of Y, called a convex structure if

• (1) ∅ and Y belong to ;

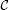• (2) 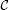is closed for arbitrary intersection: ${\bigcap }_{A\in \mathcal{D}}A\in \mathcal{C}$ for each family of subsets $\mathcal{D}\subset \mathcal{C}$.

Then the pair $(Y,\mathcal{C})$ is called an abstract convexity space. Let $(Y,\mathcal{C})$ be an abstract convexity space. The convex hull ${co}_{\mathcal{C}}$ is defined as

$${co}_{\mathcal{C}}(A)=\bigcap \{D\in \mathcal{C}:A\subset D\},\mathrm{\forall }A\subset Y.$$

A subset C of Y is said to be a convex subset if $C\in \mathcal{C}$. It is clear that C is convex if and only if ${co}_{\mathcal{C}}(C)=C$, and it is easy to check that this convexity structure includes various abstract convexity structures mentioned above (see, [20]). For example, in Horvath’s H-spaces, the class of a ‘convex’ set

$$\mathcal{C}=\{C\subset Y:{\mathrm{\Gamma }}_A\subset C\text{ for any finite subset }A\subset C\},$$

where $\{{\mathrm{\Gamma }}_A\}$ is a family of contractible subsets of Y indexed by all finite subsets of Y such that ${\mathrm{\Gamma }}_A\subset {\mathrm{\Gamma }}_B$, whenever $A\subset B$ (see, [5–7]).

Let $(Y,\mathcal{C})$ be an abstract convexity space, let X be a subset of Y, and let $F:X\mapsto 2^Y$ be a multi-valued mapping. F is said to be convex-valued if for each $x\in X$, $F(x)$ is convex (i.e., for each $x\in X$ and any finite subset $\{y_0,y_1,\dots ,y_n\}\subset F(x)$, ${co}_{\mathcal{C}}\{y_0,y_1,\dots ,y_n\}\subset F(x)$). Let Y be a topological space. F is said to be nonempty-valued (respectively, compact-valued) if for each $x\in X$, $F(x)$ is nonempty (respectively, compact).

Definition 2.2 Let $(Y,\mathcal{C})$ be an abstract convexity space, let X be a subset of Y, and let $F:X\mapsto 2^X$ be a multi-valued mapping. F is said to be weakly convex-valued if for each $x\in X$ and any finite subset $\{y_0,y_1,\dots ,y_n\}\subset F(x)$, ${co}_{\mathcal{C}}\{y_0,y_1,\dots ,y_n\}\subset F(x)$, whenever $x\in {co}_{\mathcal{C}}\{y_0,y_1,\dots ,y_n\}$.

Remark 2.3 It is clear that F is convex-valued, then F is weakly convex-valued.

Let $(Y,\mathcal{C})$ be an abstract convexity space and X be a subset of Y.

• (i) $F:X\mapsto 2^Y$ is said to be a KKM mapping if for each $A\in 〈X〉$, F satisfies

  $${co}_{\mathcal{C}}(A)\subset \bigcup _{x\in A}F(x).$$

• (ii) $F:X\mapsto 2^X$ is said to be a Fan-Browder mapping if F is convex-valued and has relatively open preimages in X (i.e., $F(x)$ is convex for each $x\in X$ and $F^{-1}(y)$ is open in X for each $y\in X$).

• (iii) $F:X\mapsto 2^X$ is said to be a weak Fan-Browder mapping if F is weakly convex- valued and has relatively open preimages in X.

Let $(Y,\mathcal{C})$ be an abstract convexity space, and let X be a subset of Y. X is said to be of KKM property (briefly KKMP) if every KKM mapping $F:X\mapsto 2^Y$ with close values has a finite intersection property (i.e., ${\bigcap }_{x\in A}F(x)\ne \mathrm{\varnothing }$ for each $A\in 〈X〉$). X is said to be of Fan-Browder fixed point property (briefly FBFP) if every Fan-Browder mapping $F:X\mapsto 2^X$ with nonempty values has a fixed point. X is said to be of a strong Fan-Browder fixed point property (briefly SFBFP) if every weak Fan-Browder mapping $F:X\mapsto 2^X$ with nonempty values has a fixed point.

The following is just an inverse negative proposition of SFBFP.

Proposition 2.4 Let $(Y,\mathcal{C})$ be an abstract convexity space, and let X be a subset of Y. Then X has SFBFP if and only if, for every weak Fan-Browder mapping $F:X\mapsto 2^X$, there exists some $\hat{x}\in X$ such that $F(\hat{x})=\mathrm{\varnothing }$, whenever F has no fixed point.

3 KKM property and Fan-Browder fixed point property

In this section, we give an equivalent relation between KKMP and SFBFP.

Theorem 3.1 Let $(Y,\mathcal{C})$ be an abstract convexity space, and let X be a compact subset of $(Y,\mathcal{C})$. Then X has KKMP if and only if it has SFBFP.

Proof For any mapping $F:X\mapsto 2^Y$, denote $T:X\mapsto 2^X$ by

$$T(x)=X\setminus F^{-1}(x),\mathrm{\forall }x\in X.$$

Before proving the equivalence between KKMP and SFBFP, the following contrapositives are needed:

• (i) $\{x:T(x)=\mathrm{\varnothing }\}={\bigcap }_{x\in X}F(x)$ and $\{x:F(x)=\mathrm{\varnothing }\}={\bigcap }_{x\in X}T(x)$.

• (ii) If $F:X\mapsto 2^Y$ is a KKM mapping with closed values, then $T:X\mapsto 2^X$ is a weak Fan-Browder mapping with no fixed point.

• (iii) If $F:X\mapsto 2^X$ is a weak Fan-Browder mapping with no fixed point, then $T:X\mapsto 2^X$ is a KKM mapping with closed values.

We first prove (i), (ii) and (iii).

• (1) It is easy to check that (i) holds.

• (2) Let $F:X\mapsto 2^Y$ be a KKM mapping with closed values. If $x\in X$, then

  $$T^{-1}(x)=\{y\in X:x\in T(y)\}=\{y\in X:x\in X\setminus F^{-1}(y)\}=X\setminus F(x)$$

is an open subset in X. On the other hand, if T has a fixed point, suppose $x^{\ast }\in X$ and $x^{\ast }\in T(x^{\ast })$. Then $x^{\ast }\in X\setminus F^{-1}(x^{\ast })$, so $x^{\ast }\notin F(x^{\ast })$, which contradicts that F is a KKM mapping. Hence T has no fixed point. It remains to show that T is weakly convex-valued. Fix $x\in X$, and let $\{y_0,y_1,\dots ,y_m\}\subset T(x)$ be an arbitrary finite subset. By Definition 2.2, it suffices to show that $x\notin {co}_{\mathcal{C}}\{y_0,y_1,\dots ,y_n\}$. Indeed, since $\{y_0,y_1,\dots ,y_m\}\subset T(x)$, $y_j\in T(x)=X\setminus F^{-1}(x)$ for each $j=0,1,\dots ,m$, so $x\notin {\bigcup }_{j=0}^{m}F(y_j)$. Note that F is a KKM mapping. Then ${co}_{\mathcal{C}}\{y_0,y_1,\dots ,y_m\}\subset {\bigcup }_{j=0}^{m}F(y_j)$, which implies $x\notin {co}_{\mathcal{C}}\{y_0,y_1,\dots ,y_n\}$. Hence T is a weak Fan-Browder mapping, and (ii) is proved.

(3) Let $F:X\mapsto 2^X$ be a weak Fan-Browder mapping with no fixed point. Since F has relatively open preimages, $T(x)=X\setminus F^{-1}(x)$ is closed for each $x\in X$. Let $\{x_0,x_1,\dots ,x_n\}\subset X$ be an arbitrary finite subset. It remains to show that ${co}_{\mathcal{C}}\{x_0,x_1,\dots ,x_n\}\subset {\bigcup }_{i=0}^{n}T(x_i)$. If not, there exists some $x^{\ast }\in {co}_{\mathcal{C}}\{x_0,x_1,\dots ,x_n\}$ such that $x^{\ast }\notin {\bigcup }_{i=0}^{n}T(x_i)$. It follows that $x^{\ast }\in {\bigcap }_{i=0}^n{F}^{-1}(x_i)$, which implies that $x_i\in F(x^{\ast })$ for each $i=0,1,\dots ,n$, that is, $\{x_0,x_1,\dots ,x_n\}\subset F(x^{\ast })$. Note that F is weakly convex-valued and $x^{\ast }\in {co}_{\mathcal{C}}\{x_0,x_1,\dots ,x_n\}$. Then $x^{\ast }\in {co}_{\mathcal{C}}\{x_0,x_1,\dots ,x_n\}\subset F(x^{\ast })$, which contradicts that F has no fixed point. Hence T is a KKM mapping with closed values, and (iii) is proved.

Next we prove that KKMP is equivalent to SFBFP.

KKMP ⇒ SFBFP: Let $F:X\mapsto 2^X$ be a weak Fan-Browder mapping with no fixed point. By Proposition 2.4, what follows to show is that there exists some $\hat{x}\in X$ such that $F(\hat{x})=\mathrm{\varnothing }$. By (ii), T is a KKM mapping with closed values. Then $\{T(x):x\in X\}$ has a finite intersection property and hence ${\bigcap }_{x\in X}T(x)\ne \mathrm{\varnothing }$ by the compactness of X. Thus there exists some $\hat{x}\in X$ such that $\hat{x}\in {\bigcap }_{x\in X}T(x)=\{x:F(x)=\mathrm{\varnothing }\}\ne \mathrm{\varnothing }$. This implies that $F(\hat{x})=\mathrm{\varnothing }$.

SFBFP ⇒ KKMP: Let $F:X\mapsto 2^Y$ be a KKM mapping with closed values. By (ii), T is a weak Fan-Browder mapping with no fixed point. Since X has SFBFP, there exists some $\hat{x}\in X$ such that $T(\hat{x})=\mathrm{\varnothing }$, and (i) implies $\hat{x}\in \{x:T(x)=\mathrm{\varnothing }\}={\bigcap }_{x\in X}F(x)\ne \mathrm{\varnothing }$. In particular, X has a finite intersection property. □

Corollary 3.2 Let $(Y,{co}_{\mathcal{C}})$ be an abstract convexity space, and let X be a compact subset of $(Y,{co}_{\mathcal{C}})$. If X has KKMP, then it has FBFP.

4 An abstract convexity structure

In this section, we introduce an abstract convexity structure via an upper semi-continuous multi-valued mapping and establish some generalized versions of KKM lemma based on this convexity structure.

Let $N=\{0,1,2,\dots ,n\}$, ${\mathrm{\Delta }}_n=e^0{e}^1\cdots e^n$ be the standard simplex of dimension n, where $\{e^0,e^1,\dots ,e^n\}$ is the canonical basis of $R^{n+1}$, and for $J\subset N$, let ${\mathrm{\Delta }}_J=co\{e^j:j\in J\}$ be a face of ${\mathrm{\Delta }}_n$.

Definition 4.1 Let Y be a compact set of a topological space, let ${\mathrm{\Delta }}_n=e^0{e}^1\cdots e^n$ be the standard simplex, and let $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ be a multi-valued mapping. If for each continuous mapping $p:Y\mapsto {\mathrm{\Delta }}_n$ (called a simplex mapping), there exists some $x_0\in {\mathrm{\Delta }}_n$ such that $x_0\in p\cdot q(x_0)$, then we say that q has a fixed point property with respect to ${\mathrm{\Delta }}_n$ and simplex mappings.

Lemma 4.2 Let Y be a metric space, let $\{F_0,F_1,\dots ,F_n\}$ be a family of closed subsets of Y. If there exists an upper semi-continuous mapping $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ such that

$$q({\mathrm{\Delta }}_J)\subset \bigcup _{j\in J}{F}_i,\mathrm{\forall }J\subset N=\{0,1,\dots ,n\},$$

and q has a fixed point property with respect to ${\mathrm{\Delta }}_n$ and simplex mappings. Then ${\bigcap }_{i=0}^n{F}_i\ne \mathrm{\varnothing }$.

Proof Suppose that ${\bigcap }_{i=0}^n{F}_i=\mathrm{\varnothing }$. Denote ${\beta }_i:Y\mapsto [0,1]$ by

$${\beta }_i(y)=\frac{d(y,F_i)}{{\sum }_{i=0}^{n}d(y,F_i)},i=0,1,\dots ,n;\mathrm{\forall }y\in Y.$$

Then for each $y\in Y$, ${\beta }_i(y)\ge 0$ and ${\sum }_{i=0}^n{\beta }_i(y)=1$.

Define the simplex mapping $p:Y\mapsto {\mathrm{\Delta }}_n$ as follows

$$p(y)=\sum _{i=0}^n{\beta }_i(y)e^i,\mathrm{\forall }y\in Y.$$

Let $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ be an upper semi-continuous mapping such that

$$q({\mathrm{\Delta }}_J)\subset \bigcup _{j\in J}{F}_i,\mathrm{\forall }J\subset N=\{0,1,\dots ,n\},$$

and q has fixed point property with respect to ${\mathrm{\Delta }}_n$ and simplex mappings. Then $p\cdot q:{\mathrm{\Delta }}_n\mapsto {\mathrm{\Delta }}_n$ has a fixed point in ${\mathrm{\Delta }}_n$. Let $e\in {\mathrm{\Delta }}_n$, and let $e\in p\cdot q(e)$. Then there exists some $y^{\ast }\in q(e)$ such that $e=p(y^{\ast })={\sum }_{i=0}^n{\beta }_i(y^{\ast })e^i$.

Let $I(y^{\ast })=\{i:{\beta }_i(y^{\ast })>0,i=0,1,\dots ,n\}$. Given $i\in I(y^{\ast })$, we have ${\beta }_i(y^{\ast })>0$ and $y^{\ast }\notin F_i$, and hence $y^{\ast }\notin {\bigcup }_{i\in I(y^{\ast })}{F}_i$.

On the other hand,

$$q(e)=q(p(y^{\ast }))=q(\sum _{i=0}^n{\beta }_i(y^{\ast })e^i)=q(\sum _{i\in I(y^{\ast })}{\beta }_i(y^{\ast })e^i)\subset {co}_{\mathcal{C}}\{y_i:i\in I(y^{\ast })\}.$$

Consequently,

$$y^{\ast }\in q(e)\subset {co}_{\mathcal{C}}\{y_i:i\in I(y^{\ast })\}\subset \bigcup _{i\in I(y^{\ast })}{F}_i,$$

which is a contradiction. □

We obtain the following approximation result, because the partition of unity $\{{\beta }_i\}$, subordinate to the finite covering $\{F_i^c:i=0,1,\dots ,n\}$ of Y, can be given by using the compactness of X instead of the hypothesis of metric space in the proof of Lemma 4.2.

Lemma 4.3 Let Y be a compact space, let $\{F_0,F_1,\dots ,F_n\}$ be a family of closed subsets of Y. If there exists an upper semi-continuous mapping $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ such that

$$q({\mathrm{\Delta }}_J)\subset {co}_{\mathcal{C}}\{y_j:j\in J\},\mathrm{\forall }J\subset N=\{0,1,\dots ,n\},$$

and q has a fixed point property with respect to ${\mathrm{\Delta }}_n$ and simplex mappings. Then ${\bigcap }_{i=0}^n{F}_i\ne \mathrm{\varnothing }$.

Definition 4.4 Let $(Y,\mathcal{C})$ be an abstract convexity space. If for each finite subset $\{y_0,y_1,\dots ,y_n\}\subset Y$ and the standard simplex ${\mathrm{\Delta }}_n=e^0{e}^1\cdots e^n$, there exists multi-valued mapping $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ such that

$$q({\mathrm{\Delta }}_J)\subset {co}_{\mathcal{C}}\{y_j:j\in J\},\mathrm{\forall }J\subset N=\{0,1,\dots ,n\}$$

and q has a fixed point property with respect to ${\mathrm{\Delta }}_n$ and simplex mappings. Then $(Y,\mathcal{C})$ is said to be of $H^q$-property.

Theorem 4.5 Let $(Y,\mathcal{C})$ be an abstract convexity space, $X\subset Y$ be a subset of Y, and $F:X\mapsto 2^Y$ be a KKM mapping with closed values. If Y is a compact topological space or a metric space, and $(Y,\mathcal{C})$ is of $H^q$-property, then $\{F(y):y\in X\}$ has a finite intersection property.

Proof Given an finite subset $\{y_0,y_1,\dots ,y_n\}\subset X$, we prove that ${\bigcap }_{i=0}^{n}F(y_i)\ne \mathrm{\varnothing }$. Since F is a KKM mapping, we have

$${co}_{\mathcal{C}}\{y_j:j\in J\}\subset \bigcup _{i\in J}F(y_j),\mathrm{\forall }J\subset N=\{0,1,\dots ,n\}.$$

Note that $(Y,\mathcal{C})$ is of $H^q$-property. There exists a multi-valued mapping $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ such that

$$q({\mathrm{\Delta }}_J)\subset {co}_{\mathcal{C}}\{y_j:j\in J\},\mathrm{\forall }J\subset N=\{0,1,\dots ,n\},$$

and q has a fixed point property with respect to ${\mathrm{\Delta }}_n$ and simplex mappings.

Consequently,

$$q({\mathrm{\Delta }}_J)\subset \bigcup _{j\in J}F(y_j),\mathrm{\forall }J\subset N=\{0,1,\dots ,n\}.$$

From Lemma 4.2 and 4.3, it follows that ${\bigcap }_{i=0}^{n}F(y_i)\ne \mathrm{\varnothing }$ by using $\{F(y_0),F(y_i),\dots ,F(y_n)\}$ instead of $\{F_0,F_1,\dots ,F_n\}$. □

The latter result follows from Theorem 3.1 and Theorem 4.5.

Corollary 4.6 Let $(Y,\mathcal{C})$ be an abstract convexity space, let $X\subset Y$ be a subset of Y, and let $F:X\mapsto 2^Y$ be a KKM mapping with closed values. If Y is a compact topological space and $(Y,\mathcal{C})$ is of $H^q$-property, then X has a strong Fan-Browder fixed point property.

Let $\{y_0,y_1,\dots ,y_n\}$ be a finite subset of $(Y,{co}_{\mathcal{C}})$. Sometimes it is convenient to construct an upper semi-continuous multi-valued mapping $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ such that

$$q({\mathrm{\Delta }}_J)\subset {co}_{\mathcal{C}}\{y_j:j\in J\},\mathrm{\forall }J\subset N=\{0,1,\dots ,n\}.$$

To see this, we give the following example.

Example 4.7 Let $(Y,\mathcal{C})$ be an abstract convexity space, let $\{y_0,y_1,\dots ,y_n\}$ be a finite subset of $(Y,\mathcal{C})$, and let ${\mathrm{\Delta }}_n=e^0{e}^1\cdots e^n$ be the standard simplex.

Let $I(e)=\{i:e={\sum }_{i=0}^n{t}_i{e}^i,t_i\ge \frac{1}{n}\}$. The multi-valued mapping $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ is defined as

$$q(e)={co}_{\mathcal{C}}\{y_i:i\in I(e)\},\mathrm{\forall }e\in {\mathrm{\Delta }}_n.$$

It is easy to check that $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ is upper semi-continuous and satisfies

$$q({\mathrm{\Delta }}_J)\subset {co}_{\mathcal{C}}\{y_j:j\in J\},\mathrm{\forall }J\subset N=\{0,1,\dots ,n\}.$$

To obtain some results in a specific abstract convexity space, we recall a fixed point theorem (see, [22, 23]).

Lemma 4.8 Let Y be a compact set of a topological space, and let ${\mathrm{\Delta }}_n=e^0{e}^1\cdots e^n$ be the standard simplex. If $p:Y\mapsto {\mathrm{\Delta }}_n$ is continuous, and $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ is an upper semi-continuous mapping with nonempty, closed and contractible values, then there exists some $e\in {\mathrm{\Delta }}_n$ such that $e\in p\cdot q(e)$. Therefore, q has a fixed point property with respect to ${\mathrm{\Delta }}_n$ and simplex mappings.

As an immediate corollary of Lemma 4.2, 4.3 and 4.8, we state the following result.

Corollary 4.9 Let Y be a compact topological space or a metric space, let $\{F_0,F_1,\dots ,F_n\}$ be a family of closed subsets of Y. If there exists an upper semi-continuous mapping $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ with nonempty, closed and contractible values such that

$$q({\mathrm{\Delta }}_J)\subset \bigcup _{i\in J}{F}_i,\mathrm{\forall }J\subset N=\{0,1,\dots ,n\}.$$

Then ${\bigcap }_{i=0}^n{F}_i\ne \mathrm{\varnothing }$.

Definition 4.10 Let $(Y,{co}_{\mathcal{C}})$ be an abstract convexity space. If for each finite subset $\{y_0,y_1,\dots ,y_n\}\subset Y$ and the standard simplex ${\mathrm{\Delta }}_n=e^0{e}^1\cdots e^n$, there exists an upper semi-continuous mapping $q:{\mathrm{\Delta }}_n\mapsto 2^Y$ with nonempty, closed and contractible values such that

$$q({\mathrm{\Delta }}_J)\subset {co}_{\mathcal{C}}\{y_j:j\in J\},\mathrm{\forall }J\subset N=\{0,1,\dots ,n\}.$$

Then $(Y,{co}_{\mathcal{C}})$ is said to be of $H_0^q$-property.

Remark 4.11

• (1) If $(Y,{co}_{\mathcal{C}})$ is of $H_0^q$-property, then $(Y,{co}_{\mathcal{C}})$ is of $H^q$-property.

• (2) Let $(Y,\mathcal{C})$ be an abstract convexity space. If is of $H_0$-property, then it also is of $H_0^q$-property. H-space and G-convexity space have $H_0^q$-property because both of them satisfy $H_0$-condition.

Theorem 4.5 embraces the following special case.

Theorem 4.12 Let $(Y,{co}_{\mathcal{C}})$ be an abstract convexity space, let X be a subset of Y, and let $F:X\mapsto 2^Y$ be a KKM mapping with closed values. If Y is a compact topological space and $(Y,{co}_{\mathcal{C}})$ is of $H_0^q$-property, then $\{F(x):x\in X\}$ has a finite intersection property, and so that X has a strong Fan-Browder fixed point property.

5 Minimax inequalities

As applications, we give some minimax inequality theorems in this section. To prove the main results, we introduce the following lemma.

Lemma 5.1 Let X be a subset of linear topological space, let Y be a compact topological space, and let $s:X\mapsto 2^Y$ be an upper semi-continuous mapping with nonempty, closed and contractible values. Let $F:X\mapsto 2^Y$ be a closed valued mapping such that for each finite subset $\{x_0,x_1,\dots ,x_n\}\subset X$,

$$s(co\{x_0,x_1,\dots ,x_n\})\subset \bigcup _{i=0}^{n}F(x_i).$$

Then ${\bigcap }_{x\in X}F(x)\ne \mathrm{\varnothing }$.

Proof Given a finite subset $\{x_0,x_1,\dots ,x_n\}\subset X$, $p:{\mathrm{\Delta }}_n\mapsto X$ is defined as

$$p(e)=\sum _{i=0}^n{t}_i{x}_i,\mathrm{\forall }e=\sum _{i=0}^n{t}_i{e}^i\in {\mathrm{\Delta }}_n.$$

Let $q=s\cdot p$. Then $q:{\mathrm{\Delta }}_n\mapsto Y$ and satisfies

$$q({\mathrm{\Delta }}_J)=s(p({\mathrm{\Delta }}_J))=s(co\{x_j:j\in J\})\subset \bigcup _{j\in J}F(x_i),\mathrm{\forall }J\subset N=\{0,1,\dots ,n\}.$$

By Corollary 4.9, ${\bigcap }_{i=0}^{n}F(x_i)\ne \mathrm{\varnothing }$. Since Y is compact, ${\bigcap }_{x\in X}F(x)\ne \mathrm{\varnothing }$. □

We now derive some general versions of minimax inequalities from Lemma 5.1.

Theorem 5.2 Let X, Y be compact subsets of linear topological spaces. $\phi :X\times Y\mapsto R$ satisfies the following conditions:

• (1) For any fixed $y\in Y$, $\phi (x,y)$ is lower semi-continuous with respect to x;

• (2) $s:X\mapsto 2^Y$ is an upper semi-continuous mapping with nonempty, closed and contractible values and for any finite subset $\{y_0,y_1,\dots ,y_n\}\subset Y$ and $x\in s(co\{y_0,y_1,\dots ,y_n\})$, $\phi (x,y_i)\le 0$ for some $i=0,1,\dots ,n$.

Then there exists $x^{\ast }\in X$, such that

$$\phi (x^{\ast },y)\le 0,\mathrm{\forall }y\in Y.$$

Proof The multi-valued mapping $F:Y\mapsto 2^X$ is defined as

$$F(y)=\{x\in X:\phi (x,y)\le 0\},\mathrm{\forall }y\in Y.$$

Condition (1) implies that F is closed-valued.

From condition (2), it is easy to check that for each finite subset $\{y_0,y_1,\dots ,y_n\}\subset Y$, F satisfies

$$s(co\{y_0,y_1,\dots ,y_n\})\subset \bigcup _{i=0}^{n}F(y_i).$$

In fact, for each $x\in s(co\{y_0,y_1,\dots ,y_n\})$, it follows from (2) that $\phi (x,y_i)\le 0$ for some $i=0,1,\dots ,n$, i.e., $x\in F(y_i)$ for some $i=0,1,\dots ,n$. Thus $x\in {\bigcup }_{i=0}^{n}F(y_i)$ and $s(co\{y_0,y_1,\dots ,y_n\})\subset {\bigcup }_{i=0}^{n}F(y_i)$.

By Lemma 5.1, we have ${\bigcap }_{y\in Y}F(y)\ne \mathrm{\varnothing }$. Then there exists some $x^{\ast }\in X$ such that $x^{\ast }\in {\bigcap }_{y\in Y}F(y)$, so that

$$\phi (x^{\ast },y)\le 0,\mathrm{\forall }y\in Y.$$

 □

Definition 5.3 Let Y be a subset of some linear topological space. A function $\phi :Y\mapsto R$ is said to be quasiconcave if, for each finite subset $\{y_0,y_1,\dots ,y_n\}\subset Y$, φ satisfies

$$\phi (y)\ge min\{\phi (y_0),\phi (y_1),\dots ,\phi (y_n)\},\mathrm{\forall }y\in co\{y_0,y_1,\dots ,y_n\}.$$

φ is said to be s-quasiconcave if there exists an upper semi-continuous mapping $s:Y\mapsto 2^X$ and for each finite subset $\{y_0,y_1,\dots ,y_n\}\subset Y$, φ satisfies

$$\phi (y)\ge min\{\phi (y_0),\phi (y_1),\dots ,\phi (y_n)\},\mathrm{\forall }y\in s(co\{y_0,y_1,\dots ,y_n\}).$$

Below, we present two forms of minimax inequalities.

Theorem 5.4 Let X, Y be compact subsets of linear topological spaces. If $\phi :X\times Y\mapsto R$ satisfies the following conditions:

• (1) For any fixed $y\in X$, $\phi (x,y)$ is lower semi-continuous respect to x;

• (2) $s:Y\mapsto 2^X$ is an upper semi-continuous mapping with nonempty, closed and contractible values, and for any fixed $x\in s(Y)$, $\phi (x,y)$ is quasiconcave with respect to y;

• (3) For any $y\in Y$ and $x\in s(y)$, $\phi (x,y)\le 0$.

Then there exists $x^{\ast }\in X$, such that

$$\phi (x^{\ast },y)\le 0,\mathrm{\forall }y\in Y.$$

Proof By Theorem 5.2, it remains to prove that for each finite subset $\{y_0,y_1,\dots ,y_n\}\subset Y$ and $x\in s(co\{y_0,y_1,\dots ,y_n\})$, $\phi (x,y_i)\le 0$ for each $i=0,1,\dots ,n$.

If not, there exists some $\overline{x}\in s(co\{y_0,y_1,\dots ,y_n\})$ such that $\phi (\overline{x},y_i)>0$ for each $i=0,1,\dots ,n$. From condition (2), it follows that $\phi (\overline{x},y)>0$ for all $y\in co\{y_0,y_1,\dots ,y_n\}$. Note that $\overline{x}\in s(co\{y_0,y_1,\dots ,y_n\})$. Then there exists some $\overline{y}\in co\{y_0,y_1,\dots ,y_n\}$ such that $\overline{x}\in s(\overline{y})$. It is immediate that $\phi (\overline{x},\overline{y})>0$, which is a contradiction with condition (3). The proof is complete. □

Theorem 5.4 generalizes the Ky Fan minimax inequality theorem to the case that φ is defined on the sets of two different linear topological spaces. We next present a minimax inequality theorem that φ is defined on the same set.

Theorem 5.5 Let X be a compact subset of some linear topological space. $\phi :X\times X\mapsto R$ satisfies the following conditions:

• (1) For any fixed $y\in X$, $\phi (x,y)$ is lower semi-continuous with respect to x;

• (2) $s:X\mapsto 2^X$ is an upper semi-continuous mapping with nonempty, closed and contractible values and for any fixed $x\in s(X)$, $\phi (x,y)$ is s-quasiconcave with respect to y;

• (3) $\phi (x,x)\le 0$, $\mathrm{\forall }x\in X$.

Then there exists $x^{\ast }\in X$ such that $\phi (x^{\ast },y)\le 0$ for all $y\in Y$.

Proof By Theorem 5.2, it remains to prove that for each finite subset $\{y_0,y_1,\dots ,y_n\}\subset Y$ and $x\in s(co\{x_0,x_1,\dots ,x_n\})$, $\phi (x,y_i)\le 0$ for each $i=0,1,\dots ,n$.

If not, there exists some $\overline{y}\in co\{y_0,y_1,\dots ,y_n\}$ and $\overline{x}\in s(\overline{y})$ such that $\phi (\overline{x},y_i)>0$ for each $i=0,1,\dots ,n$. Since $\phi (\overline{x},y)$ is s-quasiconcave with respect to y, it follows that $\phi (\overline{x},y)\ge min\{\phi (\overline{x},y_0),\phi (\overline{x},y_1),\dots ,\phi (\overline{x},y_n)\}>0$ for all $y\in s(co\{y_0,y_1,\dots ,y_n\})$. Note that $\overline{x}\in s(\overline{y})\subset s(co\{y_0,y_1,\dots ,y_n\})$. It is immediate that $\phi (\overline{x},\overline{x})>0$ which contradicts condition (3). By Theorem 5.2, the proof is complete. □

Further, we prove that condition (2) is necessary for the conclusion of Theorem 5.5 under a certain condition.

Theorem 5.6 Let X be a compact subset of linear topological space. $\phi :X\times X\mapsto R$ satisfies the following conditions:

• (1) For any fixed $y\in X$, $\phi (x,y)$ is lower semi-continuous with respect to x;

• (2) $\phi (x,x)=0$, $\mathrm{\forall }x\in X$.

Then there exists $x^{\ast }\in X$ such that $\phi (x^{\ast },y)\le 0$ for all $y\in Y$ if and only if there exists an upper semi-continuous mapping $s:X\mapsto 2^X$ with nonempty, closed and contractible values and for any fixed $x\in s(X)$, $\phi (x,y)$ is s-quasiconcave with respect to y.

Proof It only needs to prove the necessity. If there exists $x^{\ast }\in X$ such that

$$\phi (x^{\ast },y)\le 0,\mathrm{\forall }y\in Y.$$

Define $s:X\mapsto 2^X$ as

$$s(y)=\left\{x^{\ast }\right\},\mathrm{\forall }y\in Y.$$

It is clear that s is an upper semi-continuous mapping with nonempty, closed and contractible values.

On the other hand, for any fixed $x\in s(X)$, we have $y=x^{\ast }$. Let $\{y_0,y_1,\dots ,y_n\}\subset Y$. Note that $s(co\{y_0,y_1,\dots ,y_n\})=\{x^{\ast }\}$ and $\phi (x^{\ast },y)\le 0$ for all $y\in X$. We have $\phi (x^{\ast },y)=\phi (x^{\ast },x^{\ast })=0\ge min\{\phi (x^{\ast },y_0),\phi (x^{\ast },y_1),\dots ,\phi (x^{\ast },y_n)\}$ for all $y\in s(co\{y_0,y_1,\dots ,y_n\})$, so that $\phi (x,y)$ is s-quasiconcave with respect to y. The proof is complete. □

We can weaken the convexity condition of the function φ by choosing a proper $s:X\mapsto 2^X$. To see this, we observe the following example.

Example 5.7 Let $X=[0,1]\subset R$, $\phi :X\times X\mapsto R$ be a function defined by

$$\phi (x,y)=\{\begin{array}{cc}0\hfill & \mathrm{\forall }x\le y;\hfill \\ xsin2\pi (x-y),\hfill & \mathrm{\forall }x>y.\hfill \end{array}$$

Now we check that φ satisfies all conditions of Theorem 5.5.

$s:X\mapsto 2^X$ is defined as

$$s(y)=\{0\},\mathrm{\forall }y\in Y.$$

It is easy to check that φ satisfies (1) and (3) of Theorem 5.5. It remains to show that (2) holds. For each $x\in s(X)$, it follows from the definition of s that $x=0$. Let $\{y_0,y_1,\dots ,y_n\}\subset Y$, and let $y\in s(co\{y_0,y_1,\dots ,y_n\})$; we have $\phi (0,y)=\phi (0,0)=0\ge \phi (0,y_i)$, so that $\phi (0,y)\ge min\{\phi (0,y_0),\phi (0,y_1),\dots ,\phi (0,y_n)\}$. Hence $\phi (x,y)$ is s-quasiconcave with respect to y.

On the other hand, we observe that $\phi (1,y)$ is neither quasiconcave nor quasiconvex with respect to y.

Since we can apply minimax inequalities to prove the existence of Nash equilibrium points in non-cooperative games, Theorems 5.2, 5.4 and 5.5 enable us to discuss the existence of Nash equilibrium under some weaker convexity conditions.