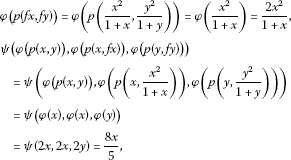Fixed point theory of cyclical generalized contractive conditions in partial metric spaces

Abstract

The purpose of this paper is to study fixed point theorems for a mapping satisfying the cyclical generalized contractive conditions in complete partial metric spaces. Our results generalize or improve many recent fixed point theorems in the literature.

MSC:47H10, 54C60, 54H25, 55M20.

1 Introduction and preliminaries

Throughout this paper, by ${\mathbb{R}}^{+}$, we denote the set of all nonnegative real numbers, while ℕ is the set of all natural numbers. Let $(X,d)$ be a metric space, D be a subset of X and $f:D\to X$ be a map. We say f is contractive if there exists $\alpha \in [0,1)$ such that for all $x,y\in D$,

$$d(fx,fy)\le \alpha \cdot d(x,y).$$

The well-known Banach fixed point theorem asserts that if $D=X$, f is contractive and $(X,d)$ is complete, then f has a unique fixed point in X. It is well known that the Banach contraction principle [1] is a very useful and classical tool in nonlinear analysis. Also, this principle has many generalizations. For instance, in 1969, Boyd and Wong [2] introduced the notion of Φ-contraction. A mapping $f:X\to X$ on a metric space is called Φ-contraction if there exists an upper semi-continuous function $\mathrm{\Phi }:[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ such that

$$d(fx,fy)\le \mathrm{\Phi }(d(x,y))\text{for all }x,y\in X.$$

In 1994, Mattews [3] introduced the following notion of partial metric spaces.

Definition 1 [3] A partial metric on a nonempty set X is a function $p:X\times X\to {\mathbb{R}}^{+}$ such that for all $x,y,z\in X$,

(p₁) $x=y$ if and only if $p(x,x)=p(x,y)=p(y,y)$;

(p₂) $p(x,x)\le p(x,y)$;

(p₃) $p(x,y)=p(y,x)$;

(p₄) $p(x,y)\le p(x,z)+p(z,y)-p(z,z)$.

A partial metric space is a pair $(X,p)$ such that X is a nonempty set and p is a partial metric on X.

Remark 1 It is clear that if $p(x,y)=0$, then from (p₁) and (p₂), $x=y$. But if $x=y$, $p(x,y)$ may not be 0.

Each partial metric p on X generates a ${\mathcal{T}}_0$ topology ${\tau }_p$ on X which has as a base the family of open p-balls $\{B_p(x,\gamma ):x\in X,\gamma >0\}$, where $B_p(x,\gamma )=\{y\in X:p(x,y)<p(x,x)+\gamma \}$ for all $x\in X$ and $\gamma >0$. If p is a partial metric on X, then the function $d_p:X\times X\to {\mathbb{R}}^{+}$ given by

$$d_p(x,y)=2p(x,y)-p(x,x)-p(y,y)$$

is a metric on X.

We recall some definitions of a partial metric space as follows.

Definition 2 [3]

Let $(X,p)$ be a partial metric space. Then

• (1) a sequence $\{x_n\}$ in a partial metric space $(X,p)$ converges to $x\in X$ if and only if $p(x,x)={lim}_{n\to \mathrm{\infty }}p(x,x_n)$;

• (2) a sequence $\{x_n\}$ in a partial metric space $(X,p)$ is called a Cauchy sequence if and only if ${lim}_{m,n\to \mathrm{\infty }}p(x_m,x_n)$ exists (and is finite);

• (3) a partial metric space $(X,p)$ is said to be complete if every Cauchy sequence $\{x_n\}$ in X converges, with respect to ${\tau }_p$, to a point $x\in X$ such that $p(x,x)={lim}_{m,n\to \mathrm{\infty }}p(x_m,x_n)$;

• (4) a subset A of a partial metric space $(X,p)$ is closed if whenever $\{x_n\}$ is a sequence in A such that $\{x_n\}$ converges to some $x\in X$, then $x\in A$.

Remark 2 The limit in a partial metric space is not unique.

Lemma 1 [3, 4]

• (a) $\{x_n\}$ is a Cauchy sequence in a partial metric space $(X,p)$ if and only if it is a Cauchy sequence in the metric space $(x,d_p)$;

• (b) a partial metric space $(X,p)$ is complete if and only if the metric space $(X,d_p)$ is complete. Furthermore, ${lim}_{n\to \mathrm{\infty }}{d}_p(x_n,x)=0$ if and only if $p(x,x)={lim}_{n\to \mathrm{\infty }}p(x_n,x)={lim}_{n\to \mathrm{\infty }}p(x_n,x_m)$.

In 2003, Kirk, Srinivasan and Veeramani [5] introduced the following notion of the cyclic representation.

Definition 3 [5]

Let X be a nonempty set, $m\in \mathbb{N}$ and $f:X\to X$ be an operator. Then $X={\bigcup }_{i=1}^m{A}_i$ is called a cyclic representation of X with respect to f if

• (1) $A_i$, $i=1,2,\dots ,m$ are nonempty subsets of X;

• (2) $f(A_1)\subset A_2,f(A_2)\subset A_3,\dots ,f(A_{m-1})\subset A_m,f(A_m)\subset A_1$.

Kirk, Srinivasan and Veeramani [5] also proved the following theorem.

Theorem 1 [5]

Let $(X,d)$ be a complete metric space, $m\in \mathbb{N}$, $A_1,A_2,\dots ,A_m$, be closed nonempty subsets of X and $X={\bigcup }_{i=1}^m{A}_i$. Suppose that f satisfies the following condition:

$$d(fx,fy)\le \psi (d(x,y)),\mathit{\text{for all}}x\in A_i,y\in A_{i+1},i\in \{1,2,\dots ,m\},$$

where $\psi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ is upper semi-continuous from the right and $0\le \psi (t)<t$ for $t>0$. Then f has a fixed point $z\in {\bigcap }_{i=1}^n{A}_i$.

Recently, the fixed theorems for an operator $f:X\to X$ defined on a metric space X with a cyclic representation of X with respect to f have appeared in the literature (see, e.g., [6–8]). In 2010, Pǎcurar and Rus [7] introduced the following notion of a cyclic weaker φ-contraction.

Definition 4 [7]

Let $(X,d)$ be a metric space, $m\in \mathbb{N}$, $A_1,A_2,\dots ,A_m$ be closed nonempty subsets of X and $X={\bigcup }_{i=1}^m{A}_i$. An operator $f:X\to X$ is called a cyclic weaker φ-contraction if

• (1) $X={\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of X with respect to f;

• (2) there exists a continuous, non-decreasing function $\phi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ with $\phi (t)>0$ for $t\in (0,\mathrm{\infty })$ and $\phi (0)=0$ such that

  $$d(fx,fy)\le d(x,y)-\phi (d(x,y))$$

for any $x\in A_i$, $y\in A_{i+1}$, $i=1,2,\dots ,m$, where $A_{m+1}=A_1$.

And Pǎcurar and Rus [7] proved the following main theorem.

Theorem 2 [7]

Let $(X,d)$ be a complete metric space, $m\in \mathbb{N}$, $A_1,A_2,\dots ,A_m$ be closed nonempty subsets of X and $X={\bigcup }_{i=1}^m{A}_i$. Suppose that f is a cyclic weaker φ-contraction. Then f has a fixed point $z\in {\bigcap }_{i=1}^n{A}_i$.

In the recent years, fixed point theory has developed rapidly on cyclic contraction mappings, see [9–15].

The purpose of this paper is to study fixed point theorems for a mapping satisfying the cyclical generalized contractive conditions in complete partial metric spaces. Our results generalize or improve many recent fixed point theorems in the literature.

2 Fixed point theorems (I)

In the section, we denote by Ψ the class of functions $\psi :{{\mathbb{R}}^{+}}^3\to {\mathbb{R}}^{+}$ satisfying the following conditions:

(${\psi }_1$) ψ is an increasing and continuous function in each coordinate;

(${\psi }_2$) for $t\in {\mathbb{R}}^{+}$, $\psi (t,t,t)\le t$, $\psi (t,0,0)\le t$ and $\psi (0,0,t)\le t$.

Next, we denote by Θ the class of functions $\phi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ satisfying the following conditions:

(${\phi }_1$) φ is continuous and non-decreasing;

(${\phi }_2$) for $t>0$, $\phi (t)>0$ and $\phi (0)=0$.

And we denote by Φ the class of functions $\varphi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ satisfying the following conditions:

(${\varphi }_1$) ϕ is continuous;

(${\varphi }_2$) for $t>0$, $\varphi (t)>0$ and $\varphi (0)=0$.

We now state a new notion of cyclic $\mathcal{CW}$-contractions in partial metric spaces as follows.

Definition 5 Let $(X,p)$ be a partial metric space, $m\in \mathbb{N}$, $A_1,A_2,\dots ,A_m$ be nonempty subsets of X and $Y={\bigcup }_{i=1}^m{A}_i$. An operator $f:Y\to Y$ is called a cyclic $\mathcal{CW}$-contraction if

• (1) ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of Y with respect to f;

• (2) for any $x\in A_i$, $y\in A_{i+1}$, $i=1,2,\dots ,m$,

  $$\phi (p(fx,fy))\le \psi (\phi (p(x,y)),\phi (p(x,fx)),\phi (p(y,fy)))-\varphi (M(x,y)),$$

  (2.1)

where $\psi \in \mathrm{\Psi }$, $\phi \in \mathrm{\Theta }$, $\varphi \in \mathrm{\Phi }$, and $M(x,y)=max\{p(x,y),p(x,fx),p(y,fy)\}$.

Theorem 3 Let $(X,p)$ be a complete partial metric space, $m\in \mathbb{N}$, $A_1,A_2,\dots ,A_m$ be nonempty closed subsets of X and $Y={\bigcup }_{i=1}^m{A}_i$. Let $f:Y\to Y$ be a cyclic $\mathcal{CW}$-contraction. Then f has a unique fixed point $z\in {\bigcap }_{i=1}^m{A}_i$.

Proof Given $x_0$ and let $x_{n+1}=f{x}_n=f^n{x}_0$ for $n=0,1,2,\dots$ . If there exists $n_0\in \mathbb{N}$ such that $x_{n_0+1}=x_{n_0}$, then we finished the proof. Suppose that $x_{n+1}\ne x_n$ for any $n=0,1,2,\dots$ . Notice that for any $n\ge 0$, there exists $i_n\in \{1,2,\dots ,m\}$ such that $x_n\in A_{i_n}$ and $x_{n+1}\in A_{i_n+1}$.

Step 1. We will prove that

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,x_{n+1})=0,\text{that is},\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_n,x_{n+1})=0.$$

Using (2.1), we have

$$\begin{array}{rcl}\phi (p(x_n,x_{n+1}))& =& \phi (p(f{x}_{n-1},f{x}_n))\\ \le & \psi (\phi (p(x_{n-1},x_n)),\phi (p(x_{n-1},f{x}_{n-1})),\phi (p(x_n,f{x}_n)))-\varphi (M(x_{n-1},x_n))\\ =& \psi (\phi (p(x_{n-1},x_n)),\phi (p(x_{n-1},x_n)),\phi (p(x_n,x_{n+1})))-\varphi (M(x_{n-1},x_n)),\end{array}$$

where

$$\begin{array}{rl}M(x_{n-1},x_n)& =max\{p(x_{n-1},x_n),p(x_{n-1},f{x}_{n-1}),p(x_n,f{x}_n)\}\\ =max\{p(x_{n-1},x_n),p(x_{n-1},x_n),p(x_n,x_{n+1})\}.\end{array}$$

If $M(x_{n-1},x_n)=p(x_n,x_{n+1})$, then

$$\begin{array}{rcl}\phi (p(x_n,x_{n+1}))& \le & \psi (\phi (p(x_n,x_{n+1})),\phi (p(x_n,x_{n+1})),\phi (p(x_n,x_{n+1})))-\varphi (p(x_n,x_{n+1}))\\ \le & \phi (p(x_n,x_{n+1}))-\varphi (p(x_n,x_{n+1})),\end{array}$$

which implies that $\varphi (p(x_n,x_{n+1}))=0$, and hence $p(x_n,x_{n+1})=0$. This contradicts our initial assumption.

From the above argument, we have that for each $n\in \mathbb{N}$,

$$\phi (p(x_n,x_{n+1}))\le \phi (p(x_{n-1},x_n))-\varphi (p(x_{n-1},x_n)),$$

(2.2)

and

$$p(x_n,x_{n+1})<p(x_{n-1},x_n).$$

And since the sequence $\{p(x_n,x_{n+1})\}$ is decreasing, it must converge to some $\eta \ge 0$. Taking limit as $n\to \mathrm{\infty }$ in (2.2) and by the continuity of φ and ϕ, we get

$$\phi (\eta )\le \phi (\eta )-\varphi (\eta ),$$

and so we conclude that $\varphi (\eta )=0$ and $\eta =0$. Thus, we have

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,x_{n+1})=0.$$

(2.3)

By (p₂), we also have

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,x_n)=0.$$

(2.4)

Since $d_p(x,y)\le 2p(x,y)-p(x,x)-p(y,y)$ for all $x,y\in X$, using (2.3) and (2.4), we obtain that

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_n,x_{n+1})=0.$$

(2.5)

Step 2. We show that $\{x_n\}$ is a Cauchy sequence in the metric space $(Y,d_p)$. We claim that the following result holds.

Claim For every $\epsilon >0$, there exists $n\in \mathbb{N}$ such that if $r,q\ge n$ with $r-q=1modm$, then $d_p(x_r,x_q)<\epsilon$.

Suppose the above statement is false. Then there exists $ϵ>0$ such that for any $n\in \mathbb{N}$, there are $r_n,q_n\in \mathbb{N}$ with $r_n>q_n\ge n$ with $r_n-q_n=1modm$ satisfying

$$d_p(x_{q_n},x_{r_n})\ge ϵ.$$

Now, we let $n>2m$. Then corresponding to $q_n\ge n$ use, we can choose $r_n$ in such a way it is the smallest integer with $r_n>q_n\ge n$ satisfying $r_n-q_n=1modm$ and $d_p(x_{q_n},x_{r_n})\ge ϵ$. Therefore, $d_p(x_{q_n},x_{r_n-m})\le ϵ$ and

$$\begin{array}{rl}ϵ& \le d_p(x_{q_n},x_{r_n})\\ \le d_p(x_{q_n},x_{r_n-m})+\sum _{i=1}^m{d}_p(x_{r_{n-i}},x_{r_{n-i+1}})\\ <ϵ+\sum _{i=1}^m{d}_p(x_{r_{n-i}},x_{r_{n-i+1}}).\end{array}$$

Letting $n\to \mathrm{\infty }$, we obtain that

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_{q_n},x_{r_n})=ϵ.$$

(2.6)

On the other hand, we can conclude that

$$\begin{array}{rl}ϵ& \le d_p(x_{q_n},x_{r_n})\\ \le d_p(x_{q_n},x_{q_{n+1}})+d_p(x_{q_{n+1}},x_{r_{n+1}})+d_p(x_{r_{n+1}},x_{r_n})\\ \le d_p(x_{q_n},x_{q_{n+1}})+d_p(x_{q_{n+1}},x_{q_n})+d_p(x_{q_n},x_{r_n})+d_p(x_{r_n},x_{r_{n+1}})+d_p(x_{r_{n+1}},x_{r_n}).\end{array}$$

Letting $n\to \mathrm{\infty }$, we obtain that

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_{q_{n+1}},x_{r_{n+1}})=ϵ.$$

(2.7)

Since $d_p(x,y)=2p(x,y)-p(x,x)-p(y,y)$ and using (2.4), (2.6) and (2.7), we have that

$$\underset{n\to \mathrm{\infty }}{lim}p(x_{q_n},x_{r_n})=\frac{ϵ}{2},$$

(2.8)

and

$$\underset{n\to \mathrm{\infty }}{lim}p(x_{q_{n+1}},x_{r_{n+1}})=\frac{ϵ}{2}.$$

(2.9)

Since $x_{q_n}$ and $x_{r_n}$ lie in different adjacently labeled sets $A_i$ and $A_{i+1}$ for certain $1\le i\le m$, by using the fact that f is a cyclic $\mathcal{CW}$-contraction, we have

$$\begin{array}{rcl}\phi (p(f{x}_{q_n+1},f{x}_{r_n+1}))& =& \phi (p(f{x}_{q_n},f{x}_{r_n}))\\ \le & \psi (\phi (p(x_{q_n},x_{r_n})),\phi (p(x_{q_n},f{x}_{q_n})),\phi (p(x_{r_n},f{x}_{r_n})))\\ -\varphi (M(x_{q_n},x_{r_n}))\\ =& \psi (\phi (p(x_{q_n},x_{r_n})),\phi (p(x_{q_n},x_{q_n+1})),\phi (p(x_{r_n},x_{r_n+1})))\\ -\varphi (M(x_{q_n},x_{r_n})),\end{array}$$

where

$$M(x_{q_n},x_{r_n})=max\{p(x_{q_n},x_{r_n}),p(x_{q_n},x_{q_n+1}),p(x_{r_n},x_{r_n+1})\}.$$

Thus, letting $n\to \mathrm{\infty }$, we can conclude that

$$\phi \left(\frac{ϵ}{2}\right)\le \psi (\phi \left(\frac{ϵ}{2}\right),\phi (0),\phi (0))-\varphi \left(\frac{ϵ}{2}\right)\le \phi \left(\frac{ϵ}{2}\right)-\varphi \left(\frac{ϵ}{2}\right),$$

which implies $\varphi (\frac{ϵ}{2})=0$, that is, $ϵ=0$. So, we get a contradiction. Therefore, our claim is proved.

In the sequel, we will show that $\{x_n\}$ is a Cauchy sequence in the metric space $(Y,d_p)$. Let $\epsilon >0$ be given. By our claim, there exists $n_1\in \mathbb{N}$ such that if $r,q\ge n_1$ with $r-q=1modm$, then

$$d_p(x_r,x_q)\le \frac{\epsilon }{2}.$$

Since ${lim}_{n\to \mathrm{\infty }}{d}_p(x_n,x_{n+1})=0$, there exists $n_2\in \mathbb{N}$ such that

$$d_p(x_n,x_{n+1})\le \frac{\epsilon }{2m}$$

for any $n\ge n_2$.

Let $r,q\ge max\{n_1,n_2\}$ and $r>q$. Then there exists $k\in \{1,2,\dots ,m\}$ such that $r-q=kmodm$. Therefore, $r-q+j=1modm$ for $j=m-k+1$, and so we have

$$\begin{array}{rl}{d}_p(x_q,x_r)& \le d_p(x_q,x_{r+j})+d_p(x_{r+j},x_{r+j-1})+\cdots +d_p(x_{r-1},x_r)\\ \le \frac{\epsilon }{2}+j\times \frac{\epsilon }{2m}\\ \le \frac{\epsilon }{2}+m\times \frac{\epsilon }{2m}=\epsilon .\end{array}$$

Thus, $\{x_n\}$ is a Cauchy sequence in the metric space $(Y,d_p)$.

Step 3. We show that f has a fixed point ν in ${\bigcap }_{i=1}^m{A}_i$.

Since Y is closed, the subspace $(Y,p)$ is complete. Then from Lemma 1, we have that $(Y,d_p)$ is complete. Thus, there exists $\nu \in X$ such that

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_n,\nu )=0.$$

And it follows from Lemma 1 that we have

$$p(\nu ,\nu )=\underset{n\to \mathrm{\infty }}{lim}p(x_n,\nu )=\underset{n,m\to \mathrm{\infty }}{lim}p(x_n,x_m).$$

(2.10)

On the other hand, since the sequence $\{x_n\}$ is a Cauchy sequence in the metric space $(Y,d_p)$, we also have

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_n,x_m)=0.$$

Since $d_p(x,y)=2p(x,y)-p(x,x)-p(y,y)$, we can deduce that

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,x_m)=0.$$

(2.11)

Since $Y={\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of X with respect to f, the sequence $\{x_n\}$ has infinite terms in each $A_i$ for $i\in \{1,2,\dots ,m\}$. Now, for all $i=1,2,\dots ,m$, we may take a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ with $x_{n_k}\in A_{i-1}$ and also all converge to ν. Using (2.10) and (2.11), we have

$$p(\nu ,\nu )=\underset{n\to \mathrm{\infty }}{lim}p(x_n,\nu )=\underset{n\to \mathrm{\infty }}{lim}p(x_{n_k},\nu )=0.$$

By (2.1),

$$\begin{array}{rl}\phi (p(x_{n_{k+1}},f\nu ))& =\phi (p(f{x}_{n_k},f\nu ))\\ \le \psi (\phi (p(x_{n_k},\nu )),\phi (p(x_{n_k},f{x}_{n_k})),\phi (p(\nu ,f\nu )))-\varphi (M(x_{n_k},\nu ))\\ =\psi (\phi (p(x_{n_k},\nu )),\phi (p(x_{n_k},x_{n_k+1})),\phi (p(\nu ,f\nu )))-\varphi (M(x_{n_k},\nu )),\end{array}$$

where

$$M(x_{n_k},\nu )=max\{p(x_{n_k},\nu ),p(x_{n_k},x_{n_k+1}),p(\nu ,f\nu )\}.$$

Letting $k\to \mathrm{\infty }$, we have

$$\begin{array}{rl}\phi (p(\nu ,f\nu ))& \le \psi (\phi (0),\phi (0),\phi (p(\nu ,f\nu )))-\varphi (p(\nu ,f\nu ))\\ \le \phi (p(\nu ,f\nu ))-\varphi (p(\nu ,f\nu )),\end{array}$$

which implies $\varphi (p(\nu ,f\nu ))=0$, that is, $p(\nu ,f\nu )=0$. So, $\nu =f\nu$.

Step 4. Finally, to prove the uniqueness of the fixed point, suppose that μ, ν are fixed points of f. Then using the inequality (2.1), we obtain that

$$\begin{array}{rcl}\phi (p(\mu ,\nu ))& =& \phi (p(f\mu ,f\nu ))\le \psi (\phi (p(\mu ,\nu )),\phi (p(\mu ,f\mu )),\phi (p(\nu ,f\nu )))\\ -\varphi (M(\mu ,\nu )),\end{array}$$

where

$$M(\mu ,\nu )=max\{p(\mu ,\nu ),p(\mu ,f\mu ),p(\nu ,f\nu )\}=p(\mu ,\nu ).$$

So, we also deduce that

$$\begin{array}{rl}\phi (p(\mu ,\nu ))& \le \psi \left(\phi (p(\mu ,\nu ),0,0)\right)\\ \le \phi (p(\mu ,\nu ))-\varphi (p(\mu ,\nu )),\end{array}$$

which implies that $\varphi (p(\mu ,\nu ))=0$, and hence $p(\mu ,\nu )=0$, that is, $\mu =\nu$. So, we complete the proof.  □

The following provides an example for Theorem 3.

Example 1 Let $X=[0,1]$ and $A=[0,1]$, $B=[0,\frac{1}{2}]$, $C=[0,\frac{1}{4}]$. We define the partial metric p on X by

$$p(x,y)=max\{x,y\}\text{for all }x,y\in X,$$

and define the function $f:X\to X$ by

$$f(x)=\frac{x^2}{1+x}\text{for all }x\in X.$$

Now, we let $\phi ,\varphi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ and $\psi :{{\mathbb{R}}^{+}}^3\to {\mathbb{R}}^{+}$ be

$$\phi (t)=2t,\varphi (t)=\frac{2t}{5(1+t)}\text{and}\psi (t)=\frac{4}{5}\cdot max\{t_1,t_2,t_3\}.$$

Then f is a cyclic $\mathcal{CW}$-contraction and 0 is the unique fixed point.

Proof We claim that f is a cyclic $\mathcal{CW}$-contraction.

• (1) Note that $f(A)=[0,\frac{1}{2}]\subset B$, $f(B)=[0,\frac{1}{6}]\subset C$ and $f(C)=[0,\frac{1}{20}]\subset A$. Thus, $A\cup B\cup C$ is a cyclic representation of X with respect to f;

• (2) For $x\in A$ and $y\in B$ (or, $x\in B$ and $y\in C$), without loss of generality, we may assume that $x\ge y$, then we have

  

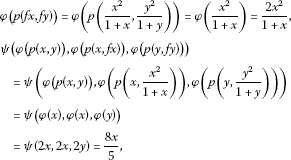
and

Since

$$\frac{2x^2}{1+x}\le \frac{8x}{5}-\frac{2x}{5(1+x)},$$

we have

$$\begin{array}{rcl}\phi (p(fx,fy))& \le & \psi (\phi (p(x,y)),\phi (p(x,fx)),\phi (p(y,fy)))\\ -\varphi (max\{p(x,y),p(x,fx),p(y,fy)\}).\end{array}$$

On the other hand, for $x\in C$ and $y\in A$, without loss of generality, we may assume that $x\le y$, then it is easy to get the above inequality.

Note that Example 1 satisfies all of the hypotheses of Theorem 3, and we get that 0 is the unique fixed point. □

3 Fixed point theorems (II)

In this article, we also recall the notion of a Meir-Keeler function (see [16]). A function $\varphi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ is said to be a Meir-Keeler function if for each $\eta >0$, there exists $\delta >0$ such that for $t\in [0,\mathrm{\infty })$ with $\eta \le t<\eta +\delta$, we have $\varphi (t)<\eta$. We now introduce a new notion of a weaker Meir-Keeler function $\varphi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ in a partial metric space $(X,p)$ as follows.

Definition 6 Let $(X,p)$ be a partial metric space. We call $\varphi :[0,\mathrm{\infty })\to [0,\mathrm{\infty })$ a weaker Meir-Keeler function in X if for each $\eta >0$, there exists $\delta >0$ such that for $x,y\in X$ with $\eta \le p(x,y)<\eta +\delta$, there exists $n_0\in \mathbb{N}$ such that ${\varphi }^{n_0}(p(x,y))<\eta$.

In the section, we denote by Φ the class of weaker Meir-Keeler functions $\varphi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ in a partial metric space in $(X,p)$ satisfying the following conditions:

(${\varphi }_1$) $\varphi (t)>0$ for $t>0$, $\varphi (0)=0$;

(${\varphi }_2$) ${\{{\varphi }^n(t)\}}_{n\in \mathbb{N}}$ is decreasing;

(${\varphi }_3$) for $t_n\in [0,\mathrm{\infty })$,

• (a) if ${lim}_{n\to \mathrm{\infty }}{t}_n=\gamma >0$, then ${lim}_{n\to \mathrm{\infty }}\varphi (t_n)<\gamma$ and

• (b) if ${lim}_{n\to \mathrm{\infty }}{t}_n=0$, then ${lim}_{n\to \mathrm{\infty }}\varphi (t_n)=0$.

And we denote by the class Ψ of functions $\psi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ a continuous function satisfying $\psi (t)>0$ for $t>0$, $\psi (0)=0$.

First, we state a new notion of cyclic $\mathcal{MK}$-contractions in partial metric spaces as follows.

Definition 7 Let $(X,p)$ be a partial metric space, $m\in \mathbb{N}$, $A_1,A_2,\dots ,A_m$ be nonempty subsets of X and $Y={\bigcup }_{i=1}^m{A}_i$. An operator $f:Y\to Y$ is called a cyclic $\mathcal{MK}$-contraction if

• (1) ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of Y with respect to f;

• (2) for any $x\in A_i$, $y\in A_{i+1}$, $i=1,2,\dots ,m$,

  $$p(fx,fy)\le \varphi (p(x,y))-\psi (p(x,y)),$$

  (3.1)

where $A_{m+1}=A_1$, $\varphi \in \mathrm{\Phi }$ and $\psi \in \mathrm{\Psi }$.

Theorem 4 Let $(X,p)$ be a complete partial metric space, $m\in \mathbb{N}$, $A_1,A_2,\dots ,A_m$ be nonempty closed subsets of X and $Y={\bigcup }_{i=1}^m{A}_i$. Let $f:Y\to Y$ be a cyclic $\mathcal{MK}$-contraction. Then f has a unique fixed point $z\in {\bigcap }_{i=1}^m{A}_i$.

Proof Given $x_0$ and let $x_{n+1}=f{x}_n=f^n{x}_0$, for $n=0,1,2,\dots$ . If there exists $n_0\in \mathbb{N}$ such that $x_{n_0+1}=x_{n_0}$, then we finished the proof. Suppose that $x_{n+1}\ne x_n$ for any $n=0,1,2,\dots$ . Notice that for any $n\ge 0$, there exists $i_n\in \{1,2,\dots ,m\}$ such that $x_n\in A_{i_n}$ and $x_{n+1}\in A_{i_n+1}$. Then by (3.1), we have

$$p(x_n,x_{n+1})=p(f{x}_{n-1},f{x}_n)\le \varphi (p(x_{n-1},x_n))-\psi (p(x_{n-1},x_n)).$$

Step 1. We will prove that

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,x_{n+1})=0,\text{that is},\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_n,x_{n+1})=0.$$

Since f is a cyclic $\mathcal{MK}$-contraction, we can conclude that

$$\begin{array}{rl}p(x_n,x_{n+1})& \le \varphi (p(x_{n-1},x_n))\\ \le \varphi (\varphi (p(x_{n-2},x_{n-1}))={\varphi }^2(p(x_{n-2},x_{n-1}))\\ \le \cdots \\ \le {\varphi }^n(p(x_0,x_1)).\end{array}$$

Since ${\{{\varphi }^n(p(x_0,x_1))\}}_{n\in \mathbb{N}}$ is decreasing, it must converge to some $\eta \ge 0$. We claim that $\eta =0$. On the contrary, assume that $0<\eta$. Then by the definition of a weaker Meir-Keeler function ϕ, there exists $\delta >0$ such that for $x_0,x_1\in X$ with $\eta \le p(x_0,x_1)<\delta +\eta$, there exists $n_0\in \mathbb{N}$ such that ${\varphi }^{n_0}(p(x_0,x_1))<\eta$. Since ${lim}_{n\to \mathrm{\infty }}{\varphi }^n(p(x_0,x_1))=\eta$, there exists $k_0\in \mathbb{N}$ such that $\eta \le {\varphi }^k(p(x_0,x_1))<\delta +\eta$, for all $k\ge k_0$. Thus, we conclude that ${\varphi }^{k_0+n_0}(p(x_0,x_1))<\eta$. So, we get a contradiction. Therefore, ${lim}_{n\to \mathrm{\infty }}{\varphi }^n(p(x_0,x_1))=0$, and so we have

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,x_{n+1})=0.$$

(3.2)

By (p₂), we also have

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,x_n)=0.$$

(3.3)

Since $d_p(x,y)\le 2p(x,y)-p(x,x)-p(y,y)$ for all $x,y\in X$, using (3.2) and (3.3), we obtain that

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_n,x_{n+1})=0.$$

(3.4)

Step 2. We show that $\{x_n\}$ is a Cauchy sequence in the metric space $(Y,d_p)$. We claim that the following result holds.

Claim For every $\epsilon >0$, there exists $n\in \mathbb{N}$ such that if $r,q\ge n$ with $r-q=1modm$, then $d_p(x_r,x_q)<\epsilon$.

Suppose the above statement is false. Then there exists $ϵ>0$ such that for any $n\in \mathbb{N}$, there are $r_n,q_n\in \mathbb{N}$ with $r_n>q_n\ge n$ with $r_n-q_n=1modm$ satisfying

$$d_p(x_{q_n},x_{r_n})\ge ϵ.$$

Now, we let $n>2m$. Then corresponding to $q_n\ge n$ use, we can choose $r_n$ in such a way it is the smallest integer with $r_n>q_n\ge n$ satisfying $r_n-q_n=1modm$ and $d_p(x_{q_n},x_{r_n})\ge ϵ$. Therefore, $d_p(x_{q_n},x_{r_n-m})\le ϵ$ and

$$\begin{array}{rl}ϵ& \le d_p(x_{q_n},x_{r_n})\\ \le d_p(x_{q_n},x_{r_n-m})+\sum _{i=1}^m{d}_p(x_{r_{n-i}},x_{r_{n-i+1}})\\ <ϵ+\sum _{i=1}^m{d}_p(x_{r_{n-i}},x_{r_{n-i+1}}).\end{array}$$

Letting $n\to \mathrm{\infty }$, we obtain that

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_{q_n},x_{r_n})=ϵ.$$

(3.5)

On the other hand, we can conclude that

$$\begin{array}{rl}ϵ& \le d_p(x_{q_n},x_{r_n})\\ \le d_p(x_{q_n},x_{q_{n+1}})+d_p(x_{q_{n+1}},x_{r_{n+1}})+d_p(x_{r_{n+1}},x_{r_n})\\ \le d_p(x_{q_n},x_{q_{n+1}})+d_p(x_{q_{n+1}},x_{q_n})+d_p(x_{q_n},x_{r_n})+d_p(x_{r_n},x_{r_{n+1}})+d_p(x_{r_{n+1}},x_{r_n}).\end{array}$$

Letting $n\to \mathrm{\infty }$, we obtain that

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_{q_{n+1}},x_{r_{n+1}})=ϵ.$$

(3.6)

Since $d_p(x,y)=2p(x,y)-p(x,x)-p(y,y)$ and using (3.5) and (3.6), we have that

$$\underset{n\to \mathrm{\infty }}{lim}p(x_{q_n},x_{r_n})=\frac{ϵ}{2},$$

(3.7)

and

$$\underset{n\to \mathrm{\infty }}{lim}p(x_{q_{n+1}},x_{r_{n+1}})=\frac{ϵ}{2}.$$

(3.8)

Since $x_{q_n}$ and $x_{r_n}$ lie in different adjacently labeled sets $A_i$ and $A_{i+1}$ for certain $1\le i\le m$, by using the fact that f is a cyclic $\mathcal{MK}$-contraction, we have

$$p(x_{q_{n+1}},x_{r_{n+1}})=p(f{x}_{q_n},f{x}_{r_n})\le \varphi (p(x_{q_n},x_{r_n}))-\psi (p(x_{q_n},x_{r_n})).$$

Letting $n\to \mathrm{\infty }$, by using the condition ${\varphi }_3$ of the function ϕ, we obtain that

$$\frac{ϵ}{2}\le \frac{ϵ}{2}-\psi \left(\frac{ϵ}{2}\right),$$

and consequently, $\psi (\frac{ϵ}{2})=0$. By the definition of a function ψ, we get $ϵ=0$ which is a contraction. Therefore, our claim is proved.

In the sequel, we will show that $\{x_n\}$ is a Cauchy sequence in the metric space $(Y,d_p)$. Let $\epsilon >0$ be given. By our claim, there exists $n_1\in \mathbb{N}$ such that if $r,q\ge n_1$ with $r-q=1modm$, then

$$d_p(x_r,x_q)\le \frac{\epsilon }{2}.$$

Since ${lim}_{n\to \mathrm{\infty }}{d}_p(x_n,x_{n+1})=0$, there exists $n_2\in \mathbb{N}$ such that

$$d_p(x_n,x_{n+1})\le \frac{\epsilon }{2m}$$

for any $n\ge n_2$.

Let $r,q\ge max\{n_1,n_2\}$ and $r>q$. Then there exists $k\in \{1,2,\dots ,m\}$ such that $r-q=kmodm$. Therefore, $r-q+j=1modm$ for $j=m-k+1$, and so we have

$$\begin{array}{rl}{d}_p(x_q,x_r)& \le d_p(x_q,x_{r+j})+d_p(x_{r+j},x_{r+j-1})+\cdots +d_p(x_{r-1},x_r)\\ \le \frac{\epsilon }{2}+j\times \frac{\epsilon }{2m}\\ \le \frac{\epsilon }{2}+m\times \frac{\epsilon }{2m}=\epsilon .\end{array}$$

Thus, $\{x_n\}$ is a Cauchy sequence in the metric space $(Y,d_p)$.

Step 3. We show that f has a fixed point ν in ${\bigcap }_{i=1}^m{A}_i$.

Since Y is closed, the subspace $(Y,p)$ is complete. Then from Lemma 1, we have that $(Y,d_p)$ is complete. Thus, there exists $\nu \in X$ such that

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_n,\nu )=0.$$

And it follows from Lemma 1 that we have

$$p(\nu ,\nu )=\underset{n\to \mathrm{\infty }}{lim}p(x_n,\nu )=\underset{n,m\to \mathrm{\infty }}{lim}p(x_n,x_m).$$

(3.9)

On the other hand, since the sequence $\{x_n\}$ is a Cauchy sequence in the metric space $(Y,d_p)$, we also have

$$\underset{n\to \mathrm{\infty }}{lim}{d}_p(x_n,x_m)=0.$$

Since $d_p(x,y)=2p(x,y)-p(x,x)-p(y,y)$, we can deduce that

$$\underset{n\to \mathrm{\infty }}{lim}p(x_n,x_m)=0.$$

(3.10)

Since $Y={\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of X with respect to f, the sequence $\{x_n\}$ has infinite terms in each $A_i$ for $i\in \{1,2,\dots ,m\}$. Now, for all $i=1,2,\dots ,m$, we may take a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ with $x_{n_k}\in A_{i-1}$ and also all converge to ν. Using (3.9) and (3.10), we have

$$p(\nu ,\nu )=\underset{n\to \mathrm{\infty }}{lim}p(x_n,\nu )=\underset{n\to \mathrm{\infty }}{lim}p(x_{n_k},\nu )=0.$$

By (3.1),

$$\begin{array}{rl}p(x_{n_{k+1}},f\nu )& =p(f{x}_{n_k},f\nu )\\ \le \varphi (p(x_{n_k},\nu ))-\psi (p(x_{n_k},\nu ))\\ \le \varphi (p(x_{n_k},\nu )).\end{array}$$

Letting $k\to \mathrm{\infty }$, we have

$$p(\nu ,f\nu )\le 0,$$

and so $\nu =f\nu$.

Step 4. Finally, to prove the uniqueness of the fixed point, let μ be another fixed point of f in ${\bigcap }_{i=1}^m{A}_i$. By the cyclic character of f, we have $\mu ,\nu \in {\bigcap }_{i=1}^n{A}_i$. Since f is a cyclic weaker $\mathcal{MK}$-contraction, we have

$$\begin{array}{rl}p(\nu ,\mu )& =p(\nu ,f\mu )\\ =\underset{n\to \mathrm{\infty }}{lim}p(x_{n_{k+1}},f\mu )\\ =\underset{n\to \mathrm{\infty }}{lim}p(f{x}_{n_k},f\mu )\\ \le \underset{n\to \mathrm{\infty }}{lim}[\varphi (p(x_{n_k},\mu ))-\psi (p(x_{n_k},\mu ))]\\ \le p(\nu ,\mu )-\psi (p(\nu ,\mu )),\end{array}$$

and we can conclude that

$$\psi (p(\nu ,\mu ))=0,$$

which implies $p(\nu ,\mu )=0$. So, we have $\mu =\nu$. We complete the proof.  □

The following provides an example for Theorem 4.

Example 2 Let $X=[0,1]$ and $A=[0,1]$, $B=[0,\frac{1}{2}]$, $C=[0,\frac{1}{4}]$. We define the partial metric p on X by

$$p(x,y)=max\{x,y\}\text{for all }x,y\in X,$$

and define the function $f:X\to X$ by

$$f(x)=\frac{x^2}{1+x}\text{for all }x\in X.$$

Now, we let $\psi ,\varphi :{\mathbb{R}}^{+}\to {\mathbb{R}}^{+}$ be

$$\varphi (t)=\frac{4t}{5}\text{and}\psi (t)=\frac{t}{5(1+t)}.$$

Then f is a cyclic $\mathcal{MK}$-contraction and 0 is the unique fixed point.

By Theorem 4, it is easy to get the following corollary.

Corollary 1 Let $(X,p)$ be a complete partial metric space, $m\in \mathbb{N}$, $A_1,A_2,\dots ,A_m$ be nonempty closed subsets of X, $Y={\bigcup }_{i=1}^m{A}_i$ and let $f:Y\to Y$. Assume that

• (1) ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of Y with respect to f;

• (2) for any $x\in A_i$, $y\in A_{i+1}$, $i=1,2,\dots ,m$,

  $$p(fx,fy)\le \varphi (p(x,y)),$$

where $A_{m+1}=A_1$ and $\varphi \in \mathrm{\Phi }$.

Then f has a unique fixed point $z\in {\bigcap }_{i=1}^m{A}_i$.