- Research
- Open access
- Published:
Common fuzzy fixed points for fuzzy mappings
Fixed Point Theory and Applications volume 2013, Article number: 14 (2013)
Abstract
Let be a metric space and S, T be mappings from X to a set of all fuzzy subsets of X. We obtained sufficient conditions for the existence of a common α-fuzzy fixed point of S and T.
1 Introduction
Fixed point theorems play a fundamental role in demonstrating the existence of solutions to a wide variety of problems arising in mathematics, physics, engineering, medicine and social sciences. The study of fixed point theorems in fuzzy mathematics was instigated by Weiss [1], Butnariu [2], Singh and Talwar [3], Estruch and Vidal [4], Wang et al. [5], Mihet [6], Qiu et al. [7] and Beg and Abbas [8]. Heilpern [9] introduced the concept of fuzzy contraction mappings and established the fuzzy Banach contraction principle on a complete metric linear spaces with the -metric for fuzzy sets. Azam and Beg [10] proved common fixed point theorems for a pair of fuzzy mappings satisfying Edelstein, Alber and Guerr-Delabriere type contractive conditions in a metric linear space. Azam et al. [11] presented some fixed point theorems for fuzzy mappings under Edelstein locally contractive conditions on a compact metric space with the -metric for fuzzy sets. Frigon and Regan [12] generalized the Heilpern theorem under a contractive condition for 1-level sets (i.e., ) of a fuzzy contraction T on a complete metric space, where 1-level sets are not assumed to be convex and compact. Amemiya and Takahashi [13] studied some mathematical properties of contractive type set-valued and fuzzy mappings to obtain fixed points of fuzzy mappings by using the concept of w-distance (see [13]) in complete metric spaces. Recently, Zhang et al. [14] proved some common fixed point theorems for contraction mappings in a new fuzzy metric space.
The aim of this paper is to obtain a common α-fuzzy fixed point of a pair of fuzzy mappings S and T on a complete metric space under a generalized contractive condition for α-level sets (i.e., , ) of S and T in connection with Hausdorff metric for fuzzy sets. Our result (Theorem 5) generalizes the results proved by Azam and Arshad [[15], Theorem 4], Bose and Sahani [16] and Vijayaraju and Marudai [[17], Theorem 3.1] among others.
2 Preliminaries
Let be a metric space and be the family of nonempty closed and bounded subsets of X. For , define
where
A fuzzy set in X is a function with domain X and values in . If A is a fuzzy set and , then the function-value is called the grade of membership of x in A. The α-level set of A is denoted by and is defined as follows:

Here, denotes the closure of the set B. Let be the collection of all fuzzy sets in a metric space X. For , means for each . We denote the fuzzy set by unless and until it is stated, where is the characteristic function of the crisp set A. If there exists an such that , then define

If for each , then define

We write instead of . A fuzzy set A in a metric linear space V is said to be an approximate quantity if and only if is compact and convex in V for each and
We denote the collection of all approximate quantities in a metric linear space X by . Let X be an arbitrary set, Y be a metric space. A mapping T is called a fuzzy mapping if T is a mapping from X into . A fuzzy mapping T is a fuzzy subset on with a membership function . The function is the grade of membership of y in .
Definition 1 Let S, T be fuzzy mappings from X into . A point z in X is called an α-fuzzy fixed point of T if . The point z is called a common α-fuzzy fixed point of S and T if . When , it is called a common fixed point of fuzzy maps.
For the sake of convenience, we first state some known results for subsequent use in the next section.
Lemma 2 [18]
Let be a metric space and , then for each ,
Lemma 3 [18]
Let be a metric space and , then for each , , there exists an element such that .
Lemma 4 [19]
Let V be a metric linear space, be a fuzzy mapping and . Then there exists such that .
3 Common fuzzy fixed points
In this section, we establish Theorem 5 on the existence of an α-fuzzy fixed point of a fuzzy mapping and also obtain a fixed point of fuzzy mappings (see Corollaries 8 and 9) and multivalued mappings (see Corollary 7).
Theorem 5 Let be a complete metric space and let S, T be fuzzy mappings from X to satisfying the following conditions:
-
(a)
for each , there exists such that
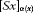 ,
, 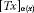 are nonempty closed bounded subsets of X and
are nonempty closed bounded subsets of X and -
(b)
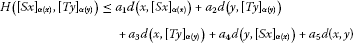 (1)
(1)
for all , where , , , , are nonnegative real numbers and and either or . Then there exists such that .
Proof We consider the following three possible cases:
-
(i)
;
-
(ii)
;
-
(iii)
, .
Case (i): For , there exists such that  is a nonempty closed bounded subset of X. Take
is a nonempty closed bounded subset of X. Take  and similarly
and similarly  . Then by Lemma 2, we obtain
. Then by Lemma 2, we obtain

Now, inequality (1) implies that

Using together with the fact that  , we obtain
, we obtain

It follows that  , which further implies that
, which further implies that

Again, inequality (1) gives  . It follows that
. It follows that

Case (ii): It can be easily seen that

Case (iii): Let
If , then and so . Moreover, if ,
Choose , then by hypotheses there exists such that is a nonempty closed bounded subset of X. For convenience, we denote by . Let ; for this , there exists such that is a nonempty closed bounded subset of X. Since , by Lemma 3, there exists such that
It implies that
By the same argument, we can find and such that
By induction, we produce a sequence of points of X,

such that

It implies that
Similarly,
It follows that for each ,
and
Then for , we have
Similarly, we obtain

and
Since , it follows from Cauchy’s root test , are convergent series. Therefore, is a Cauchy sequence. Since X is complete, there exists such that . Now,

It further implies that
Letting , we have . It implies that . Similarly, by using
we can show that , which implies that .
The proof of the following corollary illustrates a link between multivalued mappings and fuzzy mappings. It is well known [20] that
are isometric embeddings under and , respectively, where
and is a crisp set. □
In the following, we furnish an illustrative example to highlight the utility of Theorem 5.
Example 6 Let be crisp sets. Define as follows:
Define fuzzy mappings as follows:

and
Then, for ,
and
Now,
Since for each and X is not linear, therefore [[12], Theorems 2.1, 2.2] and main results in [9–11, 16] are not applicable to find . Now, for all and

It follows that for
 if . Hence, for , , the conditions of Theorem 5 are satisfied to obtain . Since , the results proved by Vijayaraju and Marudai [[17], Theorem 3.1] and Azam and Arshad [[15], Theorem 4] are also not applicable.
if . Hence, for , , the conditions of Theorem 5 are satisfied to obtain . Since , the results proved by Vijayaraju and Marudai [[17], Theorem 3.1] and Azam and Arshad [[15], Theorem 4] are also not applicable.
Corollary 7 Let be a complete metric space and be multivalued mappings. Suppose that for all ,
where , , , , are nonnegative real numbers and and either or . Then there exists such that .
Proof Consider a mapping and a pair of fuzzy mappings defined by

Then
Thus, Theorem 5 can be applied to obtain such that
□
Corollary 8 [16]
Let be a complete metric linear space and be fuzzy mappings, and for all ,
where , , , , are nonnegative real numbers and and either or . Then there exists such that , .
Proof Let , then by Lemma 4 there exists such that . Similarly, we can find such that . It follows that for each , , are nonempty closed bounded subsets of X. As , by the definition of a -metric for fuzzy sets, we have
for all . It implies that
for all . Since for each , therefore for each . It implies that , similarly, . This further implies that for all ,

Now, by Theorem 5, we obtain such that , i.e., , . □
In the following, we suppose that (for details, see [2, 21]) is the set-valued mapping induced by fuzzy mappings , i.e.,
Corollary 9 Let be a complete metric space and be fuzzy mappings such that for all , , nonempty closed bounded subsets of X and
for all , where , , , , are nonnegative real numbers and and either or . Then there exists a point such that and for all .
Proof By Corollary 7, there exists such that . Then by [[21], Lemma 1], we obtain
for all . □
Remark 10 The result proved by Vijayaraju and Marudai [[17], Theorem 3.1] and Azam and Arshad [[15], Theorem 4] is the case when and in Theorem 5. Corollary 9 also generalizes the results proved by Heilpern [9] and Frigon and Regan [[12], Theorems 2.1, 2.2] for

4 Conclusion
In this paper, we obtained fixed point results for fuzzy set-valued mappings under a generalized contractive condition related to the -metric which is useful for computing Hausdorff dimensions. These dimensions help us to understand -space which is used in high energy physics. Our results are also useful in geometric problems arising in high energy physics. This is because events in this case are mostly fuzzy sets.
References
Weiss MD: Fixed points and induced fuzzy topologies for fuzzy sets. J. Math. Anal. Appl. 1975, 50: 142–150. 10.1016/0022-247X(75)90044-X
Butnariu D: Fixed point for fuzzy mapping. Fuzzy Sets Syst. 1982, 7: 191–207. 10.1016/0165-0114(82)90049-5
Singh SL, Talwar R: Fixed points of fuzzy mappings. Soochow J. Math. 1993, 19(1):95–102.
Estruch, VD, Vidal, A: A note on fixed fuzzy points for fuzzy mappings. Proceedings of the II Italian-Spanish Congress on General Topology and Its Applications (Italian) (Trieste, 1999). Rend. Ist. Mat. Univ. Trieste 32(suppl. 2), 39–45 (2001)
Wang G, Wu C, Wu C: Fuzzy α -almost convex mappings and fuzzy fixed point theorems for fuzzy mappings. Ital. J. Pure Appl. Math. 2005, 17: 137–150.
Mihet D: On fuzzy ϵ -contractive mappings in fuzzy metric spaces. Fixed Point Theory Appl. 2007., 2007: Article ID 87471
Qiu D, Shu L, Guan J: Common fixed point theorems for fuzzy mappings under φ -contraction condition. Chaos Solitons Fractals 2009, 41(1):360–367. 10.1016/j.chaos.2008.01.003
Beg I, Abbas M: Invariant approximation for fuzzy nonexpansive mappings. Math. Bohem. 2011, 136(1):51–59.
Heilpern S: Fuzzy mappings and fixed point theorems. J. Math. Anal. Appl. 1981, 83: 566–569. 10.1016/0022-247X(81)90141-4
Azam A, Beg I: Common fixed points of fuzzy maps. Math. Comput. Model. 2009, 49: 1331–1336. 10.1016/j.mcm.2008.11.011
Azam A, Arshad M, Beg I: Fixed points of fuzzy contractive and fuzzy locally contractive maps. Chaos Solitons Fractals 2009, 42: 2836–2841. 10.1016/j.chaos.2009.04.026
Frigon M, O’Regan D: Fuzzy contractive maps and fuzzy fixed points. Fuzzy Sets Syst. 2002, 129: 39–45. 10.1016/S0165-0114(01)00171-3
Amemiya M, Takahashi W: Fixed point theorems for fuzzy mappings in complete metric spaces. Fuzzy Sets Syst. 2002, 125: 253–260. 10.1016/S0165-0114(01)00046-X
Zhang W, Qiu D, Li Z, Xiong G: Common fixed point theorems in a new fuzzy metric space. J. Appl. Math. 2012., 2012: Article ID 890678
Azam A, Arshad M: A note on ‘Fixed point theorems for fuzzy mappings’ by P. Vijayaraju and M. Marudai. Fuzzy Sets Syst. 2010, 161: 1145–1149. 10.1016/j.fss.2009.10.016
Bose RK, Sahani D: Fuzzy mappings and fixed point theorems. Fuzzy Sets Syst. 1987, 21: 53–58. 10.1016/0165-0114(87)90152-7
Vijayaraju P, Marudai M: Fixed point theorems for fuzzy mappings. Fuzzy Sets Syst. 2003, 135: 401–408. 10.1016/S0165-0114(02)00367-6
Nadler SB: Multivalued contraction mappings. Pac. J. Math. 1969, 30: 475–488. 10.2140/pjm.1969.30.475
Arora SC, Sharma V: Fixed points for fuzzy mappings. Fuzzy Sets Syst. 2000, 110: 127–130. 10.1016/S0165-0114(97)00366-7
Azam A, Arshad M, Vetro P: On a pair of fuzzy ϕ -contractive mappings. Math. Comput. Model. 2010, 52: 207–214. 10.1016/j.mcm.2010.02.010
Shi-sheng Z: Fixed point theorems for fuzzy mappings (II). Appl. Math. Mech. 1986, 7(2):147–152. 10.1007/BF01897057
Acknowledgements
Authors are grateful to the editor and referees for their valuable suggestions and critical remarks for improving this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
IB gave the idea and AA wrote the initial draft. Both authors read and agreed upon the draft and finalized the manuscript. Correspondence was mainly done by IB. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Azam, A., Beg, I. Common fuzzy fixed points for fuzzy mappings. Fixed Point Theory Appl 2013, 14 (2013). https://doi.org/10.1186/1687-1812-2013-14
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2013-14
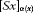 ,
, 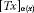 are nonempty closed bounded subsets of X and
are nonempty closed bounded subsets of X and