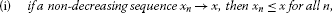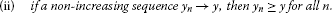- Research
- Open access
- Published:
Coupled coincidence point theorems for contractions in generalized fuzzy metric spaces
Fixed Point Theory and Applications volume 2012, Article number: 196 (2012)
Abstract
In this paper, we introduce the concept of a mixed g-monotone mapping and prove coupled coincidence and common coupled fixed point theorems for mappings under ϕ-contractive conditions in partially ordered generalized fuzzy metric spaces. We also give an example to illustrate the theorems.
MSC:47H10, 54H25.
1 Introduction
The theory of fuzzy sets has evolved in many directions after investigation of the notion of fuzzy sets by Zadeh [1]. Many authors have introduced the concept of a fuzzy metric space in different ways [2, 3]. George and Veeramani [4, 5] modified the concept of a fuzzy metric space introduced by Kramosil and Michalek [3] and defined a Hausdorff topology on this fuzzy metric space. They showed also that every metric induces a fuzzy metric. Later, many fixed point theorems in fuzzy metric spaces and probabilistic metric spaces have been obtained by [6–10].
Nieto and Lopez [11], Ran and Reurings [12], Petrusel and Rus [13] presented some new results for contractions in partially ordered metric spaces. The main idea in [11, 12] involves combining the ideas of the iterative technique in the contractive mapping principle with those in the monotone technique, discussing the existence of a solution to first-order ordinary differential equations with periodic boundary conditions and some applications to linear and nonlinear matrix equations.
Bhaskar and Lakshmikantham [14], Lakshmikantham and Ćirić [15] discussed coupled coincidence and coupled fixed point theorems for two mappings F and g, where F has the mixed g-monotone property and F and g commute. The results were used to study the existence of a unique solution to a periodic boundary value problem. In [16], Choudhury and Kundu established a similar result under the condition that F and g are compatible mappings and the function g is monotone increasing. For more details on ordered metric spaces, we refer to [17–19] and references mentioned therein.
Alternatively Mustafa and Sims [20] introduced a new notion of a generalized metric space called G-metric space. Mujahid Abbas et al. [23] proved a unique fixed point of four R-weakly commuting maps in G-metric spaces, and Mujahid Abbas et al. [24] obtained some common fixed point results of maps satisfying the generalized -weak commuting condition in partially ordered G-metric spaces. Rao et al. [22] proved two unique common coupled fixed-point theorems for three mappings in symmetric G-fuzzy metric spaces. Sun and Yang [21] introduced the concept of G-fuzzy metric spaces and proved two common fixed-point theorems for four mappings. Some interesting references on G-metric spaces are [22–25].
In this paper, we introduce the concept of a mixed g-monotone mapping, which is a generalization of the mixed monotone mapping, and prove coupled coincidence point and coupled common fixed point theorems for mappings under ϕ-contractive conditions in partially ordered G-fuzzy metric spaces. The work is an extension of the fixed point result in fuzzy metric spaces and the condition is different from [14–16] even in metric spaces. We also give an example to illustrate the theorems.
Recall that if is a partially ordered set and satisfies that for , implies , then a mapping F is said to be non-decreasing. Similarly, a non-increasing mapping is defined.
Before giving our main results, we recall some of the basic concepts and results in G-metric spaces and G-fuzzy metric spaces.
2 Preliminaries
Definition 2.1 [20]
Let X be a nonempty set, and let be a function satisfying the following properties:
(G-1) if ,
(G-2) for all with ,
(G-3) for all with ,
(G-4) , symmetry in all three variables,
(G-5) for all .
The function G is called a generalized metric or a G-metric on X and the pair is called a G-metric space.
Definition 2.2 [20]
The G-metric space is called symmetric if for all .
Definition 2.3 [20]
Let be a G-metric space, and let be a sequence in X. A point is said to be the limit of if and only if . In this case, the sequence is said to be G-convergent to x.
Definition 2.4 [20]
Let be a G-metric space, and let be a sequence in X. is called a G-Cauchy sequence if and only if . is called G-complete if every G-Cauchy sequence in is G-convergent in .
Proposition 2.1 [20]
In a G-metric space , the following are equivalent:
-
(i)
The sequence is G-Cauchy.
-
(ii)
For every , there exists such that for all .
Proposition 2.2 [20]
Let be a G-metric space; then the function is jointly continuous in all three of its variables.
Proposition 2.3 [20]
Let be a G-metric space; then for any , it follows that
-
(i)
if , then ,
-
(ii)
,
-
(iii)
,
-
(iv)
,
-
(v)
.
Let be a metric space. One can verify that is a G-metric space, where
or
If is a G-metric space, it easy to verify that is a metric space, where .
Definition 2.5 [26]
A binary operation is a continuous t-norm if ∗ satisfies the following conditions:
-
(i)
∗ is commutative and associative;
-
(ii)
∗ is continuous;
-
(iii)
for all ;
-
(iv)
whenever and for all .
Definition 2.6 [21]
A 3-tuple is said to be a G-fuzzy metric space (denoted by GF space) if X is an arbitrary nonempty set, ∗ is a continuous t-norm and G is a fuzzy set on satisfying the following conditions for each :
(GF-1) for all with ;
(GF-2) for all with ;
(GF-3) if and only if ;
(GF-4) , where p is a permutation function;
(GF-5) (the triangle inequality);
(GF-6) is continuous.
Remark 2.1 Let , , , in (GF-5), we have
which implies that
for all and .
A GF space is said to be symmetric if for all and for each .
Example 2.1 Let X be a nonempty set, and let G be a G-metric on X. Define the t-norm and for all and , . Then is a GF space.
Remark 2.2 If is a fuzzy metric space [4], then is a GF space, where
In fact, we only need to verify (GF-5). Since

we have

which implies that (GF-5) holds.
Remark 2.3 If is a symmetric GF space, let , then is a fuzzy metric space [4].
Let be a GF space. For , the open ball with center and radius is defined by
A subset is called an open set if for each , there exist and such that .
Definition 2.7 [21]
Let be a GF space, then
-
(1)
a sequence in X is said to be convergent to x (denoted by ) if
for all .
-
(2)
a sequence in X is said to be a Cauchy sequence if
that is, for any and for each , there exists such that
for .
-
(3)
A GF space is said to be complete if every Cauchy sequence in X is convergent.
Lemma 2.1 [21]
Let be a GF space. Then is non-decreasing with respect to t for all .
Lemma 2.2 [21]
Let be a GF space. Then G is a continuous function on .
In the rest of the paper, will denote a GF space with a continuous t-norm ∗ defined as for all , and we assume that
Define , where and each satisfies the following conditions:
(Φ-1) ϕ is strict increasing;
(Φ-2) ϕ is upper semi-continuous from the right;
(Φ-3) for all , where .
Let , , where , then .
It is easy to prove that if , then for all .
Using (P), one can prove the following lemma.
Lemma 2.3 Let be a GF space. If there exists such that if for all , then .
Lemma 2.4 Let be a GF space. If we define by
for all and , then we have:
-
(1)
for each , there exists such that
-
(2)
The sequence in X is convergent if and only if as for all .
Proof (1) For any , let and , and so, by the triangular inequality (GF-5) and Remark 2.1, for any , we have

which implies, by Definition 2.1 of , that
Since is arbitrary, we have
-
(2)
Since G is continuous in its fourth argument, by Definition 2.1 of , we have
This proved the lemma. □
Lemma 2.5 Let be a GF space and be a sequence in X. If there exists such that
for all and , then is a Cauchy sequence in X.
Proof Let be defined by (2.1). For each and , putting , we will prove that
Since ϕ is upper semi-continuous from right, for given and each , there exists such that . From the definition of by (2.1), it follows from that for all .
Thus, by (2.2), (2.3) and Lemma 2.1, we get

Again by Definition 2.1, we get
By the arbitrariness of ε, we have
So, we can infer that . If not, then by (2.4), we have , which is a contradiction. Hence, (2.4) implies that , and (2.3) is proved.
Again and again using (2.3), we get
By Lemma 2.4, for each , there exists such that
Since , by condition (Φ-3) we have . So, for given , there exists such that . Thus, it follows from (2.5) that
which implies that for all with . Therefore, is a Cauchy sequence in X. □
3 Main results
Definition 3.1 [14]
Let be a partially ordered set. The mapping F is said to have the mixed monotone property if F is monotone non-decreasing in its first argument and is monotone non-increasing in its second argument; that is, for any ,
and
Definition 3.2 [14]
An element is called a coupled fixed point of the mapping if
Definition 3.3 [15]
Let be a partially ordered set and and . We say F has the mixed g-monotone property if F is monotone g-non-decreasing in its first argument and is monotone g-non-increasing in its second argument; that is, for any ,

and

Note that if g is the identity mapping, then Definition 3.3 reduces to Definition 3.1.
Example 3.1 Let with the natural ordering of real numbers. Let and be defined as
Then F is not mixed monotone but mixed g-monotone.
Definition 3.4 [15]
Let X be a nonempty set, and , then
-
(1)
An element is called a coupled coincidence point of the mappings F and g if
-
(2)
An element is called a common coupled fixed point of the mappings F and g if
Definition 3.5 The mappings and are said to be compatible if
and
for all whenever and are sequences in X such that
for all are satisfied.
Definition 3.6 [16]
The mappings and are called w-compatible if
whenever and for some .
Remark 3.1 It is easy to prove that if F and g are compatible then they are w-compatible.
Theorem 3.1 Let be a partially ordered set and be a complete GF space. Let and be two mappings such that F has the mixed g-monotone property and there exists such that

for all , for which and , or and .
Suppose , g is continuous and F and g are compatible. Also suppose
-
(a)
F is continuous or
-
(b)
X has the following properties:
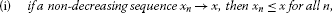 (3.6)
(3.6)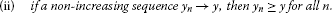 (3.7)
(3.7)
If there exists such that and , then there exist such that and ; that is, F and g have a coupled coincidence point in X.
Proof Let be such that and . Since , we can choose such that and . Continuing in this way, we construct two sequences and in X such that
We shall show that


for all .
We shall use the mathematical induction. Let . Since and , and as and , we have and . Thus, (3.9) and (3.10) hold for . Suppose now that (3.9) and (3.10) hold for some fixed . Then since and , and as F has the mixed g-monotone property, from (3.8) and (3.3),
and from (3.8) and (3.4),
Now from (3.11) and (3.12), we get and . Thus, by mathematical induction, we conclude that (3.9) and (3.10) hold for all . Therefore,
and
By putting (, , , ) in (3.5), we get

So, by (3.8), we have

Now, by Lemma 2.5, is a Cauchy sequence.
By putting (, , , ) in (3.5), we get

So, by (3.8), we have

Now, by Lemma 2.5, is also a Cauchy sequence.
Since X is complete, there exist such that
Since F and g are compatible, we have by (3.15)
and
for all . Next, we prove that and .
Let (a) hold. Since F and g are continuous, by Lemma 2.2, taking limits as in (3.16) and (3.17), we get
for all . We have , .
Next, we suppose that (b) holds. By (3.9), (3.10), (3.15), we have for all
Since F and g are compatible and g is continuous, by (3.16) and (3.17), we have
and
Now, we have
for all . Taking the limit as in the above inequality, by continuity of G, using (3.8) and (3.19), we have

By (3.5), (3.19) and the above inequality, we have that

Letting , which implies that by Lemma 2.3, and similarly, by the virtue of (3.8), (3.15) and (3.20), we get . Thus, we have proved that F and g have a coupled coincidence point in X.
This completes the proof of Theorem 3.1. □
Taking (the identity mapping) in Theorem 3.1, we get the following consequence.
Corollary 3.1 Let be a partially ordered set and be a complete GF space. Let be a mapping such that F has the mixed monotone property and there exists such that
for all , for which and . Suppose
-
(a)
F is continuous or
-
(b)
X has the following properties:
-
(i)
if a non-decreasing sequence , then for all n,
-
(ii)
if a non-increasing sequence , then for all n.
If there exists such that and , then there exist such that and ; that is, F has a coupled fixed point in X.
Now, we shall prove the existence and uniqueness theorem of a coupled common fixed point. Note that if is a partially ordered set, then we endow the product with the following partial order:
Theorem 3.2 In addition to the hypotheses of Theorem 3.1, suppose that for every , there exists a satisfying or such that is comparable to , . Then F and g have a unique common coupled fixed point; that is, there exists a unique such that
Proof From Theorem 3.1, the set of coupled coincidence points is nonempty. We shall show that if and are coupled coincidence points, that is, if , and , , then
By assumption, there is such that is comparable with , . Put , and choose so that and . Then, similarly as in the proof of Theorem 3.1, we can inductively define sequences and such that
With the similar proof as in Theorem 3.1, we can prove that the limits of and exist.
Since and are comparable, it is easy to show that and are comparable for all . Thus, from (3.5),

for each . Letting , we get
Similarly, one can prove that
By (3.22) and (3.23), we have
which shows that .
Similarly, one can prove that . Thus, we proved (3.21).
Since and , by the compatibility of F and g, we can get the w-compatibility of F and g, which implies
and
Denote , . Then from (3.24) and (3.25),
Thus, is a coupled coincidence point. From (3.21) with , , it also follows , , that is,
From (3.26) and (3.27), we get
Therefore, is a common coupled fixed point of F and g. To prove the uniqueness, assume that is another coupled common fixed point. Then by (3.21) we have and . □
From Remark 2.3, let be a symmetric GF space. From Theorem 3.1, we get the following
Corollary 3.2 Let be a partially ordered set and be a complete fuzzy metric space. Let and be two mappings such that F has the mixed g-monotone property and there exists such that
for all , , for which and , or and .
Suppose , g is continuous and F and g are compatible. Also suppose
-
(a)
F is continuous or
-
(b)
X has the following properties:
-
(i)
if a non-decreasing sequence , then for all n,
-
(ii)
if a non-increasing sequence , then for all n.
If there exist such that and , then there exist such that and , that is, F and g have a coupled coincidence point in X.
Remark 3.2 Compared with the results in [15, 16], we can find that Theorem 3.1 is different in the following aspects:
-
(1)
We assume that F and g are compatible, which is weaker than the conditions in [15, 16], where Theorem 2.1 in [15] assumes commutation for F and g, and Theorem 3.1 in [16] requires g to be a monotone function.
(2) We have a different contractive condition from [15, 16] even in a metric space.
-
(3)
In our paper, we assume that , which is a stronger condition than that in [15, 16]. But we would like to point out that in the case of , where , the two conditions are equivalent.
Next, we give an example to demonstrate Theorem 3.1.
Example 3.2 Let , . Then is a partially ordered set with the natural ordering of real numbers. Let
for all . Then is a complete GF space.
Let and be defined as

F obeys the mixed g-monotone property.
Let for . Let and be two sequences in X such that
then , . Now, for all ,

and
Then it follows that

Hence, the mappings F and g are compatible in X. Also, and are two points in X such that
and
We next verify the inequality of Theorem 3.1. We take such that and , that is, , .
We consider the following cases:
Case 1: and , then
Case 2: , . Since , then cannot happen.
Case 3: and , then
Case 4: and with and , then and , that is, . Obviously, (3.5) is satisfied.
Thus, it is verified that the functions F, g, ϕ satisfy all the conditions of Theorem 3.1. Here is the coupled coincidence point of F and g in X, which is also their common coupled fixed point.
References
Zadeh LA: Fuzzy sets. Inf. Control 1965, 8: 338–353. 10.1016/S0019-9958(65)90241-X
Grabiec M: Fixed points in fuzzy metric spaces. Fuzzy Sets Syst. 1988, 27: 385–389. 10.1016/0165-0114(88)90064-4
Kramosil O, Michalek J: Fuzzy metric and statistical metric spaces. Kybernetica 1975, 11: 326–334.
George A, Veeramani P: On some results in fuzzy metric spaces. Fuzzy Sets Syst. 1994, 64: 395–399. 10.1016/0165-0114(94)90162-7
George A, Veeramani P: On some results of analysis for fuzzy metric spaces. Fuzzy Sets Syst. 1997, 90: 365–368. 10.1016/S0165-0114(96)00207-2
Sedghi S, Altun I, Shobe N: Coupled fixed point theorems for contractions in fuzzy metric spaces. Nonlinear Anal. TMA 2010, 72: 1298–1304. 10.1016/j.na.2009.08.018
Hu X: Common fixed point theorems for contractive mappings in fuzzy metric spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 363716
Ćirić L, Abbas M, Damjanovic B, Saadati R: Common fuzzy fixed point theorems in ordered metric spaces. Math. Comput. Model. 2011, 53: 1737–1741. 10.1016/j.mcm.2010.12.050
O’Regan D, Saadati R: Nonlinear contraction theorems in probabilistic spaces. Appl. Math. Comput. 2008, 195: 86–93. 10.1016/j.amc.2007.04.070
Hu X, Ma X: Coupled coincidence point theorems under contractive conditions in partially ordered probabilistic metric spaces. Nonlinear Anal. TMA 2011, 74: 6451–6458. 10.1016/j.na.2011.06.028
Nieto JJ, Lopez RR: Existence and uniqueness of fixed point in partially ordered sets and applications to ordinary differential equations. Acta Math. Sin. Engl. Ser. 2007, 23: 2205–2212. 10.1007/s10114-005-0769-0
Ran ACM, Reurings MCB: A fixed point theorem in partially ordered sets and some applications to matrix equations. Proc. Am. Math. Soc. 2004, 132: 1435–1443. 10.1090/S0002-9939-03-07220-4
Petrusel A, Rus IA: Fixed point theorems in ordered L-spaces. Proc. Am. Math. Soc. 2006, 134: 411–418.
Bhaskar TG, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal. TMA 2006, 65: 1379–1393. 10.1016/j.na.2005.10.017
Lakshmikantham V, Ćirić LB: Coupled fixed point theorems for nonlinear contractions in partially ordered metric space. Nonlinear Anal. 2009, 70: 4341–4349. 10.1016/j.na.2008.09.020
Choudhury BS, Kundu A: A coupled coincidence point result in partially ordered metric spaces for compatible mappings. Nonlinear Anal. 2010, 73: 2524–2531. 10.1016/j.na.2010.06.025
Agarwal RP, El-Gebeily MA, O’Regan D: Generalized contractions in partially ordered metric spaces. Appl. Anal. 2008, 87: 1–8. 10.1080/00036810701714164
Ćirić LB, Miheţ D, Saadati R: Monotone generalized contractions in partially ordered probabilistic metric spaces. Topol. Appl. 2009, 156: 2838–2844. 10.1016/j.topol.2009.08.029
Shakeri S, Ćirić L, Saadati R: Common fixed point theorem in partially ordered L-fuzzy metric spaces. Fixed Point Theory Appl. 2010., 2010: Article ID 125082. doi:10.1155/2010/125082
Mustafa Z, Sims B: A new approach to generalized metric spaces. J. Nonlinear Convex Anal. 2006, 7: 289–297.
Sun G, Yang K: Generalized fuzzy metric spaces with properties. Res. J. Appl. Sci. 2010, 2: 673–678.
Rao KPR, Altun I, Hima Bindu S: Common coupled fixed-point theorems in generalized fuzzy metric spaces. Adv. Fuzzy Syst. 2011., 2011: Article ID 986748. doi:10.1155/2011/986748
Abbas M, Khan S, Nazir T: Common fixed points of R -weakly commuting maps in generalized metric space. Fixed Point Theory Appl. 2011., 2011: Article ID 41
Abbas M, Nazir T, Radenović S: Common fixed point for generalized weakly contractive maps in partially ordered G -metric spaces. Appl. Math. Comput. 2012, 218: 9383–9395. http://dx.doi.org/10.1016/j.amc.2012.03.022 10.1016/j.amc.2012.03.022
Luong NV, Thuan NX: Coupled fixed point theorems in partially ordered G -metric spaces. Math. Comput. Model. 2012, 55: 1601–1609. 10.1016/j.mcm.2011.10.058
Schweizer B, Sklar A: Statistical metric spaces. Pac. J. Math. 1960, 10: 314–334.
Acknowledgements
The authors thank the referees for useful comments and suggestions for the improvement of the paper. This work was supported by the National Natural Science Foundation of China (71171150).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
All authors contributed equally and significantly in writing this paper. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hu, XQ., Luo, Q. Coupled coincidence point theorems for contractions in generalized fuzzy metric spaces. Fixed Point Theory Appl 2012, 196 (2012). https://doi.org/10.1186/1687-1812-2012-196
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2012-196