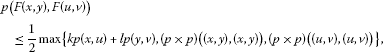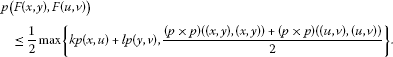- Research
- Open access
- Published:
Coupled fixed point theorems for partially contractive mappings
Fixed Point Theory and Applications volume 2012, Article number: 148 (2012)
Abstract
Recently, some authors have started to generalize fixed point theorems for contractive mappings in a class of generalized metric spaces in which the self-distance need not be zero. These spaces, partial metric spaces, were first introduced by Matthews in 1994. The proved fixed point theorems have been obtained for mappings satisfying contraction type conditions empty of the self-distance. In this article, we prove some coupled fixed point theorems for mappings satisfying contractive conditions allowing the appearance of self-distance terms. These partially contractive mappings do reflect the structure of the partial metric space, and hence their coupled fixed theorems generalize the previously obtained by (Aydi in Int. J. Math. Sci. 2011:Article ID 647091, 2011). Some examples are given to support our claims.
MSC:47H10, 54H25.
1 Introduction and preliminaries
The Banach contraction mapping principle is considered to be the soul of many extended fixed point theorems. It has widespread applications in many branches of mathematics, engineering and computer science. During the last decades many authors were able to generalize this principle [1–4]. After the appearance of partial metric spaces as a place for distinct research work into flow analysis, non-symmetric topology and domain theory [5, 6], many authors started to generalize this principle to these spaces (see [7–16]. However, the contraction type conditions used in those generalizations do not reflect the structure of a partial metric space apparently. Later, the authors in [17] proved a more reasonable contraction principle in the partial metric space in which they used self-distance terms. On the other hand, the theory of coupled fixed point theorems has recently attracted some authors (see [18–20]). Also, Meir-Keeler type common and tripled fixed point theorems have been recently considered over partial metric spaces [21, 22]. In this article, we prove a coupled partial contraction principle generalizing the recently published coupled fixed point theorems in [18]. An example is presented to show that our coupled partial contraction principle is worthy of investigation.
A partial metric space (PMS) (see, e.g., [5, 6]) is a pair (where denotes the set of all nonnegative real numbers) such that
(P1) (symmetry)
(P2) If then (equality)
(P3) (small self-distances)
(P4) (triangularity)
for all .
For a partial metric p on X, the function given by
is a (usual) metric on X. Each partial metric p on X generates a topology on X with a base of the family of open p-balls , where for all and .
Definition 1 (see, e.g., [5, 6, 13])
-
(i)
A sequence in a PMS converges to if and only if ;
-
(ii)
A sequence in a PMS is called Cauchy if and only if exists (and is finite);
-
(iii)
A PMS is said to be complete if every Cauchy sequence in X converges, with respect to , to a point such that ;
-
(iv)
A mapping is said to be continuous at , if for every , there exists such that .
Lemma 2 (see, e.g., [5, 6, 13])
-
(A)
A sequence is Cauchy in a PMS if and only if is Cauchy in a metric space ;
-
(B)
A PMS is complete if and only if the metric space is complete. Moreover,
(2)
A sequence is called 0-Cauchy [17] if . The partial metric space is called 0-complete [17, 23] if every 0-Cauchy sequence in x converges to a point with respect to p and . Clearly, every complete partial metric space is 0-complete. The converse need not be true.
Example 3 (see [17])
Let with the partial metric . Then is a 0-complete partial metric space which is not complete.
Let and define .
The following theorem was presented in [17].
Theorem 4 Let be a complete metric space, and a given mapping. Suppose that for each the following condition holds:
Then
-
(1)
the set is nonempty;
-
(2)
there is a unique such that ;
-
(3)
for each the sequence converges to u with respect to the metric .
If is a partial metric space, then clearly defined by is a partial metric, and hence is a partial metric space. Clearly, if is complete (0-complete) then so is . The minimum self partial distance in is defined by
The set of all points in with self partial distance is denoted by
Example 5 Let and provide X with the partial metric if both and otherwise. Then clearly is a complete partial metric space, and .
Definition 6 Let be a partial metric space and be a mapping. Then F is called
-
(a)
partially contractive if there exist constants such that for all ,
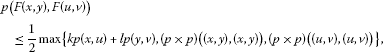 (3)
(3) -
(b)
strong partially contractive if there exist constants such that for all ,
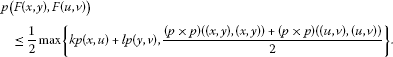 (4)
(4)
Aydi [18] proved the following coupled fixed point theorems in partial metric spaces:
Theorem 7 Let be a complete partial metric space. Suppose that the mapping satisfies the following contractive condition for all :
where with . Then F has a unique coupled fixed point. That is, there exists unique such that and .
Theorem 8 Let be a complete partial metric space. Suppose that the mapping satisfies the following contractive condition for all :
where with . Then F has a unique coupled fixed point.
2 Main results
Theorem 9 Let be a complete partial metric space and be a partially contractive mapping. Then
-
(a)
,
-
(b)
there exists a unique such that
(5) -
(c)
for each the sequence defined by
converges to with respect to . That is
Proof If , define the sequence by
We divide the proof of the claim (a) into the following steps:
Step I: The sequence is non-increasing. From the condition (3) we have
where . As a result of Step I, there exists such that
Step II: For each , we show that

where . We follow by induction. For , it is clear. Assume (6) is true for , and let us prove (6) for . Then by the help of (3), the triangle inequality and Step I, we have
where .
Step III: We show that
Let . Choose such that and . Then for , we have
where . On the other hand, (P3) implies and so (7) is obtained.
As a result of (7) and completeness of , there exists such that
Step IV: We show that for each the following holds:
First, note that by (P3) applied to p or , we have
By the help of the triangle inequality applied to p or , for each , we have
where . By the condition (3) and definition of , we have
where . Without loss of generality (by passing to subsequence if necessary), we may assume that for each , we have one of the following:
or
or
Substituting each of these cases in (12), letting and using (9) together with (11), we arrive at (10).
Step V: We prove that .
For each , pick with
We show that
Given put . If then by (3) we have
Hence, we conclude that for all ,
and
Now, if , then by the triangle inequality applied to , Step IV and (3), we have

Hence, using (16) and (17), we obtain
This shows (14) and so is Cauchy in the complete partial metric space . Therefore, there exists such that

In particular and so .
Now, let be arbitrary. Then by (9), (P3) applied to and (10), we have
Therefore, (P2) applied to implies that
and so is a coupled fixed point of F. Clearly, (9) implies that converges to the coupled fixed point with respect to which proves (c). To complete the proof of (b), assume and are both coupled fixed points of F. Then by (3) we have
From which it follows either and so implies that , or , and hence (P2) applied to implies . □
Remark 10 Although Theorem 9 does not imply the uniqueness of the fixed point, it is easy to see that, under the assumptions made, if and are both coupled fixed points for F satisfying , then . If the partially contractive condition (3) is replaced by the somewhat stronger condition below, the uniqueness of the coupled fixed point is guaranteed.
Theorem 11 Let be a complete partial metric space, and be a strong partially contractive mapping. Then there exists a unique coupled fixed point . Furthermore, and for each , the sequence defined by
converges to with respect to . That is
Proof By Theorem 9, we only need to prove the uniqueness of the coupled fixed point. If and are two coupled fixed points, then
where and . From (23) we distinguish the following cases:
Case 1: If , then and so .
Case 2: If , then and so . □
As a corollary, we obtain the already mentioned result [18] stated in Theorem 7. As well, let us remark that the result of Aydi in Theorem 7 is valid also for 0-complete partial metric spaces.
Corollary 12 Let be a 0-complete partial metric space. Suppose that the mapping satisfies the following contractive condition for all :
where with . Then F has a unique coupled fixed point such that . Also for each the sequence converges to with respect to the metric .
Proof The condition (24) implies that , which, in turn, by (9) implies . But then by (10) we have so the -limit of the sequence is actually the unique coupled fixed point . □
Example 13 Define by . Then is a complete partial metric space. Let be defined by
Then we have
-
(a)
There are no with such that , for all . That is, F does not verify the assumptions of Theorem 7. Indeed, if we assume that there exist with such that for all , we have
then
and
then we have , which is a contradiction.
-
(b)
There are no with such that . That is, F does not verify the assumptions of Theorem 8. Indeed, if we assume that there exist with such that for all , we have
(27)
Then we conclude that
which is a contradiction.
-
(c)
F is partially contractive. That is F verifies the assumptions of Theorem 9. Hence, it has the coupled fixed point . The condition (3) is clearly satisfied since for all .
-
(d)
Note that and hence the coupled Picard sequence converges for and for may converge or not depending on the particular choice of .
-
(e)
If F is replaced by , then it is strong partially contractive, and hence by Theorem 11, we guarantee the uniqueness of the coupled fixed point .
References
Khan MS, Sweleh M, Sessa S: Fixed point theorems by alternating distance between the points. Bull. Aust. Math. Soc. 1984, 30(1):1–9. 10.1017/S0004972700001659
Rhoades BE: Some theorems on weakly contractive maps. Nonlinear Anal., Theory Methods Appl. 2001, 47(4):2283–2693. 10.1016/S0362-546X(01)00352-2
Dutta PN, Choudhury BS: A generalization of contraction principle in metric spaces. Fixed Point Theory Appl. 2008., 2008: Article ID 406368
Boyd DW, Wong SW: On nonlinear contractions. Proc. Am. Math. Soc. 1969, 20: 458–464. 10.1090/S0002-9939-1969-0239559-9
Matthews, SG: Partial metric topology. Research report 212, Department of Computer Science, University of Warwick (1992)
Matthews SG: Partial metric topology. Annals of the New York Academy of Sciences 728. General Topology and Its Applications 1994, 183–197.
Abdeljawad T, Karapinar E, Taş K: Existence and uniqueness of a common fixed point on partial metric spaces. Appl. Math. Lett. 2011, 24(11):1900–1904. 10.1016/j.aml.2011.05.014
Abdeljawad T, Karapinar E, Taş K: A generalized contraction principle with control functions on partial metric spaces. Comput. Math. Appl. 2012, 6(3):716–719.
Abdeljawad T: Fixed points for generalized weakly contractive mappings in partial metric spaces. Math. Comput. Model. 2011, 54(11–12):2923–2927. 10.1016/j.mcm.2011.07.013
Oltra S, Valero O: Banach’s fixed point theorem for partial metric spaces. Rend. Ist. Mat. Univ. Trieste 2004, 36(1–2):17–26.
Valero O: On Banach fixed point theorems for partial metric spaces. Appl. Gen. Topol. 2005, 6(2):229–240.
Altun I, Sola F, Simsek H: Generalized contractions on partial metric spaces. Topol. Appl. 2010, 157(18):2778–2785. 10.1016/j.topol.2010.08.017
Altun I, Erduran A: Fixed point theorems for monotone mappings on partial metric spaces. Fixed Point Theory Appl. 2011., 2011: Article ID 508730. doi:10.1155/2011/508730
Shatanawi W, Samet B, Abbas M: Coupled fixed point theorems for mixed monotone mappings in ordered partial metric spaces. Math. Comput. Model. 2012, 55(3–4):680–687. doi:10.1016/j.mcm.2011.08.042 10.1016/j.mcm.2011.08.042
Aydi H, Karapinar E, Shatanawi W:Coupled fixed point results for -weakly contractive condition in ordered partial metric spaces. Comput. Math. Appl. 2011, 62: 4449–4460. 10.1016/j.camwa.2011.10.021
Shatanawi W, Nashine HK: A generalization of Banach’s contraction principle for nonlinear contraction in a partial metric space. J. Nonlinear Sci. Appl. 2012, 5: 37–43.
Ilić D, Pavlović V, Rakoc̆ević V: Some new extensions of Banach’s contraction principle to partial metric spaces. Appl. Math. Lett. 2011, 24: 1326–1330. 10.1016/j.aml.2011.02.025
Aydi H: Some coupled fixed point results on partial metric spaces. Int. J. Math. Sci. 2011., 2011: Article ID 647091
Berinde V: Coupled coincidence point theorems for mixed monotone nonlinear operators. Comput. Math. Appl. 2012. doi:10.1016/j.camwa.2012.02.12
Berinde V: Coupled fixed point theorems for ϕ -contractive mixed monotone mappings in partially ordered metric spaces. Nonlinear Anal. 2012, 65: 1379–1393.
Aydi H, Karapınar E: A Meir-Keeler common type fixed point theorem on partial metric spaces. Fixed Point Theory Appl. 2012., 2012: Article ID 26
Aydi H, Karapınar E: New Meir-Keeler type tripled fixed point theorems on ordered partial metric spaces. Math. Probl. Eng. 2012., 2012: Article ID 409872
Romaguera S: A Kirk type characterization of completeness for partial metric spaces. Fixed Point Theory Appl. 2010., 2010: Article ID 493298
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The author declares that they have no competing interests.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Abdeljawad, T. Coupled fixed point theorems for partially contractive mappings. Fixed Point Theory Appl 2012, 148 (2012). https://doi.org/10.1186/1687-1812-2012-148
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2012-148