A fixed point theorem for cyclic generalized contractions in metric spaces

Abstract

In this paper, we extend a recent result of V. Pata (J. Fixed Point Theory Appl. 10:299-305, 2011) in the frame of a cyclic representation of a complete metric space.

1 Introduction

One of the fundamental result in fixed point theory is the Banach contraction principle. It has various non-trivial applications in many branches of pure and applied sciences (see, for instance, [2, 7, 14] and references cited therein).

Let $(X,d)$ be a metric space and $f:X\to X$ be an operator. We say that f is a contraction if there exists $\lambda \in [0,1)$ such that, for all $x,y\in X$,

$$d(f(x),f(y))\le \lambda d(x,y).$$

(1.1)

In terms of Picard operator theory (see [13]), Banach contraction principle asserts that if f is a contraction and $(X,d)$ is complete, then f is a Picard operator. This result has been extended to other important classes of maps. Recently, Pata [8] proved that if $(X,d)$ is a complete metric space and $f:X\to X$ is an operator such that there exists fixed constants $\gamma \ge 0$, $\alpha \ge 1$ and $\beta \in [0,\alpha ]$ such that, for every $\epsilon \in [0,1]$ and every $x,y\in X$,

$$d(f(x),f(y))\le (1-\epsilon )d(x,y)+\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+\parallel x\parallel +\parallel y\parallel ]}^{\beta }$$

(1.2)

(where $\psi :[0,1]\to [0,\mathrm{\infty })$ is an increasing function vanishing with continuity at zero and $\parallel x\parallel :=d(x,x_0)$, with arbitrary $x_0\in X$), then f has a unique fixed point in X.

Remark 1.1 (see [8])

The condition (1.2) is weaker than the contraction condition (1.1). In fact, if

$$d(f(x),f(y))\le \lambda d(x,y),\text{for every }x,y\in X\text{ and some }\lambda \in [0,1),$$

then it can be verified that, for every $x,y\in X$, we have

$$d(f(x),f(y))\le (1-\epsilon )d(x,y)+\gamma {\epsilon }^{1+\theta }[1+\parallel x\parallel +\parallel y\parallel ],\text{for every }\theta >0,$$

where

$$\gamma =\gamma (\theta ,\lambda )=\frac{{\theta }^{\theta }}{{(1+\theta )}^{1+\theta }}\frac{1}{{(1-\lambda )}^{\theta }}.$$

Remark 1.2 (see [8])

The function $f:[1,\mathrm{\infty })\to [1,\mathrm{\infty })$ defined as

$$f(x)=-2+x-2\sqrt{x}+4\sqrt[4]{x}$$

has a unique fixed point $x^{\ast }=1$, but fails to be a contraction on any neighborhood both of 1 and of ∞.

Kirk, Srinivasan and Veeramani [6] obtained an extension of Banach’s fixed point theorem for mappings satisfying cyclical contractive conditions. Some generalizations of the results given in [6], using the setting of so-called fixed point structures, are presented in I. A. Rus [12]. In [10], Păcurar and Rus established a fixed point theorem for cyclic φ-contractions and they further discussed fixed point theory in metric spaces. In [3], Karapinar proved a fixed point theorem for cyclic weak φ-contraction mappings. Some other recent results concerning this topic are given in [1, 4, 5, 9, 11].

In the present paper, we obtain a fixed point theorem for a generalized contraction in the sense of the assumption (1.2), defined on a cyclic representation of a complete metric space.

2 Main results

We need first to recall a known concept.

Definition 2.1 ([3])

Let X be a nonempty set, m be a positive integer and $f:X\to X$ an operator. Then, we say that ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of X with respect to f if:

• (i) $X={\bigcup }_{i=1}^m{A}_i$, where $A_i$ are nonempty sets for each $i\in \{1,\dots ,m\}$;

• (ii) $f(A_1)\subset A_2,\dots ,f(A_{m-1})\subset A_m,f(A_m)\subset A_1$.

Let $(X,d)$ be a complete metric space. Selecting an arbitrary $x_1\in X$, we denote

$$\parallel x\parallel :=d(x,x_1),\text{for all }x\in X.$$

Our main result is as follows.

Theorem 2.2 Let $(X,d)$ be a complete metric space, m be a positive integer, $A_1,\dots ,A_m$ be closed nonempty subsets of X, $Y:={\bigcup }_{i=1}^m{A}_i$, $\psi :[0,1]\to [0,\mathrm{\infty })$ be an increasing function vanishing with continuity at zero, and $f:Y\to Y$ be an operator. Assume that:

• 1. ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of Y with respect to f;

• 2. For every $\epsilon \in [0,1]$, $x\in A_i$, and $y\in A_{i+1}$ ($i\in \{1,\dots ,m\}$, where $A_{m+1}=A_1$), we have

  $$d(f(x),f(y))\le (1-\epsilon )d(x,y)+\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+\parallel x\parallel +\parallel y\parallel ]}^{\beta },$$

  (2.1)

where $\gamma \ge 0$, $\alpha \ge 1$ and $\beta \in [0,\alpha ]$ are fixed constants.

Then, we have the following conclusions:

• (i) f is a Picard operator, i.e., f has a unique fixed point $x^{\ast }\in {\bigcap }_{i=1}^m{A}_i$ and the Picard iteration sequence ${\{f^n(x)\}}_{n\in \mathbb{N}}$ converges to $x^{\ast }$, for any initial point $x\in Y$;

• (ii) the following estimates hold:

  $$\begin{array}{c}d(x_n,x^{\ast })\le \parallel x^{\ast }\parallel ,n\ge 2;\hfill \\ d(x_n,x_1)\le 2\parallel x^{\ast }\parallel ,n\ge 2.\hfill \end{array}$$

Proof (i) For convenience of notation, if $j>m$, define $A_j=A_i$ where $i=jmodm$ and $1\le i\le m$. Let $x_1\in A_1$. Starting from $x_1$, let ${\{x_n\}}_{n\ge 1}$ be the Picard iteration defined by the sequence

$$x_n=f(x_{n-1})=f^{n-1}(x_1),n\ge 2,$$

and set $c_n=\parallel x_n\parallel$. Assume $x_n\ne x_{n+1}$ for all n. By (2.1), we have

$$d(x_n,x_{n+1})\le d(x_{n-1},x_n)\le \cdots \le d(x_1,x_2)=c_2.$$

(2.2)

First, we prove that the sequence ${(c_n)}_{n\in {\mathbb{N}}^{\ast }}$ is bounded. By (2.2) we get that

$$\begin{array}{rcl}{c}_n& \le & d(x_n,x_{n+1})+d(x_{n+1},x_2)+d(x_2,x_1)\le d(x_{n+1},x_2)+2c_2\\ =& d(f(x_n),f(x_1))+2c_2.\end{array}$$

Since $x_1\in A_1$ and $x_n\in A_n$, from (2.1), we obtain that

$$\begin{array}{rcl}{c}_n& \le & (1-\epsilon )d(x_n,x_1)+\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+\parallel x_n\parallel +\parallel x_1\parallel ]}^{\beta }+2c_2\\ =& (1-\epsilon )c_n+\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+c_n]}^{\beta }+2c_2\\ \le & (1-\epsilon )c_n+a{\epsilon }^{\alpha }\psi (\epsilon )c_n^{\alpha }+b,\end{array}$$

where $c_1=\parallel x_1\parallel =d(x_1,x_1)=0$, $\beta \le \alpha$, and for some $a,b>0$. Thus,

$$\epsilon c_n\le a{\epsilon }^{\alpha }\psi (\epsilon )c_n^{\alpha }+b.$$

If there is a subsequence ${(c_{n_k})}_{k\in {\mathbb{N}}^{\ast }}\to \mathrm{\infty }$, the choice $\epsilon ={\epsilon }_k=\frac{(1+b)}{c_{n_k}}$ leads to the contradiction

$$1\le a{(1+b)}^{\alpha }\psi ({\epsilon }_k)\to 0.$$

Therefore, the sequence $(c_n)$ is bounded.

From (2.2) we obtain that the sequence $\{d(x_n,x_{n+1})\}$ is nonincreasing and then it is convergent to the real number

$$\underset{n\to \mathrm{\infty }}{lim}d(x_n,x_{n+1})=r=inf\{d(x_{n-1},x_n):n=2,3,\dots \}.$$

Now we show that $r=0$. Assume that $r>0$. Let $x_n\in A_n$ and $x_{n+1}\in A_{n+1}$. By (2.1), we have

$$\begin{array}{rcl}r& \le & d(x_n,x_{n+1})=d(f(x_{n-1}),f(x_n))\\ \le & (1-\epsilon )d(x_{n-1},x_n)+\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+\parallel x_{n-1}\parallel +\parallel x_n\parallel ]}^{\beta }\\ \le & (1-\epsilon )d(x_{n-1},x_n)+K\epsilon \psi (\epsilon ),\end{array}$$

for some $K>0$. Letting $n\to \mathrm{\infty }$, we obtain

$$r\le K\psi (\epsilon ),\text{for every }\epsilon \in [0,1],$$

which implies $r=0$. This leads to a contradiction, therefore

$$\underset{n\to \mathrm{\infty }}{lim}d(x_n,x_{n+1})=0.$$

For $p\ge 1$, suppose there exists j, $0\le j\le m-1$, such that $(n+p)-n+j=1modm$, i.e., $p+j=1modm$. Now, let p be fixed, $j=0$ and let

$$q_n=n^{\alpha }d(x_n,x_{n+p}).$$

So, we have

$$q_{n+1}={(n+1)}^{\alpha }d(x_{n+1},x_{n+1+p})={(n+1)}^{\alpha }d(f(x_n),f(x_{n+p})).$$

Since $p=1modm$, $x_n$ and $x_{n+p}$ lie in different sets $A_i$ and $A_{i+1}$, for some $1\le i\le m$. Then by (2.1) we have

$$q_{n+1}={(n+1)}^{\alpha }(1-\epsilon )d(x_n,x_{n+p})+C{(n+1)}^{\alpha }{\epsilon }^{\alpha }\psi (\epsilon ),$$

(2.3)

where $C=sup\gamma {(1+2c_n)}^{\beta }<\mathrm{\infty }$. Choosing for each n

$$\epsilon =1-{\left(\frac{n}{n+1}\right)}^{\alpha }\le \frac{\alpha }{n+1},$$

the relation (2.3) becomes

$$q_{n+1}\le n^{\alpha }d(x_n,x_{n+p})+C{\alpha }^{\alpha }\psi \left(\frac{\alpha }{n+1}\right)=q_n+C{\alpha }^{\alpha }\psi \left(\frac{\alpha }{n+1}\right).$$

Since $q_0=0$, it follows that

$$q_n=\sum _{k=1}^n(q_k-q_{k-1})\le \sum _{k=1}^{n}C{\alpha }^{\alpha }\psi \left(\frac{\alpha }{k}\right)=C{\alpha }^{\alpha }\sum _{k=1}^n\psi \left(\frac{\alpha }{k}\right).$$

Consequently,

$$d(x_n,x_{n+p})\le C{\left(\frac{\alpha }{n}\right)}^{\alpha }\sum _{k=1}^n\psi \left(\frac{\alpha }{k}\right).$$

This shows that $\{x_n\}$ is a Cauchy sequence in the complete metric space $(Y,d)$ and, thus, it is convergent to a point $y\in Y={\bigcup }_{i=1}^m{A}_i$. The case $j\ne 0$ similar.

On the other hand, the sequence $\{x_n\}$ has an infinite number of terms in each $A_i$, for every $i\in \{1,\dots ,m\}$. Since $(Y,d)$ is complete, in each $A_i$, $i\in \{1,\dots ,m\}$ we can construct a subsequence of $\{x_n\}$ which converges to y. Since each $A_i$ is closed for $i\in \{1,\dots ,m\}$, we get that $y\in {\bigcap }_{i=1}^m{A}_i$. Then ${\bigcap }_{i=1}^m{A}_i\ne \mathrm{\varnothing }$ and we can consider the restriction

which satisfies the conditions of Theorem 1 in [8], since ${\bigcap }_{i=1}^m{A}_i$ is also closed and complete. From this result, it follows that g has a unique fixed point, say $x^{\ast }\in {\bigcap }_{i=1}^m{A}_i$.

We claim now that for any initial value $x\in Y$, we get the same limit point $x^{\ast }\in {\bigcap }_{i=1}^m{A}_i$. Indeed, for $x\in Y={\bigcup }_{i=1}^m{A}_i$, by repeating the above process, the corresponding iterative sequence yields that g has a unique fixed point, say $z\in {\bigcap }_{i=1}^m{A}_i$. Since $x^{\ast }$, $z\in {\bigcap }_{i=1}^m{A}_i$, we have $x^{\ast }$, $z\in A_i$ for all $i\in \{1,\dots ,m\}$ and, hence, $d(x^{\ast },z)$ and $d(f(x^{\ast }),f(z))$ are well defined. We can write (2.1) in the form

$$d(x^{\ast },z)=d(f\left(x^{\ast }\right),f(z))\le (1-\epsilon )d(x^{\ast },z)+K\epsilon \psi (\epsilon ),$$

for some $K>0$. Suppose that $\epsilon =0$. Then we have

$$d(f\left(x^{\ast }\right),f(z))\le d(x^{\ast },z).$$

If equality occurs, the relation

$$d(x^{\ast },z)\le K\psi (\epsilon )$$

is valid for every $\epsilon \in [0,1]$, which implies $d(x^{\ast },z)=0$. Thus, $x^{\ast }$ is the unique fixed point of f for any initial value $x\in Y$.

To prove that the Picard iteration converges to $x^{\ast }$, let us consider $x_1\in Y={\bigcup }_{i=1}^m{A}_i$. Then there exists $i_0\in \{1,\dots ,m\}$ such that $x_n\in A_{i_0}$. As $x^{\ast }\in {\bigcap }_{i=1}^m{A}_i$ it follows that $x^{\ast }\in A_{i_0+1}$ as well. By the continuity of f, we obtain

$$d(f^{n-1}(x_1),x^{\ast })=d(f(x_{n-1}),x^{\ast })=d(x_n,x^{\ast })=\underset{p\to \mathrm{\infty }}{lim}d(x_n,x_{n+p})\le C{\left(\frac{\alpha }{n}\right)}^{\alpha }\sum _{k=1}n\psi \left(\frac{\alpha }{k}\right).$$

Letting $n\to \mathrm{\infty }$, it follows that $(x_n)\to x^{\ast }$, i.e., the Picard iteration converges to the unique fixed point of f for any initial point $x_1\in Y$.

• (ii) Since $x^{\ast }$ is a fixed point and $x^{\ast }\in {\bigcap }_{i=1}^m{A}_i$, we obtain that

  $$d(x_n,x^{\ast })=d(f(x_{n-1}),f\left(x^{\ast }\right))\le d(x_{n-1},x^{\ast })\le \cdots \le d(x_1,x^{\ast })=\parallel x^{\ast }\parallel .$$

  (2.4)

By (2.4), it follows that

$$d(x_n,x_1)\le d(x_n,x^{\ast })+d(x^{\ast },x_1)\le \parallel x^{\ast }\parallel +d(x^{\ast },x_1)\le 2\parallel x^{\ast }\parallel .$$

 □

In view of Remark 1.1, we immediately obtain the following corollary.

Corollary 2.3 (Kirk, Srinivasan, Veeramani [2], Theorem 1.3])

Let $(X,d)$ be a complete metric space, m be a positive integer, $A_1,\dots ,A_m$ be closed nonempty subsets of X, $Y:={\bigcup }_{i=1}^m{A}_i$ and $f:Y\to Y$ be an operator. Assume that:

• (i) ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of Y with respect to f;

• (ii) there exists $\lambda \in [0,1)$ such that, for any $x\in A_i$, $y\in A_{i+1}$, where $A_{m+1}=A_1$, we have

  $$d(f(x),f(y))\le \lambda d(x,y).$$

Then f has a unique fixed point $x^{\ast }\in {\bigcap }_{i=1}^m{A}_i$.

Finally, we will prove a periodic point theorem. For this purpose, notice first that if f satisfies (1.2) with constants α, β, γ and function ψ, and if $\parallel f(x)\parallel \le \parallel x\parallel$ for each $x\in X$, then its m-iterate $f^m$ also satisfies the condition (1.2) with constants α, β, mγ and function ψ. Indeed, let us suppose that f satisfies (1.2) with constants α, β, γ. Then, for every $\epsilon \in [0,1]$, we have

$$\begin{array}{c}d(f^2(x),f^2(y))\hfill \\ \le (1-\epsilon )d(f(x),f(y))+\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+\parallel f(x)\parallel +\parallel f(y)\parallel ]}^{\beta }\hfill \\ \le (1-\epsilon )[(1-\epsilon )d(x,y)+\gamma {\epsilon }^{\alpha }\psi (\epsilon ){(1+\parallel x\parallel +\parallel y\parallel )}^{\beta }]\hfill \\ +\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+\parallel f(x)\parallel +\parallel f(y)\parallel ]}^{\beta }\hfill \\ \le (1-\epsilon )[(1-\epsilon )d(x,y)+\gamma {\epsilon }^{\alpha }\psi (\epsilon ){(1+\parallel x\parallel +\parallel y\parallel )}^{\beta }]\hfill \\ +\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+\parallel x\parallel +\parallel y\parallel ]}^{\beta }\hfill \\ ={(1-\epsilon )}^{2}d(x,y)+(1-\epsilon )\gamma {\epsilon }^{\alpha }\psi (\epsilon ){(1+\parallel x\parallel +\parallel y\parallel )}^{\beta }\hfill \\ +\gamma {\epsilon }^{\alpha }\psi (\epsilon ){[1+\parallel x\parallel +\parallel y\parallel ]}^{\beta }\hfill \\ ={(1-\epsilon )}^{2}d(x,y)+(2-\epsilon )\gamma {\epsilon }^{\alpha }\psi (\epsilon ){(1+\parallel x\parallel +\parallel y\parallel )}^{\beta }\hfill \\ \le (1-\epsilon )d(x,y)+2\gamma {\epsilon }^{\alpha }\psi (\epsilon ){(1+\parallel x\parallel +\parallel y\parallel )}^{\beta }.\hfill \end{array}$$

Thus, we immediately get that, for $m\in \mathbb{N}$ with $m\ge 2$, we have

$$d(f^m(x),f^m(y))\le (1-\epsilon )d(x,y)+m\gamma {\epsilon }^{\alpha }\psi (\epsilon ){(1+\parallel x\parallel +\parallel y\parallel )}^{\beta }.$$

Notice also that if ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of X with respect to f, then each $A_i$ ($i\in \{1,2,\dots ,m\}$) is an invariant set with respect to $f^m$. Using these two remarks, we get the following periodic point theorem.

Theorem 2.4 Let $(X,d)$ be a complete metric space, m be a positive integer, $A_1,\dots ,A_m$ be nonempty subsets of X, $Y:={\bigcup }_{i=1}^m{A}_i$, $\psi :[0,1]\to [0,\mathrm{\infty })$ be an increasing function vanishing with continuity at zero and $f:Y\to Y$ be an operator such that $\parallel f(x)\parallel \le \parallel x\parallel$ for each $x\in Y$. Assume that:

• 1. ${\bigcup }_{i=1}^m{A}_i$ is a cyclic representation of Y with respect to f.

• 2. There exists $i_0\in \{1,\dots ,m\}$ such that $A_{i_0}$ is closed.

• 3. For every $\epsilon \in [0,1]$ and each $x,y\in A_{i_0}$, we have

  

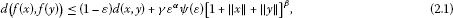
where $\gamma \ge 0$, $\alpha \ge 1$ and $\beta \in [0,\alpha ]$ are fixed constants.

Then, $f^m$ has a fixed point.

Proof Notice that, by the above considerations, $f^m$ is a self mapping on $A_{i_0}$ and it satisfies the condition (1.2) with constants α, β, mγ and function ψ. Thus, by Theorem 1 in [8] we get the conclusion. □