- Research
- Open access
- Published:
The shrinking projection method for solving generalized equilibrium problems and common fixed points for asymptotically quasi-ϕ-nonexpansive mappings
Fixed Point Theory and Applications volume 2011, Article number: 9 (2011)
Abstract
In this article, we introduce a new hybrid projection iterative scheme based on the shrinking projection method for finding a common element of the set of solutions of the generalized mixed equilibrium problems and the set of common fixed points for a pair of asymptotically quasi-ϕ-nonexpansive mappings in Banach spaces and set of variational inequalities for an α-inverse strongly monotone mapping. The results obtained in this article improve and extend the recent ones announced by Matsushita and Takahashi (Fixed Point Theory Appl. 2004(1):37-47, 2004), Qin et al. (Appl. Math. Comput. 215:3874-3883, 2010), Chang et al. (Nonlinear Anal. 73:2260-2270, 2010), Kamraksa and Wangkeeree (J. Nonlinear Anal. Optim.: Theory Appl. 1(1):55-69, 2010) and many others.
AMS Subject Classification: 47H05, 47H09, 47J25, 65J15.
1. Introduction
Let E be a Banach space with norm ||·||, C be a nonempty closed convex subset of E, and let E* denote the dual of E. Let f : C × C → ℝ be a bifunction, φ: C → ℝ be a real-valued function, and B : C → E* be a mapping. The generalized mixed equilibrium problem, is to find x ∈ C such that

The set of solutions to (1.1) is denoted by GMEP(f, B, φ), i.e.,

If B ≡ 0, then the problem (1.1) reduces into the mixed equilibrium problem for f, denoted by MEP(f, φ), is to find x ∈ C such that

If φ ≡ 0, then the problem (1.1) reduces into the generalized equilibrium problem, denoted by GEP(f, B), is to find x ∈ C such that

If f ≡ 0, then the problem (1.1) reduces into the mixed variational inequality of Browder type, denoted by MVI(B, C), is to find x ∈ C such that

If φ ≡ 0, then the problem (1.5) reduces into the classical variational inequality, denoted by VI(B, C), which is to find x ∈ C such that

If B ≡ 0 and φ ≡ 0, then the problem (1.1) reduces into the equilibrium problem for f, denoted by EP(f), which is to find x ∈ C such that

If f ≡ 0, then the problem (1.3) reduces into the minimize problem, denoted by Argmin (φ), which is to find x ∈ C such that

The above formulation (1.6) was shown in [1] to cover monotone inclusion problems, saddle point problems, variational inequality problems, minimization problems, optimization problems, variational inequality problems, vector equilibrium problems, and Nash equilibria in noncooperative games. In addition, there are several other problems, for example, the complementarity problem, fixed point problem and optimization problem, which can also be written in the form of an EP(f). In other words, the EP(f) is an unifying model for several problems arising in physics, engineering, science, optimization, economics, etc. In the last two decades, many articles have appeared in the literature on the existence of solutions of EP(f); see, for example [1–4] and references therein. Some solution methods have been proposed to solve the EP(f) in Hilbert spaces and Banach spaces; see, for example [5–20] and references therein.
A Banach space E is said to be strictly convex if  < 1 for all x, y ∈ E with ||x|| = ||y|| = 1 and x ≠ y. Let U = {x ∈ E : ||x|| = 1} be the unit sphere of E. Then, a Banach space E is said to be smooth if the limit
< 1 for all x, y ∈ E with ||x|| = ||y|| = 1 and x ≠ y. Let U = {x ∈ E : ||x|| = 1} be the unit sphere of E. Then, a Banach space E is said to be smooth if the limit  exists for each x, y ∈ U. It is also said to be uniformly smooth if the limit exists uniformly in x, y ∈ U. Let E be a Banach space. The modulus of convexity of E is the function δ : [0, 2] → [0, 1] defined by
exists for each x, y ∈ U. It is also said to be uniformly smooth if the limit exists uniformly in x, y ∈ U. Let E be a Banach space. The modulus of convexity of E is the function δ : [0, 2] → [0, 1] defined by

A Banach space E is uniformly convex if and only if δ (ε) > 0 for all ε ∈ (0, 2]. Let p be a fixed real number with p ≥ 2. A Banach space E is said to be p-uniformly convex if there exists a constant c > 0 such that δ (ε) ≥ cεp for all ε ∈ [0, 2]; see [21, 22] for more details. Observe that every p-uniformly convex is uniformly convex. One should note that no Banach space is p-uniformly convex for 1 < p < 2. It is well known that a Hilbert space is 2-uniformly convex, uniformly smooth. For each p > 1, the generalized duality mapping J p : E → 2E*is defined by

for all x ∈ E. In particular, J = J2 is called the normalized duality mapping. If E is a Hilbert space, then J = I, where I is the identity mapping.
A set valued mapping U : E ⇉ E* with graph G(U) = {(x, x*) : x* ∈ Ux}, domain D(U) = {x ∈ E : Ux ≠ ∅}, and rang R(U) = ∪{Ux : x ∈ D(U)}. U is said to be monotone if 〈x - y, x* - y*〉 ≥ 0 whenever x* ∈ Ux, y* ∈ Uy. A monotone operator U is said to be maximal monotone if its graph is not properly contained in the graph of any other monotone operator. We know that if U is maximal monotone, then the solution set U-1 0 = {x ∈ D(U) : 0 ∈ Ux} is closed and convex. It is knows that U is a maximal monotone if and only if R(J + rU) = E* for all r > 0 when E is a reflexive, strictly convex and smooth Banach space (see [23]).
Recall that let A : C → E* be a mapping. Then, A is called
-
(i)
monotone if
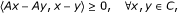
-
(ii)
α-inverse-strongly monotone if there exists a constant α > 0 such that
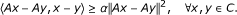
The class of inverse-strongly monotone mappings has been studied by many researchers to approximating a common fixed point; see [24–29] for more details.
Recall that a mappings T : C → C is said to be nonexpansive if

T is said to be quasi-nonexpansive if F(T) ≠ ∅, and

T is said to be asymptotically nonexpansive if there exists a sequence {k n } ⊂ [1, ∞) with k n → 1 as n → ∞ such that

T is said to be asymptotically quasi-nonexpansive if F(T) ≠ ∅ and there exists a sequence {k n } ⊂ [1, ∞) with k n → 1 as n → ∞ such that

T is called uniformly L-Lipschitzian continuous if there exists L > 0 such that

The class of asymptotically nonexpansive mappings was introduced by Goebel and Kirk [30] in 1972. Since 1972, a host of authors have studied the weak and strong convergence of iterative processes for such a class of mappings.
If C is a nonempty closed convex subset of a Hilbert space H and P C : H → C is the metric projection of H onto C, then P C is a nonexpansive mapping. This fact actually characterizes Hilbert spaces and, consequently, it is not available in more general Banach spaces. In this connection, Alber [31] recently introduced a generalized projection operator C in Banach space E which is an analogue of the metric projection in Hilbert spaces.
Let E be a smooth, strictly convex and reflexive Banach spaces and C be a nonempty, closed convex subset of E. We consider the Lyapunov functional ϕ : E × E → ℝ+ defined by

for all x, y ∈ E, where J is the normalized duality mapping from E to E*.
Observe that, in a Hilbert space H, (1.9) reduces to ϕ(y, x) = ||x - y||2 for all x, y ∈ H. The generalized projection Π C : E → C is a mapping that assigns to an arbitrary point x ∈ E the minimum point of the functional ϕ(y, x); that is, Π C x = x*, where x* is the solution to the minimization problem:

The existence and uniqueness of the operator Π C follows from the properties of the functional ϕ(y, x) and strict monotonicity of the mapping J (see, for example, [9, 32–34]). In Hilbert spaces, Π C = P C .. It is obvious from the definition of the function ϕ that
-
(1)
(||y|| - ||x||)2 ≤ ϕ(y, x) ≤ (||y|| + ||x||)2 for all x, y ∈ E.
-
(2)
ϕ(x, y) = ϕ (x, z) + ϕ (z, y) + 2 〈x - z, Jz - Jy〉 for all x, y, z ∈ E.
-
(3)
ϕ(x, y) = 〈x, Jx - Jy〉 + 〈y - x, Jy〉 ≤ ||x|| ||Jx - Jy|| + ||y - x|| ||y|| for all x, y ∈ E.
-
(4)
If E is a reflexive, strictly convex and smooth Banach space, then, for all x, y ∈ E,
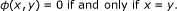
By the Hahn-Banach theorem, J(x) ≠ ∅ for each x ∈ E, for more details see [35, 36].
Remark 1.1. It is also known that if E is uniformly smooth, then J is uniformly norm-to-norm continuous on each bounded subset of E. Also, it is well known that if E is a smooth, strictly convex and reflexive Banach space, then the normalized duality mapping J : E → 2E*is single-valued, one-to-one and onto (see [35]).
Let C be a closed convex subset of E, and let T be a mapping from C into itself. We denote by F(T) the set of fixed point of T. A point p in C is said to be an asymptotic fixed point of T[37] if C contains a sequence {x
n
} which converges weakly to p such that limn →∞||x
n
- Tx
n
|| = 0. The set of asymptotic fixed points of T will be denoted by  .
.
A point p in C is said to be a strong asymptotic fixed point of T[37] if C contains a sequence {x
n
} which converges strong to p such that limn→∞||x
n
- Tx
n
|| = 0. The set of strong asymptotic fixed points of S will be denoted by  .
.
A mapping T is called relatively nonexpansive[38–40] if  and
and

The asymptotic behavior of relatively nonexpansive mappings were studied in [38, 39].
A mapping T : C → C is said to be weak relatively nonexpansive if  and
and

A mapping T is called hemi-relatively nonexpansive if F(T) ≠ ∅ and

A mapping T is said to be relatively asymptotically nonexpansive[32, 41] if  and there exists a sequence {k
n
} ⊂ [0, ∞) with k
n
→ 1 as n → ∞ such that
and there exists a sequence {k
n
} ⊂ [0, ∞) with k
n
→ 1 as n → ∞ such that

Remark 1.2. Obviously, relatively nonexpansive implies weak relatively nonexpansive and both also imply hemi-relatively nonexpansive. Moreover, the class of relatively asymptotically nonexpansive is more general than the class of relatively nonexpansive mappings.
We note that hemi-relatively nonexpansive mappings are sometimes called quasi-ϕ-nonexpansive mappings.
We recall the following :
-
(i)
T : C → C is said to be ϕ-nonexpansive [42, 43] if ϕ (Tx, Ty) ≤ ϕ (x, y) for all x, y ∈ C.
-
(ii)
T : C → C is said to be quasi-ϕ-nonexpansive [42, 43] if F(T) ≠ ∅ and ϕ(p, Tx) ≤ ϕ(p, x) for all x ∈ C and p ∈ F(T).
-
(iii)
T : C → C is said to be asymptotically ϕ-nonexpansive [43] if there exists a sequence {k n } ⊂ [0, ∞) with k n → 1 as n → ∞ such that ϕ (Tnx, Tny) ≤ k n ϕ(x, y) for all x, y ∈ C.
-
(iv)
T : C → C is said to be asymptotically quasi-ϕ-nonexpansive [43] if F(T) ≠ ∅ and there exists a sequence {k n } ⊂ [0, ∞) with k n → 1 as n → ∞ such that ϕ(p, Tnx) ≤ k n ϕ (p, x) for all x ∈ C, p ∈ F(T) and n ≥ 1.
Remark 1.3. (i) The class of (asymptotically) quasi-ϕ-nonexpansive mappings is more general than the class of relatively (asymptotically) nonexpansive mappings, which requires the strong restriction  .
.
-
(ii)
In real Hilbert spaces, the class of (asymptotically) quasi-ϕ-nonexpansive mappings is reduced to the class of (asymptotically) quasi-nonexpansive mappings.
Let T be a nonlinear mapping, T is said to be uniformly asymptotically regular on C if

T : C → C is said to be closed if for any sequence {x n } ⊂ C such that limn→∞x n = x0 and limn→∞Tx n = y0, then Tx0 = y0.
We give some examples which are closed and asymptotically quasi-ϕ-nonexpansive.
Example 1.4. (1). Let E be a uniformly smooth and strictly convex Banach space and U ⊂ E × E* be a maximal monotone mapping such that its zero set U-10 is nonempty. Then, J r = (J + rU)-1J is a closed and asymptotically quasi-ϕ-nonexpansive mapping from E onto D(U) and F(J r ) = U-10.
(2). Let Π C be the generalized projection from a smooth, strictly convex and reflexive Banach space E onto a nonempty closed and convex subset C of E. Then Π C is a closed and asymptotically quasi-ϕ-nonexpansive mapping from E onto C with F(Π C ) = C.
Recently, Matsushita and Takahashi [44] obtained the following results in a Banach space.
Theorem MT. Let E be a uniformly convex and uniformly smooth Banach space, let C be a nonempty closed convex subset of E, let T be a relatively nonexpansive mapping from C into itself, and let {α n } be a sequence of real numbers such that 0 ≤ α n < 1 and lim supn→∞< 1. Suppose that {x n } is given by

where J is the duality mapping on E. If F(T) is nonempty, then {x n } converges strongly to P F (T) x , where PF(T)is the generalized projection from C onto F(T). In 2008, Iiduka and Takahashi [45] introduced the following iterative scheme for finding a solution of the variational inequality problem for an inverse-strongly monotone operator A in a 2-uniformly convex and uniformly smooth Banach space E : x1 = x ∈ C and

for every n = 1, 2, 3,..., where Π C is the generalized metric projection from E onto C, J is the duality mapping from E into E* and {λ n } is a sequence of positive real numbers. They proved that the sequence {x n } generated by (1.12) converges weakly to some element of VI(A, C).
A popular method is the shrinking projection method which introduced by Takahashi et al. [46] in year 2008. Many authors developed the shrinking projection method for solving (mixed) equilibrium problems and fixed point problems in Hilbert and Banch spaces; see, [12, 15, 16, 47–57] and references therein.
Recently, Qin et al. [58] further extended Theorem MT by considering a pair of asymptotically quasi-ϕ-nonexpansive mappings. To be more precise, they proved the following results.
Theorem QCK. Let E be a uniformly smooth and uniformly convex Banach space and C a nonempty closed and convex subset of E. Let T : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence  such that
such that  as n → ∞ and S : C → C a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence
as n → ∞ and S : C → C a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence  such that
such that  as n → ∞. Let {α
n
}, {β
n
}, {γ
n
} and {δ
n
} be real number sequences in [0, 1].
as n → ∞. Let {α
n
}, {β
n
}, {γ
n
} and {δ
n
} be real number sequences in [0, 1].
Assume that T and S are uniformly asymptotically regular on C and Ω = F(T) ∩ F(S) is nonempty and bounded. Let {x n } be a sequence generated in the following manner:

where  for each n ≥ 1, J is the duality mapping on E, and M
n
= sup{ϕ(z, x
n
) : z ∈ Ω } for each n ≥ 1. Assume that the control sequences {α
n
}, {β
n
}, {γ
n
} and {δ
n
} satisfy the following restrictions :
for each n ≥ 1, J is the duality mapping on E, and M
n
= sup{ϕ(z, x
n
) : z ∈ Ω } for each n ≥ 1. Assume that the control sequences {α
n
}, {β
n
}, {γ
n
} and {δ
n
} satisfy the following restrictions :
-
(a)
β n + γ n + δ n = 1, ∀n ≥ 1;
-
(b)
lim infn→∞ γ n δ n , limn→∞ β n = 0;
-
(c)
0 ≤ α n < 1 and lim supn→∞ α n < 1.
On the other hand, Chang, Lee and Chan [59] proved a strong convergence theorem for finding a common element of the set of solutions for a generalized equilibrium problem (1.4) and the set of common fixed points for a pair of relatively nonexpansive mappings in Banach spaces. They proved the following results.
Theorem CLC. Let E be a uniformly smooth and uniformly convex Banach space, C be a nonempty closed convex subset of E. Let A : C → E* be a α-inverse-strongly monotone mapping and f : C × C → ℝ be a bifunction satisfying the conditions (A 1) - (A 4). Let S, T : C → C be two relatively nonexpansive mappings such that Ω := F(T) ∩ F(S) ∩ GEP(f, A). Let {x n } be the sequence generated by

where {α n } and {β n } are sequences in [0, 1] and {γ n } ⊂ [a, 1) for some a > 0. If the following conditions are satisfied
-
(a)
lim infn →∞ α n (1 - α n ) > 0;
-
(b)
lim infn →∞ β n (1 -β n ) > 0;
then, {x n } converges strongly to ΠΩx0, where ΠΩ is the generalized projection of E onto Ω.
Very recently, Kim [60], considered the shrinking projection methods which were introduced by Takahashi et al. [46] for asymptotically quasi-ϕ-nonexpansive mappings in a uniformly smooth and strictly convex Banach space which has the Kadec-Klee property.
In this article, motivated and inspired by the study of Matsushita and Takahashi [44], Qin et al. [58], Kim [60], and Chang et al. [59], we introduce a new hybrid projection iterative scheme based on the shrinking projection method for finding a common element of the set of solutions of the generalized mixed equilibrium problems, the set of the variational inequality and the set of common fixed points for a pair of asymptotically quasi-ϕ-nonexpansive mappings in Banach spaces. The results obtained in this article improve and extend the recent ones announced by Matsushita and Takahashi [44], Qin et al. [58], Chang et al. [59] and many others.
2. Preliminaries
For the sake of convenience, we first recall some definitions and conclusions which will be needed in proving our main results.
In the sequel, we denote the strong convergence, weak convergence and weak* convergence of a sequence {x n } by x n → x, x n ⇀* × and x n ⇀* x, respectively.
It is well known that a uniformly convex Banach space has the Kadec-Klee property, i.e. if x n ⇀ x and ||x n || → ||x||, then x n → x.
Lemma 2.1. ([31, 61]) Let E be a smooth, strictly convex and reflexive Banach space and C be anonempty closed convex subset. Then, the following conclusion hold:

Lemma 2.2. ([34]). If E be a 2-uniformly convex Banach space and 0 < c ≤ 1. Then, for all x, y ∈ E we have

where J is the normalized duality mapping of E.
The best constant  in Lemma is called the p-uniformly convex constant of E.
in Lemma is called the p-uniformly convex constant of E.
Lemma 2.3. ([62]). If E be a p-uniformly convex Banach space and p be a given real number with p ≥ 2, then for all x, y ∈ E, j x ∈ J p x and j y ∈ J p y

where J
p
is the generalized duality mapping of E and is the p-uniformly convexity constant of E.
is the p-uniformly convexity constant of E.
Lemma 2.4. ([63]) Let E be a uniformly convex Banach space and B r (0) a closed ball of E. Then, there exists a continuous strictly increasing convex function g : [0, ∞) → [0, ∞) with g(0) = 0 such that

for all x, y ∈ B r (0) and α ∈ [0, 1].
Lemma 2.5. ([58]) Let E be a uniformly convex and smooth Banach space, C a nonempty closed convex subset of E and T : C → C a closed asymptotically quasi-ϕ-nonexpansive mapping. Then, F(T) is a closed convex subset of C.
Lemma 2.6. ([61]) Let E be a smooth and uniformly convex Banach space. Let x n and y n be sequences in E such that either {x n } or {y n } is bounded. If limn→∞ϕ(x n , y n ) = 0, then limn→∞||x n - y n || = 0.
Lemma 2.7. (Alber[31]). Let C be a nonempty closed convex subset of a smooth Banach space E and x ∈ E. Then, x0 = Π C x if and only if

Let E be a reflexive, strictly convex, smooth Banach space and J the duality mapping from E into E*. Then, J-1 is also single valued, one-to-one, surjective, and it is the duality mapping from E* into E. We make use of the following mapping V studied in Alber [31]

for all x ∈ E and x* ∈ E*; that is, V (x, x*) = ϕ(x, J-1x*).
Lemma 2.8. (Kohsaka and Takahashi [[64], Lemma 3.2]). Let E be a reflexive, strictly convex smooth Banach space and let V be as in (2.1). Then,

for all × ∈ E and x*, y* ∈ E*.
Proof. Let x ∈ E. Define g(x*) = V (x, x*) and f(x*) = ||x*||2 for all x* ∈ E*. Since J-1 is the duality mapping from E* to E, we have

Hence, we get

that is,

for all x*, y* ∈ E*.
For solving the generalized equilibrium problem, let us assume that the nonlinear mapping A : C → E* is α-inverse strongly monotone and the bifunction f : C × C → ℝ satisfies the following conditions:
(A1) f(x, x) = 0 ∀x ∈ C;
(A2) f is monotone, i.e., f(x, y) + f(y, x) ≤ 0, ∀x, y ∈ C;
(A3) lim supt↓0f (x + t(z - x), y) ≤ f(x, y), ∀x, y, z ∈ C;
(A4) the function y ↦ f(x, y) is convex and lower semicontinuous.
Lemma 2.9. ([1]) Let E be a smooth, strictly convex and reflexive Banach space and C be a nonempty closed convex subset of E. Let f : C × C → ℝ be a bifunction satisfying the conditions (A 1) - (A 4). Let r > 0 and × ∈ E, then there exists z ∈ C such that

Lemma 2.10. ([65]) Let C be a closed convex subset of a uniformly smooth and strictly convex Banach space E and let f be a bifunction from C × C to ℝ satisfying (A 1) - (A 4). For r > 0 and × ∈ E, define a mapping T r : E → C as follows:

for all × ∈ C. Then, the following conclusions holds:
-
(1)
T r is single-valued;
-
(2)
T r is a firmly nonexpansive-type mapping, i.e.
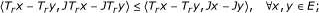
(A3) F(T r ) = EP(f );
(A4) EP(f) is a closed convex.
Lemma 2.11. ([19]) Let C be a closed convex subset of a smooth, strictly convex and reflexive Banach space E, let f be a bifunction from C × C to ℝ satisfying (A 1) - (A 4) and let r > 0. Then, for × ∈ E and q ∈ F(T r ),

Lemma 2.12. ([66]) Let C be a closed convex subset of a smooth, strictly convex and reflexive Banach space E. Let B : C → E* be a continuous and monotone mapping, φ : C → ℝ be a lower semi-continuous and convex function, and f be a bifunction from C × C to ℝ satisfying (A 1) - (A 4). For r > 0 and × ∈ E, then there exists u ∈ C such that

Define a mapping K r : C → C as follows:

for all x ∈ C. Then, the following conclusions holds:
-
(a)
K r is single-valued ;
-
(b)
K r is a firmly nonexpansive-type mapping, i.e.;
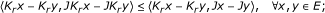
-
(c)
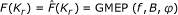 ;
; -
(d)
GMEP(f, B, φ) is a closed convex,
-
(e)
ϕ(q, K r z) + ϕ(K r z, z) ≤ ϕ(q, z), ∀q ∈ F (K r ), z ∈ E.
Remark 2.13. ([66]) It follows from Lemma 2.12 that the mapping K r : C → C defined by (2.3) is a relatively nonexpansive mapping. Thus, it is quasi-ϕ-nonexpansive.
Let C be a nonempty closed convex subset of a Banach space E and let A be an inverse-strongly monotone mapping of C into E* which is said to be hemicontinuous if for all x, y ∈ C, the mapping F of [0, 1] into E*, defined by F(t) = A(tx + (1 - t)y), is continuous with respect to the weak* topology of E*. We define by N C (v) the normal cone for C at a point v ∈ C, that is,

Lemma 2.14. (Rockafellar[23]). Let C be a nonempty, closed convex subset of a Banach space E, and A a monotone, hemicontinuous operator of C into E*. Let U : E ⇉ E* be an operator defined as follows:

Then, U is maximal monotone and U-10 = VI(A, C).
3. Main results
In this section, we shall prove a strong convergence theorem for finding a common element of the set of solutions for a generalized mixed equilibrium problem (1.2), set of variational inequalities for an α-inverse strongly monotone mapping and the set of common fixed points for a pair of asymptotically quasi-ϕ-nonexpansive mappings in Banach spaces.
Theorem 3.1. Let E be a uniformly smooth and 2-uniformly convex Banach space, C be a nonempty closed convex subset of E. Let A be an α-inverse-strongly monotone mapping of C into E* satisfying ||Ay|| ≤ ||Ay - Au||, ∀y ∈ C and u ∈ VI(A, C) ≠ ∅. Let B : C → E* be a continuous and monotone mapping and f : C × C → ℝ be a bifunction satisfying the conditions (A 1) - (A 4), and φ : C → ℝ be a lower semi-continuous and convex function. Let T : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence such that
such that as n → ∞ and S : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence
as n → ∞ and S : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence such that
such that as n → ∞. Assume that T and S are uniformly asymptotically regular on C and Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ GMEP(f, B, φ.) ≠ ∅.
as n → ∞. Assume that T and S are uniformly asymptotically regular on C and Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ GMEP(f, B, φ.) ≠ ∅.
Let {x n } be the sequence defined by x0 ∈ E and

where  as n → ∞,
as n → ∞,  for each n ≥ 1, M
n
= sup{ϕ(z, x
n
) : z ∈ Ω } for each n ≥ 1, {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where
for each n ≥ 1, M
n
= sup{ϕ(z, x
n
) : z ∈ Ω } for each n ≥ 1, {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where  is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied: lim infn→∞(1 -α
n
) > 0 and lim infn→∞(1 -β
n
) > 0. Then, the sequence {x
n
} converges strongly to ΠΩx0, where ΠΩ is generalized projection of E onto Ω.
is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied: lim infn→∞(1 -α
n
) > 0 and lim infn→∞(1 -β
n
) > 0. Then, the sequence {x
n
} converges strongly to ΠΩx0, where ΠΩ is generalized projection of E onto Ω.
Proof. We have several steps to prove this theorem as follows:
Step 1. We first show that Cn+1is closed and convex for each n ≥ 1. Indeed, it is obvious that C1 = C is closed and convex. Suppose that C i is closed and convex for each i ∈ ℕ. Next, we prove that Ci+1is closed and convex. For any z ∈ Ci+1, we know that ϕ(z, u i ) ≤ ϕ (z, x i ) + θ i is equivalent to

where  and M
i
= sup{ϕ(z, x
i
) : z ∈ Ω} for each i ≥ 1. Hence, Ci+1is closed and convex. Then, for each n ≥ 1, we see that C
n
is closed and convex. Hence,
and M
i
= sup{ϕ(z, x
i
) : z ∈ Ω} for each i ≥ 1. Hence, Ci+1is closed and convex. Then, for each n ≥ 1, we see that C
n
is closed and convex. Hence,  is well defined.
is well defined.
By the same argument as in the proof of [[43], Lemma 2.4], one can show that F(T) ∩ F(S) is closed and convex. We also know that VI(A, C) = U-10 is closed and convex, and hence from Lemma 2.12(d), Ω := F(S) ∩ F(T) ∩ VI(A, C) ∩ GMEP(f, B, φ) is a nonempty, closed and convex subset of C. Consequently, ΠΩ is well defined.
Step 2. We show that the sequence {x n } is well defined. Next, we prove that Ω ⊂ C n for each n ≥ 1. If n = 1, Ω ⊂ C1 = C is obvious. Suppose that Ω ⊂ C i for some positive integer i. For every q ∈ Ω, we obtain from the assumption that q ∈ C i . It follows, from Lemma 2.1 and Lemma 2.8, that

Thus, q ∈ VI(A, C) and A is α-inverse-strongly monotone, we have

From Lemma 2.2 and ||Ay|| ≤ ||Ay - Au|| for all y ∈ C and q ∈ Ω, we obtain

Substituting (3.3) and (3.4) into (3.2), we have

As Ti is asymptotically quasi-ϕ-nonexpansive mapping, we also have

It follows that

This shows that q ∈ Ci+1. This implies that Ω ⊂ C n for each n ≥ 1.
From  , we see that
, we see that

Since Ω ⊂ C n for each n ≥ 1, we arrive at

Hence, the sequence {x n } is well defined.
Step 3. Now, we prove that {x n } is bounded.
In view of Lemma 2.1, we see that

for each q ∈ C n . Therefore, we obtain that the sequence ϕ(x n , x0) is bounded, and so are {x n }, {w n }, {y n }, {z n }, {Tnw n } and {Snx n }.
Step 4. We show that {x n } is a Cauchy sequence.
Since  and
and  , we have
, we have

This implies that {ϕ(x n , x0)} is nondecreasing, and limn →∞ϕ(x n , x0) exists.
For m > n and from Lemma 2.1, we have

Letting m, n → ∞ in (3.9), we see that ϕ(x m , x n ) → 0. It follows from Lemma 2.6 that ||x m - x n || → 0 as m, n → ∞. Hence, {x n } is a Cauchy sequence. Since E is a Banach space and C is closed and convex, we can assume that p ∈ C such that x n → p as n → ∞.
Step 5. We will show that p ∈ Ω:= F(T) ∩ F(S) ∩ VI(A, C) ∩ GMEP(f, B, φ).
(a) First, we show that p ∈ F(T) ∩ F(S).
By taking m = n + 1 in (3.9), we obtain that

Since  , from definition of Cn+1, we have
, from definition of Cn+1, we have

and from (3.5) and (3.6), we also have

Since E is uniformly smooth and uniformly convex, from (3.10)-(3.12), θ n → 0 as n → ∞ and
Lemma 2.6, it follows that

and by using triangle inequality, we have

Since J is uniformly norm-to-norm continuous, we also have

and

Since  , and from (3.7), we have
, and from (3.7), we have

Since ||x n - u n || → 0 and J is uniformly continuous, we have

Since {x n } and {u n } are bounded, it follows from (3.14) and (3.15) that ϕ(y n , u n ) → 0 as n → ∞. Since E is smooth and uniformly convex, from Lemma 2.6, we have

Since J is uniformly norm-to-norm continuous, we also have

Again from (3.1) and (3.16), we have

This implies that ||JTnw n - Jx n || → 0. Again since J-1 is uniformly norm-to-norm continuous, we also have

For p ∈ Ω, we note that

It follows from (3.22) and x n → p as n → ∞, that

On other hand, we have

Since T is uniformly asymptotically regular and from (3.24), we obtain that

Thai is, TTnwn → p as n → ∞. From the closedness of T, we see that p ∈ F(T). Furthermore, For q ∈ Ω, from (3.7) and (3.18) that

and hence

From (3.18) and lim infn→∞(1 -β n ) > 0, obtain that

From Lemma 2.1, Lemma 2.8 and (3.4), we compute

Applying Lemma 2.6 and (3.27) that

Since J is uniformly norm-to-norm continuous on bounded sets, by (3.28), we have

From(3.1), (3.20) and (ii), we have

Since J-1 is uniformly norm-to-norm continuous on bounded sets

We observe that

It follows from (3.31) and x n → p as n → ∞, we obtain

On other hand, we have

Since S is uniformly asymptotically regular and (3.33), we obtain that

that is, SSnz n → p as n → ∞. From the closedness of S, we see that p ∈ F(S). Hence, p ∈ F(T) ∩ F(S).
(b) We show that p ∈ GMEP(f, B, φ). From (A2), we have

and hence

For t with 0 < t ≤ 1 and y ∈ C, let y t = t y + (1 - t)p. Then, we get y t ∈ C. From (3.35), it follows that

we know that y
n
, u
n
→ p as n → ∞, and  as n → ∞. Since B is monotone, we know that 〈By
t
- Bu
n
, y
t
- u
n
〉 ≥ 0. Thus, it follows from (A4) that
as n → ∞. Since B is monotone, we know that 〈By
t
- Bu
n
, y
t
- u
n
〉 ≥ 0. Thus, it follows from (A4) that

Based on the conditions (A1), (A4) and convexity of φ, we have

and hence

From (A3) and the weakly lower semicontinuity of φ, and letting t → 0, we also have

This implies that p ∈ GMEP(f, B, φ).
(c) We show that p ∈ VI(A, C). Indeed, define a set-valued U : E ⇉ E* by Lemma 2.14, U is maximal monotone and U-10 = VI(A, C). Let (v, w) ∈ G(U). Since w ∈ Uv = Av + N C (v), we get w - Av ∈ N C (v).
From w n ∈ C, we have

On the other hand, since  . Then from Lemma 2.7, we have
. Then from Lemma 2.7, we have

and thus

It follows from (3.36) and (3.37) that

where M = supn≥1||v - w n ||. Takeing the limit as n → ∞, (3.28) and (3.29), we obtain 〈v - p, w〉 ≥ 0. Based on the maximality of U, we have p ∈ U-10 and hence p ∈ VI(A, C). Hence, by (a), (b) and (c), we obtain p ∈ Ω.
Step 5. Finally, we prove that p = ΠΩx0. Taking the limit as n → ∞ in (3.8), we obtain that

and hence, p = ΠΩx0 by Lemma 2.1. This completes the proof.
The following Theorems can readily be derived from Theorem 3.1.
Corollary 3.2. Let E be a uniformly smooth and 2-uniformly convex Banach space, and C be a nonempty closed convex subset of E. Let A be an α-inverse-strongly monotone mapping of C into E* satisfying ||Ay|| ≤ ||Ay - Au||, ∀y ∈ C and u ∈ VI(A, C) ≠ Ø,. Let f : C × C → ℝ be a bifunction satisfying the conditions (A 1) - (A 4), and φ : C → ℝ be a lower semi-continuous and convex function. Let T : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence such that
such that as n → ∞ and S : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence
as n → ∞ and S : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence such that
such that as n → ∞. Assume that T and S are uniformly asymptotically regular on C and Ω:= F(T) ∩ F(S) ∩ VI(A, C) ∩ MEP(f, φ) ≠ ∅. Let {x
n
} be the sequence defined by x0 ∈ E and
as n → ∞. Assume that T and S are uniformly asymptotically regular on C and Ω:= F(T) ∩ F(S) ∩ VI(A, C) ∩ MEP(f, φ) ≠ ∅. Let {x
n
} be the sequence defined by x0 ∈ E and

where  as n → ∞,
as n → ∞,  for each n ≥ 1, M
n
= sup{ϕ(z, x
n
) : z ∈ Ω} for each n ≥ 1, {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where
for each n ≥ 1, M
n
= sup{ϕ(z, x
n
) : z ∈ Ω} for each n ≥ 1, {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where  is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
-
(i)
lim infn→∞(1 -α n ) > 0,
-
(ii)
lim infn→∞(1 -β n ) > 0.
Then, the sequence {x n } converges strongly to ΠΩx0, where ΠΩ is generalized projection of E onto Ω.
Proof. Putting B ≡ 0 in Theorem 3.1, the conclusion of Theorem 3.2 can be obtained.
Corollary 3.3. Let E be a uniformly smooth and 2-uniformly convex Banach space, C be a nonempty closed convex subset of E. Let A be an α-inverse-strongly monotone mapping of C into E* satisfying ||Ay|| ≤ ||Ay - Au||, ∀y ∈ C and u ∈ VI(A, C) ≠ Ø. Let B : C → E* be a continuous and monotone mapping and φ : C → ℝ be a lower semi-continuous and convex function. Let T : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence such that
such that as n → ∞ and S : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence
as n → ∞ and S : C → C be a closed and asymptotically quasi-ϕ-nonexpansive mapping with the sequence such that
such that as n → ∞. Assume that T and S are uniformly asymptotically regular on C and Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ MVI(B, C) ≠ ∅. Let {x
n
} be the sequence defined by x0 ∈ E and
as n → ∞. Assume that T and S are uniformly asymptotically regular on C and Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ MVI(B, C) ≠ ∅. Let {x
n
} be the sequence defined by x0 ∈ E and

where  as n → ∞,
as n → ∞,  for each n ≥ 1, M
n
= sup{ϕ(z, x
n
) : z ∈ Ω} for each n ≥ 1, {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where
for each n ≥ 1, M
n
= sup{ϕ(z, x
n
) : z ∈ Ω} for each n ≥ 1, {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where  is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
-
(i)
lim infn→∞(1 -α n ) > 0;
-
(ii)
lim infn→∞(1 -β n ) > 0.
Then, the sequence {x n } converges strongly to ΠΩx0, where ΠΩ is generalized projection of E onto Ω.
Proof. Putting f ≡ 0 in Theorem 3.1, the conclusion of Theorem 3.2 can be obtained.
Since every closed relatively asymptotically nonexpansive mapping is asymptotically quasi-ϕ-nonexpansive, we obtain the following corollary.
Corollary 3.4. Let E be a uniformly smooth and 2-uniformly convex Banach space, C be a nonempty closed convex subset of E. Let A be an α-inverse-strongly monotone mapping of C into E* satisfying ||Ay|| ≤ ||Ay - Au||, ∀y ∈ C and u ∈ VI(A, C) ≠ Ø. Let B : C → E* be a continuous and monotone mapping and f : C × C → ℝ be a bifunction satisfying the conditions (A 1) - (A 4), and φ. C → ℝ be a lower semi-continuous and convex function. Let T. C → C be a closed and relatively asymptotically nonexpansive mapping with the sequence such that
such that as n → ∞ and S. C →C be a closed and relatively asymptotically nonexpansive mapping with the sequence
as n → ∞ and S. C →C be a closed and relatively asymptotically nonexpansive mapping with the sequence such that
such that as n → ∞. Assume that T and S are uniformly asymptotically regular on C and Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ GMEP(f, B,φ) ≠ ∅. Let {x
n
} be the sequence defined by x0 ∈ E and
as n → ∞. Assume that T and S are uniformly asymptotically regular on C and Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ GMEP(f, B,φ) ≠ ∅. Let {x
n
} be the sequence defined by x0 ∈ E and

where as n → ∞,
as n → ∞,  for each n ≥ 1, M
n
= sup{ϕ (z, x
n
). z ∈ Ω} for each n ≥ 1, {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/ 2, where
for each n ≥ 1, M
n
= sup{ϕ (z, x
n
). z ∈ Ω} for each n ≥ 1, {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/ 2, where is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
-
(i)
lim infn→∞(1 - α n ) > 0;
-
(ii)
lim infn→∞(1 - β n ) > 0.
Then, the sequence {x n } converges strongly to ΠΩx0, where ΠΩis generalized projection of E onto Ω.
Since every closed relatively nonexpansive mapping is asymptotically quasi-ϕ-nonexpansive, we obtain the following corollary.
Corollary 3.5. Let E be a uniformly smooth and 2-uniformly convex Banach space, C be a nonempty closed convex subset of E. Let A be an α-inverse-strongly monotone mapping of C into E* satisfying ||Ay|| ≤ ||Ay Au||, ∀y ∈ C and u ∈ VI(A, C) ≠ Ø. Let B : C → E* be a continuous and monotone mapping and f : C × C → ℝ be a bifunction satisfying the conditions (A 1) - (A 4), and φ : C → ℝ be a lower semi-continuous and convex function. Let T, S : C → C be closed relatively nonexpansive mappings such that Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ GMEP(f, B,φ) ≠ ∅. Let {x n } be the sequence defined by x0 ∈ E and

where {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
-
(i)
lim infn→∞(1 - α n ) > 0,
-
(ii)
lim infn→∞(1 - β n ) > 0.
Then, the sequence {x n } converges strongly to ΠΩx0, where ΠΩis generalized projection of E onto Ω.
Corollary 3.6. Let E be a uniformly smooth and 2-uniformly convex Banach space, C be a nonempty closed convex subset of E. Let A be an α-inverse-strongly monotone mapping of C into E* satisfying ||Ay|| ≤ ||Ay - Au||, ∀y ∈ C and u ∈ VI(A, C) ≠ Ø. Let B : C → E* be a continuous and monotone mapping and f : C × C → ℝ be a bifunction satisfying the conditions (A 1) - (A 4), and φ : C → ℝ be a lower semi-continuous and convex function. Let T, S : C → C be a closed quasi-ϕ-nonexpansive mappings Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ GMEP(f, B,φ) ≠ ∅. Let {x n } be the sequence defined by x0 ∈ E and

where {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where  is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
-
(i)
lim infn→∞(1 - α n ) > 0;
-
(ii)
lim infn→∞(1 - β n ) > 0.
Then, the sequence {x n } converges strongly to ΠΩx0, where ΠΩ is generalized projection of E onto Ω
Proof. Since every closed quasi-ϕ-nonexpansive mapping is asymptotically quasi-ϕ-nonexpansive, the result is implied by Theorem 3.1.
Corollary 3.7. Let E be a uniformly smooth and 2-uniformly convex Banach space, C be a nonempty closed convex subset of E. Let A be an α-inverse-strongly monotone mapping of C into E* satisfying ||Ay|| ≤ ||Ay - Au||, ∀y ∈ C and u ∈ VI(A, C) ≠ Ø. Let B : C → E* be a continuous and monotone mapping and f : C × C → ℝ be a bifunction satisfying the conditions (A 1) - (A 4), and φ : C → ℝ be a lower semi-continuous and convex function. Let T, S : C → C be closed relatively nonexpansive mappings such that Ω := F(T) ∩ F(S) ∩ VI(A, C) ∩ GMEP(f, B,φ) ≠ Ø. Let {x n } be the sequence defined by x0 ∈ E and

where {α
n
} and {β
n
} are sequences in [0, 1], {λ
n
} ⊂ [a, b] for some a, b with 0 < a < b < c2α/2, where is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
is the 2-uniformly convexity constant of E and {r
n
} ⊂ [d, ∞) for some d > 0. Suppose that the following conditions are satisfied:
-
(i)
lim infn→∞(1 - α n ) > 0;
-
(ii)
lim infn→∞(1 - β n ) > 0.
Then, the sequence {x n } converges strongly to ΠΩx0, where ΠΩis generalized projection of E onto Ω.
Proof. Since every closed relatively nonexpansive mapping is quasi-ϕ-nonexpansive, the result is implied by Theorem 3.1.
Remark 3.8. Corollaries 3.7, 3.6 and 3.7 improve and extend the corresponding results of Saewan et al. [[51], Theorem 3.1] in the sense of changing the closed relatively quasi-nonexpansive mappings to be the more general than the closed and asymptotically quasi-ϕ-nonexpansive mappings and adjusting a problem from the classical equilibrium problem to be the generalized equilibrium problem.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Math Stud 1994, 63: 123–145.
Flores-Bazan F: Existence theory for finite-dimensional pseudomonotone equilibrium problems. Acta Appl Math 2003, 77: 249–297. 10.1023/A:1024971128483
Hadjisavvas N, Komlósi S, Schaible S: Handbook of Generalized Convexity and Generalized Monotonicity. Springer, Berlin; 2005.
Hadjisavvas N, Schaible S: From scalar to vector equilibrium problems in the quasimonotone case. J Optim Theory Appl 1998, 96: 297–309. 10.1023/A:1022666014055
Cai G, Hu CS: A hybrid approximation method for equilibrium and fixed point problems for a family of infinitely nonexpansive mappings and a monotone mapping. Nonlinear Anal.: Hybrid Syst 2009, 3: 395–407. 10.1016/j.nahs.2009.02.007
Ceng LC, Yao JC: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. J Comput Appl Math 2008, 214: 186–201. 10.1016/j.cam.2007.02.022
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. J Nonlinear Convex Anal 2005, 6: 117–136.
Flam SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Math Program 1997, 78: 29–41.
Jitpeera T, Kumam P: An extragradient type method for a system of equilibrium problems, variational inequality problems and fixed points of finitely many nonexpansive mappings. J Nonlinear Anal Optim.: Theory Appl 2010,1(1):71–91.
Jaiboon C, Kumam P, Humphries UW: An extra gradient method for relaxed cocoercive variational inequality and equilibrium problems. Anal Theory Appl 2009,25(4):381–400. 10.1007/s10496-009-0381-8
Kumam P: A Hybrid approximation method for equilibrium and fixed point problems for a monotone mapping and a nonexpansive mapping. Nonlinear Anal.: Hybrid Syst 2008,2(4):1245–1255. 10.1016/j.nahs.2008.09.017
Kumam P: A new hybrid iterative method for solution of equilibrium problems and fixed point problems for an inverse strongly monotone operator and a nonexpansive mapping. J Appl Math Comput 2009, 29: 263–280. 10.1007/s12190-008-0129-1
Kumam P, Petrot N, Wangkeeree R: A hybrid iterative scheme for equilibrium problems and fixed point problems of asymptotically k-strictly pseudo-contractions. J Comput Appl Math 2010, 233: 2013–2026. 10.1016/j.cam.2009.09.036
Petrot N, Wattanawitoon K, Kumam P: A hybrid projection method for generalized mixed equilibrium problems and fixed point problems in Banach spaces. Nonlinear Anal.: Hybrid Syst 2010, 4: 631–643. 10.1016/j.nahs.2010.03.008
Saewan S, Kumam P: Modified hybrid block iterative algorithm for convex feasibility problems and generalized equilibrium problems for uniformly quasi- ϕ -asymptotically nonexpansive mappings. Abstr Appl Anal 2010, 22. Article ID 357120
Saewan S, Kumam P: A hybrid iterative scheme for a maximal monotone operator and two countable families of relatively quasi-nonexpansive mappings for generalized mixed equilibrium and variational inequality problems. Abstr Appl Anal 2010, 31. Article ID 123027
Tada A, Takahashi W: Strong convergence theorem for an equilibrium problem and a nonexpansive mapping. In Nonlinear Analysis and Convex Analysis. Edited by: Takahashi W, Tanaka T. Yokohama Publishers, Yokohama; 2006:609–617.
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J Math Anal Appl 2007, 331: 506–515. 10.1016/j.jmaa.2006.08.036
Takahashi W, Zembayashi K: Strong convergence theorem by a new hybrid method for equilibrium problems and relatively nonexpansive mappings. Fixed Point Theory Appl 2008, 11. Article ID 528476
Wattanawitoon K, Kumam P, Humphries UW: Strong convergence theorem by the shrinking projection method for hemi-relatively nonexpansive mappings. Thai J Math 2009,7(2):329–337.
Ball K, Carlen EA, Lieb EH: Sharp uniform convexity and smoothness inequalities for trace norm. Invent Math 1994, 26: 137–150.
Takahashi Y, Hashimoto K, Kato M: On sharp uniform convexity, smoothness, and strong type, cotype inequalities. J Nonlinear Convex Anal 2002, 3: 267–281.
Rockafellar RT: On the maximality of sums of nonlinear monotone operators. Trans Am Math Soc 1970, 149: 75–88. 10.1090/S0002-9947-1970-0282272-5
Cho SY, Kang SM, Qin X: Weak and strong convergence of an implicit iteration process for two families of asymptotically nonexpansive mappings. Thai J Math 2010,8(3):521–533.
Katchang P, Kumam P: A new iterative algorithm of solution for equilibrium problems, variational inequalities and fixed point problems in a Hilbert space. J Appl Math Comput 2010, 32: 19–38. 10.1007/s12190-009-0230-0
Nakajo K, Shimoji K, Takahashi W: Strong convergence theorems of Halpern's type for families of nonexpansive mappings in Hilbert spaces. 2009,7(1):49–67.
Su Y, Shang M, Qin X: A general iterative scheme for nonexpansive mappings and inverse-strongly monotone mappings. J Appl Math Comput 2008, 28: 283–294. 10.1007/s12190-008-0103-y
Zhou H, Gao X: An iterative method of fixed points for closed and quasi-strict pseudo-contractions in Banach spaces. J Appl Math Comput 33(1–2):227–237.
Kirk WA: Metric fixed point theory: Old problems and new directions. Fixed Point Theory 2010,11(1):45–58.
Goebel K, Kirk WA: A fixed point theorem for asymptotically nonexpansive mappings. Proc Am Math Soc 1972, 35: 171–174. 10.1090/S0002-9939-1972-0298500-3
Alber Y: Metric and generalized projection operators in Banach spaces: properties and applications. In Theory and Applications of Nonlinear Operator of Accretive and Monotone Type. Edited by: Kartsatos AG. Marcel Dekker, New York; 1996:15–50.
Agarwal RP, Cho YJ, Qin X: Generalized projection algorithms for nonlinear operators. Numer Funct Anal Optim 2007, 28: 1197–1215. 10.1080/01630560701766627
Alber Y, Reich S: An iterative method for solving a class of nonlinear operator equations in Banach spaces. Panamer Math J 1994, 4: 39–54.
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Anal 1991, 16: 1127–1138. 10.1016/0362-546X(91)90200-K
Cioranescu I: Geometry of Banach Spaces, Duality Mappings and Nonlinear Problems. Kluwer, Dordrecht; 1990.
Takahashi W: Convex Analysis and Approximation Fixed points. Yokohama Publishers, Yokohama; 2000.
Reich S: A weak convergence theorem for the alternating method with Bregman distance. In Theory and Applications of Nonlinear Operators of Accretive and Monotone Type. Edited by: Kartsatos AG. Marcel Dekker, New York; 1996:313–318.
Butnariu D, Reich S, Zaslavski AJ: Asymptotic behavior of relatively nonexpansive operators in Banach spaces. J Appl Anal 2001, 7: 151–174. 10.1515/JAA.2001.151
Butnariu D, Reich S, Zaslavski AJ: Weak convergence of orbits of nonlinear operators in reflexive Banach spaces. Numer Funct Anal Optim 2003, 24: 489–508. 10.1081/NFA-120023869
Censor Y, Reich S: Iterations of para contractions and firmly nonexpansive operators with applications to feasibility and optimization. Optimization 1996, 37: 323–339. 10.1080/02331939608844225
Qin X, Su Y, Wu C, Liu K: Strong convergence theorems for nonlinear operators in Banach spaces. Commun Appl Nonlinear Anal 2007, 14: 35–50.
Qin X, Cho YJ, Kang SM: Convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces. J Comput Appl Math 2009, 225: 20–30. 10.1016/j.cam.2008.06.011
Zhou H, Gao G, Tan B: Convergence theorems of a modified hybrid algorithm for a family of quasi- ϕ -asymptotically nonexpansive mappings. J Appl Math Comput 2010,32(2):453–464. 10.1007/s12190-009-0263-4
Matsushita S, Takahashi W: Weak and strong convergence theorems for relatively nonexpansive mappings in Banach spaces. Fixed Point Theory Appl 2004, 1: 37–47.
Iiduka H, Takahashi W: Weak convergence of a projection algorithm for variational inequalities in a Banach space. J Math Anal Appl 2008, 339: 668–679. 10.1016/j.jmaa.2007.07.019
Takahashi W, Takeuchi Y, Kubota R: Strong convergence theorems by hybrid methods for families of nonexpansive mapping in Hilbert spaces. J Math Anal Appl 2008, 341: 276–286. 10.1016/j.jmaa.2007.09.062
Jaiboon C, Kumam P: Strong convergence theorems for solving equilibrium problems and fixed point problems of ξ-strict pseudo-contraction mappings by two hybrid projection methods. J Comput Appl Math 2010, 234: 722–732. 10.1016/j.cam.2010.01.012
Wattanawitoon K, Kumam P: Strong convergence theorem by a new hybrid algorithm for fixed point problems and equilibrium problems of two relatively quasi-nonexpansive mappings. Nonlinear Anal.: Hybrid Syst 2009,3(1):11–20. Corrigendum: Nonlinear Anal.: Hybrid Syst. 3(2), 176 (2009) 10.1016/j.nahs.2008.10.002
Kamraksa U, Wangkeeree R: A new hybrid method for solving generalized equilibrium problem and common fixed point in Banach spaces. J Nonlinear Anal Optim.: Theory Appl 2010,1(1):55–69.
Kumam P, Wattanawitoon K: Convergence theorems of a hybrid algorithm for equilibrium problems. Nonlinear Anal.: Hybrid Syst 2009, 3: 386–394. 10.1016/j.nahs.2009.02.006
Saewan S, Kumam P, Wattanawitoon K: Convergence theorem based on a new hybrid projection method for finding a common solution of generalized equilibrium and variational inequality problems in Banach spaces. Abstr Appl Anal 2010, 26. Article ID 734126
Plubtieng S, Thammathiwat T: Shrinking projection methods for a family of relatively nonexpansive mappings, equilibrium problems and variational inequality problems in Banach spaces. J Nonlinear Anal Optim.: Theory Appl 2010,1(1):97–110.
Markshoe P, Wangkeeree R, Kamraksa U: The shrinking projection method for generalized mixed equilibrium problems and fixed point problems in Banach spaces. J Nonlinear Anal Optim.: Theory Appl 2010,1(1):111–129.
Cholamjiak P, Suantai S: Convergence analysis for a system of equilibrium problems and a countable family of relatively quasi-nonexpansive mappings in Banach spaces. Abstr Appl Anal 2010, 17. Article ID 141376
Liu M, Chang S-S, Zuo P: Shrinking projection method of common solutions for generalized equilibrium quasi- ϕ -nonexpansive mapping and relatively nonexpansive mapping. J Inequal Appl 15. Article ID 101690
Wangkeeree R, Wangkeeree R: The shrinking projection method for solving variational inequality problems and fixed point problems in banach spaces. Abstr Appl Anal 2009, 26. Article ID 624798
Kang J, Su Y, Zhang X: Shrinking projection algorithm for fixed points of firmly nonexpansive mappings and its applications. Fixed Point Theory 2010,11(2):301–310.
Qin X, Cho SY, Kang SM: On hybrid projection methods for asymptotically quasi- ϕ -nonexpansive mappings. Appl Math Comput 2010, 215: 3874–3883. 10.1016/j.amc.2009.11.031
Chang S-S, Joseph Lee HW, Chan CK: A new hybrid method for solving generalized equilibrium problem variational inequality and common fixed point in Banach spaces with applications. Nonlinear Anal 2010, 73: 2260–2270. 10.1016/j.na.2010.06.006
Kim JK: Strong convergence theorem by hybrid projection methods for equilibriums problems and fixed point problems of the asymptotically quasi- ϕ -nonexpansive mappings. Fixed Point Theory Appl 2011, 1–20. Article ID 901256
Kamimura S, Takahashi W: Strong convergence of a proximal-type algorithm in a Banach space. SIAM J Optim 2002, 13: 938–945. 10.1137/S105262340139611X
Beauzamy B: Introduction to Banach Spaces and their Geometry. Noth Holland, Amsterdam 2nd edition. 1985.
Cho YJ, Zhou H, Guo G: Weak and strong convergence theorems for three-step iterations with errors for asymptotically nonexpansive mappings. Comput Math Appl 2004, 47: 707–717. 10.1016/S0898-1221(04)90058-2
Kohsaka F, Takahashi W: Strong convergence of an iterative sequence for maximal monotone operators in a Banach space. Abstr Appl Anal 2004, (3):239–249.
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively nonexpansive mappings in Banach spaces. Nonlinear Anal 2009, 70: 45–57. 10.1016/j.na.2007.11.031
Zhang S: Generalized mixed equilibrium problem in Banach spaces. Appl Math Mech English Edition 2009, 30: 1105–1112. 10.1007/s10483-009-0904-6
Acknowledgements
The authors would like to thank Prof. Jong Kyu Kim and the anonymous referees for their respective helpful discussions and suggestions in preparation of this article. This research was supported by grant under the program Strategic Scholarships for Frontier Research Network for the Joint Ph.D. Program of Thai Doctoral degree from the Office of the Higher Education Commission, Thailand. Moreover, the first author was also supported by the King Mongkuts Daimond scholarship for Ph.D. program at King Mongkuts University of Technology Thonburi (KMUTT), under project NRU-CSEC no.54000267, and the second author was supported by the Higher Education Commission and the Thailand Research Fund under Grant MRG5380044. Furthermore, this work was partially supported by the Higher Education Research Promotion and National Research University Project of Thailand, Office of the Higher Education Commission.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
SS designed and performed all the steps of proof in this research and also wrote the paper. PK participated in the design of the study and suggest many good ideas that made this paper possible and helped to draft the first manuscript. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saewan, S., Kumam, P. The shrinking projection method for solving generalized equilibrium problems and common fixed points for asymptotically quasi-ϕ-nonexpansive mappings. Fixed Point Theory Appl 2011, 9 (2011). https://doi.org/10.1186/1687-1812-2011-9
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-9
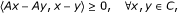
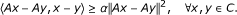
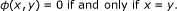
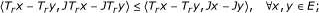
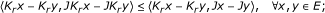
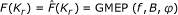 ;
;