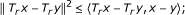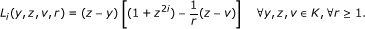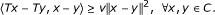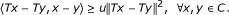- Research
- Open access
- Published:
Strong convergence theorems for equilibrium problems and fixed point problems: A new iterative method, some comments and applications
Fixed Point Theory and Applications volume 2011, Article number: 33 (2011)
Abstract
In this paper, we introduce a new approach method to find a common element in the intersection of the set of the solutions of a finite family of equilibrium problems and the set of fixed points of a nonexpansive mapping in a real Hilbert space. Under appropriate conditions, some strong convergence theorems are established. The results obtained in this paper are new, and a few examples illustrating these results are given. Finally, we point out that some 'so-called' mixed equilibrium problems and generalized equilibrium problems in the literature are still usual equilibrium problems.
2010 Mathematics Subject Classification: 47H09; 47H10, 47J25.
1 Introduction and preliminaries
Throughout this paper, we assume that H is a real Hilbert space with zero vector θ, whose inner product and norm are denoted by 〈·, ·〉 and || · ||, respectively. The symbols ℕ and ℝ are used to denote the sets of positive integers and real numbers, respectively. Let K be a nonempty closed convex subset of H and T : K → H be a mapping. In this paper, the set of fixed points of T is denoted by F(T). We use symbols → and ⇀ to denote strong and weak convergence, respectively.
For each point x ∈ H, there exists a unique nearest point in K, denoted by P K x, such that

The mapping P K is called the metric projection from H onto K. It is well known that P K satisfies

for every x, y ∈ H. Moreover, P K x is characterized by the properties: for x ∈ H, and z ∈ K,

Let f be a bi-function from K × K into ℝ. The classical equilibrium problem is to find x ∈ K such that

Let EP(f) denote the set of all solutions of the problem (1.1). Since several problems in physics, optimization, and economics reduce to find a solution of (1.1) (see, e.g., [1, 2]), some authors had proposed some methods to find the solution of equilibrium problem (1.1); for instance, see [1–4]. We know that a mapping S is said to be nonexpansive mapping if for all x, y ∈ K, ||Sx - Sy|| ≤ ||x - y||. Recently, some authors used iterative method including composite iterative, CQ iterative, viscosity iterative etc. to find a common element in the intersection of EP(f) and F(S); see, e.g., [5–11].
Let I be an index set. For each i ∈ I, let f i be a bi-function from K × K into ℝ. The system of equilibrium problem is to find x ∈ K such that

We know that  is the set of all solutions of the system of equilibrium problem (1.2).
is the set of all solutions of the system of equilibrium problem (1.2).
For each i ∈ I, if f i (x, y) = 〈A i x, y - x〉, where A i : K → K is a nonlinear operator, then the problem (1.2) becomes the following system of variational inequality problem:

It is obvious that the problem (1.3) is a special case of the problem (1.2).
The following Lemmas are crucial to our main results.
Lemma 1.1 (Demicloseness principle[12]) Let H be a real Hilbert space and K a closed convex subset of H. S : K → H is a nonexpansive mapping. Then the mapping I - S is demiclosed on K, where I is the identity mapping, i.e., x n ⇀ x in K and (I - S)x n → y implies that × ∈ K and (I - S)x = y.
Lemma 1.2[13] Let {x n }and {y n } be bounded sequences in a Banach space E and let {β n } be a sequence in [0,1] with 0 < lim infn→∞β n ≤ lim supn→∞β n < 1. Suppose xn+1= β n y n + (1 - β n )x n for all integers n ≥ 0 and lim supn→∞(||yn+1- y n || - ||xn+1- x n ||) ≤ 0, then limn→∞||y n - x n || = 0.
Lemma 1.3[5] Let H be a real Hilbert space. Then the following hold.
-
(a)
||x + y||2 ≤ ||y||2 + 2〈x, x + y〉 for all x, y ∈ H;
-
(b)
||αx + (1 - α)y||2 = α||x||2 + (1 - α) ||y||2 - α(1 - α) ||x - y||2 for all x, y ∈ H and α ∈ ℝ;
-
(c)
||x - y||2 = ||x||2 + ||y||2 - 2 〈x, y〉 for all x, y ∈ H.
Lemma 1.4. [14] Let {a n } be a sequence of nonnegative real numbers satisfying the following relation:

If
-
(i)
λ n ∈ [0,1],
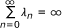 or, equivalently,
or, equivalently,  ;
; -
(ii)
 or
or 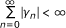 ,
,
then  .
.
Lemma 1.5[1] Let K be a nonempty closed convex subset of H and F be a bi-function of K × K into ℝ satisfying the following conditions.
(A1) F(x, x) = 0 for all × ∈ K;
(A2) F is monotone, that is, F(x, y) + F(y, x) ≤ 0 for all x, y ∈ K;
(A3) for each x, y, z ∈ K,

(A4) for each × ∈ K, y → F(x, y) is convex and lower semi-continuous.
Let r > 0 and × ∈ H. Then, there exists z ∈ K such that

Lemma 1.6[3] Let K be a nonempty closed convex subset of H and let F be a bi-function of K × K into R satisfying (A1) - (A4). For r > 0 and × ∈ H, define a mapping T r : H → K as follows:

for all × ∈ H. Then the following hold:
-
(i)
T r is single-valued;
-
(ii)
T r is firmly nonexpansive, that is, for any x, y ∈ H,
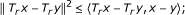
-
(iii)
F(T r ) = EP (F);
-
(iv)
EP(F) is closed and convex.
2 Main results and their applications
Let I = {1, 2,..., k} be a finite index set, where k ∈ ℕ. For each i ∈ I, let f
i
be a bi-functions from K × K into ℝ satisfying the conditions (A1)-(A4). Denote  by
by

For each (i, n) ∈ I × ℕ, applying Lemmas 1.5 and 1.6,  is a firmly nonexpansive single-valued mapping such that
is a firmly nonexpansive single-valued mapping such that  is closed and convex. For each i ∈ I, let
is closed and convex. For each i ∈ I, let  , n ∈ ℕ.
, n ∈ ℕ.
First, let us consider the following example.
Example A Let f
i
: [-1, 0]×[-1,0] → ℝ be defined by f
i
(x, y) = (1+x2i)(x - y), i = 1, 2, 3. It is easy to see that for any i ∈ {1, 2, 3}, f
i
(x, y) satisfies the conditions (A1)-(A4) and  . Let Sx = x3 and
. Let Sx = x3 and  , ∀ x ∈ [-1, 0] Then g is a
, ∀ x ∈ [-1, 0] Then g is a  -contraction from K into itself and S : K → K is a nonexpansive mapping with
-contraction from K into itself and S : K → K is a nonexpansive mapping with  . Let λ ∈ (0, 1), {r
n
} ⊂ [1, + ∞) and {α
n
} ⊂ (0,1) satisfy the conditions (i) limn→∞α
n
= 0, and (ii)
. Let λ ∈ (0, 1), {r
n
} ⊂ [1, + ∞) and {α
n
} ⊂ (0,1) satisfy the conditions (i) limn→∞α
n
= 0, and (ii)  , or equivalently,
, or equivalently,  ; e.g., let
; e.g., let  , {α
n
} ⊂ (0, 1) and {r
n
} ⊂ [1, + ∞) be given by
, {α
n
} ⊂ (0, 1) and {r
n
} ⊂ [1, + ∞) be given by

Define a sequence {x n } by

Then the sequences {x
n
} and  , i = 1, 2, 3, defined by (2.1) all strongly converge to 0.
, i = 1, 2, 3, defined by (2.1) all strongly converge to 0.
Proof
-
(a)
By Lemmas 1.5 and 1.6, (2.1) is well defined.
-
(b)
Let K = [-1, 0]. For each i ∈ {1, 2, 3}, define
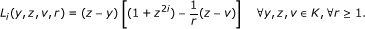
We claim that for each v ∈ K and any i ∈ {1, 2, 3}, there exists a unique z = 0 ∈ K such that

or, equivalently,

Obviously, z = 0 is a solution of the problem  . On the other hand, there does not exist z ∈ [-1, 0) such that z - y ≤ 0 and
. On the other hand, there does not exist z ∈ [-1, 0) such that z - y ≤ 0 and  . So z = 0 is the unique solution of the problem
. So z = 0 is the unique solution of the problem  .
.
-
(c)
We notice that (2.1) is equivalent with (2.2), where
 (2.2)
(2.2)
It is easy to see that {x
n
} ⊂ [-1, 0], so, by (b),  for all n ∈ ℕ. We need to prove x
n
→ 0 as n → ∞. Since z
n
= 0 for all n ∈ ℕ, we have y
n
= (1 -λ)x
n
and
for all n ∈ ℕ. We need to prove x
n
→ 0 as n → ∞. Since z
n
= 0 for all n ∈ ℕ, we have y
n
= (1 -λ)x
n
and

for all n ∈ ℕ. For any n ∈ ℕ, from (2.3), we have

Hence {|x
n
|} is a strictly deceasing sequence and |x
n
| ≥ 0 for all n ∈ ℕ. So  exists.
exists.
On the other hand, for any n, m ∈ ℕ with n > m, using (2.4), we obtain

which implies  . Therefore {x
n
} strongly converges to 0. □
. Therefore {x
n
} strongly converges to 0. □
In this paper, motivated by the preceding Example A, we introduce a new iterative algorithm for the problem of finding a common element in the set of solutions to the system of equilibrium problem and the set of fixed points of a nonexpansive mapping. The following new strong convergence theorem is established in the framework of a real Hilbert space H.
Theorem 2.1 Let K be a nonempty closed convex subset of a real Hilbert space H and I = {1, 2,..., k} be a finite index set. For each i ∈ I, let f
i
be a bi-function from K × K into ℝ satisfying (A1)-(A4). Let S : K → K be a nonexpansive mapping with  . Let λ, ρ ∈ (0, 1) and g : K → K is a ρ-contraction. Let {x
n
} be a sequence generated in the following manner:
. Let λ, ρ ∈ (0, 1) and g : K → K is a ρ-contraction. Let {x
n
} be a sequence generated in the following manner:

If the above control coefficient sequences {α n } ⊂ (0, 1) and {r n } ⊂ (0, +∞) satisfy the following restrictions:
(D1)  ,
,  and
and  ;
;
(D2)  and
and .
.
then the sequences {x
n
} and , for all i ∈ I, converge strongly to an element c = PΩg(c) ∈ Ω. The following conclusion is immediately drawn from Theorem 2.1.
, for all i ∈ I, converge strongly to an element c = PΩg(c) ∈ Ω. The following conclusion is immediately drawn from Theorem 2.1.
Corollary 2.1 Let K be a nonempty closed convex subset of a real Hilbert space H. Let f be a bi-function from K × K into ℝ satisfying (A1)-(A4) and S : K → K be a nonexpansive mapping with Ω = EP(f) ∩F(S) ≠ ∅. Let λ, ρ ∈ (0,1) and g : K → K is a ρ-contraction. Let {x n } be a sequence generated in the following manner:

If the above control coefficient sequences {α n } ⊂ (0, 1) and {r n } ⊂ (0, +∞) satisfy all the restrictions in Theorem 2.1, then the sequences {x n } and {u n } converge strongly to an element c = PΩg(c) ∈ Ω, respectively.
If f
i
(x, y) ≡ 0 for all (x, y) ∈ K × K in Theorem 2.1 and all i ∈ I, then, from the algorithm (D
H
), we obtain  , ∀ i ∈ I. So we have the following result.
, ∀ i ∈ I. So we have the following result.
Corollary 2.2 Let K be a nonempty closed convex subset of a real Hilbert space H. Let S : K → K be a nonexpansive mapping with F(S) ≠ ∅. Let λ, ρ ∈ (0, 1) and g : K → K is a ρ-contraction. Let {x n } be a sequence generated in the following manner:

If the above control coefficient sequences {α
n
} ⊂ (0, 1) satisfy ,
,  and
and , then the sequences {x
n
} converge strongly to an element c = PΩg(c) ∈ F (S).
, then the sequences {x
n
} converge strongly to an element c = PΩg(c) ∈ F (S).
As some interesting and important applications of Theorem 2.1 for optimization problems and fixed point problems, we have the following.
Application (I) of Theorem 2.1 We will give an iterative algorithm for the following optimization problem with a nonempty common solution set:

where h i (x), i ∈ {1, 2,..., k}, are convex and lower semi-continuous functions defined on a closed convex subset K of a Hilbert space H (for example, h i (x) = xi , x ∈ K := [0, 1], i ∈ {1, 2,..., k}).
If we put f
i
(x, y) = h
i
(y) - h
i
(x), i ∈ {1, 2,..., k}, then  is the common solution set of the problem (OP), where
is the common solution set of the problem (OP), where  denote the common solution set of the following equilibrium:
denote the common solution set of the following equilibrium:

For i ∈ {1, 2,..., k}, it is obvious that the f i (x, y) satisfies the conditions (A1)-(A4). Let S = I (identity mapping), then from (D H ), we have the following algorithm

where x1 ∈ K, λ ∈ (0, 1), g : K → K is a ρ-contraction. From Theorem 2.1, we know that {x
n
} and  , i ∈{1,2,..., k}, generated by (2.5), strongly converge to an element of
, i ∈{1,2,..., k}, generated by (2.5), strongly converge to an element of  if the coefficients {α
n
} and {r
n
} satisfy the conditions of Theorem 2.1.
if the coefficients {α
n
} and {r
n
} satisfy the conditions of Theorem 2.1.
Application (II) of Theorem 2.1 Let H, K, I, λ, ρ, g be the same as Theorem 2.1. Let A1, A2,..., A
k
: K → K be k nonlinear mappings with  . For any i ∈ I, put f
i
(x, y) = 〈x - A
i
x, y - x〉, ∀ x, y ∈ K. Since
. For any i ∈ I, put f
i
(x, y) = 〈x - A
i
x, y - x〉, ∀ x, y ∈ K. Since  , we have
, we have  . Let S = I (identity mapping) in the algorithm (D
H
). Then the sequences {x
n
} and
. Let S = I (identity mapping) in the algorithm (D
H
). Then the sequences {x
n
} and  , defined by the algorithm (D
H
), converge strongly to a common fixed point of {A1, A2,..., A
k
}, respectively.
, defined by the algorithm (D
H
), converge strongly to a common fixed point of {A1, A2,..., A
k
}, respectively.
The following result is important in this paper.
Lemma 2.1 Let H be a real Hilbert space. Then for any x1, x2,... x
k
∈ H and a1, a2,..., a
k
∈ [0,1] with , k ∈ ℕ, we have
, k ∈ ℕ, we have

Proof It is obvious that (2.6) is true if a j = 1 for some j, so it suffices to show that (2.6) is true for a j ≠ 1 for all j. The proof is by mathematic induction on k. Clearly, (2.6) is true for k = 1. Let x1, x2 ∈ H and a1, a2 ∈ [0,1] with a1 + a2 = 1. By Lemma 1.3, we obtain

which means that (2.6) hold for k = 2. Suppose that (2.6) is true for k = l ∈ ℕ. Let x1, x2,..., x
l
, xl+1∈ H and a1, a2,..., a
l
, al+1∈ [0, 1) with  . Let
. Let  . Then applying the induction hypothesis we have
. Then applying the induction hypothesis we have

Hence, the equality (2.6) is also true for k = l + 1. This completes the induction. □
3 Proof of Theorem 2.1
We will proceed with the following steps.
Step 1: There exists a unique c ∈ Ω ⊂ H such that PΩg(c) = c.
Since PΩg is a ρ-contraction on H, Banach contraction principle ensures that there exists a unique c ∈ H such that c = PΩg(c) ∈ Ω.
Step 2: We prove that the sequences {x
n
}, {y
n
}, {z
n
} and  , ∀i ∈ I, are all bounded.
, ∀i ∈ I, are all bounded.
First, we notice that (D H ) is equivalent with (Z H ), where

For each i ∈ I, we have

For any n ∈ ℕ, from (Z H ) we have

and

Since g is a ρ-contraction, it follows from (3.2) that

By induction, we obtain

which shows that {x
n
} is bounded. Also, we know that {y
n
}, {z
n
} and  , ∀i ∈ I, are all
, ∀i ∈ I, are all
bounded.
Step 3: We prove limn→∞||xn+1- x n || = 0.
For each i ∈ I, since  ,
,  , from (Z
H
), we have
, from (Z
H
), we have

and

By (3.3) and (3.4) and (A2),

which implies

It follows from (3.5) that

Let  . For any n ∈ ℕ, since
. For any n ∈ ℕ, since  , by (3.6), we have
, by (3.6), we have

Set

where β n = 1 - (1 - λ)(1 - α n ), n ∈ ℕ. Then for each n ∈ ℕ,

and

For any n ∈ ℕ, since

by (3.7), it follows that

From this and (D1), (D2), we get

By Lemma 1.2 and (3.11),

Owing to (3.9) and (3.12), we obtain

Step 4: We show  .
.
By (3.6), (3.13) and (D2), we have

From (Z H ), we get

Since ||x n - y n || ≤ ||x n - xn+1|| + ||xn+1- y n ||, by (3.13) and (3.14),

which implies that

By Lemma 1.6,

which yields that

From (3.15) and Lemma 2.1,

Since

where

We have

Letting n → ∞ in the inequality (3.16), we obtain

Furthermore, it is easy to prove that

For any i ∈ I, since

it implies

Step 5: Prove lim supn→∞〈g(c) - q, x n - c〉 ≤ 0.
Take a subsequence  of {x
n
} such that
of {x
n
} such that

Since  is bounded, there exists a subsequence of
is bounded, there exists a subsequence of  which is still denoted by
which is still denoted by  such that
such that  as ℓ → ∞. Notice that for each i ∈ I,
as ℓ → ∞. Notice that for each i ∈ I,  by (3.17), so we also have
by (3.17), so we also have  as ℓ → ∞, ∀ i ∈ I.
as ℓ → ∞, ∀ i ∈ I.
We want to show z ∈ Ω. First, we show that z ∈ F(S). In fact, since  and
and  as ℓ → ∞, by Lemma 1.1, we have (I - S)z = θ or, equivalently, z ∈ F(S).
as ℓ → ∞, by Lemma 1.1, we have (I - S)z = θ or, equivalently, z ∈ F(S).
For each i ∈ I, since  , ∀ y ∈ K, it follows from (A2) that
, ∀ y ∈ K, it follows from (A2) that

and hence

Applying (3.17) and (A4),

Let y ∈ K be given. Put y t = ty + (1 - t)z, t ∈ (0, 1). Then y t ∈ K and f i (y t , z) ≤ 0 for all i ∈ I. By (A1) and (A4), we get

For any i ∈ I, by (A3), we have

Hence, from (3.21),  . Therefore, we proved
. Therefore, we proved  . On the other hand, by (3.19), we obtain
. On the other hand, by (3.19), we obtain

Step 6: Finally, we prove {x
n
} and  , for all i ∈ I, converge strongly to c = PΩg(c) ∈ Ω.
, for all i ∈ I, converge strongly to c = PΩg(c) ∈ Ω.
From (Z H ) and (a) of Lemma 1.3, we have

For any n ∈ ℤ, let

and

From (3.23), we have

It is easy to verify that all conditions of Lemma 1.4 are satisfied. Hence, applying Lemma 1.4, we obtain limn→∞a n = 0 which implies

or equivalence, {x
n
} strongly converges to c. By (3.17), we can prove that for any i ∈ I,  strongly converges to c. The proof of Theorem 2.1 is completed. □
strongly converges to c. The proof of Theorem 2.1 is completed. □
4 Further remarks
Let K be a nonempty closed convex subset of H and f be a bi-function of K × K into ℝ.
Remark 4.1 Recently, some authors introduced the following mixed equilibrium problem (MEP, for short) (see [15–17] and references therein) and generalized equilibrium problem (GEP, for short) (see [18–20] and references therein):
where φ : C → ℝ is a real-valued function.
where A : C → H is a nonlinear operator.
In [15–17], the authors gave some iterative methods for finding the solution of MEP when the bi-function f(x, y) admits the conditions (A1)-(A4) and the real-valued function φ satisfies the following condition:
(A5) φ : C → ℝ is a proper lower semi-continuous and convex function.
However, in this case, we argue that the problem MEP is still the equilibrium problem (1.1). In fact, if we put f1(x, y) = f(x, y), f2(x, y) = φ(y) - φ(x) and F(x, y) = f1(x, y) + f2(x, y) for each (x, y) ∈ C × C, then f1(x, y) satisfies the conditions (A1)-(A4), f2(x, y) satisfies the condition (A5) and the function φ must satisfy the conditions (A1)-(A4). This shows that for each (x, y) ∈ C × C, F(x, y) satisfies the conditions (A1)-(A4). So, when we study the solution of MEP, we only need to study the solution of the equilibrium (1.1). This also shows that some "so-called" mixed equilibrium problem studied in [15–17] is still the equilibrium problem (1.1).
Remark 4. 2 Let us recall some well-known definitions. A mapping T : C → C is said to be
-
(1)
v-expansive if ||Tx - Ty|| ≥ v||x - y|| for all x, y ∈ C. In particular, if v = 1, then T is called expansive.
-
(2)
v-strongly monotone if there exists a constant v > 0 such that
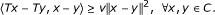
Clearly, any v-strongly monotone mapping is v-expansive.
-
(3)
u-inverse strongly monotone if there exists a constant u > 0 such that
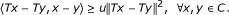
-
(4)
L-Lipschitz continuous if ||Tx - Ty|| ≤ L||x - y|| for all x, y ∈ C. In particular, if L = 1, then T is called nonexpansive.
It is easy to see that a u-inverse strongly monotone operator is  -Lipschitz continuous.
-Lipschitz continuous.
For the problem GEP, if the nonlinear operator A : C → H is a u-inverse strongly monotone operator and the bi-function f(x, y) admits the conditions (A1)-(A4), we argue that the problem GEP is still the problem (1.1) and so it is indeed not a generalization. In fact, if A is a u-inverse strongly monotone operator from C into H, then A is a continuous operator. So, we obtain easily that the function (x, y) → <Ax, y - x〉, ∀x, y ∈ C, satisfies the conditions (A1)-(A4). Hence, if we put F(x, y) = f(x, y) + 〈Ax, y - x〉 ≥ 0, then the problem GEP studied in [18–20] is still the problem (1.1).
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Math Stud 1994, 63: 123–145.
Moudafi A, Théra M: Proximal and Dynamical Approaches to Equilibrium Problems. In Lecture Notes in Economics and Mathematical Systems. Volume 477. Springer, Heidelberg; 1999:187–201.
Combettes PL, Hirstoaga A: Equilibrium programming in Hilbert spaces. J Nonlinear Convex Anal 2005, 6: 117–136.
Flam SD, Antipin AS: Equilibrium progamming using proximal-link algorithms. Math Program 1997, 78: 29–41.
Chang SS, Joseph Lee HW, Chan CK: A new method for solving equilibrium problem fixed point problem and variational inequality problem with application to optimization. Nonlinear Anal 2009, 70: 3307–3319. 10.1016/j.na.2008.04.035
Jung JS: Strong convergence of composite iterative methods for equilibrium problems and fixed point problems. Appl Math Comput 2009, 213: 498–505. 10.1016/j.amc.2009.03.048
Kumam P: A hybrid approximation method for equilibrium and fixed point problems for a monotone mapping and a nonexpansive mapping. Nonlinear Anal Hybrid Sys 2008, 2: 1245–1255. 10.1016/j.nahs.2008.09.017
Su YF, Shang MJ, Qin XL: An iterative method of solution for equilibrium and optimization problems. Nonlinear Anal 2008, 69: 2709–2719. 10.1016/j.na.2007.08.045
Tada A, Takahashi W: Weak and strong convergence theorems for a nonexpansive mapping and an equilibrium problem. J Optim Theory Appl 2007, 133: 359–370. 10.1007/s10957-007-9187-z
Takahashi S, Takahashi W: Viscosity approximation methods for equilibrium problems and fixed point problems in Hilbert spaces. J Math Anal Appl 2007, 331: 506–515. 10.1016/j.jmaa.2006.08.036
Wang S, Hu C, Chai G: Strong convergence of a new composite iterative method for equilibrium problems and fixed point problems. Appl Math Comput 2010, 215: 3891–3898. 10.1016/j.amc.2009.11.036
Goebel K, Kirk WA: Topics in metric fixed point theory. In Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge; 1990.
Suzuki T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. J Fixed Point Theory Appl 2005,2005(1):103–123. 10.1155/FPTA.2005.103
Xu HK: An iterative approach to quadratic optimization. J Optim Theory Appl 2003, 116: 659–678. 10.1023/A:1023073621589
Katchang P, Jitpeera T, Kumam P: Strong convergence theorems for solving generalized mixed equilibrium problems and general system of variational inequalities by the hybrid method. Nonlinear Anal Hybrid Sys 2010, 4: 838–852. 10.1016/j.nahs.2010.07.001
Jaiboon C, Kumam P: A general iterative method for addressing mixed equilibrium problems and optimization problems. Nonlinear Anal 2010, 72: 1180–1202.
Imnang S, Suantai S: Strong convergence theorems for a general system of variational inequality problems, mixed equilibrium problems and fixed points problems with applications. Math Comput Model 2010, 9–10: 1682–1696.
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Anal 2008, 69: 1025–1033. 10.1016/j.na.2008.02.042
Cho YJ, Qin X, Kang JI: Convergence theorems based on hybrid methods for generalized equilibrium problems and fixed point problems. Nonlinear Anal 2009, 71: 4203–4214. 10.1016/j.na.2009.02.106
Qin X, Cho YJ, Kang SM: Viscosity approximation methods for generalized equilibrium problems and fixed point problems with applications. Nonlinear Anal 2010, 72: 99–112. 10.1016/j.na.2009.06.042
Colao V, Acedo GL, Marino G: An implicit method for finding common solutions of variational inequalities and systems of equilibrium problems and fixed points of infinite family of nonexpansive mappings. Nonlinear Anal 2009, 71: 2708–2715. 10.1016/j.na.2009.01.115
Kangtunyakarn A, Suantai S: A new mapping for finding common solutions of equilibrium problems and fixed point problems of finite family of nonexpansive mappings. Nonlinear Anal 2009, 71: 4448–4460. 10.1016/j.na.2009.03.003
Ceng L-C, Al-Homidan S, Ansari QH, Yao J-C: An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings. J Comput Appl Math 2009, 2: 967–974.
Jaiboon C, Kumam P: Strong convergence theorems for solving equilibrium problems and fixed point problems of ξ-strict pseudo-contraction mappings by two hybrid projection methods. J Comput Appl Math 2010, 3: 722–732.
Acknowledgements
Zhenhua He was supported by the Natural Science Foundation of Yunnan Province (2010ZC152) and the Scientific Research Foundation from Yunnan Province Education Committee (08Y0338); Wei-Shih Du was supported by the National Science Council of the Republic of China.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
Both authors contributed equally and significantly in writing this paper. Both authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
He, Z., Du, WS. Strong convergence theorems for equilibrium problems and fixed point problems: A new iterative method, some comments and applications. Fixed Point Theory Appl 2011, 33 (2011). https://doi.org/10.1186/1687-1812-2011-33
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-33
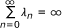 or, equivalently,
or, equivalently,  ;
; or
or 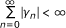 ,
,