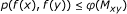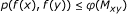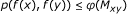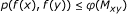- Research
- Open access
- Published:
Generalization of fixed point theorems in ordered metric spaces concerning generalized distance
Fixed Point Theory and Applications volume 2011, Article number: 30 (2011)
Abstract
In this article, we consider ordered metric spaces concerning generalized distance and prove some fixed point theorems in these spaces. Our results generalize, improve, and simplify the proof of the previous results given by some authors.
Mathematics Subject Classification (2000)
47H10, 54H25
1. Introduction and Preliminary
Recently, Nieto and Rodriguez-Lopez [1, 2], Ran and Reurins [3], Petrusel and Rus [4] presented some new results in partially ordered metric spaces. Their main idea was to combine the ideas of iterative technique in the contractive mapping with these in monotone technique.
Recently, Kada et al. [5, 6] in 1996 introduced the concept of w-distance in a metric space and prove some fixed point theorems. For the study of fixed point theorem concerning generalized distance followed in other articles, see [5, 7–15].
The aim of this article is to use the concept of w-distance to generalize the fixed point theorems in partially ordered metric spaces. Our results not only generalize some fixed point theorems, but also improve and simplify the previous results.
In the sequel, we state some definitions and a lemma which we will use in our main results.
Definition 1.1. ([5, 8, 10]) Let (X, d) be a metric space. Then, a function p : X × X → [0, ∞) is called a w-distance on X if the following conditions are satisfied:
-
(a)
p(x, z) ≤ p(x, y) + p(y, z) for any x, y, z ∈ X;
-
(b)
for any x ∈ X, p(x, .) : X → [0, ∞) is lower semi-continuous;
-
(c)
for any ε > 0, there exists δ > 0 such that p(x, z) ≤ δ and p(z, y) ≤ δ imply d(x, y) ≤ ε.
We know that a real-valued function f defined in a metric space X is said to be lower semi-continuous at a point x0 ∈ X if either  or
or  , whenever x
n
∈ X for each n ∈ N and x
n
→ x0.
, whenever x
n
∈ X for each n ∈ N and x
n
→ x0.
Lemma 1.2. ([5, 7]) Let (X, d) be a metric space and p be a w-distance on X. Let {x n }, {y n } be sequences in X, {α n }, {β n } be sequences in [0, ∞) converging to zero and let x, y, z ∈ X. Then, the following conditions hold:
-
(1)
If p(x n , y) ≤ α n and p(x n , z) ≤ β n for any n ∈ N, then y = z. In particular, if p(x.y) = 0 and p(x, z) = 0, then y = z;
-
(2)
If p(x n , y n ) ≤ α n and p(x n , z) ≤ β n for any n ∈ N, then d(y n , z) → 0;
-
(3)
If p(x n , x m ) ≤ α n for any n, m ∈ N with m > n, then {x n } is a Cauchy sequence;
-
(4)
If p(y, x n ) ≤ α n for any n ∈ N, then {x n } is a Cauchy sequence.
Let f : X → X be an operator:
-
(1)
I(f) is the set of all nonempty invariant subsets of f, i.e., I(f) = {Y ⊂ X : f(Y ) ⊂ Y } and F f = {x ∈ X : x = f(x)}.
-
(2)
The operator f is called Picard operator (briefly, PO) if there exists x* ∈ X such that F f = {x*} and, for all x ∈ X, {fn (x)} converges to x*.
-
(3)
The operator f is called orbitally U-continuous for any U ⊂ X × X if the following condition holds:
For any x ∈ X,  as i → ∞ and
as i → ∞ and  for any i ∈ N imply that
for any i ∈ N imply that  as i → ∞.
as i → ∞.
-
(4)
Let (X, ≤) be a partially ordered set. Then,

and [x, y]≤ = {z ∈ X : x ≤ z ≤ y}, where x, y ∈ X and x ≤ y.
-
(5)
If g : Y → Y is an operator, then the Cartesian product of f and g is the mapping f × g : X × Y → X × Y defined by (f × g)(x, y) = (f(x), g(y)) for all (x, y) ∈ X × Y.
-
(6)
φ : R + → R + is said to be a comparison function if it is increasing and φn (t) → 0 as n → ∞. As a consequence, we also have φ (t) < t for any t > 0, φ (0) = 0, and φ is right continuous at 0.
2. Main Results
Now, we give the main results of this article.
Theorem 2.1. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator. Let p be a w-distance on (X, d) and suppose that
-
(a)
X ≤ ∈ I(f × f );
-
(b)
there exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;
-
(c)
(c 1) f is orbitally continuous or
(c2) f is orbitally X≤-continuous and there exists a subsequence of {f n (x0)} such that
of {f n (x0)} such that for any k ∈ N ;
for any k ∈ N ;
-
(d)
there exists a comparison function φ : R + → R + such that

for all (x, y) ∈ X≤, where

-
(e)
the metric d is complete.
Then F f ≠ ∅.
Proof. If f(x0) = x0, then the proof is completed. Let x0 ∈ X be such that (x0, f (x0)) ∈ X≤. By (a), since (f × f )(X≤) ⊂ X≤, we have (f × f )(x0, f (x o )) ∈ X≤ and so (f(x0), f2(x o )) ∈ X≤.
Continuing this process, we obtain

for any n ∈ N.
Now, we show that

for any n ∈ N. Let p0 = p(x0, f (x0)) and p n = p(f n (x0), fn+1(x0)) for any n ∈ N. Then we have

for any n ∈ N. If max{pn-1, p n } = pn-1, then (3.1) follows. Otherwise, max{pn-1, p n } = p n Then, by (3.2), we have p n ≤ φ(p n ) ≤ p n and so p n = 0 and (3.1) follows. By induction, we obtain

or, equivalently,

for any n ∈ N, Now, we have

as n → ∞.
Similarly, we have

as n → ∞ and so, by induction, we obtain

as n → ∞ for any k > 0. Therefore, {fn (x0)} is a Cauchy sequence in X. Since X is complete, there exists x* ∈ X such that fn (x0) → x* as n → ∞.
Now, we show that x* is a fixed point. If (c1) holds, then fn+1(x0) → f (x*) and, by lower semi-continuity of p(fn (x0), ·), we have


and α n , β n → 0 as n → ∞. Thus, by (3.3) and Lemma 1.2, we conclude that f (x*) = x*.
Now, suppose that (c2) holds. Since  converges to x* and f is X≤-orbitally continuous, it follows that
converges to x* and f is X≤-orbitally continuous, it follows that  converges to f (x*). Similarly, by lower semi-continuity of p(fn (x0), ·), we conclude that f (x*) = x*. This completes the proof. □
converges to f (x*). Similarly, by lower semi-continuity of p(fn (x0), ·), we conclude that f (x*) = x*. This completes the proof. □
Corollary 2.2. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.
Let p be a w-distance on (X, d) and suppose that
-
(a)
X ≤ ∈ I(f × f );
-
(b)
there exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;
-
(c)
(c 1)) f is orbitally continuous or
(c2) f is orbitally X≤-continuous and there exists a subsequence of {fn (x0)} such that
of {fn (x0)} such that for any k ∈ N ;
for any k ∈ N ;
-
(d)
and there is a comparison function φ : R + → R + such that

for any (x, y) ∈ X≤, where

-
(e)
the metric d is complete;
-
(f)
if (x, y) ∈ X ≤ and (y, z) ∈ X ≤ .vskip 1 mm
Then, F f ≠ ∅.
Theorem 2.3. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.
Let p be a w-distance on (X, d) and suppose that
-
(a)
X ≤ ∈ I(f × f );
-
(b)
There exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;
-
(c)
(c 1) f is orbitally continuous or
(c2) f is orbitally X≤-continuous and there exists a subsequence of {fn(x0)} such that
of {fn(x0)} such that for any k ∈ N ;
for any k ∈ N ;
-
(d)
there is a comparison function φ : R + → R + such that
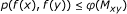
for any (x, y) ∈ X≤, where

-
(e)
the metric d is complete;
-
(f)
if x, y ∈ X with (x, y) ∉ X ≤, then there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ . .
Then, f is PO.
Proof. According to Theorem 2.1, there exists x* ∈ X such that f(x*) = x*. Take x ∈ X.
If (x, x0) ∈ X≤, then (f n (x), f n (x 0)) ∈ X≤ and so

for any n ∈ N. Thus, by Lemma 1.2, fn (x) → x* as n → ∞.
If (x, x0) ∉ X≤, then there exists z ∈ X such that (x, z) ∈ X≤ and (x0, z) ∈ X≤ and so

for any n ∈ N. Thus, by Lemma 1.2, we have fn (z) → x* as n → ∞. Also, since (x, z) ∈ X≤, we have f n (z) → x* as n → ∞. Consequently, f n (x) → x* as n → ∞.
Now, if there exist y ∈ X such that f(y) = y, then

and so, by Lemma 2.1, y = x*, i.e., F f = {x*}. This completes the proof. □
Corollary 2.4. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.
Let p be a w-distance on (X, d) and suppose that
-
(a)
if x, y ∈ X with (x, y)X ≤ there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ ;
-
(b)
X ≤ ∈ I(f × f ) ;
-
(c)
There exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;
-
(d)
(d 1) f is orbitally continuous or
(d2) f is orbitally X≤-continuous and there exists a subsequence of {fn (x0)} such that
of {fn (x0)} such that for any k ∈ N ;
for any k ∈ N ;
-
(e)
there is a comparison function φ : R + → R + such that
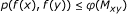
for any (x, y) ∈ X≤, where

-
(f)
the metric d is complete,
Then, f is PO.
Corollary 2.5. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.
Let p be a w-distance on (X, d) and suppose that
-
(a)
if x, y ∈ X with (x, y)X ≤, then there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ ;
-
(b)
if (x, y) ∈ X ≤ and (y, z) ∈ X ≤, then (x, z) ∈ X ≤ ;
-
(c)
f is orbitally continuous (iv) there is a comparison function φ : R + → R + such that
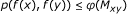
for any (x, y) ∈ X≤, where

-
(d)
the metric d is complete,
Then, f is PO.
Corollary 2.6. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.
Let p be a w-distance on (X, d) and suppose that
-
(a)
if x, y ∈ X with (x, y)X ≤, then there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ ;
-
(b)
X ≤ ∈I(f × f ) ;
-
(c)
there exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;
-
(d)
if (x, y) ∈ X ≤ and (y, z) ∈ X ≤, then (x, z) ∈ X ≤ ;
-
(e)
(e 1) f is orbitally continuous or
(e2) f is orbitally X≤-continuous and there exists a subsequence of {fn (x0)} such that
of {fn (x0)} such that for any k ∈ N ;
for any k ∈ N ;
-
(f)
there is a comparison function φ : R + → R + such that

for any (x, y) ∈ X≤, where

-
(g)
the metric d is complete,
Then, f is PO.
Corollary 2.7. Let (X, d, ≤) be an ordered metric space and f : X → X be an operator.
Let p be a w-distance on (X, d) and suppose that
-
(a)
if x, y ∈ X with (x, y)X ≤, then there exists c(x, y) ∈ X such that (x, c(x, y)) ∈ X ≤ and (y, c(x, y)) ∈ X ≤ ;
-
(b)
f is increasing or decreasing;
-
(c)
there exists x 0 ∈ X such that (x 0, f (x 0)) ∈ X ≤ ;
-
(d)
(d 1) f is orbitally continuous or
(d2) f is orbitally X≤-continuous and there exists a subsequence of {fn (x0)} such that
of {fn (x0)} such that for any k ∈ N ;
for any k ∈ N ;
-
(e)
there is a comparison function φ : R + → R + such that
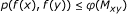
for any (x, y) ∈ X≤, where

-
(f)
the metric d is complete,
Then, f is PO.
References
Nieto JJ, Rodriguez-Lopez R: Contractive mapping theorems in partially ordered sets and applications to ordinary differential equations. Order 2005, 22: 223–239. 10.1007/s11083-005-9018-5
Nieto JJ, Rodriguez-Lopez R: Existence and uniqueness of fixed point in partially ordered sets and applications to ordinary differential equations. Acta Math Sin Eng 2007, 23: 2205–2212. 10.1007/s10114-005-0769-0
Ran AC, Breurings MC: A fixed point theorems in partially ordered sets and some applications to metric equations. Proc Am Math Soc 2004, 132: 1435–1443. 10.1090/S0002-9939-03-07220-4
Petrusel A, Rus IA: Fixed point theorems in ordered L -spaces. Proc Amer Math Soc 2006, 134: 411–418.
Kada O, Suzuki T, Takahashi W: Nonconvex minimization theorems and fixed point theorems in complete metric spaces. Math Jpn 1996, 44: 381–391.
Suzuki T: Fixed point theorems in complete metric spaces. In Nonlinear Analysis and Convex Analysis. Volume 939. Edited by: Takahashi W. RIMS, Kokyurku; 1996:173–182.
Suzuki T: Several fixed point theorem in complete metric spaces. Yokohama Math J 1997, 44: 61–72.
Suzuki T: Generalized distance and existence theorems in complete metric spaces. J Math Anal Appl 2001, 253: 440–458. 10.1006/jmaa.2000.7151
Suzuki T, Takahashi W: Fixed point theorems and characterizations of metric completeness. Topol Methods Nonlinear Anal 1996, 8: 371–382.
Saadati R, Vaezpour SM: Monotone generalized weak contractions in partially ordered metric spaces. Fixed Point Theory 2010,11(2):375–382.
Shioji N, Suzuki T, Takahashi W: Contractive mappings, Kannan mappings and metric completeness. Proc Am Math Soc 1998, 126: 3117–3124. 10.1090/S0002-9939-98-04605-X
O'Regan D, Petrusel A: Fixed point theorems for generalized contractions in ordered metric spaces. J Math Anal Appl 2008, 341: 1241–1252. 10.1016/j.jmaa.2007.11.026
Agarwal RP, El-Gebeilly MA, O'Regan D: Generalized contractions in partially ordered metric spaces. Appl Anal 2008, 87: 109–116. 10.1080/00036810701556151
Wu Y: New fixed point theorems and applications of mixed monotone operator. J Math Anal Appl 2008, 341: 883–893. 10.1016/j.jmaa.2007.10.063
Gnana Bhaskar T, Lakshmikantham V: Fixed point theorems in partially ordered metric spaces and applications. Nonlinear Anal 2006, 65: 1379–1393. 10.1016/j.na.2005.10.017
Acknowledgements
The authors would like to thank the referees and area editor Professor Simeon Reich for giving useful suggestions and comments for the improvement of this article. Y. J. Cho was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
All authors carried out the proof. All authors conceived of the study, and participated in its design and coordination. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Graily, E., Vaezpour, S.M., Saadati, R. et al. Generalization of fixed point theorems in ordered metric spaces concerning generalized distance. Fixed Point Theory Appl 2011, 30 (2011). https://doi.org/10.1186/1687-1812-2011-30
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-30