- Research
- Open access
- Published:
Another weak convergence theorems for accretive mappings in banach spaces
Fixed Point Theory and Applications volume 2011, Article number: 26 (2011)
Abstract
We present two weak convergence theorems for inverse strongly accretive mappings in Banach spaces, which are supplements to the recent result of Aoyama et al. [Fixed Point Theory Appl. (2006), Art. ID 35390, 13pp.].
2000 MSC: 47H10; 47J25.
1. Introduction
Let E be a real Banach space with the dual space E*. We write 〈x, x* 〉 for the value of a functional x*∈ E* at x ∈ E. The normalized duality mapping is the mapping J : E → 2E* given by

In this paper, we assume that E is smooth, that is,  exists for all x, y ∈ E with ||x|| = ||y|| = 1. This implies that J is single-valued and we do consider the singleton Jx as an element in E*. For a closed convex subset C of a (smooth) Banach space E, the variational inequality problem for a mapping A : C → E is the problem of finding an element u ∈ C such that
exists for all x, y ∈ E with ||x|| = ||y|| = 1. This implies that J is single-valued and we do consider the singleton Jx as an element in E*. For a closed convex subset C of a (smooth) Banach space E, the variational inequality problem for a mapping A : C → E is the problem of finding an element u ∈ C such that

The set of solutions of the problem above is denoted by S(C, A). It is noted that if C = E, then S(C, A) = A-10 := {x ∈ E : Ax = 0}. This problem was studied by Stampacchia (see, for example, [1, 2]). The applicability of the theory has been expanded to various problems from economics, finance, optimization and game theory.
Gol'shteĭn and Tret'yakov [3] proved the following result in the finite dimensional space ℝ N .
Theorem 1.1. Let α > 0, and let A : ℝN→ ℝNbe an α-inverse strongly monotone mapping, that is, 〈Ax - Ay, × - y〉 ≥ α||Ax - Ay||2for all x, y ∈ ℝN. Suppose that {x n } is a sequence in ℝNdefined iteratively by x1 ∈ ℝNand

where {λ n }⊂ [a, b] ⊂ (0, 2α). If A-1 0 ≠ ∅, then {x n } converges to some element of A-10.
The result above was generalized to the framework of Hilbert spaces by Iiduka et al. [4]. Note that every Hilbert space is uniformly convex and 2-uniformly smooth (the related definitions will be given in the next section). Aoyama et al. [[5], Theorem 3.1] proved the following result.
Theorem 1.2. Let E be a uniformly convex and 2-uniformly smooth Banach space with the uniform smoothness constant K, and let C be a nonempty closed convex subset of E. Let Q C be a sunny nonexpansive retraction from E onto C, let α > 0 and let A : C → E be an α-inverse strongly accretive mapping with S(C, A) ≠ ∅. Suppose that {x n } is iteratively defined by

where {α n } ⊂ [b, c] ⊂ (0, 1) and {λ n } ⊂ [a, α/K2] ⊂ (0, α/K2]. Then, {x n } converges weakly to some element of S(C, A).
Motivated by the result of Aoyama et al., we prove two more convergence theorems for α-inverse strongly accretive mappings in a Banach space, which are supplements to Theorem 1.2 above. The first one is proved without the presence of the uniform convexity, while the last one is proved in uniformly convex space with some different control conditions on the parameters.
The paper is organized as follows: In Section 2, we collect some related definitions and known fact, which are referred in this paper. The main results are presented in Section 3. We start with some common tools in proving the main results in Section 3.1. In Section 3.2, we prove the first weak convergence theorem without the presence of uniform convexity. The second theorem is proved in uniformly convex Banach spaces in Section 3.3.
2. Definitions and related known fact
Let E be a real Banach space. If {x
n
} is a sequence in E, we denote strong convergence of {x
n
} to x ∈ E by x
n
→ x and weak convergence by x
n
⇀ x. Denote by ω
w
({x
n
}) the set of weakly sequential limits of the sequence {x
n
}, that is, ω
w
({x
n
}) = {p : there exists a subsequence  of {x
n
} such that
of {x
n
} such that  }. It is known that if {x
n
} is a bounded sequence in a reflexive space, then ω
w
({x
n
}) = ∅.
}. It is known that if {x
n
} is a bounded sequence in a reflexive space, then ω
w
({x
n
}) = ∅.
The space E is said to be uniformly convex if for each ε ∈ (0, 2) there exists δ > 0 such that for any x, y ∈ U := {z ∈ E : ||z|| = 1}

The following result was proved by Xu.
Lemma 2.1 ([6]). Let E be a uniformly convex Banach space, and let r > 0. Then, there exists a strictly increasing, continuous and convex function g : [0, 2r] → [0, ∞) such that g(0) = 0 and

for all α ∈ [0, 1] and x, y ∈ B r := {z ∈ E : ||z|| ≤ r}.
The space E is said to be smooth if the limit

exists for all x, y ∈ U. The norm of E is said to be Fréchet differentiable if for each x ∈ U, the limit (2.1) is attained uniformly for y ∈ U.
Let C be a nonempty subset of a smooth Banach space E and α > 0. A mapping A : C → E is said to be α-inverse strongly accretive if

for all x, y ∈ C. It follows from (2.2) that A is  -Lipschitzian, that is,
-Lipschitzian, that is,

A Banach space E is 2-uniformly smooth if there is a constant c > 0 such that 〉 E (τ) ≤ cτ2 for all τ > 0 where

In this case, we say that a real number K > 0 is a 2-uniform smoothness constant of E if the following inequality holds for all x, y ∈ E:

Note that every 2-uniformly smooth Banach space has the Fréchet differentiable norm and hence it is reflexive.
The following observation extracted from Lemma 2.8 of [5] plays an important role in this paper.
Lemma 2.2. Let C be a nonempty closed convex subset of a 2-uniformly smooth Banach space E with a 2-uniform smoothness constant K. Suppose that A : C → E is an α-inverse strongly accretive mapping. Then, the following inequality holds for all x, y ∈ C and λ ∈ ℝ:

where I is the identity mapping. In particular, if , then I - λA is nonex pansive, that is, ||(I - λA)x - (I - λA)y|| ≤ ||x - y|| for all x, y ∈ C.
, then I - λA is nonex pansive, that is, ||(I - λA)x - (I - λA)y|| ≤ ||x - y|| for all x, y ∈ C.
Let C be a subset of a Banach space E. A mapping Q : E → C is said to be:
-
(i)
sunny if Q(Qx + t(x - Qx)) = Qx for all t ≥ 0;
-
(ii)
a retraction if Q 2 = Q.
It is known that a retraction Q from a smooth Banach space E onto a nonempty closed convex subset C of E is sunny and nonexpansive if and only if 〈x-Qx, J(Qx-y)〉 ≥ 0 for all x ∈ E and y ∈ C. In this case, Q is uniquely determined. Using this result, Aoyama et al. obtained the following result. Recall that, for a mapping T : C → E, the set of fixed points of T is denoted by F (T), that is, F (T) = {x ∈ C : x = Tx}.
Lemma 2.3 ([5]). Let C be a nonempty closed convex subset of a smooth Banach space
E. Let Q C be a sunny nonexpansive retraction from E onto C, and let A : C → E be a mapping. Then, for each λ > 0,

The space E is said to satisfy Opial's condition if

whenever x n ⇀ x ∈ E and y ∈ E satisfy x ≠ y. The following results are known from theory of nonexpansive mappings. It should be noted that Oplial's condition and the Fréchet differentiability of the norm are independent in uniformly convex space setting.
Lemma 2.4 ([7], [8]). Let C be a nonempty closed convex subset of a Banach space. E. Suppose that E is uniformly convex or satisfies Opial's condition. Suppose that T is a nonexpansive mapping of C into itself. Then, I - T is demiclosed at zero, that is, if {x n } is a sequence in C such that x n ⇀ p and x n - Tx n → 0, then p = Tp.
Lemma 2.5 ([9]). Let C be a nonempty closed convex subset of a uniformly convex Banach space with a Fréchet differentiable norm. Suppose that is a sequence of nonexpansive mappings of C into itself with
is a sequence of nonexpansive mappings of C into itself with . Let x ∈ C and S
n
= T
n
Tn-1· · · T1for all n ≥ 1. Then, the set
. Let x ∈ C and S
n
= T
n
Tn-1· · · T1for all n ≥ 1. Then, the set

consists of at most one element, where D is the closed convex hull of D.
D is the closed convex hull of D.
The following two lemmas are proved in the absence of uniform convexity, and they are needed in Section 3.2.
Lemma 2.6 ([10]). Let {x n } and {y n } be bounded sequences in a Banach space and {α n } be a real sequence in [0, 1] such that 0 < lim infn→∞α n ≤ lim supn→∞α n < 1. Suppose that xn+1= α n x n + (1 - α n )y n for all n ≥ 1. If lim supn→∞(||yn+1- y n || - ||xn+1- x n ||) ≤ 0, then x n - y n → 0.
Lemma 2.7 ([11]). Let {z n } and {w n } be sequences in a Banach space and {α n } be a real sequence in [0, 1]. Suppose that zn+1= α n z n + (1 - α n )w n for all n ≥ 1. If the following properties are satisfied:
-
(i)
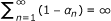 and lim infn→∞ α
n
> 0;
and lim infn→∞ α
n
> 0; -
(ii)
limn→∞||z n || = d and lim supn→∞||w n || ≤ d;
-
(iii)
the sequence
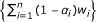 is bounded;
is bounded;
then d = 0.
We also need the following simple but interesting results.
Lemma 2.8 ([12]). Let {a n } and {b n } be two sequences of nonnegative real numbers.
If and an+1≤ a
n
+ b
n
for all n ≥ 1, then limn→∞a
n
exists.
and an+1≤ a
n
+ b
n
for all n ≥ 1, then limn→∞a
n
exists.
Lemma 2.9 ([13]). Let {a
n
} and {b
n
} be two sequences of nonnegative real numbers. If and
and , then lim infn→∞b
n
= 0.
, then lim infn→∞b
n
= 0.
3. Main results
From now on, we assume that
-
E is 2-uniformly smooth Banach space with a 2-uniform smoothness constant K;
-
C is a nonempty closed convex subset of E;
-
QC is a sunny nonexpansive retraction from E onto C;
-
A : C → E is an α-inverse strongly accretive mapping with S(C, A) ≠ ∅ and α > 0.
Suppose that {x n } is iteratively defined by

where {α
n
}⊂ [0, 1] and  . For convenience, we write y
n
≡ Q
C
(x
n
- λ
n
Ax
n
).
. For convenience, we write y
n
≡ Q
C
(x
n
- λ
n
Ax
n
).
3.1. Some properties of the sequence {x n } for weak convergence theorems
We start with some propositions, which are the common tools for proving the main results in the next two subsections.
Proposition 3.1. If p ∈ S(C, A), then limn→∞||x n - p|| exists, and hence, the sequences {x n } and {Ax n } are both bounded.
Proof. Let p ∈ S(C, A). By the nonexpansiveness of Q C (I - λ n A) for all n ≥ 1 and
Lemma 2.3, we have

for all n ≥ 1. This implies that

for all n ≥ 1. Therefore, limn→∞||x
n
- p|| exists, and hence, the sequence {x
n
} is bounded. Since A is  -Lipschitzian, we have {Ax
n
} is bounded. The proof is finished.
-Lipschitzian, we have {Ax
n
} is bounded. The proof is finished.
Proposition 3.2. The following inequality holds:

for all n ≥ 1.
Proof. Since Q C (I - λn+1A) and Q C are nonexpansive, we have

□
Proposition 3.3. Suppose that E is a reflexive Banach space such that either it is uniformly convex or it satisfies Opial's condition. Suppose that {x
n
} is a bounded sequence of C satisfying x
n
- Q
C
(I - λ
n
A)x
n
→ 0 and .
.
Then, {x n } converges weakly to some element of S(C, A).
Proof. Suppose that E is a uniformly convex Banach space or a reflexive Banach space satisfying Opial's condition. Then, ω
w
({x
n
}) ≠ ∅. We first prove that ω
w
({x
n
}) ⊂ S(C, A). To see this, let z ∈ ω
w
({x
n
}). Passing to a subsequence, if necessary, we assume that there exists a subsequence {n
k
} of {n} such that  and
and  . We observe that
. We observe that

This implies that  . By the nonexpansiveness of Q
C
(I - λA), Lemmas 2.3 and 2.4, we obtain that z ∈ F (Q
C
(I - λA)) = S(C, A). Hence ω
w
({x
n
}) ⊂ S(C, A).
. By the nonexpansiveness of Q
C
(I - λA), Lemmas 2.3 and 2.4, we obtain that z ∈ F (Q
C
(I - λA)) = S(C, A). Hence ω
w
({x
n
}) ⊂ S(C, A).
We next prove that ω w ({x n }) is exactly a singleton in the following cases.
Case 1: E is uniformly convex. We follow the idea of Aoyama et al. [5] in this case. For any n ≥ 1, we define a nonexpansive mapping T n : C → C by

We get that xn+1= T
n
Tn-1· · · T1x1 for all n ≥ 1. It follows from Lemma 2.3 that  . Applying Lemma 2.5, since every 2-uniformly smooth Banach space has Fréchet differentiable norm, gives
. Applying Lemma 2.5, since every 2-uniformly smooth Banach space has Fréchet differentiable norm, gives

consists of at most one element. But we know that

Therefore, ω w ({x n }) is a singleton.
Case 2: E satisfies Opial's condition. Suppose that p and q are two different elements of ω
w
({x
n
}). There are subsequences  and
and  of {x
n
} such that
of {x
n
} such that

Since p and q also belong to S(C, A), both limits limn→∞||x n -p|| and limn→∞||x n -q|| exist. Consequently, by Opial's condition,

This is a contradiction. Hence, ω w ({x n }) is a singleton, and the proof is finished. □
Remark 3.4. There exists a reflexive Banach space such that it satisfies Opial's condition but it is not uniformly convex. In fact, we consider E = ℝ2 with the norm ||(x, y)|| = |x| + |y| for all (x, y) ∈ ℝ2 . Note that E is finite dimensional, and hence it is reflexive and satisfies Opial's condition. To see that E is not uniformly convex, let x = (1, 0) and y = (0, 1), it follows that ||x - y|| = ||(1, -1)|| = 2 and ||x + y||/2 = ||(1/2, 1/2)|| = 1 ≰ 1 - δ for all δ > 0.
3.2. Convergence results without uniform convexity
In this subsection, we make use of Lemmas 2.6 and 2.7 to show that x n - y n → 0 under the additional restrictions on the sequences {α n } and {λ n }.
Proposition 3.5. Suppose that {α n }⊂ [c, d] ⊂ (0, 1) and λn+1- λ n → 0. Then, x n - y n → 0.
Proof. We will apply Lemma 2.6. Let us rewritten the iteration as

It follows from Proposition 3.1 that {x n } and {Ax n } are bounded. Then, {y n } = {(I - λ n A) x n } is bounded. Since λn+1- λ n → 0, it is a consequence of Proposition 3.2 that

Since all the requirements of Lemma 2.6 are satisfied, x n - y n → 0. □
Proposition 3.6. Suppose that {α n } and {λ n } satisfy the following properties:
-
(i)
{a n } ⊂ [c, 1) ⊂ (0, 1) and
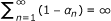 ;
; -
(ii)
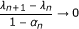 and
and 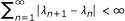 .
.
Then, x n - y n → 0.
Proof. We will apply Lemma 2.7. From the iteration, we have

where z
n
≡ x
n
- y
n
and  . Using Proposition 3.2, we obtain
. Using Proposition 3.2, we obtain

It follows from  and Lemma 2.8 that d := limn→∞||z
n
|| exists. We next prove that lim supn→∞||w
n
|| ≤ d. Again, by Proposition 3.2, we get
and Lemma 2.8 that d := limn→∞||z
n
|| exists. We next prove that lim supn→∞||w
n
|| ≤ d. Again, by Proposition 3.2, we get

Finally, for all n ≥ 1, we have

Hence, the sequence  is bounded. It follows then that d = 0. □
is bounded. It follows then that d = 0. □
We now have the following weak convergence theorems without uniform convexity.
Theorem 3.7. Let E be a 2-uniformly smooth Banach space satisfying Opial's condition. Let C be a nonempty closed convex subset of E. Let Q C be a sunny nonexpansive retraction from E onto C and A : C → E be an α-inverse strongly accretive mapping with S(C, A) ≠ ∅ and α > 0. Suppose that {x n } is iteratively defined by

where {α
n
} ⊂ [0, 1] and satisfy one of the following conditions:
satisfy one of the following conditions:
-
(i)
{α n } ⊂ [c, d] ⊂ (0, 1) and λ n+1- λ n → 0;
-
(ii)
{α n } ⊂ [c, 1) ⊂ (0, 1),
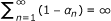 ,
, 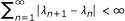 , and
, and 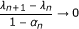 .
.
Then, {x n } converges weakly to an element in S(C, A).
Proof. Note that every 2-uniformly smooth Banach space is reflexive. The result follows from Propositions 3.3, 3.5 and 3.6. □
Remark 3.8. Conditions (i) and (ii) in Theorem 3.7 are not comparable.
-
(1)
If
 and {λ
n
} is a sequence in
and {λ
n
} is a sequence in  such that λ
n
- λ n+1→ 0 and 0 < lim infn→∞ λ
n
< lim supn→∞ λ
n
< 1, then {α
n
} and {λ
n
} satisfy condition (i) but fail condition (ii).
such that λ
n
- λ n+1→ 0 and 0 < lim infn→∞ λ
n
< lim supn→∞ λ
n
< 1, then {α
n
} and {λ
n
} satisfy condition (i) but fail condition (ii). -
(2)
If
 and
and 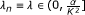 , then {α
n
} and {λ
n
} satisfy condition (ii) but fail condition (i).
, then {α
n
} and {λ
n
} satisfy condition (ii) but fail condition (i).
Remark 3.9. Note that the Opial property and uniform convexity are independent. Theorem 3.7 is a supplementary to Theorem 3.1 of Aoyama et al. [5].
3.3. Convergence results in uniformly convex spaces
In this subsection, we prove two more convergence theorems in uniformly convex spaces, which are also a supplementary to Theorem 3.1 of Aoyama et al. [5]. Let us start with some propositions.
Proposition 3.10. Assume that E is a uniformly convex Banach space. Suppose that {α n } and {λ n } satisfy the following properties:
-
(i)
{λ n } ⊂ [a, α/K 2] ⊂ (0, α/K 2];
-
(ii)
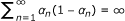 and
and  .
.
Then, x n - y n → 0.
Proof. Let p ∈ S(C, A). Note that limn→∞||x n - p|| exists and hence both {x n } and {y n } are bounded. By the uniform convexity of E and Lemma 2.1, there exists a continuous and strictly increasing function g such that

for all n ≥ 1. Hence, for each m ≥ 1, we have

In particular, . It follows from
. It follows from 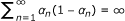 and Lemma 2.9 that lim infn→∞g(||x
n
- y
n
||) = 0. By the properties of the function g, we get that lim infn→∞||x
n
- y
n
|| = 0. Finally, we show that limn→∞||x
n
- y
n
|| actually exists. To see this, we consider the following estimate obtained directly from Proposition 3.2:
and Lemma 2.9 that lim infn→∞g(||x
n
- y
n
||) = 0. By the properties of the function g, we get that lim infn→∞||x
n
- y
n
|| = 0. Finally, we show that limn→∞||x
n
- y
n
|| actually exists. To see this, we consider the following estimate obtained directly from Proposition 3.2:

The assertion follows since  and Lemma 2.8. □
and Lemma 2.8. □
Let us recall the concept of strongly nonexpansive sequences introduced by Aoyama et al. (see [14]). A sequence of nonexpansive mappings {T n } of C is called a strongly nonexpansive sequence if x n - y n - (T n x n - T n y n ) → 0 whenever {x n } and {y n } are sequences in C such that {x n -y n } is bounded and ||x n -y n ||-||T n x n -T n y n || → 0. It is noted that if {T n } is a constant sequence, then this property reduces to the concept of strongly nonexpansive mappings studied by Bruck and Reich [15].
Proposition 3.11. Assume that E is a uniformly convex Banach space and {λ n }⊂ (0, b] ⊂ (0, α/K2). Then, {Q C (I - λ n A)} is a strongly nonexpansive sequence.
Proof. Notice first that Q C is a strongly nonexpansive mapping (see [16, 17]). Next, we prove that {I - λ n A} is a strongly nonexpansive sequence and then the assertion follows. Let {x n } and {y n } be sequences in C such that {x n - y n } is bounded and ||x n - y n ||-||(I - λ n A)x n - (I - λ n A)y n || → 0. It follows from Lemma 2.2 that

In particular, λ n Ax n - λ n Ay n → 0 and hence

Proposition 3.12. Assume that E is a uniformly convex Banach space. Suppose that α n ≡ 0 and {λ n } ⊂ (0, b] ⊂ (0, α/K2). Then, x n - y n → 0.
Proof. Let us rewritten the iteration as follows:

Let p ∈ S(C, A). Notice that p = Q C (I -λ n A)p for all n ≥ 1. Then, limn→∞||x n -p|| exists, and hence,

It follows from the preceding proposition that

□
We now obtain the following weak convergence theorems in uniformly convex spaces.
Theorem 3.13. Let E be a uniformly convex and 2-uniformly smooth Banach space. Let C be a nonempty closed convex subset of E. Let Q C be a sunny nonexpansive retraction from E onto C and A : C → E be an α-inverse strongly accretive mapping with S(C, A) ≠ ∅ and α > 0. Suppose that {x n } is iteratively defined by

where {α
n
} ⊂ [0, 1] and satisfy one of the following conditions:
satisfy one of the following conditions:
-
(i)
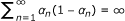 and
and
 ;
;
-
(ii)
α n ≡ 0 and {λ n }⊂ [a, b] ⊂ (0, α/K 2).
Then, {x n } converges weakly to an element in S (C, A).
Proof. The result follows from Propositions 3.3, 3.10 and 3.12. □
Remark 3.14. It is easy to see that conditions (i) and (ii) in Theorem 3.13 are not comparable.
Remark 3.15. Compare Theorem 3.13 to Theorem 1.2 of Aoyama et al., our result is a supplementary to their result. It is noted that, for example, our iteration scheme with α n ≡ 0 and λ n ≡ α/(α/K2) is simpler than the one in Theorem 1.2.
References
Kinderlehrer D, Stampacchia G: An introduction to variational inequalities and their applications. In Pure and Applied Mathematics. Volume 88. Academic Press, Inc., New York; 1980. xiv+313
Lions J-L, Stampacchia G: Variational inequalities. Comm Pure Appl Math 1967, 20: 493–519. 10.1002/cpa.3160200302
Gol'shteĭn EG, Tret'yakov NV: Modified Lagrangians in convex programming and their generalizations. Point-to-set maps and mathematical programming. Math Programming Stud 1979, 10: 86–97.
Iiduka H, Takahashi W, Toyoda M: Approximation of solutions of variational inequalities for monotone mappings. Panamer Math J 2004, 14: 49–61.
Aoyama K, Iiduka H, Takahashi W: Weak convergence of an iterative sequence for accretive operators in Banach spaces. Fixed Point Theory Appl Art 2006, 2006: 13. ID 35390
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Anal 1991, 16: 1127–1138. 10.1016/0362-546X(91)90200-K
Browder FE: Nonlinear operators and nonlinear equations of evolution in Banach spaces. Nonlinear functional analysis. In Proceedings of Symposia in Pure Mathematics, vol. XVIII, Part 2, Chicago, IL, 1968, pp. 1–308. American Mathematical Society, Providence; 1976.
Opial Z: Weak convergence of the sequence of successive approximations for nonexpansive mappings. Bull Am Math Soc 1967, 73: 591–597. 10.1090/S0002-9904-1967-11761-0
Reich S: Weak convergence theorems for nonexpansive mappings in Banach spaces. J Math Anal Appl 1979, 67: 274–276. 10.1016/0022-247X(79)90024-6
Suzuki T: Strong convergence theorems for infinite families of nonexpansive mappings in general Banach spaces. Fixed Point Theory Appl 2005, 2005: 103–123. 10.1155/FPTA.2005.103
Deng L: Convergence of the Ishikawa iteration process for nonexpansive mappings. J Math Anal Appl 1996, 199: 769–775. 10.1006/jmaa.1996.0174
Tan K-K, Xu HK: Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process. J Math Anal Appl 1993, 178: 301–308. 10.1006/jmaa.1993.1309
Ofoedu EU: Strong convergence theorem for uniformly L -Lipschitzian asymptotically pseudo-contractive mapping in real Banach space. J Math Anal Appl 2006, 321: 722–728. 10.1016/j.jmaa.2005.08.076
Aoyama K, Kimura Y, Takahashi W, Toyoda M: On a strongly nonexpansive sequence in Hilbert spaces. J Nonlinear Convex Anal 2007, 8: 471–489.
Bruck RE, Reich S: Nonexpansive projections and resolvents of accretive operators in Banach spaces. Houston J Math 1977, 3: 459–470.
Kitahara S, Takahashi W: Image recovery by convex combinations of sunny nonexpansive retractions. Topol Methods Nonlinear Anal 1993, 2: 333–342.
Reich S: A limit theorem for projections. Linear Multilinear Algebra 1983, 13: 281–290. 10.1080/03081088308817526
Acknowledgements
The first author is supported by the Thailand Research Fund, the Commission on Higher Education of Thailand and Khon Kaen University under Grant number 5380039. The second author is supported by grant fund under the program Strategic Scholarships for Frontier Research Network for the Ph.D. Program Thai Doctoral degree from the Office of the Higher Education Commission, Thailand. The third author is supported by the Thailand Research Fund through the Royal Golden Jubilee Ph.D. Program (Grant No. PHD/0188/2552) and Khon Kaen University under the RGJ--Ph.D. scholarship. Finally, the authors thank Professor M. de la Sen and the referees for their comments and suggestions.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
All authors contribute equally and significantly in this research work. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Saejung, S., Wongchan, K. & Yotkaew, P. Another weak convergence theorems for accretive mappings in banach spaces. Fixed Point Theory Appl 2011, 26 (2011). https://doi.org/10.1186/1687-1812-2011-26
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-26
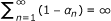 and lim infn→∞ α
n
> 0;
and lim infn→∞ α
n
> 0;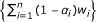 is bounded;
is bounded;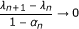 and
and 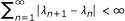 .
. and {λ
n
} is a sequence in
and {λ
n
} is a sequence in  such that λ
n
- λ n+1→ 0 and 0 < lim infn→∞ λ
n
< lim supn→∞ λ
n
< 1, then {α
n
} and {λ
n
} satisfy condition (i) but fail condition (ii).
such that λ
n
- λ n+1→ 0 and 0 < lim infn→∞ λ
n
< lim supn→∞ λ
n
< 1, then {α
n
} and {λ
n
} satisfy condition (i) but fail condition (ii). and
and 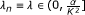 , then {α
n
} and {λ
n
} satisfy condition (ii) but fail condition (i).
, then {α
n
} and {λ
n
} satisfy condition (ii) but fail condition (i). .
.