- Research
- Open access
- Published:
Synchronal algorithm and cyclic algorithm for fixed point problems and variational inequality problems in hilbert spaces
Fixed Point Theory and Applications volume 2011, Article number: 21 (2011)
Abstract
We design synchronal algorithm and cyclic algorithm based on the general iterative algorithm proposed by Tian in 2010 for finding the common fixed point x* of finite family of strict pseudo-contractive mappings which is the solution of the variational inequality 〈(γ f - μF)x*, x - x*〉 ≤ 0,  .
.
2000 Mathematics Subject Classification: 58E35; 47H09; 65J15.
1. Introduction
Let H be a real Hilbert space with the inner product 〈·,·〉 and the norm || · ||, respectively. Let C be nonempty closed subset of H.
Recall that a mapping T : C → H is said to be k-strict pseudo-contraction if there exists a constant k ∈ [0, 1) such that

These mappings are extensions of nonexpansive mappings which satisfy the inequality (1.1) with k = 0. That is, T : C → H is nonexpansive if

We denote by F(T) the set of fixed points of the mapping T, that is

We assume that F(T) ≠ ∅ it is well known that F(T) is closed convex.
Let F : C → H be a nonlinear operator, we consider the problem of finding a point x* ∈ C such that

We denote by V I(F, C) the set of solutions of this variational inequality problem.
Takahashi [1] introduced a classical CQ algorithm as follows:

where T is nonexpansive mapping, and {αn} ⊂ [0, a] for some a ∈ [0, 1). Then they showed that {x n } converged strongly to PF(T)(x0) by the hybrid method in the mathematical programming. But it is hard to compute by this algorithm, because projection has to be used in every process.
The hybrid steepest descent method of Yamada [2] conquered this deficiency and proposed the following algorithm for solving the variational inequality.
Take x0 ∈ H arbitrarily and define {x n } by

where T is a nonexpansive mapping on H, F is L-Lipschitzian and η-strongly monotone with k > 0, η > 0, 0 < μ < 2η/L2. If {λ n } is a sequence in (0, 1) satisfying the following conditions:
-
(i)
limn→∞ λ n = 0;
-
(ii)
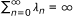
-
(iii)
either
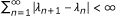 or
or  ,
,
then the sequence {x n } converged strongly to the unique solution of the variational inequality

Besides, he also proposed cyclic algorithm:

where T[n]= T n mod N, he also got strong convergence theorems.
On the other hand, Marino and Xu [3] considered the following general iterative method: an initial x0 is selected in H arbitrarily

where T is a nonexpansive mapping on H, f is a contraction, A is a linear bounded strongly positive operator, and {α n } is a sequence in (0, 1) satisfying the following conditions:
(C1) limn→∞α n = 0;
(C2) 
(C3) either  or
or  .
.
They proved that the sequence {x
n
} converged strongly to a fixed point  of T which solves the variational inequality
of T which solves the variational inequality

Very recently, Tian [4] combined the iterative method (1.3) with the Yamada's method (1.2) and considered the following general iterative method

where T is a nonexpansive mapping on H, f is a contraction, and F is k- Lipschitzian and η-strongly monotone with k > 0, η > 0, 0 < μ < 2η/k2.
He proved that if the sequence {α
n
} of parameters satisfies (C1)-(C3), then the sequence {x
n
} generated by (1.4) converged strongly to a fixed point  of T which solves the variational inequality
of T which solves the variational inequality

In this paper we designed two algorithms for finding a common fixed point x* of finite strict pseudo-contractions which also solves the variational inequality

where N ≥ 1 is a positive integer and  are N strict pseudo-contractions.
are N strict pseudo-contractions.
Let T be defined by

Where λ
i
> 0 such that  . We will show that the sequence {x
n
} generated by the algorithm:
. We will show that the sequence {x
n
} generated by the algorithm:

will converge strongly to a solution to the problem (1.6).
Another approach to the problem (1.6) is the cyclic algorithm. For each i = 1,..., N, let

where the constant β i satisfies k i < β i < 1. Beginning with x0 ∈ H, we define the sequence {x n } cyclically by

Indeed, the algorithm above can be written as

where T[n]= T i , with i = n(modN ), 1 ≤ i ≤ N. We will show that this cyclic algorithm (1.8) is also strongly convergent if the sequences {α n } and {β n } are appropriately chosen.
We will use the notations:
-
1.
⇀ for weak convergence and → for strong convergence.
-
2.
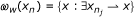 denotes the weak !-limit set of {x
n
}.
denotes the weak !-limit set of {x
n
}.
2. Preliminaries
We need some facts and tools which are listed as below.
Definition 1 A mapping F : C → H is called η-strongly monotone if there exists a positive constant η > 0 such that

Definition 2 B is called to be strongly positive bounded linear operator on
H, if there is a constant  with property
with property

Lemma 2.1. (see[5]) Let C be a nonempty closed convex subset of a real Hilbert space H and T : C ! C is a nonexpansive mapping. If a sequence {x n } in C such that x n ⇀ z and (I - T)x n → 0, then z = Tz.
Lemma 2.2. (see[6]) Let C be a nonempty closed convex subset of a real Hilbert space H. If T : C → C is a κ-strict pseudo-contraction, then the mapping I - T is demiclosed at 0. That is, if {x
n
} is a sequence in C such that and (I - T)x
n
→ 0, then
and (I - T)x
n
→ 0, then .
.
Lemma 2.3. (see[7]) Assume {a n } is a sequence of nonnegative real numbers such that

where {γ n } is a sequence in (0, 1) and {δ n } is a sequence in ℝ such that:
-
(i)
limn→∞ γ n = 0 and
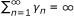 ;
; -
(ii)
limn→∞ δ n /γ n ≤ 0 or
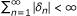 .
.
Then limn→∞a n = 0.
Lemma 2.4. (see[4]) Let H be a real Hilbert space, f : H → H a contraction with coefficient 0 < α < 1, and F : H → H a k-Lipschitzian continuous operator and η-strongly monotone operator with k > 0, η > 0. Then for 0 < γ < μη/α,

That is, μF - γf is strongly monotone with coefficient μη - γα.
Lemma 2.5. (see[8]) Suppose S : C → H is a k-strict pseudo-contraction. Define T : C → H by Tx = λx + (1 - λ)Sx for each × ∈ C. Then, as λ ∈ [k, 1), T is a nonexpansive mapping such that F(T) = F(S).
Lemma 2.6. (see[6]) Assume C is a closed convex subset of a Hilbert space H. Given an integer N ≥ 1, assume for each 1 ≤ i ≤ N, T
i
: C → C is a k
i
-strict pseudo-contraction for some 0 ≤ k
i
< 1. Assume is a positive sequence such that
is a positive sequence such that . Suppose that
. Suppose that then
then

Lemma 2.7. (see[9]) Assume T
i
: H → H is a k
i
-strict pseudo-contraction for some 0 ≤ k
i
< 1 (1 ≤ i ≤ N ): Let , k
i
< α
i
< 1 (1 ≤ i ≤ N), if
, k
i
< α
i
< 1 (1 ≤ i ≤ N), if , then
, then

Lemma 2.8. Let F : H → H be a η-strongly monotone and L-Lipschitzian operator with L > 0, η > 0. Assume that 0 < μ < 2η/L2,  and 0 < t < 1. Then ||(I - μtF)x - (I - μtF)y|| ≤ (1 - tτ) ||x - y||.
and 0 < t < 1. Then ||(I - μtF)x - (I - μtF)y|| ≤ (1 - tτ) ||x - y||.
Proof. Put g = I μtF, then

Therefore,

that is,

□
3. Synchronal algorithm
Theorem 3.1. Let H be a real Hilbert space and let T
i
: H → H be a k
i
-strict pseudo-contraction for some k
i
∈ (0, 1) (i = 1,..., N ) such that , f be a contraction with coefficient β ∈ (0, 1) and λ
i
be a positive constant such that
, f be a contraction with coefficient β ∈ (0, 1) and λ
i
be a positive constant such that . Let G : H → H be a η-strongly monotone and L-Lipschitzian operator with L > 0, η > 0. Assume that 0 < μ < 2η/L2,
. Let G : H → H be a η-strongly monotone and L-Lipschitzian operator with L > 0, η > 0. Assume that 0 < μ < 2η/L2,  . Given the initial guess x0 ∈ H chosen arbitrarily and given sequences {α
n
} and {β
n
} in (0, 1), satisfying the following conditions:
. Given the initial guess x0 ∈ H chosen arbitrarily and given sequences {α
n
} and {β
n
} in (0, 1), satisfying the following conditions:
(3.1a) limn→∞α
n
= 0,  ;
;
(3.1b)  ,
,  ;
;
(3.1c) 0 ≤ max i k i ≤ β n < a < 1 for all n ≥ 0;
let {x n } be the sequences define d by the composite process (1.7), i.e.

Then {x
n
} converges strongly to a common fixed point of which solves the variational inequality (1.6).
which solves the variational inequality (1.6).
Proof. Put  , then by Lemma 2.6, we conclude that T is a k-strict pseudo-contraction with k = max {k
i
: 1 ≤ i ≤ N} and
, then by Lemma 2.6, we conclude that T is a k-strict pseudo-contraction with k = max {k
i
: 1 ≤ i ≤ N} and  .
.
We can rewrite the algorithm (1.7) as

Furthermore, by Lemma 2.5, we conclude that  is a nonexpansive mapping and
is a nonexpansive mapping and  .
.
Step 1. {x n } is bounded.
Take  , from (1.7) and Lemma 2.9 we have
, from (1.7) and Lemma 2.9 we have

By simple induction, we have

Hence {x n } is bounded.
From  , we have v ∈ F (T ), hence
, we have v ∈ F (T ), hence

It follows that

So, we have

Therefore, {Tx n } is bounded.
G is L-Lipschitzian, so

{Tx
n
} is bounded, so  is bounded.
is bounded.
f is a contraction, so f(x n ) is bounded.
Step 2.

Observing that

we have

This in turn implies that

where M1 is an appropriate constant such that  . On the other hand, we note that
. On the other hand, we note that

where M2 is an appropriate constant such that M2 ≥ supn≥1{||x n - Tx n ||}. Substituting (3.3) into (3.2) yields

where M3 is an appropriate constant such that M3 ≥ max{M1, M2}. By conditions (3.1a) and (3.1b) and Lemma 2.3, we obtain that limn→∞||xn+1- x n || = 0.
From (1.7), we observe that

It follows from the condition (3.1a) and the boundedness of {f(x
n
)} and  that
that

On the other hand,

Hence, by condition (3.1c), we have

From (3.1) and (3.4), we obtain

From the boundedness of {x n }, we deduced that {x n } converges weakly. Assume x n ⇀ p, by Lemma 2.2 and (3.5), we obtain p = Tp. So, we have

Notice by Lemma 2.4, μG - γ f is strongly monotone, so the variational inequality (1.6) has a unique solution x* ∈ F(T).
Step 3.

Indeed, there exists a subsequence  such that
such that

Without loss of generality, we may further assume that  . It follows from (3.6) that x ∈ F(T). Since x* is the unique solution of (1.6), we obtain
. It follows from (3.6) that x ∈ F(T). Since x* is the unique solution of (1.6), we obtain

Step 4.

From Lemma 2.9, we have

This implies that

where  and
and  .
.  , from (3.1a), we have limn→∞γ
n
= 0; γ
n
≥ 2α
n
(τ - γβ), from (3.1a), we have
, from (3.1a), we have limn→∞γ
n
= 0; γ
n
≥ 2α
n
(τ - γβ), from (3.1a), we have 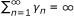 ; put M = sup {||x
n
- x*|| : n ∈ N}, we have
; put M = sup {||x
n
- x*|| : n ∈ N}, we have  . So, limn→∞δ
n
/γ
n
≤ 0. Hence, by Lemma 2.3, we conclude that x
n
→ x* as n → ∞. □
. So, limn→∞δ
n
/γ
n
≤ 0. Hence, by Lemma 2.3, we conclude that x
n
→ x* as n → ∞. □
4. Cyclic algorithm
Theorem 4.1. Let H be a real Hilbert space and let T
i
: H → H be a k
i
-strict pseudo-contraction for some k
i
∈ (0, 1) (i = 1,..., N ) such that and f be a contraction with coefficient β ∈ (0, 1). Let G : H → H be a η-strongly monotone and L-Lipschitzian operator with L > 0, η > 0. Assume that
and f be a contraction with coefficient β ∈ (0, 1). Let G : H → H be a η-strongly monotone and L-Lipschitzian operator with L > 0, η > 0. Assume that . Given the initial guess x0 ∈ H chosen arbitrarily and given sequences {α
n
} and {β
n
} in (0, 1), satisfying the following conditions:
. Given the initial guess x0 ∈ H chosen arbitrarily and given sequences {α
n
} and {β
n
} in (0, 1), satisfying the following conditions:
(4.1a) limn→∞α n = 0,
(4.1b)  ;
;
(4.1c)  , or
, or ;
;
(4.1d) β[n]∈ [k, 1), where k = max i {k i : 1 ≤ i ≤ N},
let {x n } be the sequences define d by the composite process (1.8), i.e.

where T[n]= T
i
, with i = n(modN ), 1 ≤ i ≤ N, namely, T[n]is one of T1, T2,..., T
N
circularly. Then {x
n
} converges strongly to a common fixed point of which solves the variational inequality (1.6).
which solves the variational inequality (1.6).
Proof. Step 1. {x
n
} is bounded. Take  , from (1.8) and Lemma 2.9 we have
, from (1.8) and Lemma 2.9 we have

By simple induction, we have

Hence {x n } is bounded.
From the proof of Step 1 in Section 3, we know that {T[n]x n }, {f (x n )}, {GA[n]x n } are bounded.

So, {A[n]x n } is bounded.
Step 2. limn→∞||xn+N- x n || = 0.
By (1.8) and Lemma 2.9, we have

where K1 is an appropriate constant such that K1 ≥ supn≥1{μ||GA[n+1]x n ||+ γ ||f(x n )||}. By conditions (4.1a), (4.1b), (4.1c) and Lemma 2.3, we obtain ||xn+N- x n || → 0 as n → ∞.
Step 3. limn→ ∞||x n - A[n+N]··· A[n+1]x n || = 0.
From (1.8), we observe that

It follows from the condition (4.1a) and the boundedness of {f(x n )} and {GA[n+1]x n } that

Recursively,

By condition (4.1d) and Lemma 2.5, we know that  is nonexpansive, so we get
is nonexpansive, so we get

Proceeded accordingly, we have

Note that

From all the expressions above, we obtain

Since

we conclude ||x n - A[n+N]··· A[n+1]x n || → 0(n → ∞).
Step 4.

Take a subsequence  , by step 3, we get
, by step 3, we get

Notice that, for each n
j
,  is some permutation of the mappings A1A2 ··· A
N
, since A1, A2,···, A
N
are finite, all the finite permutation are N!, there must be some permutation appears infinite times.
is some permutation of the mappings A1A2 ··· A
N
, since A1, A2,···, A
N
are finite, all the finite permutation are N!, there must be some permutation appears infinite times.
Without loss of generality, suppose this permutation is A1A2···A
N
, we can take a subsequence  such that
such that  and
and

By Lemma 2.5, we conclude that A1, A2,···, A
N
are all nonexpansive. It is easy to prove that  is nonexpansive, so A1A2···A
N
is.
is nonexpansive, so A1A2···A
N
is.
By Lemma 2.2, we have q = A1A2 ··· A N q. From Lemmas 2.5 and 2.7, we obtain

Step 5.

Indeed, there exists a subsequence  such that
such that

Without loss of generality, we may further assume that  . It follows from (4.2) that x ∈ F(T). Since x* is the unique solution of (1.6), we obtain
. It follows from (4.2) that x ∈ F(T). Since x* is the unique solution of (1.6), we obtain

Step 6. x n → x*(n → ∞).
From Lemma 2.9, we have

This implies that

where  and
and  .
.  , from (4.1a), we have limn→∞γ
n
= 0; γ
n
≥ 2α
n
(τ -γβ), from (4.1b), we have
, from (4.1a), we have limn→∞γ
n
= 0; γ
n
≥ 2α
n
(τ -γβ), from (4.1b), we have 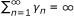 ; put M = sup {||x
n
- x*||: n ∈ N}, we have
; put M = sup {||x
n
- x*||: n ∈ N}, we have  . So, limsupn→∞δ
n
/γ
n
≤ 0. Hence, by Lemma 2.3, we conclude that x
n
→ x* as n → ∞. . □
. So, limsupn→∞δ
n
/γ
n
≤ 0. Hence, by Lemma 2.3, we conclude that x
n
→ x* as n → ∞. . □
Taking n = 1, β n = 0 and T is nonexpansive mapping in Theorems 3.1 and 4.1, we get
Corollary 1 (see[4]) Let {x n } be generated by the following algorithm

Assume the sequence {α n } satisfies conditions:
(C1) limn→∞α n = 0;
(C2)  ;
;
(C3) either  or
or 
then {x
n
} converged strongly to  which solves the variational inequality
which solves the variational inequality

Taking n = 1, β n = 0 and T is nonexpansive mapping, G = A, μ = 1 in Theorems 3.1 and 4.1, we get
Corollary 2 (see[3]) Let {x n } be generated by the following algorithm:

Assume the sequence {α
n
} satisfies conditions (C1)-(C3), then the sequence {x
n
} converged strongly to a fixed point  of T which solves the variational inequality
of T which solves the variational inequality

Taking n = 1, β n = 0 and T is nonexpansive mapping, γ = 0 in Theorem 3.1 and Theorem 4.1, we get:
Corollary 3 (see[2]) Let {x n } be generated by the following algorithm

where T is a nonexpansive mapping on H, F is L-Lipschitzian and η-strongly monotone with k > 0, η > 0, 0 < μ < 2η/L2. If {λ n } is a sequence in (0, 1) satisfies the following conditions:
-
(i)
limn→∞ λ n = 0;
-
(ii)
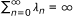 ;
; -
(iii)
either
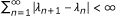 or
or 
then the sequence {x n } converged strongly to the unique solution of the variational inequality

Taking n = 1, β n = 0 and T is nonexpansive mapping, γ = 0 in Theorem 4.1, we get
Corollary 4 (see[2]) Let {x n } be generated by the following algorithm

where T[n]= T
n
mod N. Assume {λ
n
} satisfies conditions (C1)-(C3) and C = F(T
N
··· T 1) = F (T1T
N
··· T3T2) = ··· = F (TN - 1TN - 2··· T1T
N
), then {x
n
} converged strongly to the unique solution  of the variational inequality
of the variational inequality

References
Nakajo K, Takahashi W: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. J Math Anal Appl 2003, 279: 372–379. 10.1016/S0022-247X(02)00458-4
Yamada I: The hybrid steepest-descent method for variational inequality problems over the intersection of the fixed point sets of nonexpansive mappings. In Inherently Parallel Algorithms in Feasibility and Optimization and Their Applications. North-Holland, Amsterdam Edited by: Butnariu, D, Censor, Y, Reich S. 2001, 473–504.
Marino G, Xu HK: A general iterative method for nonexpansive mappings in Hilbert spaces. J Math Anal Appl 2006, 318: 43–52. 10.1016/j.jmaa.2005.05.028
Tian M: A general iterative algorithm for nonexpansive mappings in Hilbert spaces. Nonlinear Anal 2010, 73: 689–694. 10.1016/j.na.2010.03.058
Geobel K, Kirk WA: Topics in Metric Fixed Point Theory. In Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge; 1990.
Acedo GL, Xu HK: Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Anal 2007, 67: 2258–2271. 10.1016/j.na.2006.08.036
Xu HK: Iterative algorithms for nonlinear operators. J Lond Math Soc 2002, 66: 240–256. 10.1112/S0024610702003332
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. J Math Anal Appl 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
He SN, Liang XL: Hybrid steepest-descent methods for solving variational inequalities governed by boundedly Lipschitzian and strongly monotone operators. Fixed Point Theory Appl 2010.
Acknowledgements
The authors wish to thank the referees for their helpful comments, which notably improved the presentation of this manuscript. This work was supported by Fundamental Research Funds for the Central Universities (Grant no. ZXH2011C002).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no completing interests.
Authors' contributions
All the authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tian, M., Di, L. Synchronal algorithm and cyclic algorithm for fixed point problems and variational inequality problems in hilbert spaces. Fixed Point Theory Appl 2011, 21 (2011). https://doi.org/10.1186/1687-1812-2011-21
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-21
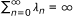
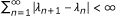 or
or  ,
,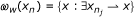 denotes the weak !-limit set of {x
n
}.
denotes the weak !-limit set of {x
n
}.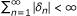 .
.