- Research
- Open access
- Published:
Convergence theorems of solutions of a generalized variational inequality
Fixed Point Theory and Applications volume 2011, Article number: 19 (2011)
Abstract
The convex feasibility problem (CFP) of finding a point in the nonempty intersection  is considered, where r ≥ 1 is an integer and each C
m
is assumed to be the solution set of a generalized variational inequality. Let C be a nonempty closed and convex subset of a real Hilbert space H. Let A
m
, B
m
: C → H be relaxed cocoercive mappings for each 1 ≤ m ≤ r. It is proved that the sequence {x
n
} generated in the following algorithm:
is considered, where r ≥ 1 is an integer and each C
m
is assumed to be the solution set of a generalized variational inequality. Let C be a nonempty closed and convex subset of a real Hilbert space H. Let A
m
, B
m
: C → H be relaxed cocoercive mappings for each 1 ≤ m ≤ r. It is proved that the sequence {x
n
} generated in the following algorithm:

where u ∈ C is a fixed point, {α
n
}, {β
n
}, {γ
n
}, {δ(1,n)}, ..., and {δ(r,n)} are sequences in (0, 1) and  ,
,  are positive sequences, converges strongly to a solution of CFP provided that the control sequences satisfies certain restrictions.
are positive sequences, converges strongly to a solution of CFP provided that the control sequences satisfies certain restrictions.
2000 AMS Subject Classification: 47H05; 47H09; 47H10.
1. Introduction and Preliminaries
Many problems in mathematics, in physical sciences and in real-world applications of various technological innovations can be modeled as a convex feasibility problem (CFP). This is the problem of finding a point in the intersection of finitely many closed convex sets in a real Hilbert spaces H. That is,

where r ≥ 1 is an integer and each C m is a nonempty closed and convex subset of H. There is a considerable investigation on CFP in the setting of Hilbert spaces which captures applications in various disciplines such as image restoration [1, 2], computer tomography [3] and radiation therapy treatment planning [4].
Throughout this paper, we always assume that H is a real Hilbert space, whose inner product and norm are denoted by 〈·, ·〉 and ||·||. Let C be a nonempty closed and convex subset of H and A: C → H a nonlinear mapping. Recall the following definitions:
-
(a)
A is said to be monotone if
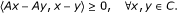
-
(b)
A is said to be ρ-strongly monotone if there exists a positive real number ρ > 0 such that
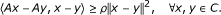
-
(c)
A is said to be η-cocoercive if there exists a positive real number η > 0 such that
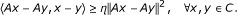
-
(d)
A is said to be relaxed η-cocoercive if there exists a positive real number η > 0 such that

-
(e)
A is said to be relaxed (η, ρ)-cocoercive if there exist positive real numbers η, ρ > 0 such that
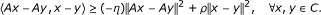
The main purpose of this paper is to consider the following generalized variational inequality. Given nonlinear mappings A : C → H and B : C → H, find a u ∈ C such that

where λ and τ are two positive constants. In this paper, we use GV I(C, B, A) to denote the set of solutions of the generalized variational inequality (1.2).
It is easy to see that an element u ∈ C is a solution to the variational inequality (1.2) if and only if u ∈ C is a fixed point of the mapping P C (τB - λA), where P C denotes the metric projection from H onto C. Indeed, we have the following relations:

Next, we consider a special case of (1.2). If B = I, the identity mapping and τ = 1, then the generalized variational inequality (1.1) is reduced to the following. Find u ∈ C such that

The variational inequality (1.4) emerging as a fascinating and interesting branch of mathematical and engineering sciences with a wide range of applications in industry, finance, economics, social, ecology, regional, pure and applied sciences was introduced by Stam-pacchia [5]. In this paper, we use V I(C, A) to denote the set of solutions of the variational inequality (1.4).
Let S : C → C be a mapping. We use F(S) to denote the set of fixed points of the mapping S. Recall that S is said to be nonexpansive if

It is well known that if C is nonempty bounded closed and convex subset of H, then the fixed point set of the nonexpansive mapping S is nonempty, see [6] more details. Recently, fixed point problems of nonexpansive mappings have been considered by many authors; see, for example, [7–16].
Recall that S is said to be demi-closed at the origin if for each sequence {x n } in C, x n ⇀ x0 and Sx n → 0 imply Sx0 = 0, where ⇀ and → stand for weak convergence and strong convergence.
Recently, many authors considered the variational inequality (1.4) based on iterative methods; see [17–32]. For finding solutions to a variational inequality for a cocoercive mapping, Iiduka et al. [22] proved the following theorem.
Theorem ITT. Let C be a nonempty closed convex subset of a real Hilbert space H and let A be an α-cocoercive operator of H into H with V I(C, A) ≠ ∅. Let {x n } be a sequence defined as follows. x1 = x ∈ C and

for every n = 1, 2, ..., where C is the metric projection from H onto C, {α n } is a sequence in [-1, 1], and {λ n } is a sequence in [0, 2α]. If {α n } and {λ n } are chosen so that {α n } ∈ [a, b] for some a, b with -1 < a < b < 1 and {λ n } ∈ [c, d] for some c, d with 0 < c < d < 2(1 + a)α, then {x n } converges weakly to some element of V I(C, A).
Subsequently, Iiduka and Takahashi [23] further studied the problem of finding solutions of the classical variational inequality (1.4) for cocoercive mappings (inverse-strongly monotone mappings) and nonexpansive mappings. They obtained a strong convergence theorem. More precisely, they proved the following theorem.
Theorem IT. Let C be a closed convex subset of a real Hilbert space H. Let S : C → C be a nonexpanisve mapping and A an α-cocoercive mapping of C into H such that F(S) ∩ V I(C, A) ≠ ∅. Suppose x1 = u ∈ C and {x n } is given by

for every n = 1, 2, ..., where {α n } is a sequence in [0, 1) and {λ n } is a sequence in [a, b].
If {α n } and {λ n } are chosen so that {λ n } ∈ [a, b] for some a, b with 0 < a < b < 2α,

then {x n } converges strongly to PF(S)∩V I(C,A)x.
In this paper, motivated by research work going on in this direction, we study the CFP in the case that each C m is a solution set of generalized variational inequality (1.2). Strong convergence theorems of solutions are established in the framework of real Hilbert spaces.
In order to prove our main results, we need the following lemmas.
Lemma 1.1 [33]. Let {x n } and {y n } be bounded sequences in a Hilbert space H and {β n } a sequence in (0, 1) with

Suppose that xn+1= (1 - β n )y n + β n x n for all integers n ≥ 0 and

Then limn→∞||y n - x n || = 0.
Lemma 1.2 [34]. Let C be a nonempty closed and convex subset of a real Hilbert space H. Let S1 : C → C and S2 : C → C be nonexpansive mappings on C. Suppose that F(S1) ∩ F (S2) is nonempty. Define a mapping S : C → C by

where a is a constant in (0, 1). Then S is nonexpansive with F(S) = F(S1) ∩ F (S2).
Lemma 1.3 [35]. Let C be a nonempty closed and convex subset of a real Hilbert space H and S : C → C a nonexpansive mapping. Then I - S is demi-closed at zero.
Lemma 1.4 [36]. Assume that {α n } is a sequence of nonnegative real numbers such that

where {γ n } is a sequence in (0, 1) and {δ n } is a sequence such that
-
(a)
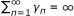 ;
; -
(b)
lim supn→∞δ n /γ n ≤ 0 or
 .
.
Then limn→∞α n = 0.
2. Main results
Theorem 2.1. Let C be a nonempty closed and convex subset of a real Hilbert space H. Let A
m
: C → H be a relaxed (η
m
, ρ
m
)-cocoercive and μ
m
-Lipschitz continuous mapping and B
m
: C → H a relaxed  -cocoercive and
-cocoercive and  -Lipschitz continuous mapping for each 1 ≤ m ≤ r. Assume that
-Lipschitz continuous mapping for each 1 ≤ m ≤ r. Assume that  . Let {x
n
} be a sequence generated in the following manner:
. Let {x
n
} be a sequence generated in the following manner:

where u ∈ C is a fixed point, {α n }, {β n }, {γ n }, {δ(1,n)}, ..., and {δ(r,n)} are sequences in (0, 1) satisfying the following restrictions:
-
(a)
 ;
; -
(b)
0 < lim infn→∞β n ≤ lim supn→∞β n < 1;
-
(c)
limn→∞α n = 0 and
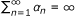 ;
; -
(d)
limn→∞δ(m,n)= δ m ∈ (0, 1), ∀1 ≤ m ≤ r,
And  ,
,  are two positive sequences such that
are two positive sequences such that
-
(e)
 .
.
Then the sequence {x
n
} generated in the iterative process (ϒ) converges strongly to a common element  , which uniquely solves the following variational inequality.
, which uniquely solves the following variational inequality.

Proof. First, we prove that the mapping P C (τ m B m - λ m A m ) is nonexpansive for each 1 ≤ m ≤ r. For each x, y ∈ C, we have

It follows from the assumption that each A m is relaxed (η m , ρ m )-cocoercive and μ m -Lipschitz continuous that

where  . This shows that
. This shows that

In a similar way, we can obtain that

where  . Substituting (2.2) and (2.3) into (2.1), we from the condition (e) see that P
C
(τ
m
B
m
- λ
m
A
m
) is nonexpansive for each 1 ≤ m ≤ r. Put
. Substituting (2.2) and (2.3) into (2.1), we from the condition (e) see that P
C
(τ
m
B
m
- λ
m
A
m
) is nonexpansive for each 1 ≤ m ≤ r. Put

Fixing  , we see that
, we see that

It follows that

By mathematical inductions we arrive at

Since the mapping P C (τ m B m - λ m A m ) is nonexpansive for each 1 ≤ m ≤ r, we see that

where M is an appropriate constant such that

Put  , for all n ≥ 1. That is,
, for all n ≥ 1. That is,

Now, we estimate ||ln+1- l n ||. Note that

which combines with (2.4) yields that

It follows from the conditions (b), (c) and (d) that

It follows from Lemma 1.1 that limn→∞||l n - x n || = 0. In view of (2.5), we see that x n +1 x n = (1 - β n )(l n - x n ). It follows that

On the other hand, from the iterative algorithm (ϒ), we see that x n +1 - x n = α n (u - x n ) + γ n (y n - x n ). It follows from (2.6) and the conditions (b), (c) that

Next, we show that  . To show it, we can choose a subsequence
. To show it, we can choose a subsequence  of {x
n
} such that
of {x
n
} such that

Since  is bounded, we obtain that there exists a subsequence
is bounded, we obtain that there exists a subsequence  of
of  which converges weakly to q. Without loss of generality, we may assume that
which converges weakly to q. Without loss of generality, we may assume that  . Next, we show that
. Next, we show that  . Define a mapping R : C → C by
. Define a mapping R : C → C by

where δ m = limn→∞δ(m,n). From Lemma 1.2, we see that R is nonexpansive with

Now, we show that Rx n - x n → 0 as n → ∞. Note that

From the condition (d) and (2.7), we obtain that limn→∞||Rx n - x n || = 0. From Lemma 1.3, we see that

In view of (2.8), we arrive at

Finally, we show that  as n - ∞. Note that
as n - ∞. Note that

which implies that

From the condition (c), (2.9) and applying Lemma 1.4 to (2.10), we obtain that

This completes the proof.
If B m ≡ I, the identity mapping and τ m ≡ 1, then Theorem 2.1 is reduced to the following result on the classical variational inequality (1.4).
Corollary 2.2. Let C be a nonempty closed and convex subset of a real Hilbert space H. Let A
m
: C → H be a relaxed (η
m
, ρ
m
)-cocoercive and μ
m
-Lipschitz continuous mapping for each 1 ≤ m ≤ r. Assume that  . Let {x
n
} be a sequence generated by the following manner:
. Let {x
n
} be a sequence generated by the following manner:

where u ∈ C is a fixed point, {α n }, {β n }, {γ n }, {δ(1,n)}, ..., and {δ(r,n)} are sequences in (0, 1) satisfying the following restrictions.
-
(a)
 ;
; -
(b)
0 < lim infn→∞β n ≤ lim supn→∞β n < 1;
-
(c)
limn→∞α n = 0 and
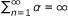 ;
; -
(d)
limn→∞δ(m,n)= δ m ∈ (0, 1), ∀1 ≤ m ≤ r, and
 is a positive sequence such that
is a positive sequence such that -
(e)
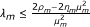 , ∀1 ≤ m ≤ r.
, ∀1 ≤ m ≤ r.
Then the sequence {x
n
} converges strongly to a common element  , which uniquely solves the following variational inequality
, which uniquely solves the following variational inequality

If r = 1, then Theorem 2.1 is reduced to the following.
Corollary 2.3. Let C be a nonempty closed and convex subset of a real Hilbert space H. Let A : C → H be a relaxed (η, ρ)-cocoercive and μ-Lipschitz continuous mapping and B : C → H a relaxed  -cocoercive and
-cocoercive and  -Lipschitz continuous mapping. Assume that GV I(C, B, A) is not empty. Let {x
n
} be a sequence generated in the following manner:
-Lipschitz continuous mapping. Assume that GV I(C, B, A) is not empty. Let {x
n
} be a sequence generated in the following manner:

where u ∈ C is a fixed point, {α n }, {β n } and {γ n } are sequences in (0, 1) satisfying the following restrictions.
-
(a)
α n + β n + γ n = 1, ∀ n ≥ 1;
-
(b)
0 < lim infn→∞β n ≤ lim supn→∞β n < 1;
-
(c)
limn→∞α n = 0 and
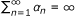
-
(d)
 .
.
Then the sequence {x
n
} converges strongly to a common element  , which uniquely solves the following variational inequality
, which uniquely solves the following variational inequality

For the variational inequality (1.4), we can obtain from Corollary 2.3 the following immediately.
Corollary 2.4. Let C be a nonempty closed and convex subset of a real Hilbert space H. Let A : C → H be a relaxed (η, ρ)-cocoercive and μ-Lipschitz continuous mapping. Assume that V I(C, A) is not empty. Let {x n } be a sequence generated in the following manner:

where u ∈ C is a fixed point, {α n }, {β n } and {γ n } are sequences in (0, 1) satisfying the following restrictions.
-
(a)
α n + β n + γ n = 1, ∀n ≥ 1;
-
(b)
0 < lim infn→∞β n ≤ lim supn→∞β n < 1;
-
(c)
limn→∞α n = 0 and
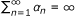 ;
; -
(d)
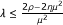 .
.
Then the sequence {x
n
} converges strongly to a common element  , which uniquely solves the following variational inequality
, which uniquely solves the following variational inequality

Remark 2.5. In this paper, the generalized variational inequality (1.2), which includes the classical variational inequality (1.4) as a special case, is considered based on iterative methods. Strong convergence theorems are established under mild restrictions imposed on the parameters. It is of interest to extend the main results presented in this paper to the framework of Banach spaces.
Abbreviations
- CFP:
-
convex feasibility problem.
References
Combettes PL: The convex feasibility problem: in image recovery. In Advances in Imaging and Electron Physics. Volume 95. Edited by: Hawkes P. Academic Press, Orlando; 1996:155–270.
Kotzer T, Cohen N, Shamir J: Images to ration by a novel method of parallel projection onto constraint sets. Opt Lett 1995, 20: 1172–1174. 10.1364/OL.20.001172
Sezan MI, Stark H: Application of convex projection theory to image recovery in tomograph and related areas. In Image Recovery: Theory and Application. Edited by: Stark H. Academic Press, Orlando; 1987:155–270.
Censor Y, Zenios SA: Parallel Optimization. Theory, Algorithms, and Applications, Numerical Mathematics and Scientific Computation. Oxford University Press, New York; 1997.
Stampacchia G: Formes bilineaires coercitives sur les ensembles convexes. CR Acad Sci Paris 1964, 258: 4413–4416.
Baillon JB: Quelques aspects de la theorie des points fixes dans les espaces de Banach. I, II, Séminaire d'Analyse Fonctionnelle (1978–1979). Exp. No. 7–8, Ecole Polytech., (in French). Palaiseau 1979, 45.
Qin X, Su Y: Approximation of a zero point of accretive operator in Banach spaces. J Math Anal Appl 2007, 329: 415–424. 10.1016/j.jmaa.2006.06.067
Qin X, Su Y: Strong convergence theorems for relatively nonexpansive mappings in a Banach space. Nonlinear Anal 2007, 67: 1958–1965. 10.1016/j.na.2006.08.021
Cho YJ, Kang SM, Qin X: Approximation of common fixed points of an infinite family of nonex-pansive mappings in Banach spaces. Comput Math Appl 2008, 56: 2058–2064. 10.1016/j.camwa.2008.03.035
Park S: Fixed point theorems in locally G-convex spaces. Nonlinear Anal 2002, 48: 869–879. 10.1016/S0362-546X(00)00220-0
Park S: Fixed point theory of multimaps in abstract convex uniform spaces. Nonlinear Anal 2009, 71: 2468–2480. 10.1016/j.na.2009.01.081
Qin X, Cho YJ, Kang JI, Kang SM: Strong convergence theorems for an infinite family of nonex-pansive mappings in Banach spaces. J Comput Appl Math 2009, 230: 121–127. 10.1016/j.cam.2008.10.058
Kim JK, Nam YM, Sim JY: Convergence theorems of implicit iterative sequences for a finite family of asymptotically quasi-nonexpansive type mappings. Nonlinear Anal 2009, 71: e2839-e2848. 10.1016/j.na.2009.06.090
Qin X, Cho YJ, Kang SM, Zho H: Convergence of a modified Halpern-type iteration algorithm for quasi- ϕ -nonexpansive mappings. Appl Math Lett 2009, 22: 1051–1055. 10.1016/j.aml.2009.01.015
Qin X, Cho SY, Zhou H: Common fixed points of a pair of non-expansive mappings with applications to convex feasibility problems. Glasgow Math J 2010, 52: 241–252. 10.1017/S0017089509990309
Wu C, Cho SY, Shang M: Moudafi's viscosity approximations with demi-continuous and strong pseudo-contractions for non-expansive semigroups. J Inequal Appl 2010, 2010: Article ID 645498.
Cho SY: Approximation of solutions of a generalized variational inequality problem based on iterative methods. Commun Korean Math Soc 2010, 25: 207–214. 10.4134/CKMS.2010.25.2.207
Kim JK, Cho SY, Qin X: Hybrid projection algorithms for generalized equilibrium problems and strictly pseudocontractive mappings. J Inequal Appl 2010, 2010: Article ID 312602.
Hao Y: Strong convergence of an iterative method for inverse strongly accretive operators. J Inequal Appl 2008, 2008: Article ID 420989.
Qin X, Cho YJ, Kang SM: Convergence theorems of common elements for equilibrium problems and fixed point problems in Banach spaces. J Comput Appl Math 2009, 225: 20–30. 10.1016/j.cam.2008.06.011
Qin X, Shang M, Su Y: Strong convergence of a general iterative algorithm for equilibrium problems and variational inequality problems. Math Comput Model 2008, 48: 1033–1046. 10.1016/j.mcm.2007.12.008
Iiduka H, Takahashi W, Toyoda M: Approximation of solutions of variational inequalities for monotone mappings. PanAmer Math J 2004, 14: 49–61.
Iiduka H, Takahashi W: Strong convergence theorems for nonexpansive mappings and inverse-strongly monotone mappings. Nonlinear Anal 2005, 61: 341–350. 10.1016/j.na.2003.07.023
Iiduka H, Takahashi W: Weak convergence of a projection algorithm for variational inequalities in a Banach space. J Math Anal Appl 2008, 339: 668–679. 10.1016/j.jmaa.2007.07.019
Qin X, Cho SY, Kang SM: Some results on generalized equilibrium problems involving a family of nonexpansive mappings. Appl Math Comput 2010, 217: 3113–3126. 10.1016/j.amc.2010.08.043
Park S, Kang BG: Generalized variational inequalities and fixed point theorems. Nonlinear Anal 1998, 31: 207–216. 10.1016/S0362-546X(96)00305-7
Park S, Kum S: An application of a Browder-type fixed point theorem to generalized variational inequalities. J Math Anal Appl 1998, 218: 519–526. 10.1006/jmaa.1997.5816
Park S: Fixed points, intersection theorems, variational inequalities, and equilibrium theorems. Int J Math Math Sci 2000,24(2):73–93. 10.1155/S0161171200002593
Park S, Chen MP: Generalized variational inequalities of the Hartman-Stampacchia-Browder type. J Inequal Appl 1998, 2: 71–87. 10.1155/S1025583498000046
Qin X, Chang SS, Cho YJ: Iterative methods for generalized equilibrium problems and fixed point problems with applications. Nonlinear Anal 2010, 11: 2963–2972. 10.1016/j.nonrwa.2009.10.017
Qin X, Cho YJ, Kang SM: Viscosity approximation methods for generalized equilibrium problems and fixed point problems with applications. Nonlinear Anal 2010, 72: 99–112. 10.1016/j.na.2009.06.042
Takahashi W, Toyoda M: Weak convergence theorems for nonexpansive mappings and monotone mappings. J Optim Theory Appl 2003, 118: 417–428. 10.1023/A:1025407607560
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter non-expansive semigroups without Bochne integrals. J Math Anal Appl 2005, 305: 227–239. 10.1016/j.jmaa.2004.11.017
Bruck RE: Properties of fixed point sets of nonexpansive mappings in Banach spaces. Trans Am Math Soc 1973, 179: 251–262.
Browder FE: Nonlinear operators and nonlinear equations of evolution in Banach spaces. Proc Symp Pure Math 1976, 18: 78–81.
Liu LS: Ishikawa and Mann iterative processes with errors for nonlinear strongly acretive mappings in Banach spaces. J Math Anal Appl 1995, 194: 114–125. 10.1006/jmaa.1995.1289
Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant no. 70871081 and Important Science and Technology Research Project of Henan province, China (102102210022).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
LY designed and performed all the steps of proof in this research and also wrote the paper. ML participated in the design of the study. All authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Yu, L., Liang, M. Convergence theorems of solutions of a generalized variational inequality. Fixed Point Theory Appl 2011, 19 (2011). https://doi.org/10.1186/1687-1812-2011-19
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-19
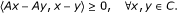
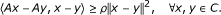
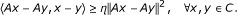

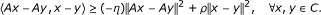
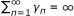 ;
; .
. ;
;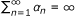 ;
; .
.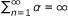 ;
;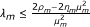 ,
,  .
.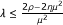 .
.