- Research
- Open access
- Published:
Convergence theorem for finite family of lipschitzian demi-contractive semigroups
Fixed Point Theory and Applications volume 2011, Article number: 18 (2011)
Abstract
Let E be a real Banach space and K be a nonempty, closed, and convex subset of E. Let  be a finite family of Lipschitzian demi-contractive semigroups of K, with sequences of bounded measurable functions L
i
: [0, ∞) → (0, ∞) and bounded functions λ
i
: [0, ∞) → (0, ∞), respectively, where
be a finite family of Lipschitzian demi-contractive semigroups of K, with sequences of bounded measurable functions L
i
: [0, ∞) → (0, ∞) and bounded functions λ
i
: [0, ∞) → (0, ∞), respectively, where  , i = 1,2, ..., N. Strong convergence theorem for common fixed point for finite family
, i = 1,2, ..., N. Strong convergence theorem for common fixed point for finite family  is proved in a real Banch space. As an application, a new convergence theorem for finite family of Lipschitzian demi-contractive maps is also proved.
is proved in a real Banch space. As an application, a new convergence theorem for finite family of Lipschitzian demi-contractive maps is also proved.
Mathematics subject classification (2000) 47H09, 47J25
1. Introduction
Let E be a real Banach space and E* be the dual space of E. The normalized duality mapping  is defined by, x ∈ E,
is defined by, x ∈ E,

where 〈., .〉 denotes the normalized duality pairing. For any x ∈ E, an element of
Jx is denoted by j(x).
Let K be a nonempty, closed and convex subset of E. Let T : K → K be a map, a point x ∈ K is called a fixed point of T if Tx = x, and the set of all fixed points of T is denoted by F(T). The mapping T is called L-Lipschitzian or simply Lipschitz if ∃L > 0, such that ||Tx -Ty|| ≤ L||x - y|| ∀x, y ∈ K and if L = 1, then the map T is called nonexpansive.
A one parameter family  of self mapping of K is called a nonexpansive semigroup if the following conditions are satisfied,
of self mapping of K is called a nonexpansive semigroup if the following conditions are satisfied,
-
(i)
T(0)x = x ∀ x ∈ K;
-
(ii)
T(t + s) = T(t) ∘ T(s) ∀ t, s ≥ 0;
-
(iii)
for each x ∈ K, the mapping t → T(t)x is continuos;
-
(iv)
for x, y ∈ K and t ≥ 0, ||T(t)x -T(t)y|| ≤ ||x - y||.
If the family  satisfies conditions (i) - (iii), then it is called
satisfies conditions (i) - (iii), then it is called
-
(a)
pseudocontractive semigroup if for any x, y ∈ K, there exists j(x - y) ∈ J(x - y) such that
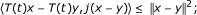
-
(b)
strictly pseudocontractive semigroup if there exists a bounded function λ : [0, ∞) → (0, ∞) and j(x - y) ∈ J(x - y) such that
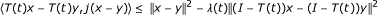
for all x, y ∈ K;
-
(c)
demi-contractive semigroup if F(T(t)) ≠ ∅ ∀t ≥ 0, there exists a bounded function λ : [0, ∞) → (0, ∞), and j(x - y) ∈ J(x - y) such that

for any x ∈ K and q ∈ F(T(t));
-
(d)
Lipschitzian semigroup if there is a bounded measurable function
L : [0, ∞) → (0, ∞) such that for x, y ∈ K and t ≥ 0,

It is known that every strictly pseudocontractive semigroup is Lipschitzian, and every strictly pseudocontractive semigroup with fixed point is demi-contractive semi-group.
Let E be a real Banach space and let K be a nonempty closed convex subset of E. A mapping T : K → K is demicompact if for every bounded sequence {x
n
} in K such that {xn - Tx
n
} converges, and there exists a subsequence, say  of {x
n
} that converges strongly to some x* in K. T is said to be demi-contractive if F(T) ≠ ∅, and there exists λ > 0 such that 〈Tx- q, j(x - q)〉 ≤ ||x - q||2 - λ||x - Tx||2 ∀ x ∈ K, q ∈ F(T) and j(x - q) ∈ J(x - q).
of {x
n
} that converges strongly to some x* in K. T is said to be demi-contractive if F(T) ≠ ∅, and there exists λ > 0 such that 〈Tx- q, j(x - q)〉 ≤ ||x - q||2 - λ||x - Tx||2 ∀ x ∈ K, q ∈ F(T) and j(x - q) ∈ J(x - q).
Let T1, T2, ..., T
N
be a family of self-mappings of K such that  . Then, the family is said to satisfy condition
. Then, the family is said to satisfy condition  if there exists a nondecreasing function f : [0, ∞) → [0, ∞) with f (0) = 0 and f (r) > 0 ∀ r ∈ (0, ∞) such that f (d(x, F)) ≤ ||x - T
s
x|| for some s in {1, 2, ..., N} and for all x ∈ K, where d(x, F) = inf {||x - q|| : q ∈ F}.
if there exists a nondecreasing function f : [0, ∞) → [0, ∞) with f (0) = 0 and f (r) > 0 ∀ r ∈ (0, ∞) such that f (d(x, F)) ≤ ||x - T
s
x|| for some s in {1, 2, ..., N} and for all x ∈ K, where d(x, F) = inf {||x - q|| : q ∈ F}.
Existence theorems for family of nonexpansive mappings are proved in [1–5] and actually many others. Recently, Suzuki [6] proved the equivalence between the fixed point property for nonexpansive mappings and that of the nonexpansive semi-groups.
Both implicit and explicit, Mann, Ishikawa, and Halpern-type schemes were studied for approximation of common fixed points of family of nonexpansive semigroups and their generalizations in various spaces; see, for example [6–13], to list but a few.
In 1998, Shoiji and Takahashi [7] introduced and studied a Halpern-type scheme for common fixed point of a family of asymptotically nonexpansive semigroup in the framework of a real Hilbert space. Suzuki [8] proved that the implicit scheme defined by x, x1 ∈ K,

converges strongly to a common fixed point of the family of nonexpansive semigroup in a real Hilbert space. Xu [9] extended the result of Suzuki to a more general real uniformly convex Banach space having a weakly sequentially continuous duality mapping.
In 2005, Aleyner and Reich [10] proved the strong convergence of an explicit Halpern-type scheme defined by x, x1 ∈ K,

to a common fixed point of the family {T(t) : t ≥ 0} of nonexpansive semigroup in a reflexive Banach space with uniformly Gatéuax differentiable norm. Recently, Zhang et al. [11] introduced and studied a composite iterative scheme defined by x, x1 ∈ K,

Those authors proved strong convergence of the sequence {x n } to a common fixed point of the family {T(t) : t ≥ 0} of nonexpansive semigroup.
Very recently, Chang et al. [12] proved a strong convergence theorem which extended and improved the results in [10, 9] and some others. They proved the following theorem.
Theorem 1.1. Chang et al. [12] Let K be a nonempty, closed, and convex subset of a real Banach space E: Let  be a Lipschitzian demi-contractive semigroup of K with bounded measurable function L : [0, ∞) → (0, ∞) and bounded function λ : [0, ∞) → (0, ∞) such that
be a Lipschitzian demi-contractive semigroup of K with bounded measurable function L : [0, ∞) → (0, ∞) and bounded function λ : [0, ∞) → (0, ∞) such that

Let {t n } be an increasing sequence in [0, ∞) and {α n } be a sequence in (0,1) satisfying the following conditions,
-
(i)
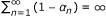 ; (ii)
; (ii)  . Assume that there exists a compact subset C of E such that ∪t≥0T(t)(K) ⊂ C and for any bounded set D ⊂ K
. Assume that there exists a compact subset C of E such that ∪t≥0T(t)(K) ⊂ C and for any bounded set D ⊂ K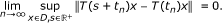
Let {x n } be generated by x1 ∈ K,

Then, the sequence {x n } converges strongly to some element in F.
The purpose in this article is to prove a strong convergence theorem for common fixed point for finite families  of demi-contractive semigroups in a real Banach space. As application, we also prove convergence theorem for finite family of demi-contractive mappings. Our theorems generalize and improve several recent results. For instance, Theorem 1.1, which generalized, extended and improved several recent results, is a special case of our Theorem.
of demi-contractive semigroups in a real Banach space. As application, we also prove convergence theorem for finite family of demi-contractive mappings. Our theorems generalize and improve several recent results. For instance, Theorem 1.1, which generalized, extended and improved several recent results, is a special case of our Theorem.
2. Preliminaries
We shall make use of the following lemmas.
Lemma 2.1. Let E be a real normed linear space. Then, the following inequality holds:

Lemma 2.2. (Xu [14]) Let {a n } and {b n } be sequences of nonnegative real numbers satisfying the inequality

If  , then
, then exists. If in addition {a
n
} has a subsequence which converges strongly to zero, then
exists. If in addition {a
n
} has a subsequence which converges strongly to zero, then  .
.
Lemma 2.3. (Suzuki [15]) Let {x n } and {y n } be bounded sequences in a Banach space E and let {β n } be a sequence in [0, 1] with 0 < lim inf β n ≤ lim supβ n < 1. Suppose xn+1= β n y n +(1 -β n )x n for all integers n ≥ 1 and lim sup(||yn+1- y n || - ||xn+1- x n ||) ≤ 0. Then, lim ||y n - x n || = 0.
3. Main Results
Let E be a real Banach space, and K be a nonempty, closed convex subset of E. For some fixed i ∈ ℕ, let  be a Lipschitzian demi-contractive semigroup with bounded measurable function L
i
: [0, ∞) → (0, ∞) and bounded function λ
i
: [0, ∞) → (0, ∞) such that
be a Lipschitzian demi-contractive semigroup with bounded measurable function L
i
: [0, ∞) → (0, ∞) and bounded function λ
i
: [0, ∞) → (0, ∞) such that

Then, for x, y ∈ K, q ∈ Fi and t ≥ 0,

and

Consider a family  of Lipschitzian demi-contractive semigroups of K and let
of Lipschitzian demi-contractive semigroups of K and let  ,
,  and
and  Clearly L < ∞ and λ > 0 and for x, y ∈ K,
Clearly L < ∞ and λ > 0 and for x, y ∈ K,  , t ≥ 0 and any i ∈ {1, 2, ..., N},
, t ≥ 0 and any i ∈ {1, 2, ..., N},

and

For a fixed δ ∈ (0, 1) and t ≥ 0 define a family S i (t) : K → K i = 1, 2, ..., N by

Then, for x, y ∈ K and  ,
,

Let  then
then

Also,

Let  .
.
Then,

Hence, for each i ∈ {1, 2, ... N}, S
i
is Lipschitz with Lipschitz constant  .
.
Lemma 3.1. Let E be a real Banach space and K be a nonempty closed convex subset of E. Let  be a finite family of Lipschitzian demi-contractive semigroups of K with sequences of bounded measurable functions L
i
: [0, ∞) → (0, ∞) and bounded functions λ
i
: [0, ∞) → (0, ∞) i = 1, 2, ..., N such that for each i = 1, 2, ..., N,
be a finite family of Lipschitzian demi-contractive semigroups of K with sequences of bounded measurable functions L
i
: [0, ∞) → (0, ∞) and bounded functions λ
i
: [0, ∞) → (0, ∞) i = 1, 2, ..., N such that for each i = 1, 2, ..., N,

Let  , {t
n
}be an increasing sequence in [0, ∞) and {α
n
} be a sequence in (0,1) satisfying the following conditions:
, {t
n
}be an increasing sequence in [0, ∞) and {α
n
} be a sequence in (0,1) satisfying the following conditions:
-
(i)
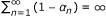 , (ii)
, (ii)  .
.
Assume ∀ i ∈ {1,2, ..., N} for any bounded set D ⊂ K the relation

holds. Let {x n } be a sequence generated by x1 ∈ K,

where T n (t n ) = T n modN (t n ).
Then,
-
(a)
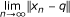 exists for all
exists for all  .
. -
(b)
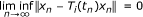 for all i ∈ {1,2,3, ..., N}.
for all i ∈ {1,2,3, ..., N}.
Proof. For any fixed  using (3.5), we have
using (3.5), we have

Thus,

where  .
.
Since  , by lemma 2.2, it follows that
, by lemma 2.2, it follows that  exists.
exists.
Hence, {x n } is bounded, which implies that {T n (t n )x n } and {S n (t n )x n } are also bounded.
From (3.6)

where,  . Hence, for some m ∈ ℕ,
. Hence, for some m ∈ ℕ,

Since m ∈ ℕ is arbitrary, we have

which implies

Next, we show that,

Let {β
n
} and {y
n
} be two sequences define by β
n
:= δ(1 - δ)αn+1+ δ2 and  . Then, using the definition of {β
n
} and {S
n
} we obtain that
. Then, using the definition of {β
n
} and {S
n
} we obtain that  . Then,
. Then,

Therefore,

Hence,

and by lemma 2.3,

Thus,

This implies that,

But, for i ∈ {1,2,3, ..., N},

Therefore,

Hence,

From the relation,

and condition (3.4) we get

It follows from (3.8) that  . This completes the proof. □
. This completes the proof. □
Theorem 3.2. Let E, K,  , {α
n
}, {t
n
},
, {α
n
}, {t
n
},  and {x
n
} be as in lemma 3.1. Assume that, for at least one i ∈ {1, 2, ..., N}, there exists a compact subset C of E such that ∪t≥0T
i
(t)(K) ⊂ C. Then, the sequence {x
n
} converges to some element
and {x
n
} be as in lemma 3.1. Assume that, for at least one i ∈ {1, 2, ..., N}, there exists a compact subset C of E such that ∪t≥0T
i
(t)(K) ⊂ C. Then, the sequence {x
n
} converges to some element  .
.
Proof. By Lemma 3.1, we have  .
.
If ∪t≥0T
s
(t)(K) ⊂ C for some compact subet C of E and some s ∈ {1, 2, ..., N}, then there exists a subsequence  , of {x
n
} and q* ∈ K, such that
, of {x
n
} and q* ∈ K, such that

Observe that for t > 0,

From the above we have  . Using (3.9) and the fact that Ts is Lipschitzian, we get q* ∈ ∩t≥0F(T
s
(t)).
. Using (3.9) and the fact that Ts is Lipschitzian, we get q* ∈ ∩t≥0F(T
s
(t)).
Now, for any l ∈ {1,2, ...,N }, since  , there exists a subsequence
, there exists a subsequence  of
of  such that
such that
 . Then, similarly for t ≥ 0, we obtain
. Then, similarly for t ≥ 0, we obtain

This implies that  and hence q* ∈ ∩t≥0F(T
l
(t)). Since l ∈ {1, 2, ... N} is arbitrarily chosen, we have
and hence q* ∈ ∩t≥0F(T
l
(t)). Since l ∈ {1, 2, ... N} is arbitrarily chosen, we have  . As the limit
. As the limit  exists, the conclusion of the theorem follows immediately and this completes the proof. □
exists, the conclusion of the theorem follows immediately and this completes the proof. □
Remark 3.3. Observe that considering a single one-parameter family of demi-contractive semigroup in Theorem 3.2, we obtain the conclusion of Theorem 1.1.
Let T1, T2, ..., T N be a finite family of Lipschitzian demi-contractive self-mapping of K with positive constants λ1, λ2, ..., λ N and Lipschitz constants L1,L2, ..., L N ,
respectively. Let  .
.
For a fixed δ ∈ (0, 1), define S n : K → K by

Then, it follows that for x, y ∈ K and i ∈ F,

where  ,
,  ,
,  and
and  .
.
The following Theorem is a consequence of Lemma 3.1.
Theorem 3.4. Let E, K and {α n } be as in Lemma 3.1. Let T1, T2, ..., T N : K → K be Lipschitzian demi-contractive mappings with T s demicompact for at least one s ∈ {1, 2, ..., N}. Let {x n ] be a sequence generated by x1 ∈ K

where T
n
= T
n
modN
. Then, {x
n
} converges strongly to a common fixed point of the family .
.
Proof. Following the line of proof of lemma 3.1 we immediately obtain  qk exists for any q ∈ F and
qk exists for any q ∈ F and  , ∀i ∈ {1,2, ... N}. Let
, ∀i ∈ {1,2, ... N}. Let  be a subsequence of {x
n
} such that
be a subsequence of {x
n
} such that

Therefore  and, by demicompactness of T
s
, there exists a subsequence
and, by demicompactness of T
s
, there exists a subsequence  of
of  and q* ∈ K, such that
and q* ∈ K, such that  as j → ∞.
as j → ∞.
Since,

we obtain q* ∈ F. But,  exists, thus x
n
→ q* ∈ F and this completes the proof. □
exists, thus x
n
→ q* ∈ F and this completes the proof. □
The following corollaries follow from Theorem 3.4
Corollary 3.5. Let E, K and {α
n
} be as in Theorem 3.4. Let T1, T2, ..., T
N
: K → K be Lipschitzian demi-contractive mappings. Suppose there exists a compact subset C in E such that  . Let {x
n
} be defined by (3.11). Then, {x
n
} converges strongly to a common fixed point of the family
. Let {x
n
} be defined by (3.11). Then, {x
n
} converges strongly to a common fixed point of the family  .
.
Corollary 3.6. Let E; K and {α
n
} be as in Theorem 3.4. Let T1, T2, ..., T
N
: K → K be Lipschitzian demi-contractive mappings satisfying condition  . Let {x
n
} be defined by (3.11). Then, {x
n
} converges strongly to a common fixed point of the family
. Let {x
n
} be defined by (3.11). Then, {x
n
} converges strongly to a common fixed point of the family  .
.
Proof. Following the line of proof of lemma 3.1, we obtain  for all i ∈ {1, 2, 3, ..., N} and ||xn+1- q||2 ≤ (1 + σn+1) ||x
n
- q||2, where
for all i ∈ {1, 2, 3, ..., N} and ||xn+1- q||2 ≤ (1 + σn+1) ||x
n
- q||2, where  . Since
. Since  , by lemma 2.2
, by lemma 2.2  exists and consequently
exists and consequently  exists. Let
exists. Let  be a subsequence of {x
n
} such that
be a subsequence of {x
n
} such that  . Then, by using condition
. Then, by using condition  , there exists s ∈ {1, 2, ..., N} such that
, there exists s ∈ {1, 2, ..., N} such that  and, using the property of f, we get that
and, using the property of f, we get that  , and since the limit
, and since the limit  exists we have that
exists we have that  . We next show that {x
n
} is Cauchy. Let ε > 0 be given, then there exists p* ∈ F and n* ∈ ℕ such that ∀n ≥ n*,
. We next show that {x
n
} is Cauchy. Let ε > 0 be given, then there exists p* ∈ F and n* ∈ ℕ such that ∀n ≥ n*,  . Hence, for n ≥ n* and k ∈ ℕ, we have
. Hence, for n ≥ n* and k ∈ ℕ, we have

Thus, {x
n
} is Cauchy and so x
n
→ q* ∈ K. We now show that q* is in F. Since  , there exists m0 ∈ ℕ large enough and p* ∈ F such that for all n ≥ m0,
, there exists m0 ∈ ℕ large enough and p* ∈ F such that for all n ≥ m0,  and
and  . Hence,
. Hence,

Thus, q* ∈ F(T l ) and since l ∈ {1, 2, ..., N} is arbitrary, we have q* ∈ F. This completes the proof. □
References
Belluce LP, Kirk WA: Fixed point theorem for families of contraction mappings. Pacific J Math 1966, 18: 213–217.
Browder FE: Nonexpansive nonlinear operators in Banach space. Proc Natl Acad Sci USA 1965, 54: 1041–1044. 10.1073/pnas.54.4.1041
Bruck RE: A common fixed point theorem for a commuting family of nonexpansive mappings. Pacific J Math 1974, 53: 59–71.
De Marr R: Common fixed points for commuting contraction mappings. Pacific J Math 1963, 13: 1139–1141.
Lim TC: A fixed point theorem for families of nonexpansive mappings. Pacific J Math 1974, 53: 487–493.
Suzuki T: Fixed point property for nonexpansive mappings versus that for nonexpansive semigroups. Nonlinear Anal 2009, 70: 3358–3361. 10.1016/j.na.2008.05.003
Shoiji N, Takahashi W: Strong convergence theorem for asymptotically nonexpansive semi-groups in Hilbert spaces. Nonlinear Anal 1998, 34: 87–99. 10.1016/S0362-546X(97)00682-2
Suzuki T: On strong convergence to a common fixed point of nonexpansive semigroups in Hilbert spaces. Proc Am Math Soc 2003, 131: 2133–2136. 10.1090/S0002-9939-02-06844-2
Xu HK: Strong convergence theorem for contraction semigroups in Banach spaces. Bull Austal Math Soc 2005, 72: 371–379. 10.1017/S000497270003519X
Aleyner A, Reich S: An explicit construction of sunny nonexpansive retraction in Banach spaces. Fixed Point Theory Appl 2005, 3: 295–305.
Zhang SS, Yang L, Liu JA: Strong convergence theorem for nonexpansive semigroups in Banach spaces. Appl Math Mech 2007, 28: 1287–1297. 10.1007/s10483-007-1002-x
Chang SS, Cho YJ, Lee HWJ, Chan C: Strong convergence theorems for Lipschitzian demicontraction semigroups in Banach spaces, Fixed Point Theory Application. 2011.
Zhang SS: Convergence theorem of common fixed points for Lipshitzian pseudocontraction semigroups in Banach spaces. Appl Math Mech 2009, 30: 145–152. 10.1007/s10483-009-0202-y
Xu HK: Inequalities in Banach spaces with applications. Nonlinear Anal 1991, 16: 1127–1138. 10.1016/0362-546X(91)90200-K
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. J Math Anal Appl 2005, 305: 227–239. 10.1016/j.jmaa.2004.11.017
Acknowledgements
This study was conducted when the first author was visiting the AbdusSalam International Center for Theoretical Physics Trieste Italy as an Associate, and the hospitality and financial support provided by the centre is gratefully acknowledged.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
BA conceived the study, GCU carried out the computations for Theorem 3.4. BA Modified Theorem 3.4 to obtain Theorem 3.2. Both authors read and approved the final manuscript.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Ali, B., Ugwunnadi, G.C. Convergence theorem for finite family of lipschitzian demi-contractive semigroups. Fixed Point Theory Appl 2011, 18 (2011). https://doi.org/10.1186/1687-1812-2011-18
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-18
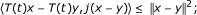
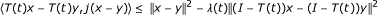

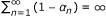 ; (ii)
; (ii)  . Assume that there exists a compact subset C of E such that
. Assume that there exists a compact subset C of E such that 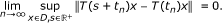
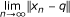 exists for all
exists for all 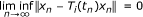 for all i
for all i