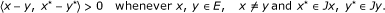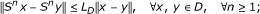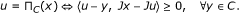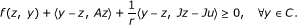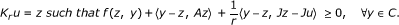A strong convergence theorem on solving common solutions for generalized equilibrium problems and fixed-point problems in Banach space

Abstract

In this paper, the common solution problem (P1) of generalized equilibrium problems for a system of inverse-strongly monotone mappings and a system of bifunctions satisfying certain conditions, and the common fixed-point problem (P2) for a family of uniformly quasi-ϕ-asymptotically nonexpansive and locally uniformly Lipschitz continuous or uniformly Hölder continuous mappings are proposed. A new iterative sequence is constructed by using the generalized projection and hybrid method, and a strong convergence theorem is proved on approximating a common solution of (P1) and (P2) in Banach space.

2000 MSC: 26B25, 40A05

1. Introduction

Recently, common solution problems (i.e., to find a common element of the set of solutions of equilibrium problems and/or the set of fixed points of mappings and/or the set of solutions of variational inequalities) with their applications have been discussed. Some authors such as in references [1–7] presented various iterative schemes and showed some strong or weak convergence theorems on common solution problems in Hilbert spaces. In 2008-2009, Takahashi and Zembayashi [8, 9] introduced several iterative sequences on finding a common solution of an equilibrium problem and a fixed-point problem for a relatively nonexpansive mapping, and established some strong or weak convergence theorems. In 2010, Chang et al. [10] discussed the common solution of a generalized equilibrium problem and a common fixed-point problem for two relatively nonexpansive mappings, and established a strong convergence theorem on the common solution problem. The frameworks of spaces in [8–10] are the uniformly smooth and uniformly convex Banach spaces. Chang et al. [11] established a strong convergence theorem on solving the common fixed-point problem for a family of uniformly quasi-ϕ-asymptotically nonexpansive and uniformly Lipschitz continuous mappings in a uniformly smooth and strictly convex Banach space with the Kadec-Klee property. Some other problems such as optimization problems (e.g. see [1, 4, 6]) and common zero-point problems (e.g. see [10]) are closely related to common solution problems.

Throughout this paper, unless other stated, ℝ and are denoted by the set of the real numbers and the set {1, 2,..., N}, respectively, where N is any given positive integer. Let E be a real Banach space with the norm || · ||, E* be the dual of E, and 〈·,·〉 be the pairing between E and E*. Suppose that C is a nonempty closed convex subset of E.

Let be N mappings and be N bifunctions. For each , the generalized equilibrium problem for f _k and A _k is to seek such that

(1.1)

The common solution problem (P1) of generalized equilibrium problems for and is to seek an element in , where and G(k) is the set of solutions of (1.1). We write G instead of in the case of N = 1.

Let be a family of mappings. The common fixed-point problem (P2) for is to seek an element in , where and F (S _i ) is the set of fixed points of S _i .

Motivated by the works in [8–11], in this paper we will produce a new iterative sequence approximating a common solution of (P1) and (P2) (i.e., some point belonging to ), and show a strong convergence theorem in a uniformly smooth and strictly convex Banach space with the Kadec-Klee property, where in (P2) is a family of uniformly quasi-ϕ-asymptotically nonexpansive mappings and for each i ≥ 1, S _i is locally uniformly Lipschitz continuous or uniformly Hölder continuous with order Θ _i .

2. Preliminaries

Let E be a real Banach space, and {x _n } be a sequence in E. We denote by x _n → x and x _n ⇀ x the strong convergence and weak convergence of {x _n }, respectively. The normalized duality mapping J : E → 2^E*is defined by

By the Hahn-Banach theorem, Jx ≠ ∅ for each x ∈ E.

A Banach space E is said to be strictly convex if for all x, y ∈ U = {u ∈ E : ||u|| = 1} with x ≠ y; to be uniformly convex if for each ε ∈ (0, 2], there exists γ > 0 such that for all x, y ∈ U with ||x - y|| ≥ ε; to be smooth if the limit

(2.1)

exists for every x, y ∈ U; to be uniformly smooth if the limit (2.1) exists uniformly for all x, y ∈ U.

Remark 2.1. The basic properties below hold (see [12]).

• (i) If E is a real uniformly smooth Banach space, then J is uniformly continuous on each bounded subset of E.

• (ii) If E is a strictly convex reflexive Banach space, then J^-1 is hemicontinuous, that is, J^-1 is norm-to-weak*-continuous.

• (iii) If E is a smooth and strictly convex reflexive Banach space, then J is single-valued, one-to-one and onto.

• (iv) Each uniformly convex Banach space E has the Kadec-Klee property, that is, for any sequence {x _n } ⊂ E, if x _n ⇀ x ∈ E and ||x _n || → ||x||, then x _n → x.

• (v) A Banach space E is uniformly smooth if and only if E* is uniformly convex.

• (vi) A Banach space E is strictly convex if and only if J is strictly monotone, that is,

  

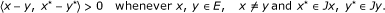
• (vii) Both uniformly smooth Banach spaces and uniformly convex Banach spaces are reflexive.

Now let E be a smooth and strictly convex reflexive Banach space. As Alber [13] and Kamimura and Takahashi [14] did, the Lyapunov functional ϕ : E × E → ℝ⁺ is defined by

It follows from [15] that ϕ(x, y) = 0 if and only if x = y, and that

(2.2)

Further suppose that C is a nonempty closed convex subset of E. The generalized projection (see [13]) Π _C : E→C is defined by for each x ∈ E,

A mapping A : C → E* is said to be δ-inverse-strongly monotone, if there exists a constant δ > 0 such that

A mapping S : C → C is said to be closed if for each {x _n } ⊂ C, x _n → x and Sx _n → y imply Sx = y; to be quasi-ϕ-asymptotically nonexpansive (see [16]) if F(S) ≠ ∅, and there exists a sequence {l _n } ⊂ [1, ∞) with l _n → 1 such that

It is easy to see that if A : C → E* is δ-inverse-strongly monotone, then A is -Lipschitz continuous. The class of quasi-ϕ-asymptotically nonexpansive mappings contains properly the class of relatively nonexpansive mappings (see [17]) as a subclass.

Definition 2.1 (see [11]). Let be a sequence of mappings. is said to be a family of uniformly quasi- ϕ -asymptotically nonexpansive mappings, if and there exists a sequence {l _n } ⊂ [1, ∞) with l _n → 1 such that for each i ≥ 1,

Now we introduce the following concepts.

Definition 2.2. A mapping S : C → C is said

• (1) to be locally uniformly Lipschitz continuous if for any bounded subset D in C, there exists a constant L _D > 0 such that

  

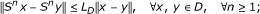
• (2) to be uniformly Hölder continuous with order Θ (Θ > 0) if there exists a constant L > 0 such that

  

Remark 2.2. It is easy to see that any uniformly Lipschitz continuous mapping (see [11]) is locally uniformly Lipschitz continuous, and is also uniformly Hölder continuous with order Θ = 1. However, the converse is not true.

Example 2.1. Suppose that S : ℝ → ℝ is defined by

Then S is locally uniformly Lipschitz continuous. In fact, for any bounded subset D in ℝ, setting M = 1 + sup{|x| : x ∈ D}, we have |Sⁿx - Sⁿy| ≤ 2M |x - y|, x, y ∈ D, ∀n ≥ 1. But S fails to be uniformly Lipschitz continuous.

Example 2.2. Suppose that S : ℝ - ℝ is defined by

S is uniformly Hölder continuous with order , since , ∀x, y ∈ ℝ, ∀n ≥ 1. But S fails to be uniformly Lipschitz continuous.

Lemma 2.1 (see [13, 14]). If C is a nonempty closed convex subset of a smooth and strictly convex reflexive Banach space E, then

• (1) ϕ(x, Π _C (y)) + ϕ(Π _C (y), y) ≥ ϕ(x, y), ∀x ∈ C, y ∈ E;

• (2) for × ∈ E and u ∈ C, one has

  

□

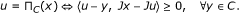
Lemma 2.2. Let E be a uniformly smooth and strictly convex Banach space with the Kadec-Klee property, {x _n } and{y _n } be two sequences of E, and . If and ϕ(x _n , y _n ) → 0, then .

Proof. We complete this proof by two steps.

Step 1. Show that there exists a subsequence of {y _n } such that .

In fact, since ϕ(x _n , y _n ) → 0, by (2.2) we have ||x _n || - ||y _n || → 0. It follows from that

(2.3)

and so

(2.4)

Then {Jy _n } is bounded in E*. It follows from Remark 2.1(v) and (vii) that E* is reflexive. Hence there exist a point f₀ ∈ E* and a subsequence of {Jy _n } such that

(2.5)

It follows from Remark 2.1(vii) and (iii) that there exists a point x ∈ E such that Jx = f₀. By the definition of ϕ, we obtain

By weak lower semicontinuity of norm || · ||, we have

which implies that and . It follows from Remark 2.1(iv) and (v) that E* has the Kadec-Klee property, and so by (2.4) and (2.5). By Remark 2.1(vii) and (ii), we have , which implies that by (2.3) and the Kadec-Klee property of E.

Step 2. Show that .

In fact, suppose that . For some given number ε₀ > 0, there exists a positive integer sequence {n _k } with n₁ < n₂ < · · · < n _k < · · ·, such that

(2.6)

Replacing {y _n } by in Step 1, there exists a subsequence of such that , which contradicts (2.6). □

Lemma 2.3. Let C be a nonempty closed convex subset of a smooth and strictly convex reflexive Banach space E, and let A : C → E* be a δ-inverse-strongly monotone mapping and f : C × C → ℝ be a bifunction satisfying the following conditions

(B₁) f(z, z) = 0, ∀z ∈ C;

(B₂) ;

(B₃) for any z ∈ C, the function y α f(z, y) is convex and lower semicontinuous;

(B₄) for some β ≥ 0 with β ≤ δ,

Then the following conclusions hold:

• (1) For any r > 0 and u ∈ E, there exists a unique point z ∈ C such that

  

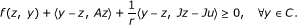  (2.7)

• (2) For any given r > 0, define a mapping K _r : E → C as follows: ∀u ∈ E,

  

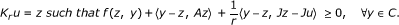
We have (i) F(K _r ) = G and G is closed convex in C, where

(ii) ϕ(z, K _r u) + ϕ(K _r u, u) ≤ ϕ(z, u), ∀z ∈ F(K _r ).

(3) For each n ≥ 1, r _n > a > 0 and u _n ∈ C with , we have

Proof. (1) We consider the bifunction instead of f. It follows from the proof of Lemma 2.5 in [10] that satisfies (B₁)-(B₃). Since A is δ-inverse-strongly monotone, by (B₄), we have

(2.8)

which implies is monotone. By Blum amd Oettli [18], for any r > 0 and u ∈ E, there exists z ∈ C such that (2.7) holds. Next we show that (2.7) has a unique solution. If for any given r > 0 and u ∈ E, z₁ and z₂ are two solutions of (2.7), then

and

Adding these two inequalities, we have

It follows from (2.8) that

which implies that z₁ = z₂ by Remark 2.1(vi).

(2) Since satisfies (B₁)-(B₃) and is monotone, the conclusion (2) follows from Lemmas 2.8 and 2.9 in [9].

(3) Since

we have

(2.9)

by the monotonicity of . It follows from . r _n > a > 0 and Remark 2.1(i) that

Since is convex and lower semicontinuous, it is also weakly lower semicontinuous. Letting n → ∞ in (2.9), we have , ∀y ∈ C. For any t ∈ (0, 1] and y ∈ C, setting , we have y _t ∈ C and , which together with (B₁) implies that

Thus f(y _t , y) + 〈y - y _t , Ay _t 〉 ≥ 0, ∀y ∈ C, ∀t ∈ (0, 1]. Letting t ↓ 0, since z α f(z, y) + 〈y - z, Az〉 satisfies (B₂), we have , ∀y ∈ C.

Remark 2.3. If β = 0 in (B₄), that is, f is monotone, then the conclusions (1) and (2) in Lemma 2.3 reduce to the relating results of Lemmas 2.5 and 2.6 in [10], respectively.

Next we give an example to show that there exist the mapping A and the bifunction f satisfying the conditions of Lemma 2.3. However, f is not monotone.

Example 2.3. Define A : ℝ → ℝ and f : ℝ × ℝ → ℝ by ∈ ∀x ∈ ℝ and , ∀(x, y) ∈ ℝ × ℝ, respectively. It is easy to see that A is -inverse-strongly monotone, f satisfies (B₁)-(B₃), and , ∀(x, y) : ℝ × ℝ with .

Lemma 2.4 (see [12]). Let C be a nonempty closed convex subset of a real uniformly smooth and strictly convex Banach space E with the Kadec-Klee property, S : C → C be a closed and quasi- ϕ -asymptotically nonexpansive mapping with a sequence {l _n } ⊂ [1, ∞), l _n → 1. Then F(S) is closed convex in C.

Lemma 2.5 (see [11]). Let E be a uniformly convex Banach space, η > 0 be a positive number and B _η (0) be a closed ball of E. Then, for any given sequence and for any given with , there exists a continuous, strictly increasing and convex function g : [0, 2η) → [0, ∞) with g(0) = 0 such that for any positive integers i, j with i < j,

□

3. Strong convergence theorem

In this section, let C be a nonempty closed convex subset of a real uniformly smooth and strictly convex Banach space E with the Kadec-Klee property.

Theorem 3.1. Suppose that

(C₁) for each , the mapping A _k : C → E* is δ _k -inverse-strongly monotone, the bifunction f _k : C × C → ℝ satisfies (B₁)-(B₃), and for some β _k ≥ 0 with β _k ≤ δ _k ,

(C₂) is a family of closed and uniformly quasi- ϕ -asymptotically nonexpansive mappings with a sequence {l _n } ⊂ [1, ∞), l _n → 1;

(C₃) for each i ≥ 1, S _i is either locally uniformly Lipschitz continuous or uniformly Hölder continuous with order Θ _i (Θ _i > 0), and is bounded in C.

(C₄) . Take the sequence generated by

where for each , with some a > 0, , and . If , ∀n ≥ 0 and lim inf_n→∞α_n,0α _{n, i} > 0, ∀i ≥ 1, then .

Proof. We shall complete this proof by seven steps below.

Step 1. Show that , , H _n and W _n for all n ≥ 0 are closed convex.

In fact, is closed convex since for each i ≥ 1, F(S _i ) is closed convex by (C₂) and Lemma 2.4. is closed convex since for each , G(k) is closed convex by (C₁) and Lemma 2.3(2)(i). H₀ = C is closed convex. Since ϕ(v,u_N,n) ≤ ϕ(v,x _n ) + ξ _n is equivalent to

we know that H _n (n ≥ 0) are closed convex. Finally, W _n is closed convex by its definition. Thus and are well defined.

Step 2. Show that {x _n } and are bounded.

From , ∀n ≥ 0 and Lemma 2.1(1), we have

(3.1)

which implies that {ϕ(x _n , x₀)} is bounded, and so is {x _n } by (2.2). It follows from (C₂) that for all , i ≥ 1, n ≥ 1,

Hence for all i ≥ 1, is uniformly bounded, and so is by (2.2). Obviously,

(3.2)

Step 3. Show that , ∀n ≥ 0.

Since Banach space E is uniformly smooth, E* is uniformly convex, by Remark 2.1(v). For any given , any n ≥ 1 and any positive integer j, by (C₂) and Lemma 2.5, we have

(3.3)

Put , , ∀n ≥ 0. It follows from (3.3) and Lemma 2.3(2)(ii) that

(3.4)

which implies that if , then p ∈ H _n , ∀n ≥ 0. Hence, , ∀n ≥ 0. By induction, now we prove that , ∀n ≥ 0. In fact, it follows from W₀ = C that . Suppose that for some m ≥ 0. By the definition of and Lemma 2.1(2), we have

and so

which shows z ∈ W_m+1, so .

Step 4. Show that there exists such that .

Without loss of generalization, we can assume that , since {x _n } is bounded and E is reflexive. Moreover, it follows that , ∀n ≥ 0 from H_n+1∩ W_n+1⊂ H _n ∩ W _n and the closeness and convexity of H _n ∩ W _n . Noting that

we have

by (3.1). It follows that

(3.5)

and so by . Hence,

(3.6)

by the Kadec-Klee property of E, and so

(3.7)

by Remark 2.1(i).

Step 5. Show that .

Since x_n+1∈ C, setting u = x_n+1in (3.1), we have

By (3.5),

(3.8)

By x_n+1∈ H_n+1, (3.2) and (3.8), we have

which together with (3.6) and Lemma 2.2 implies that

(3.9)

For any j ≥ 1 and any given , it follows from (3.2)-(3.4) and (3.9) that

(3.10)

which implies that

since , ∀i ≥ 1. We obtain

(3.11)

since g(0) = 0 and g is strictly increasing and continuous. By (3.7) and (3.11), we have and for all j ≥ 1. It follows from Remark 2.1(ii) that , which implies

(3.12)

by the uniform boundedness of and the Kadec-Klee property of E. Thus

By (C₃) and (3.6), we have

Hence, for each j ≥ 1,

By (3.12) and the closeness of S _j , we have for all j ≥ 1 and so .

Step 6. Show that .

In fact, it is easy to see that for each , and , the sequence {ϕ(p, u_k,n)} is bounded by (3.2), (3.4) and the boundedness of {x _n } and , which implies that {u_k,n} is bounded in C by (2.2). Since , by (3.2), (3.3), (3.5) and (3.10), we have

It follows from Lemma 2.2 that

(3.13)

Furthermore, it follows from (3.4) and Lemma 2.3(2)(ii) that for any given ,

which implies

by Remark 2.1(i), (3.9) and (3.13). Then by (3.13) and Lemma 2.2. Similarly, we also obtain . Hence, together with (3.9) and (3.13), for each ,

(3.14)

For each , since , we have

which together with (3.14) and Lemma 2.3(3) implies that , ∀y ∈ C. Therefore and so .

Step 7. Show that .

In fact, letting , by and , we have

It follows from (3.6) that

Hence, , and so . □

Setting N = 1, u₀, _n = y _n and u_N,n= u _n in Theorem 3.1, we can obtain the following result.

Corollary 3.1 Suppose that

(D₁) the mapping A : C → E* is a mapping with δ -inverse-strongly monotone, the bifunction f : C × C → ℝ satisfies (B₁)-(B₃) and for some β > 0 with β ≤ δ,

(D₂) both (C₂) and (C₃) hold, and Take the sequence generated by

where , for some a > 0 and. If , ∀ _n ≥ 0 and lim inf_n→∞α_n,0α_n,i> 0, ∀i ≥ 1, then . □

Furthermore, if S _i = S, i ≥ 1 in Corollary 3.1, the following corollary can be obtained immediately.

Corollary 3.2. Suppose that, besides (D1),

(E₁) S : C → C is closed and quasi- ϕ -asymptotically nonexpansive with {l _n } ⊂ [1, ∞), l _n → 1;

(E₂) S is either locally uniformly Lipschitz continuous or uniformly Hölder continuous with order Θ (Θ > 0), F(S) is bounded in C and F(S) ∩ G ≠ ∅. Take the sequence generated by

where , for some a > 0 and ξ = sup_u∈F(S)(l _n -1)ϕ(u, x _n ) . If lim inf_n→∞α _n (1- α _n ) > 0, then . □