A fixed point of generalized T _F -contraction mappings in cone metric spaces

Abstract

In this paper, the existence of a fixed point for T _F -contractive mappings on complete metric spaces and cone metric spaces is proved, where T : X → X is a one to one and closed graph function and F : P → P is non-decreasing and right continuous, with F^-1(0) = {-0} and F(t _n ) → 0 implies t _n → 0. Our results, extend previous results given by Meir and Keeler (J. Math. Anal. Appl. 28, 326-329, 1969), Branciari (Int. J. Math. sci. 29, 531-536, 2002), Suzuki (J. Math. Math. Sci. 2007), Rezapour et al. (J. Math. Anal. Appl. 345, 719-724, 2010), Moradi et al. (Iran. J. Math. Sci. Inf. 5, 25-32, 2010) and Khojasteh et al. (Fixed Point Theory Appl. 2010).

MSC(2000): 47H10; 54H25; 28B05.

1 Introduction

In 2007, Huang et al. [1], introduced the cone metric spaces and proved some fixed point theorems. Recently, Many results closely related to cone metric spaces are given (see [2–6]). In addition, some topological properties of these spaces are surveyed.

In 2010, Khojasteh et al. [7] introduced a new concept of integral with respect to a cone and proved some fixed point theorems in cone metric spaces. At the same year, Moradi et al. [8] introduced a new type of fixed point theorem by defining T _F -contraction as a new contractive condition in complete metric spaces. To state this result, some preliminaries from [8, 9] are recalled. First, set and

(1.1)

Definition 1.1. Let (X, d) be a metric space, f, T : X → X be two mappings and F ∈ Ψ. The mapping f is said to be T _F -contraction, if there exists α ∈ [0, 1) such that for all x, y ∈ X,

(1.2)

Example 1.2. Supposeis endowed with the Euclidean metric. Consider two mappings T, f : X → X defined byand fx = 2x, respectively. Obviously, f is not a contraction but it is a T _F -contraction, where F(x) ≡ x.

Definition 1.3. Let (X, d) be a metric space. A mapping T : X → X is said to be closed graph, if for every sequence {x _n } such that, there exists b ∈ X such that Tb = a. For example, the identity function on X is closed graph.

In 2010, Moradi et al. [8] proved the following fixed point theorem.

Theorem 1.4. Let (X, d) be a complete metric space, α ∈ [0, 1) and T, f : X → X be two mappings such that T is one-to-one and closed graph, and f is T _F - contraction, respectively, where F ∈ Ψ. Then, f has a unique fixed point a ∈ X. Also, for every x ∈ X, the sequence of iterates {Tfⁿx} converges to Ta.

2 Cone metric space

Let E be a real Banach space. A subset P of E is called a cone, if and only if, the following hold:

• P is closed, nonempty, and P ≠ {0},

• a, b ∈ ℝ, a, b ≥ 0, and x, y ∈ P imply that ax + by ∈ P,

• x ∈ P and -x ∈ P imply that x = 0.

Given a cone P ⊂ E, we define a partial ordering ≤ with respect to P by x ≤ y, if and only if, y -x ∈ P. We write x < y to indicate that x ≤ y but x ≠ y, while x ≪ y stand for y - x ∈ intP, where intP denotes the interior of P. The cone P is called normal, if there exist a number K > 0 such that, 0 ≤ x ≤ y implies ||x|| ≤ K ||y||, for all x, y ∈ E. The least positive number satisfying this, called the normal constant [1].

The cone P is called regular, if every increasing sequence which is bounded from above is convergent. That is, if {x _n }_n≥1is a sequence such that x₁ ≤ x₂ ≤ ··· ≤ y for some y ∈ E, then there exist x ∈ E such that lim_n→∞||x _n - x|| = 0. Equivalently, the cone P is regular, if and only if, every decreasing sequence which is bounded from below is convergent [1]. Also, every regular cone is normal [5]. Following example shows that the converse is not true.

Example 2.1. [5]Supposewith the norm || f || = || f ||_∞ + || f' ||_∞, and consider the cone P = { f ∈ E : f ≥ 0}. For each K ≥ 1, put f(x) = x and g(x) = x^2K. Then, 0 ≤ g ≤ f, || f || = 2, and ||g|| = 2K + 1. Since K|| f || < ||g||, K is not normal constant of P.

In this paper, E denotes a real Banach space, P denotes a cone in E with intP ≠ ∅ and ≤ denotes partial ordering with respect to P. Let X be a nonempty set. A function d : X × X → E is called a cone metric on X, if it satisfies the following conditions:

(I) d(x, y) ≥ 0 for all x, y ∈ X and d(x, y) = 0, if and only if, x = y,

(II) d(x, y) = d(y, x), for all x, y ∈ X,

(III) d(x, y) ≤ d(x, z) + d(y, z), for all x, y, z ∈ X.

Then, (X, d) is called a cone metric space (see [1]).

Example 2.2. [5]Suppose E = ℓ¹, P = {{x _n }_n∈ℕ∈ E : x _n ≥ 0, for all n} and (X, ρ) be a metric space. Suppose d : X × X → E is defined by. Then, (X, d) is a cone metric space and the normal constant of P is equal to 1.

Example 2.3. Let E = ℝ², P = {(x, y) ∈ E | x, y ≥ 0}, x = ℝ. Suppose d : X × X → E is defined by d(x, y) = (|x - y|, α|x - y|), where α ≥ 0 is a constant. Then, (X, d) is a cone metric space.

The following definitions and lemmas have been chosen from [1].

Definition 2.4. Let (X, d) be a cone metric space and {x _n }_n∈ℕbe a sequence in x and x ∈ X. If for all c ∈ E with 0 ≪ c, there is n₀ ∈ ℕ such that for all n > n₀, d(x _n , x₀) ≪ c, then {x _n }_n∈ℕis said to be convergent and {x _n }_n∈ℕconverges to x and x is the limit of {x _n }_n∈ℕ.

Definition 2.5. Let (X, d) be a cone metric space and {x _n }_n∈ℕbe a sequence in X. If for all c ∈ E with 0 ≪ c, there is n₀ ∈ ℕ such that for all m, n > n₀, d(x _n , x _m ) ≪ c, then {x _n }_n∈ℕis called a Cauchy sequence in X.

Definition 2.6. Let (X, d) be a cone metric space. If every Cauchy sequence is convergent in X, then X is called a complete cone metric space.

Definition 2.7. Let (X, d) be a cone metric space. A self-map T on X is said to be continuous, if lim_n→∞x _n = x implies lim_n→∞T (x _n ) = T (x) for all sequence {x _n }_n∈ℕin X.

We use the following lemmas in the proof of the main result and refer to [1] for their proofs.

Lemma 2.8. Let (X, d) be a cone metric space and P be a cone. Let {x _n }_n∈ℕbe a sequence in X. Then, {x _n }_n∈ℕconverges to x, if and only if,

(2.1)

Lemma 2.9. Let (X, d) be a cone metric space and {x _n }_n∈ℕbe a sequence in X. If {x _n }_n∈ℕis convergent, then it is a Cauchy sequence.

Lemma 2.10. Let (X, d) be a cone metric space and P be a cone in E. Let {x _n }_n∈ℕbe a sequence in X. Then, {x _n }_n∈ℕis a Cauchy sequence, if and only if,

(2.2)

In 1969, Meir and Keeler [4] introduced a new type of fixed point theorem by defining Meir-Keeler contraction (KMC) as a new contractive condition in complete metric spaces. It is as follows:

Theorem 2.11. Let (X, d) be a complete metric space and f has the property (KMC) on X, that is, for all ε > 0, there exists δ > 0 such that

for all x, y ∈ X. Then, f has a unique fixed point.

In 2006, Suzuki [10] proved the integral type contraction (which has been introduced by Branciari [11]) is a special case of KMC (see also[12]). In 2010, Rezapour et al. [13] extended Meir-Keeler's theorem to cone metric spaces as follows:

Theorem 2.12. Let (X, d) be a complete regular cone metric space and f has the property (KMC) on X, that is, for all 0 ≠ ε ∈ P, there exists δ ≫ 0 such that

for all x, y ∈ X. Then, f has a unique fixed point.

3 Cone integration

We recall the following definitions and lemmas of cone integration and refer to [7] for their proofs.

Definition 3.1. Suppose P is a cone in E. Let a, b ∈ E and a < b. Define

(3.1)

and

(3.2)

Definition 3.2. The set {a = x₀, x₁,···, x _n = b} is called a partition for [a, b], if and only if, the intervalsare pairwise disjoint and. Denoteas the collection of all partitions of [a, b].

Definition 3.3. For each partition Q of [a, b] and each increasing function ϕ : [a, b] → E, we define cone lower summation and cone upper summation as

(3.3)

and

(3.4)

respectively. Also, we denote ||Δ(Q)|| = sup{||x _i - x_i-1||, x _i ∈ Q}.

Definition 3.4. Suppose P is a cone in E. ϕ : [a, b] → E is called an integrable function on [a, b] with respect to cone P or to simplicity, cone integrable function, if and only if, for all partition Q of [a, b]

which S^Con must be unique.

We show the common value S ^Con by

We denote the set of all cone integrable function ϕ : [a, b] → E by .

Lemma 3.5. Let M be a subset of P. The following conditions hold:

(1)

(2)

Definition 3.6. The function ϕ : [a, b] → E is called sub-additive cone integrable function, if and only if, for each a, b ∈ P

(3.5)

In 2010, Khojasteh et al. [7] introduced the following fixed point theorem in cone metric spaces.

Theorem 3.7. Let (X, d) be a complete cone metric space and ϕ : P → P be a non-vanishing, sub-additive cone integrable mapping on each [a, b] ⊂ P such that for each ε ≫ 0, and the mapping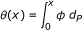for (x ≥ 0), has a continuous inverse at zero. If f : X → X is a mapping such that

for all x, y ∈ X, and for some α ∈ (0, 1). Then, f has a unique fixed point in X.

Also, they proved the following lemma:

Lemma 3.8. Let E = ℝ², P = {(x, y) ∈ E | x, y ≥ 0}, x = ℝ. Suppose d : X × X → E is defined by d(x, y) = (|x - y|, α|x - y|), where α ≥ 0 is a constant. Suppose ϕ : [(0, 0), (a, b)] → P is defined by ϕ(x, y) = (ϕ₁(x), ϕ₂(y)), whereare two integrable functions. Then,

The rest of the paper is organized as follows: In Section 4, we extend Theorems 1.4 and 3.7 in cone metric spaces. Many authors avoid of using the normality condition of P (see [13–15]). Here, we avoid of using such condition and the sub-additivity assumption (Theorem 4.7). In addition, a new generalization of Theorems 1.4 and 3.7 which has a closer relative with KMC (see [4, 10]), is given. In Section 5, an example is given to illustrate our result is a generalization of the results given by Moradi et al. [8] and Khojasteh et al. [7].

4 Some extensions of recent results

The following definitions play a crucial role to state the main results.

Definition 4.1. A mapping F : P → P is said to be right continuous, if for each pair of sequences {x _n } and {y _n } in P, there exist sequences {e _n } and {ε _n } (where, for all n ∈ ℕ), such that

where ε _n → 0 and (x _n - y _n ) → 0, then F (x _n ) - F(y _n ) → 0.

Definition 4.2. A mapping F : P → P is bounded, if for each bounded subset Q ⊂ P with respect to norm of E, F(Q) is a bounded subset.

Definition 4.3. Let P be a cone in E. Let Ω be the set of all mappings F : P → P such that

(I) F^-1(0) = {0}.

(II) For each sequence {t _n } ⊂ P, F (t _n ) → 0 implies that t _n → 0.

(III) F is bounded and non-decreasing in a sense that F(a) ≤ F(b) if a ≤ b, for every a, b ∈ P.

(IV) F be right continuous as declared in Definition 4.1.

Definition 4.4. ψ: P → P is called a-function, if for each ε ≫ 0, there exists δ ≫ 0 such that ψ(t) ≤ ε for each ε ≤ t ≤ ε + δ. Supposedenote the set of all-functions on P into itself.

Example 4.5. For each x ∈ P define ψ(x) = αx, which α ∈ [0, 1). Suppose ε ≫ 0 is given. Takingimplies that ψ(x) ≤ ε for each ε ≤ x ≤ ε + δ. Thus, ψ is a-function.

Definition 4.6. Let (X, d) be a cone metric space and f, T : X → X be two functions and F ∈ Ω. The mapping f is said to be T _F - contraction, if there exists α ∈ [0, 1) such that for all x, y ∈ X,

(4.1)

The following theorem extends the previous result given by Moradi et al. [8] and Khojasteh et al. [7] without assuming to be sub-additive.

Theorem 4.7. Let (X, d) be a complete cone metric space, α ∈ [0, 1) and T, f : X → X be two mappings such that T is one-to-one and closed graph, and f is T _F - contraction, respectively, where F ∈ Ω. Then, f has a unique fixed point a ∈ X. Also, for every x₀ ∈ X, the sequence of iterates {Tfⁿx₀} converges to Ta.

Proof. Uniqueness of the fixed point follows from (4.1). Let x₀ ∈ X, x_n+1= fx _n and y _n = Tx _n for all n ∈ ℕ. We break the argument into four steps.

Step 1.

(4.2)

By using (4.1),

(4.3)

Hence by (4.3),

(4.4)

Since F ∈ Ω,

Step 2. {y _n }is a bounded sequence.

If {y _n } is unbounded, then choose the sequence such that n(1) = 1, n(2) > n(1) is minimal in the sense of e₁ < d(y_n(2), y_n(1)) for some e₁ ∈P, where ||e₁|| = 1. Similarly, n(3) > n(2) is minimal in the sense of e₂< d(y_n(3), y_n(2)) for some e₂ ∈ P, where ||e₂|| = 1,..., n(k + 1) > n(k) is minimal in the sense of

(4.5)

for some e _k ∈ P, where ||e _k || = 1. By Step 1, there exists N₀ ∈ ℕ such that for all k ≥ N₀ we have n(k + 1) - n(k) ≥ 2. Obviously, for every k ≥ N₀ there exists where and

(4.6)

Using (4.5), (4.6) and triangle inequality,

(4.7)

Hence, the sequence {d(y_n(k), y_n(k+1))} is bounded.

If ε _k = d(y_n(k)-1, y_n(k)) + 2d(y_n(k+1), y_n(k+1)-1), then ε _k → 0. Also

(4.8)

In addition,

(4.9)

Since F is right continuous,

(4.10)

From F(d(y_n(k+1), y_n(k))) ≤ αF (d(y_n(k+1)-1, y_n(k)-1)), we conclude

(4.11)

This means that,

(4.12)

Since 1 - α > 0 and (4.10) holds, then F(d(y_n(k)-1, y_n(k+1)-1)) → 0. So from (4.8), e _k → 0 and this is a contradiction because ||e _k || = 1.

Step 3. {y _n } is Cauchy sequence.

Let m, n ∈ ℕ and m > n, from (4.1),

(4.13)

Since {y _n } is bounded and (4.13) holds, . This means that, {y _n } is a Cauchy sequence.

Step 4. f has a fixed point.

Since (X, d) is a complete cone metric space and {y _n } is Cauchy, there exists y ∈ X such that . Since T is closed graph, there exists a ∈ X such that Ta = y. For every n ∈ ℕ

(4.14)

This shows F(d(y_n+1, Tf (a))) → 0. So d(y_n+1, Tf (a)) → 0. Therefore, y _n → Tf(a), i.e., Tf(a) = Ta. Since T is one to one, thus fa = a.□

Lemma 4.8. Define, where ϕ : P → P is a non-vanishing mapping and sub-additive cone integrable on each [a, b] ⊂ P such that for each ε ≫ 0, and the mapping F(x) by (x ≥ 0), has a continuous inverse. Then, F satisfies all conditions of Definition 4.3.

Proof. It suffices to show that F is bounded. Arguing by contradiction, suppose F is unbounded. There exists a sequence {x _k } ⊂ P such that for all k ∈ ℕ, ||x _k || = 1 and ||F(x _k )|| → ∞. We can choose n _k ∈ ℕ and e _k ∈ P such that, ||e _k || = 1 for each k ∈ ℕ and

(4.15)

On the other hand,

(4.16)

Thus

(4.17)

This means that,

(4.18)

If n _k → ∞ then

(4.19)

Suppose a ∈ intP. From we conclude that, there exists M > 0 such that for each k ≥ M, and it means that

(4.20)

Therefore, (4.20) contradicts (4.19).

Remark 4.9. Ifis a non-decreasing function and F(1) ≠ 0, then the condition (II) of Definition 4.3 holds. Indeed, if {t _n } is a sequence insuch that F(t _n ) → 0 and, then there exists ε > 0 and a subsequenceof {t _n } such that. Thus, and this is a contradiction. Therefore,

Suppose P = {(x, y) : x ≥ 0, y ≥ 0} as a cone in ℝ². If one define F : P → P by F(a, b) = (ab, ab), then F is non-decreasing function andbut . This means, such property does not holds in cone metric spaces. In other words, in cone metric spaces

Corollary 4.10. Let (X, d) be a complete cone metric space and P be a cone. Let T : X → X be a mapping such that T is one to one and closed graph. Suppose ϕ : P → P is a non-vanishing mapping and sub-additive cone integrable on each [a, b] ⊂ P such that for each ε ≫ 0, and the mapping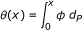, by (x ≥ 0) has a continuous inverse. If f : X → X is a mapping such that for all x, y ∈ X

(4.21)

for some α ∈ (0, 1), then f has a unique fixed point in X.

Proof. Set in Theorem 4.7 and by using Lemma 4.8, the desired result is obtained.

Remark 4.11. Theorem 4.7 is an extension of Theorem 1.4 and 3.7 in cone metric spaces.

Corollary 4.12. Let (X, d) be a complete metric space, α ∈ [0, 1) and T, f : X → X be two mappings such that T is one-to-one and closed graph, and f is T _F -contraction, respectively, where F ∈ Ω. Then, f has a unique fixed point a ∈ X. Also, for every x₀ ∈ X, the sequence of iterates {Tfⁿx₀} converges to Ta.

Proof. By the same proof asserted in Theorem 4.7, the result is obtained.□

The following theorem is a diverse generalization of the results given by Moradi et al. [8], Khojasteh et al. [7], Suzuki [10], Meir-Keeler [4] and Reza-pour et al. [13].

Theorem 4.13. Let (X, d) be a complete regular cone metric space and f be a mapping on X. Let T : X → X be a mapping such that T is one to one and closed graph. Assume that there exists a function θ from P into itself satisfying the following:

(I) θ(0) = 0 and θ(t) ≫ 0 for all t ≫ 0.

(II) θ is non-decreasing and continuous function. Moreover, its inverse is continuous.

(III) For all 0 ≠ ε ∈ P, there exists δ ≫ 0 such that for all x, y ∈ X

(4.22)

(IV) For all x, y ∈ X

(4.23)

Then, f has a unique fixed point.

Proof. θ(d(Tf(x), Tf(y))) < θ(d(Tx, Ty)) for all x, y ∈ X with x ≠ y. If not, there exist x₀, y₀ ∈ X such that

(4.24)

does not holds. Now, choose δ ≫ 0 such that

(4.25)

It means that, θ(d(Tf(x₀), Tf (y₀))) < θ(d(Tf (x₀), Tf (y₀))) and this is a contradiction. Let x₀ ∈ X, x _n = f (x_{n- 1}) and y _n = Tx _n , for all n ∈ ℕ. (If there is a natural m ∈ N such that d(y_m+1, y _m ) = 0, then d(Tx_m+1, Tx _m ) = 0. Since T is one to one, d(x_m+1, x _m ) = 0. Thus, f(x _m ) = x _m and so f has a fixed point). Let d(y_n+1, y _n ) ≠ 0 for all n ∈ ℕ. So θ(d(y_n+1, y _n )) < θ(d(y _n , y_{n- 1})). Hence, according to regularity of P, there exists α ∈ P such that θ(d(y_n+1, y _n )) → α. We claim that α = 0. If α ≠ 0, then according to condition (III), there exists 0 ≪ d such that θ(d(Tf(x), Tf(y)) < α for all x, y ∈ X with θ(d(Tx, Ty)) < α + d. Choose r > 0 such that and take the natural number N such that ||θ(d(y_n+1, y _n )) - α|| < r for all n ≥ N. So for all n ∈ ℕ

(4.26)

and hence

(4.27)

So, θ(d(y_n+1, y _n )) -α ≪ d. Since f has the property (III), θ(d(y_n+2, y_n+1)) < α for all n ≥ N. This is a contradiction because α < θ(d(y_i+1, y _i )) for all i ≥ 1. Thus

(4.28)

is Cauchy sequence. If not, then there is a 0 ≪ c such that for all natural number k, there are m _k , n _k > k so that the relation does not holds. Since θ has continuous inverse, there exists 0 ≪ c such that for all k ∈ ℕ, there are m _k , n _k > k such that the relation does not holds. For 0 ≪ e ≪ c there exists 0 ≪ d such that θ(d(Tf(x), Tf(y))) < e for all x, y ∈ X with θ(d(Tx, Ty)) < e + d. Choose a natural number M such that for all i ≥ M. Also, take m _M ≥ n _M > M such that the relation does not holds. Then, condition (IV) yields

(4.29)

Hence, . Similarly, . Thus,

(4.30)

which is a contradiction. Therefore, is a Cauchy sequence. Since (X, d) is complete, there is u ∈ X such that . Hence, . Since T is closed graph, thus there exists v ∈ X such that Tv = u. Now,

(4.31)

Therefore, y_n+1= Tx_n+1→Tfv. Hence, Tfv = Tv. Since T is one to one we conclude that fv = v. Hence, f has a fixed point. Uniqueness of the fixed point follows from

(4.32)

for all x ≠ y.

Remark 4.14. The following notations are considerable:

• By taking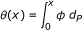in Theorem 4.13, where ϕ satisfies the assumptions of Corollary 4.10, Corollary 4.10 is concluded.

• By taking Tx ≡ x in Corollary 4.10, Khojasteh's result is concluded.

• By taking Tx ≡ x in Theorem 4.13, Suzuki[10] and Rezapour-Haghi's results [13], are concluded.

The following theorem is a direct result of Theorem 4.13.

Theorem 4.15. Let (X, d) be a complete cone metric space, α ∈ [0, 1) and T, f : X → X be two mappings such that T is one-to-one and closed graph, and f satisfies

(4.33)

for all x, y ∈ X, respectively, where θ : P → P satisfies in (I), (II) and (IV) of Theorem 4.13 and(see Definition 4.4). Then, f has a unique fixed point a ∈ X.

Proof. Suppose ε ≫ 0 is given. For each x, y ∈ X, we can choose δ ≫ 0 such that ε ≤ θ(d(Tx, Ty)) ≤ ε + δ. Since ψ is a L-function thus we have

(4.34)

This means that, the condition (III) of Theorem 4.13 holds and so f has a unique fixed point.□

Corollary 4.16. Let (X, d) be a complete metric space, α ∈ [0, 1) and T, f : X → X be two mappings such that T is one-to-one and closed graph, and f satisfies

(4.35)

for all x, y ∈ X, respectively, where ψ is a-function andis a non-vanishing integrable mapping on eachsuch that for each ε > 0, . Then, f has a unique fixed point a∈ X.

Proof. By taking and in Theorem 4.15, the desired result is obtained.

5 An example

In this section, we give an example to illustrate our results.

Example 5.1. Let , E = ℝ² and P = {(x, y) ∈ E : x, y ≥ 0}. Suppose d(x, y) = (|x - y|, |x - y|), for each x, y ∈ X. Then, (X, d) is a complete cone metric space. Let f : X → X be defined by

(5.1)

It is easy to see that f has a unique fixed point x = 0. Let be defined by

(5.2)

It is easy to compute that,

This implies that has the continuous inverse at zero. Consider the mapping ϕ : P → E defined by

Since has the continuous inverse on by Lemma 3.8, we deduce

has the continuous inverse at zero. We show, f does not satisfy in Theorem 3.7 with ϕ defined as above.

Indeed, for , (m > n are even) and using Lemma 3.8, we have

(5.3)

and

(5.4)

Now, if

for some q ∈ [0, 1). Then, by taking n = 2 and m = 4, we get

This means that, q > 1 and this is a contradiction. Therefore, we can't apply Theorem 3.7 for f.

But we claim, f satisfies in Corollary 4.10 by the same ϕ. If we define T by

(5.5)

Obviously, T is one to one, continuous and closed graph. It is easy to see,

(5.6)

We claim that,

To prove our claim we need to consider the following cases:

Case (1). If and (m > n are even), then

iff

iff

It is easy to see that, the last inequality is equivalent to

From

we deduce

Also, since and we have

Thus, the desired result is obtained.

Case (2). If and , where m, n are odd.

Case (3). If and , where m is odd and n is even.

Proof of the Case (2) and (3) are similar to the argument as in the Case (1).

Case (4). If x = 0 and , such that n is even, then

iff

iff

iff

From and , the desired result is obtained.

Case (5). If x = 0 and , such that n is odd, then

iff

iff

iff

From and , the desired result is obtained. Therefore, one can apply Theorem 4.10 for the mapping f.

Remark 5.2. Example 5.1 shows Corollary 4.10 is an extension of Theorem 3.7.