- Research
- Open access
- Published:
Strong convergence theorems for system of equilibrium problems and asymptotically strict pseudocontractions in the intermediate sense
Fixed Point Theory and Applications volume 2011, Article number: 13 (2011)
Abstract
Let  be N uniformly continuous asymptotically λ
i
-strict pseudocontractions in the intermediate sense defined on a nonempty closed convex subset C of a real Hilbert space H. Consider the problem of finding a common element of the fixed point set of these mappings and the solution set of a system of equilibrium problems by using hybrid method. In this paper, we propose new iterative schemes for solving this problem and prove these schemes converge strongly.
be N uniformly continuous asymptotically λ
i
-strict pseudocontractions in the intermediate sense defined on a nonempty closed convex subset C of a real Hilbert space H. Consider the problem of finding a common element of the fixed point set of these mappings and the solution set of a system of equilibrium problems by using hybrid method. In this paper, we propose new iterative schemes for solving this problem and prove these schemes converge strongly.
MSC: 47H05; 47H09; 47H10.
1. Introduction
Let H be a real Hilbert space and let C be a nonempty closed convex subset of H.
A nonlinear mapping S : C → C is a self mapping of C. We denote the set of fixed points of S by F(S) (i.e., F(S) = {x ∈ C : Sx = x}). Recall the following concepts.
-
(1)
S is uniformly Lipschitzian if there exists a constant L > 0 such that
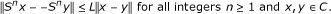
-
(2)
S is nonexpansive if
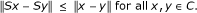
-
(3)
S is asymptotically nonexpansive if there exists a sequence k n of positive numbers satisfying the property limn→∞ k n = 1 and

-
(4)
S is asymptotically nonexpansive in the intermediate sense [1] provided S is continuous and the following inequality holds:

-
(5)
S is asymptotically λ-strict pseudocontractive mapping [2] with sequence {γ n } if there exists a constant λ ∈ [0, 1) and a sequence {γ n } in [0, ∞) with limn→∞ γ n = 0 such that

for all x, y ∈ C and n ∈ ℕ.
-
(6)
S is asymptotically λ-strict pseudocontractive mapping in the intermediate sense [3, 4] with sequence {γ n } if there exists a constant λ ∈ [0, 1) and a sequence {γ n } in [0, ∞) with limn→∞ γ n = 0 such that
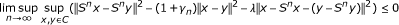 (1.1)
(1.1)
for all x, y ∈ C and n ∈ ℕ.
Throughout this paper, we assume that

Then, c n ≥ 0 for all n ∈ N, c n → 0 as n → ∞ and (1.1) reduces to the relation

for all x, y ∈ C and n ∈ ℕ.
When c n = 0 for all n ∈ N in (1.2), then S is an asymptotically λ-strict pseudocontractive mapping with sequence {γ n }. We note that S is not necessarily uniformly L-Lipschitzian (see [4]), more examples can also be seen in [3].
Let {F k } be a countable family of bifunctions from C × C to ℝ, where ℝ is the set of real numbers. Combettes and Hirstoaga [5] considered the following system of equilibrium problems:

where Γ is an arbitrary index set. If Γ is a singleton, then problem (1.3) becomes the following equilibrium problem:

The solution set of (1.4) is denoted by EP(F).
The problem (1.3) is very general in the sense that it includes, as special cases, optimization problems, variational inequalities, minimax problems, Nash equilibrium problem in noncooperative games and others; see, for instance, [6, 7] and the references therein. Some methods have been proposed to solve the equilibrium problem (1.3), related work can also be found in [8–11].
For solving the equilibrium problem, let us assume that the bifunction F satisfies the following conditions:
(A1) F(x, x) = 0 for all x ∈ C;
(A2) F is monotone, i.e.F(x, y) + F(y, x) ≤ 0 for any x, y ∈ C;
(A3) for each x, y, z ∈ C, lim supt→0F(tz + (1 - t)x, y) ≤ F(x, y);
(A4) F(x,·) is convex and lower semicontionuous for each x ∈ C.
Recall Mann's iteration algorithm was introduced by Mann [12]. Since then, the construction of fixed points for nonexpansive mappings and asymptotically strict pseudocontractions via Mann' iteration algorithm has been extensively investigated by many authors (see, e.g., [2, 6]).
Mann's iteration algorithm generates a sequence {x n } by the following manner:

where α n is a real sequence in (0, 1) which satisfies certain control conditions.
On the other hand, Qin et al. [13] introduced the following algorithm for a finite family of asymptotically λ
i
-strict pseudocontractions. Let x0 ∈ C and  be a sequence in (0, 1). The sequence {x
n
} by the following way:
be a sequence in (0, 1). The sequence {x
n
} by the following way:

It is called the explicit iterative sequence of a finite family of asymptotically λ i -strict pseudocontractions {S1, S2,..., S N }. Since, for each n ≥ 1, it can be written as n = (h - 1)N + i, where i = i(n) ∈ {1, 2,..., N}, h = h(n) ≥ 1 is a positive integer and h(n) → ∞, as n → ∞. We can rewrite the above table in the following compact form:

Recently, Sahu et al. [4] introduced new iterative schemes for asymptotically strict pseudocontractive mappings in the intermediate sense. To be more precise, they proved the following theorem.
Theorem 1.1. Let C be a nonempty closed convex subset of a real Hilbert space H and T: C → C a uniformly continuous asymptotically κ-strict pseudocontractive mapping in the intermediate sense with sequence γ n such that F(T) is nonempty and bounded. Let α n be a sequence in [0, 1] such that 0 < δ ≤ α n ≤ 1 - κ for all n ∈ N. Let {x n } ⊂ C be sequences generated by the following (CQ) algorithm:

where θ n = c n + γ n Δ n and Δ n = sup {||x n - z||: z ∈ F(T)} < ∞. Then, {x n } converges strongly to PF(T)(u).
Very recently, Hu and Cai [3] further considered the asymptotically strict pseudocontractive mappings in the intermediate sense concerning equilibrium problem. They obtained the following result in a real Hilbert space.
Theorem 1.2. Let C be a nonempty closed convex subset of a real Hilbert space H and N ≥ 1 be an integer, ϕ : C → C be a bifunction satisfying (A1)-(A4) and A : C → H be an α-inverse-strongly monotone mapping. Let for each 1 ≤ i ≤ N, T
i
: C → C be a uniformly continuous k
i
-strictly asymptotically pseudocontractive mapping in the intermediate sense for some 0 ≤ k
i
< 1 with sequences {γ
n,i
} ⊂ [0, ∞) such that limn→∞γ
n,i
= 0 and {c
n,i
} ⊂ [0, ∞) such that limn→∞c
n,i
= 0. Let k = max{k
i
: 1 ≤ i ≤ N}, γ
n
= max{γ
n,i
: 1 ≤ i ≤ N} and c
n
= max{c
n,i
: 1 ≤ i ≤ N}. Assume that is nonempty and bounded. Let {α
n
} and {β
n
} be sequences in [0, 1] such that 0 < a ≤ α
n
≤ 1, 0 < δ ≤ β
n
≤ 1 - k for all n ∈ N and 0 < b ≤ r
n
≤ c < 2α. Let {x
n
} and {u
n
} be sequences generated by the following algorithm:
is nonempty and bounded. Let {α
n
} and {β
n
} be sequences in [0, 1] such that 0 < a ≤ α
n
≤ 1, 0 < δ ≤ β
n
≤ 1 - k for all n ∈ N and 0 < b ≤ r
n
≤ c < 2α. Let {x
n
} and {u
n
} be sequences generated by the following algorithm:

where , as n → ∞, where ρ
n
= sup{||x
n
- v||: v ∈ F} < ∞. Then, {x
n
} converges strongly to PF(T)x0.
, as n → ∞, where ρ
n
= sup{||x
n
- v||: v ∈ F} < ∞. Then, {x
n
} converges strongly to PF(T)x0.
Motivated by Hu and Cai [3], Sahu et al. [4], and Duan [8], the main purpose of this paper is to introduce a new iterative process for finding a common element of the fixed point set of a finite family of asymptotically λ i -strict pseudocontractions and the solution set of the problem (1.3). Using the hybrid method, we obtain strong convergence theorems that extend and improve the corresponding results [3, 4, 13, 14].
We will adopt the following notations:
-
1.
⇀ for the weak convergence and → for the strong convergence.
-
2.
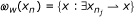 denotes the weak ω-limit set of {x
n
}.
denotes the weak ω-limit set of {x
n
}.
2. Preliminaries
We need some facts and tools in a real Hilbert space H which are listed below.
Lemma 2.1. Let H be a real Hilbert space. Then, the following identities hold.
(i) ||x - y||2 = ||x||2 - ||y||2 - 2〈x - y, y〉, ∀x, y ∈ H.
(ii) ||tx +(1 - t)y||2 = t||x||2+(1 - t)||y||2 - t(1 - t)||x - y||2, ∀t ∈ [0, 1], ∀x, y ∈ H.
Lemma 2.2. ([10]) Let H be a real Hilbert space. Given a nonempty closed convex subset C ⊂ H and points x, y, z ∈ H and given also a real number a ∈ ℝ, the set

is convex (and closed).
Lemma 2.3. ([15]) Let C be a nonempty, closed and convex subset of H. Let {x n } be a sequence in H and u ∈ H. Let q = P C u. Suppose that {x n } is such that ω w (x n ) ⊂ C and satisfies the following condition

Then, x n → q.
Lemma 2.4. ([4]) Let C be a nonempty closed convex subset of a real Hilbert space H and T : C → C a continuous asymptotically κ-strict pseudocontractive mapping in the intermediate sense. Then I - T is demiclosed at zero in the sense that if {x n } is a sequence in C such that x n ⇀ x ∈ C and lim supm→∞lim supn→∞||x n - Tmx n || = 0, then (I - T)x = 0.
Lemma 2.5. ([4]) Let C be a nonempty subset of a Hilbert space H and T : C → C an asymptotically κ - strict pseudocontractive mapping in the intermediate sense with sequence {γ n }. Then

for all x, y ∈ C and n ∈ N.
Lemma 2.6. ([6]) Let C be a nonempty closed convex subset of H, let F be bifunction from C × C to ℝ satisfying (A1)-(A4) and let r > 0 and x ∈ H. Then there exists z ∈ C such that

Lemma 2.7. ([5]) For r > 0, x ∈ H, define a mapping T r : H → C as follows:

for all x ∈ H. Then, the following statements hold:
-
(i)
T r is single-valued;
-
(ii)
T r is firmly nonexpansive, i.e., for any x, y ∈ H,
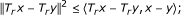
-
(iii)
F(T r ) = EP(F);
-
(iv)
EP(F) is closed and convex.
3. Main result
Theorem 3.1. Let C be a nonempty closed convex subset of a real Hilbert space H and N ≥ 1 be an integer, let F
k
, k ∈ {1, 2, ... M}, be a bifunction from C × C to ℝ which satisfies conditions (A1)-(A4). Let, for each 1 ≤ i ≤ N, S
i
: C → C be a uniformly continuous asymptotically λ
i
-strict pseudocontractive mapping in the intermediate sense for some 0 ≤ λ
i
< 1 with sequences {γ
n,i
} ⊂ [0, ∞) such that limn→∞γ
n,i
= 0 and {c
n,i
} ⊂ [0, ∞) such that limn→∞c
n,i
= 0. Let λ = max{λ
i
: 1 ≤ i ≤ N}, γ
n
= max{γ
n,i
: 1 ≤ i ≤ N} and c
n
= max{c
n,i
: 1 ≤ i ≤ N}. Assume that is nonempty and bounded. Let {α
n
} and {β
n
} be sequences in [0, 1] such that 0 < a ≤ α
n
≤ 1, 0 < δ ≤ β
n
≤ 1 - λ for all n ∈ ℕ and {r
k,n
} ⊂ (0, ∞) satisfies lim infn→∞r
k,n
> 0 for all k ∈ {1, 2, ... M}. Let {x
n
} and {u
n
} be sequences generated by the following algorithm:
is nonempty and bounded. Let {α
n
} and {β
n
} be sequences in [0, 1] such that 0 < a ≤ α
n
≤ 1, 0 < δ ≤ β
n
≤ 1 - λ for all n ∈ ℕ and {r
k,n
} ⊂ (0, ∞) satisfies lim infn→∞r
k,n
> 0 for all k ∈ {1, 2, ... M}. Let {x
n
} and {u
n
} be sequences generated by the following algorithm:

where  , as n → ∞, where ρ
n
= sup{||x
n
- v|| : v ∈ Ω} < ∞. Then {x
n
} converges strongly to PΩx1.
, as n → ∞, where ρ
n
= sup{||x
n
- v|| : v ∈ Ω} < ∞. Then {x
n
} converges strongly to PΩx1.
Proof. Denote  for every k ∈ {1, 2,..., M} and
for every k ∈ {1, 2,..., M} and  for all n ∈ ℕ. Therefore
for all n ∈ ℕ. Therefore  . The proof is divided into six steps.
. The proof is divided into six steps.
Step 1. The sequence {x n } is well defined.
It is obvious that C n is closed and Q n is closed and convex for every n ∈ ℕ. From Lemma 2.2, we also get that C n is convex.
Take p ∈ Ω, since for each k ∈ {1, 2,..., M},  is nonexpansive,
is nonexpansive,  and
and  , we have
, we have

It follows from the definition of S i and Lemma 2.1(ii), we get

By virtue of the convexity of ||·||2, one has

Substituting (3.2) and (3.3) into (3.4), we obtain

It follows that p ∈ C n for all n ∈ ℕ. Thus, Ω ⊂ C n .
Next, we prove that Ω ⊂ Q
n
for all n ∈ ℕ by induction. For n = 1, we have Ω ⊂ C = Q1. Assume that Ω ⊂ Q
n
for some n ≥ 1. Since  , we obtain
, we obtain

As Ω ⊂ C n ⋂ Q n by induction assumption, the inequality holds, in particular, for all z ∈ Ω. This together with the definition of Qn+1implies that Ω ⊂ Qn +1.
Hence Ω ⊂ Q n holds for all n ≥ 1. Thus Ω ⊂ C n ⋂ Q n and therefore the sequence {x n } is well defined.
Step 2. Set q = PΩx1, then

Since Ω is a nonempty closed convex subset of H, there exists a unique q ∈ Ω such that q = PΩx1.
From  , we have
, we have

Since q ∈ Ω ⊂ C n ⋂ Q n , we get (3.6).
Therefore, {x n } is bounded. So are {u n } and {y n }.
Step 3. The following limits hold:

From the definition of Q
n
, we have  , which together with the fact that xn+1∈ C
n
⋂ Q
n
⊂ Q
n
implies that
, which together with the fact that xn+1∈ C
n
⋂ Q
n
⊂ Q
n
implies that

This shows that the sequence {||x n - x1||} is nondecreasing. Since {x n } is bounded, the limit of {||x n - x1||} exists.
It follows from Lemma 2.1(i) and (3.7) that

Noting that limn→∞||x n - x1|| exists, this implies

It is easy to get

Since xn+1∈ C n , we have

So, we get limn→∞||y n - xn+1|| = 0. It follows that

Next we will show that

Indeed, for p ∈ Ω, it follows from the firmly nonexpansivity of  that for each k ∈ {1, 2,..., M}, we have
that for each k ∈ {1, 2,..., M}, we have

Thus we get

which implies that for each k ∈ {1, 2,..., M},

Therefore, by the convexity of ||·||2, (3.5) and the nonexpansivity of  , we get
, we get

It follows that

From (3.10) and (3.13), we obtain (3.11). Then, we have

Combining (3.8) and (3.14), we have

It follows that

Step 4. Show that ||u n - S i u n || → 0, ||x n - S i x n || → 0, as n → ∞; ∀i ∈ {1, 2,..., N}.
Since, for any positive integer n ≥ N, it can be written as n = (h(n) - 1) N + i(n), where i(n) ∈ {1, 2,..., N}. Observe that

From (3.10), (3.14), the conditions 0 < a ≤ α n ≤ 1 and 0 < δ ≤ β n ≤ 1 - λ, we obtain

Next, we prove that

It is obvious that the relations hold: h(n) = h(n - N) + 1, i(n) = i(n - N).
Therefore,

Applying Lemma 2.5 and (3.16), we get (3.19). Using the uniformly continuity of S i , we obtain

this together with (3.17) yields

We also have

for any i = 1, 2, ... N, which gives that

Moreover, for each i ∈ {1, 2, ... N}, we obtain that

Step 5. The following implication holds:

We first show that  . To this end, we take ω ∈ ω
w
(x
n
) and assume that
. To this end, we take ω ∈ ω
w
(x
n
) and assume that  as j → ∞ for some subsequence
as j → ∞ for some subsequence  of x
n
.
of x
n
.
Note that S
i
is uniformly continuous and (3.23), we see that  , for all m ∈ ℕ. So by Lemma 2.4, it follows that
, for all m ∈ ℕ. So by Lemma 2.4, it follows that  and hence
and hence  .
.
Next we will show that  . Indeed, by Lemma 2.6, we have that for each k = 1, 2, ..., M,
. Indeed, by Lemma 2.6, we have that for each k = 1, 2, ..., M,

From (A2), we get

Hence,

From (3.11), we obtain that  as j → ∞ for each k = 1, 2, ..., M (especially,
as j → ∞ for each k = 1, 2, ..., M (especially,  ). Together with (3.11) and (A4) we have, for each k = 1, 2, ..., M, that
). Together with (3.11) and (A4) we have, for each k = 1, 2, ..., M, that

For any, 0 < t ≤ 1 and y ∈ C, let y t = ty + (1 - t)ω. Since y ∈ C and ω ∈ C, we obtain that y t ∈ C and hence F k (y t , ω) ≤ 0. So, we have

Dividing by t, we get, for each k = 1, 2, ..., M, that

Letting t → 0 and from (A3), we get

for all y ∈ C and ω ∈ EP(F
k
) for each k = 1, 2, ..., M, i.e.,  .
.
Hence (3.24) holds.
Step 6. Show that x n → q = PΩx1.
From (3.6), (3.24) and Lemma 2.3, we conclude that x n → q, where q = PΩx1. □
Corollary 3.2. Let C be a nonempty closed convex subset of a real Hilbert space H and N ≥ 1 be an integer, let F be a bifunction from C × C to ℝ which satisfies conditions (A1)-(A4). Let, for each 1 ≤ i ≤ N, S
i
: C → C be a uniformly continuous λ
i
-strict asymptotically pseudocontractive mapping in the intermediate sense for some 0 ≤ λ
i
< 1 with sequences {γn,i} ⊂ [0, ∞) such that limn→∞γn,i= 0 and {cn,i} ⊂ [0, ∞) such that limn→∞c
n
,
i
= 0. Let λ = max{λ
i
: 1 ≤ i ≤ N}, γ
n
= max{γn,i: 1 ≤ i ≤ N} and c
n
= max{cn,i: 1 ≤ i ≤ N}. Assume that is nonempty and bounded. Let {α
n
} and {β
n
} be sequences in [0, 1] such that 0 < a ≤ α
n
≤ 1,0 < δ ≤ β
n
≤ 1 - λ for all n ∈ N and {r
n
} ⊂ (0,∞) satisfies lim infn→∞r
n
> 0 for all k ∈ {1, 2, ... M}.
is nonempty and bounded. Let {α
n
} and {β
n
} be sequences in [0, 1] such that 0 < a ≤ α
n
≤ 1,0 < δ ≤ β
n
≤ 1 - λ for all n ∈ N and {r
n
} ⊂ (0,∞) satisfies lim infn→∞r
n
> 0 for all k ∈ {1, 2, ... M}.
Let {x n } and {u n } be sequences generated by the following algorithm:

where , as n → ∞, where ρ
n
= sup{||x
n
- v|| : v ∈ Ω} < ∞. Then {x
n
} converges strongly to PΩx1.
, as n → ∞, where ρ
n
= sup{||x
n
- v|| : v ∈ Ω} < ∞. Then {x
n
} converges strongly to PΩx1.
Proof. Putting M = 1, we can draw the desired conclusion from Theorem 3.1.
□
Remark 3.3. Corollary 3.2 extends the theorem of Tada and Takahashi [14] from a nonexpansive mapping to a finite family of asymptotically λ i -strict pseudocontractive mappings in the intermediate sense.
Corollary 3.4. Let C be a nonempty closed convex subset of a real Hilbert space H and N ≥ 1 be an integer, let, for each 1 ≤ i ≤ N, S
i
: C → C be a uniformly continuous λ
i
-strict asymptotically pseudocontractive mapping in the intermediate sense for some 0 ≤ λ
i
< 1 with sequences {γn,i} ⊂ [0, ∞) such that limn→∞γn,i= 0 and {c
n,i
} ⊂ [0, ∞) such that limn→∞c
n,i
= 0. Let λ= max{λ
i
: 1 ≤ i ≤ N}, γ
n
= max{γn,i: 1 ≤ i ≤ N} and c
n
= max{c
n,i
: 1 ≤ i ≤ N}. Assume that is nonempty and bounded. Let {α
n
} and {β
n
} be sequences in [0, 1] such that 0 < a ≤ α
n
≤ 1, 0 <δ ≤ β
n
≤ 1 - λ for all n ∈ ℕ. Let {x
n
} and {u
n
} be sequences generated by the following algorithm:
is nonempty and bounded. Let {α
n
} and {β
n
} be sequences in [0, 1] such that 0 < a ≤ α
n
≤ 1, 0 <δ ≤ β
n
≤ 1 - λ for all n ∈ ℕ. Let {x
n
} and {u
n
} be sequences generated by the following algorithm:

where , as n → ∞, where ρ
n
= sup{||x
n
- v|| : v ∈ Ω} < ∞. Then {x
n
} converges strongly to PΩx1.
, as n → ∞, where ρ
n
= sup{||x
n
- v|| : v ∈ Ω} < ∞. Then {x
n
} converges strongly to PΩx1.
Proof. If F k (x, y) = 0, α n = 1 in Theorem 3.1, we can draw the conclusion easily. □
Remark 3.5. Corollary 3.4 extends the Theorem 4.1 of [4] and Theorem 2.2 of [13], respectively.
4. Numerical result
In this section, in order to demonstrate the effectiveness, realization and convergence of the algorithm in Theorem 3.1, we consider the following simple example ever appeared in the reference [4]:
Example 4.1. Let x = R and C = [0, 1] For each x ∈ C, we define

where 0 < k < 1.
Set C1 : = [0, 1/2] and C2 : = (1/2, 1]. Hence,

and

For x ∈ C1 and y ∈ C2, we have

Thus

for all x, y ∈ C, n ∈ ℕ and some K > 0. Therefore, T is an asymptotically k-strict pseudocontractive mapping in the intermediate sense.
In the algorithm (3.1), set  . We apply it to find the fixed point of T of Example 4.1.
. We apply it to find the fixed point of T of Example 4.1.
Under the above assumptions, (3.1) is simplified as follows:

In fact, in one dimensional case, the C n ⋂ Q n is an closed interval. If we set [a n , b n ] := C n ⋂ Q n , then the projection point xn+1of x1 ∈ C onto C n ⋂ Q n can be expressed as:

Since the conditions of Theorem 3.1 are satisfied in Example 4.1, the conclusion holds, i.e., x n → 0 ∈ F (T).
Now we turn to realizing (3.1) for approximating a fixed point of T. Take the initial guess x1 = 1/2, 1/5 and 5/8, respectively. All the numerical results are given in Tables 1, 2 and 3. The corresponding graph appears in Figure 1a,b,c.

References
Bruck RE, Kuczumow T, Reich S: Convergence of iterates of asymptotically nonexpansive mappings in Banach spaces with the uniform opial property. Colloq Math 1993, 65: 169–179.
Kim TH, Xu HK: Convergence of the modified Mann's iteration method for asymptotically strict pseudocontractions. Nonlinear Anal 2008, 68: 2828–2836. 10.1016/j.na.2007.02.029
Hu CS, Cai G: Convergence theorems for equilibrium problems and fixed point problems of a finite family of asymptotically k -strict pseudocontractive mappings in the intermediate sense. Comput Math Appl 2010.
Sahu DR, Xu HK, Yao JC: Asymptotically strict pseudocontractive mappings in the intermediate sense. Nonlinear Anal 2009, 70: 3502–3511. 10.1016/j.na.2008.07.007
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. J Nonlinear Convex Anal 2005, 6: 117–136.
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. Math Stud 1994, 63: 123–145.
Colao V, Marino G, Xu HK: An iterative method for finding common solutions of equilibrium and fixed point problems. J Math Anal Appl 2008, 344: 340–352. 10.1016/j.jmaa.2008.02.041
Duan PC: Convergence theorems concerning hybrid methods for strict pseudocontractions and systems of equilibrium problems. J Inequal Appl 2010.
Flam SD, Antipin AS: Equilibrium programming using proximal-like algorithms. Math Program 1997, 78: 29–41.
Marino G, Xu HK: Weak and srong convergence theorems for strict pseudo-contractions in Hlibert spaces. J Math Anal Appl 2007, 329: 336–346. 10.1016/j.jmaa.2006.06.055
Takahashi S, Takahashi W: Strong convergence theorems for a generalized equilibrium problems and a nonexpansive mapping in a Hlibert space. Nonlinear Anal 2008, 69: 1025–1033. 10.1016/j.na.2008.02.042
Mann WR: Mean value methods in iteration. Proc Am Math Soc 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Qin XL, Cho YJ, Kang SM, Shang M: A hybrid iterative scheme for asymptotically k -strictly pseudocontractions in Hlibert spaces. Nonlinear Anal 2009, 70: 1902–1911. 10.1016/j.na.2008.02.090
Tada A, Takahashi W: Weak and strong convergence theorems for a nonexpansive mappingand a equilibrium problem. J Optim Theory Appl 2007, 133: 359–370. 10.1007/s10957-007-9187-z
Matinez-Yanes C, Xu HK: Srong convergence of the CQ method for fixed point processes. Nonlinear Anal 2006, 64: 2400–2411. 10.1016/j.na.2005.08.018
Acknowledgements
The authors would like to thank the reviewers for their good suggestions. This research is supported by Fundamental Research Funds for the Central Universities (ZXH2011C002).
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors' contributions
PD carried out the proof of convergence of the theorems and realization of numerical examples. JZ carried out the check of the manuscript. All authors read and approved the final manuscript.
Authors’ original submitted files for images
Below are the links to the authors’ original submitted files for images.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Duan, P., Zhao, J. Strong convergence theorems for system of equilibrium problems and asymptotically strict pseudocontractions in the intermediate sense. Fixed Point Theory Appl 2011, 13 (2011). https://doi.org/10.1186/1687-1812-2011-13
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-13
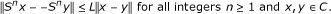
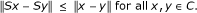



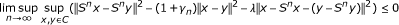
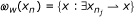 denotes the weak ω-limit set of {x
n
}.
denotes the weak ω-limit set of {x
n
}.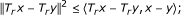

 .
.