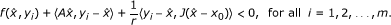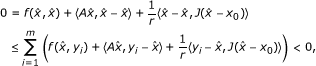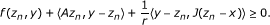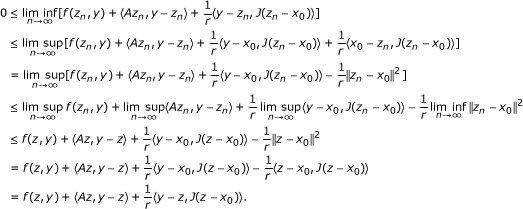- Research
- Open access
- Published:
Existence and iterative approximation for generalized equilibrium problems for a countable family of nonexpansive mappings in banach spaces
Fixed Point Theory and Applications volume 2011, Article number: 11 (2011)
Abstract
We first prove the existence of a solution of the generalized equilibrium problem (GEP) using the KKM mapping in a Banach space setting. Then, by virtue of this result, we construct a hybrid algorithm for finding a common element in the solution set of a GEP and the fixed point set of countable family of nonexpansive mappings in the frameworks of Banach spaces. By means of a projection technique, we also prove that the sequences generated by the hybrid algorithm converge strongly to a common element in the solution set of GEP and common fixed point set of nonexpansive mappings.
AMS Subject Classification: 47H09, 47H10
1. Introduction
Let E be a real Banach space with the dual E* and C be a nonempty closed convex subset of E. We denote by  and
and  the sets of positive integers and real numbers, respectively. Also, we denote by J the normalized duality mapping from E to 2E*defined by
the sets of positive integers and real numbers, respectively. Also, we denote by J the normalized duality mapping from E to 2E*defined by

where 〈·,·〉 denotes the generalized duality pairing. We know that if E is smooth, then J is single-valued and if E is uniformly smooth, then J is uniformly norm-to-norm continuous on bounded subsets of E. We shall still denote by J the single-valued duality mapping. Let  be a bifunction and A : C → E* be a nonlinear mapping. We consider the following generalized equilibrium problem (GEP):
be a bifunction and A : C → E* be a nonlinear mapping. We consider the following generalized equilibrium problem (GEP):

The set of such u ∈ C is denoted by GEP (f), i.e.,

Whenever E = H a Hilbert space, the problem (1.1) was introduced and studied by Takahashi and Takahashi [1]. Similar problems have been studied extensively recently. In the case of A ≡ 0, GEP (f) is denoted by EP (f). In the case of f ≡ 0, EP is also denoted by VI(C, A). Problem (1.1) is very general in the sense that it includes, as spacial cases, optimization problems, variational inequalities, minimax problems, the Nash equilibrium problem in noncooperative games, and others; see, e.g., [2, 3]. A mapping T : C → E is called nonexpansive if ||Tx - Ty|| ≤ ||x - y|| for all x, y ∈ C. Denote by F (T ) the set of fixed points of T , that is, F (T ) = {x ∈ C : Tx = x}. A mapping A : C → E* is called α-inverse-strongly monotone, if there exists an α > 0 such that

It is easy to see that if A : C → E* is an α-inverse-strongly monotone mapping, then it is 1/α- Lipschitzian.
In 1953, Mann [4] introduced the following iterative procedure to approximate a fixed point of a nonexpansive mapping T in a Hilbert space H:

where the initial point x0 is taken in C arbitrarily and {α n } is a sequence in [0, 1].
However, we note that Manns iteration process (1.2) has only weak convergence, in general; for instance, see [5–7].
Let C be a nonempty, closed, and convex subset of a Banach space E and {T
n
} be sequence of mappings of C into itself such that  . Then, {T
n
} is said to satisfy the NST-condition if for each bounded sequence {z
n
} ⊂ C,
. Then, {T
n
} is said to satisfy the NST-condition if for each bounded sequence {z
n
} ⊂ C,

implies  , where ω
w
(z
n
) is the set of all weak cluster points of {z
n
}; see [8–10].
, where ω
w
(z
n
) is the set of all weak cluster points of {z
n
}; see [8–10].
In 2008, Takahashi et al. [11] has adapted Nakajo and Takahashi's [12] idea to modify the process (1.2) so that strong convergence has been guaranteed. They proposed the following modification for a family of nonexpansive mappings in a Hilbert space: x0 ∈ H, C1 = C,  and
and

where 0 ≤ α
n
≤ a < 1 for all 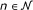 . They proved that if {T
n
} satisfies the NST-condition, then {u
n
} generated by (1.3) converges strongly to a common fixed point of T
n
.
. They proved that if {T
n
} satisfies the NST-condition, then {u
n
} generated by (1.3) converges strongly to a common fixed point of T
n
.
Recently, motivated by Nakajo and Takahashi [12] and Xu [13], Matsushita and Takahashi [14] introduced the iterative algorithm for finding fixed points of nonexpansive mappings in a uniformly convex and smooth Banach space: x0 = x ∈ C and

where  denotes the convex closure of the set D, {t
n
} is a sequence in (0,1) with t
n
→ 0, and
denotes the convex closure of the set D, {t
n
} is a sequence in (0,1) with t
n
→ 0, and  is the metric projection from E onto C
n
∩ D
n
. They proved that {x
n
} generated by (1.4) converges strongly to a fixed point of T .
is the metric projection from E onto C
n
∩ D
n
. They proved that {x
n
} generated by (1.4) converges strongly to a fixed point of T .
Very recently, Kimura and Nakajo [15] investigated iterative schemes for finding common fixed points of a family of nonexpansive mappings and proved strong convergence theorems by using the Mosco convergence technique in a uniformly convex and smooth Banach space. In particular, they proposed the following algorithm: x1 = x ∈ C and

where {t n } is a sequence in (0,1) with t n → 0 as n → ∞. They proved that if {T n } satisfies the NST-condition, then {x n } converges strongly to a common fixed point of T n .
Motivated and inspired by Nakajo and Takahashi [12], Takahashi et al. [11], Xu [13], Masushita and Takahashi [14], and Kimura and Nakajo [15], we introduce a hybrid projection algorithm for finding a common element in the solution set of a GEP and the common fixed point set of a family of nonexpansive mappings in a Banach space setting.
2. Preliminaries
Let E be a real Banach space and let U = {x ∈ E : ||x|| = 1} be the unit sphere of E. A Banach space E is said to be strictly convex if for any x, y ∈ U,

It is also said to be uniformly convex if for each ε ∈ (0, 2], there exists δ > 0 such that for any x, y ∈ U,

It is known that a uniformly convex Banach space is reflexive and strictly convex. Define a function δ: [0, 2] → [0, 1] called the modulus of convexity of E as follows:

Then, E is uniformly convex if and only if δ(ε) > 0 for all ε ∈ (0, 2]. A Banach space E is said to be smooth if the limit

exists for all x, y ∈ U. Let C be a nonempty, closed, and convex subset of a reflexive, strictly convex and smooth Banach space E. Then, for any x ∈ E, there exists a unique point x0 ∈ C such that

The mapping P C : E → C defined by P C × = x0 is called the metric projection from E onto C. Let x ∈ E and u ∈ C. Then, it is known that u = P C × if and only if

for all y ∈ C; see [16] for more details. It is well known that if P C is a metric projection from a real Hilbert space H onto a nonempty, closed, and convex subset C, then P C is nonexpansive. However, in a general Banach space, this fact is not true.
In the sequel, we will need the following lemmas.
Lemma 2.1. [17] Let E be a uniformly convex Banach space, {α n } be a sequence of real numbers such that 0 < b ≤ α n ≤ c < 1 for all n ≥ 1, and {x n } and {y n } be sequences in E such that lim supn→∞||x n || ≤ d, lim supn→∞||y n || ≤ d and limn→∞||α n x n + (1 - α n )y n || = d. Then, limn→∞||x n - y n || = 0.
Lemma 2.2. [18] Let C be a bounded, closed, and convex subset of a uniformly convex Banach space E. Then, there exists a strictly increasing, convex, and continuous function γ : [0, ∞) → [0, ∞) such thatγ (0) = 0 and

for all 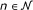 , {x1, x2,..., x
n
} ⊂ C, {λ1, λ2,..., λ
n
} ⊂ [0, 1] with
, {x1, x2,..., x
n
} ⊂ C, {λ1, λ2,..., λ
n
} ⊂ [0, 1] with  and nonexpansive mapping T of C into E.
and nonexpansive mapping T of C into E.
Following Bruck's [19] idea, we know the following result for a convex combination of nonexpansive mappings which is considered by Aoyama et al. [20] and Kimura and Nakajo [15].
Lemma 2.3. [15] Let C be a nonempty, closed, and convex subset of a uniformly convex Banach space E and {S
n
} be a family of nonexpansive mappings of C into itself such that  . Let
. Let  be a family of nonnegative numbers with indices n,
be a family of nonnegative numbers with indices n, 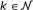 with k ≤ n such that
with k ≤ n such that
-
(i)
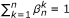 for every
for every
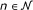 ;
;
-
(ii)
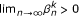 for every
for every
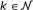
and let  for all
for all 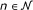 , where {α
n
} ⊂ [a, b] for some a, b ∈ (0, 1) with a ≤ b. Then, {T
n
} is a family of nonexpansive mappings of C into itself with
, where {α
n
} ⊂ [a, b] for some a, b ∈ (0, 1) with a ≤ b. Then, {T
n
} is a family of nonexpansive mappings of C into itself with  and satisfies the NST-condition.
and satisfies the NST-condition.
Now, let us turn to following well-known concept and result.
Definition 2.4. Let B be a subset of topological vector space X. A mapping G : B → 2X is called a KKM mapping if  for x
i
∈ B and i = 1, 2,..., m, where coA denotes the convex hull of the set A.
for x
i
∈ B and i = 1, 2,..., m, where coA denotes the convex hull of the set A.
Lemma 2.5. [21] Let B be a nonempty subset of a Hausdorff topological vector space × and let G : B → 2X be a KKM mapping. If G(x) is closed for all × ∈ B and is compact for at least one x ∈ B, then ⋂x∈BG(x) ≠ ∅.
3. Existence results of gep
Motivated by Takahashi and Zembayashi [22], and Ceng and Yao [23], we next prove the following crucial lemma concerning the GEP in a strictly convex, reflexive, and smooth Banach space.
Theorem 3.1. Let C be a nonempty, bounded, closed, and convex subset of a smooth, strictly convex, and reflexive Banach space E, let f be a bifunction from C × C to  satisfying (A1)-(A4), where
satisfying (A1)-(A4), where
(A1) f(x, x) = 0 for all x ∈ C;
(A2) f is monotone, i.e. f(x, y) + f(y, x) ≤ 0 for all x, y ∈ C;
(A3) for all y ∈ C, f(., y) is weakly upper semicontinuous;
(A4) for all x ∈ C, f(x,.) is convex.
Let A be α-inverse strongly monotone of C into E*. For all r > 0 and × ∈ E, define the mapping S r : E → 2C as follows:

Then, the following statements hold:
-
(1)
for each x ∈ E, S r (x) ≠ ∅;
-
(2)
S r is single-valued;
-
(3)
〈S r (x) - S r (y), J(S r x - x)〉 ≤ 〈S r (x) - S r (y), J(S r y - y)〉 for all x, y ∈ E;
-
(4)
F (S r ) = GEP (f);
-
(5)
GEP(f) is nonempty, closed, and convex.
Proof. (1) Let x0 be any given point in E. For each y ∈ C, we define the mapping G : C → 2E by

It is easily seen that y ∈ G(y), and hence G(y). ≠ ∅
-
(a)
First, we will show that G is a KKM mapping. Suppose that there exists a finite subset {y1, y2,..., y m } of C and α i > 0 with
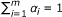 such that
such that 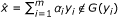 for all i = 1, 2,..., m. It follows that
for all i = 1, 2,..., m. It follows that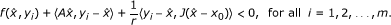
By (A1) and (A4), we have
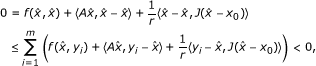
which is a contradiction. Thus, G is a KKM mapping on C.
-
(b)
Next, we show that G(y) is closed for all y ∈ C. Let {z n } be a sequence in G(y) such that z n → z as n → ∞. It then follows from z n ∈ G(y) that,
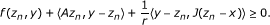 (3.2)
(3.2)By (A3), the continuity of J, and the lower semicontinuity of || · ||2, we obtain from (3.2) that
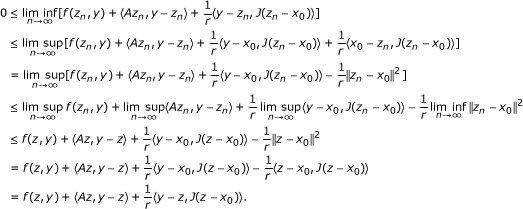
This shows that z ∈ G(y), and hence G(y) is closed for all y ∈ C.
-
(c)
We prove that G(y) is weakly compact. We now equip E with the weak topology. Then, C, as closed, bounded convex subset in a reflexive space, is weakly compact. Hence, G(y) is also weakly compact.
Using (a), (b), and (c) and Lemma 2.5, we have ⋂x∈CG(y) ≠ ∅. It is easily seen that

Hence, s r (x0) ≠ ∅. Since x0 is arbitrary, we can conclude that s r (x) ≠ ∅ for all x ∈ E.
(2) We prove that S r is single-valued. In fact, for x ∈ C and r > 0, let z1, z2 ∈ S r (x). Then,

and

Adding the two inequalities and from the condition (A2) and monotonicity of A, we have

and hence,

Hence,

Since J is monotone and E is strictly convex, we obtain that z1 - x = z2 - x and hence z1 = z2.
Therefore S r is single-valued.
(3) For x, y ∈ C, we have

and

Again, adding the two inequalities, we also have

It follows from monotonicity of A that

(4) It is easy to see that

Hence, F (S r ) = GEP (f).
(5) Finally, we claim that GEP (f) is nonempty, closed, and convex. For each y ∈ C, we define the mapping Θ : C → 2E by

Since y ∈ Θ (y), we have Θ(y) ≠ ∅ We prove that Θ is a KKM mapping on C. Suppose that there exists a finite subset {z1, z2,..., z
m
} of C and α
i
> 0 with 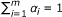 such that
such that  for all i = 1, 2,..., m. Then,
for all i = 1, 2,..., m. Then,

From (A1) and (A4), we have

which is a contradiction. Thus, Θ is a KKM mapping on C.
Next, we prove that Θ (y) is closed for each y ∈ C. For any y ∈ C, let {x n } be any sequence in Θ (y) such that x n → x0. We claim that x0 ∈ Θ (y). Then, for each y ∈ C, we have

By (A3), we see that

This shows that x0 ∈ Θ (y) and Θ(y) is closed for each y ∈ C. Thus,  is also closed.
is also closed.
We observe that Θ (y) is weakly compact. In fact, since C is bounded, closed, and convex, we also have Θ(y) is weakly compact in the weak topology. By Lemma 2.5, we can conclude that  .
.
Finally, we prove that GEP (f) is convex. In fact, let u, v ∈ F (S r ) and z t = tu+(1 - t)v for t ∈ (0, 1). From (3), we know that

This yields that

Similarly, we also have

It follows from (3.4) and (3.5) that

Hence, z t ∈ F (S r ) = GEP (f) and hence GEP (f) is convex. This completes the proof.
4. Strong convergence theorem
In this section, we prove a strong convergence theorem using a hybrid projection algorithm in a uniformly convex and smooth Banach space.
Theorem 4.1. Let E be a uniformly convex and smooth Banach space and C be a nonempty, bounded, closed, and convex subset of E. Let f be a bifunction from C × C to  satisfying (A1)-(A4), A an α-inverse strongly monotone mapping of C into E* and
satisfying (A1)-(A4), A an α-inverse strongly monotone mapping of C into E* and  a sequence of nonexpansive mappings of C into itself such that
a sequence of nonexpansive mappings of C into itself such that  and suppose that
and suppose that  satisfies the NST-condition. Let {x
n
} be the sequence in C generated by
satisfies the NST-condition. Let {x
n
} be the sequence in C generated by

where {t n } and {r n } are sequences which satisfy the following conditions:
(C1) {t n } ⊂ (0, 1) and limn→∞t n = 0;
(C2) {r n } ⊂ (0, 1) and lim infn→∞r n > 0.
Then, the sequence {x n } converges strongly to P F x0.
Proof. First, we rewrite the algorithm (4.1) as the following:

where S r is the mapping defined by (3.1) for all r > 0. We first show that the sequence {x n } is well defined. It is easy to verify that C n ∩ D n is closed and convex and Ω ⊂ C n for all n ≥ 0. Next, we prove that Ω ⊂ C n ∩ D n . Since D0 = C, we also have Ω ⊂ C0 ∩ D0. Suppose that Ω ⊂ Ck - 1∩ D k - 1 for k ≥ 2. It follows from Lemma (3) that

for all u ∈ Ω. This implies that

for all u ∈ Ω. Hence, Ω ⊂ D
k
. By the mathematical induction, we get that Ω ⊂ C
n
∩ D
n
for each n ≥ 0 and hence {x
n
} is well defined. Let w = P
F
x0. Since Ω ⊂ C
n
∩ D
n
and  , we have
, we have

Since {x
n
} is bounded, there exists a subsequence  of {x
n
} such that
of {x
n
} such that  . Since xn+2∈ Dn+1⊂ D
n
and
. Since xn+2∈ Dn+1⊂ D
n
and  , we have
, we have

Since {x
n
- x0} is bounded, we have limn→∞||x
n
- x0|| = d for some a constant d. Moreover, by the convexity of D
n
, we also have  and hence
and hence

This implies that

By Lemma 2.1, we have limn →∞||x n - xn+1|| = 0.
Next, we show that  . Since xn+1∈ C
n
and t
n
> 0, there exists
. Since xn+1∈ C
n
and t
n
> 0, there exists  , {λ0, λ1,..., λ
m
} ⊂ [0, 1] and {y0, y1,..., y
m
} ⊂ C such that
, {λ0, λ1,..., λ
m
} ⊂ [0, 1] and {y0, y1,..., y
m
} ⊂ C such that

for each i = 0, 1,..., m. Since C is bounded, by Lemma 2.2, we have

where M = supn≥0||x
n
- w||. It follows from (C1) that limn →∞||x
n
- T
n
x
n
|| = 0. Since {T
n
} satisfies the NST-condition, we have  .
.
Next, we show that v ∈ GEP (f). By the construction of D
n
, we see from (2.2) that  . Since xn+1∈ D
n
, we obtain
. Since xn+1∈ D
n
, we obtain

as n → ∞. From (C2), we also have

as n → ∞. Since {x
n
} is bounded, it has a subsequence  which weakly converges to some v ∈ E.
which weakly converges to some v ∈ E.
By (4.4), we also have  . By the definition of
. By the definition of  , for each y ∈ C, we obtain
, for each y ∈ C, we obtain

By (A3) and (4.4), we have

This shows that v ∈ GEP (f) and hence  .
.
Note that w = PΩx0. Finally, we show that x n → w as n → ∞. By the weakly lower semicontinuity of the norm, it follows from (4.3) that

This shows that

and v = w. Since E is uniformly convex, we obtain that  . It follows that
. It follows that  . Hence, we have x
n
→ w as n → w. This completes the proof.
. Hence, we have x
n
→ w as n → w. This completes the proof.
5. Deduced theorems
If we take f ≡ 0 and A ≡ 0 in Theorem 4.1, then we obtain the following result.
Theorem 5.1. Let E be a uniformly convex and smooth Banach space, C a nonempty, bounded, closed, and convex subset of E and  a sequence of nonexpansive mappings of C into itself such that
a sequence of nonexpansive mappings of C into itself such that  and suppose that
and suppose that  satisfies the NST-condition. Let {x
n
} be the sequence in C generated by
satisfies the NST-condition. Let {x
n
} be the sequence in C generated by

If {t n } ⊂ (0, 1) and limn→∞t n = 0, then {x n } converges strongly to PΩx0.
Remark 5.2. By Lemma 2.3, if we define  for all n ≥ 0 in Theorems 3.1 and 5.1, then the theorems also hold.
for all n ≥ 0 in Theorems 3.1 and 5.1, then the theorems also hold.
If we take T n ≡ I, the identity mapping on C, for all n ≥ 0 in Theorem 4.1, then we obtain the following result.
Theorem 5.3. Let E be a uniformly convex and smooth Banach space, C a nonempty, bounded, closed, and convex subset of E. Let f be a bifunction from C × C to  satisfying (A1)-(A4) and A an α-inverse strongly monotone mapping of C into E*. Let {x
n
} be the sequence in C generated by
satisfying (A1)-(A4) and A an α-inverse strongly monotone mapping of C into E*. Let {x
n
} be the sequence in C generated by

If {r n } ⊂ (0, 1) and lim infn→∞r n > 0, then {x n } converges strongly to P GEP (f) x0.
If we take A ≡ 0 in Theorem 4.1, then we obtain the following result concerning an equilibrium problem in a Banach space setting.
Theorem 5.4. Let E be a uniformly convex and smooth Banach space and C be a nonempty, bounded, closed, and convex subset of E. Let f be a bifunction from C × C to  satisfying (A1)-(A4) and let
satisfying (A1)-(A4) and let  be a sequence of nonexpansive mappings of C into itself such that
be a sequence of nonexpansive mappings of C into itself such that  and suppose that
and suppose that  satisfies the NST-condition. Let {x
n
} be the sequence in C generated by
satisfies the NST-condition. Let {x
n
} be the sequence in C generated by

where {t n } and {r n } are sequences which satisfy the conditions:
(C1) {t n } ⊂ (0, 1) and limn→∞t n = 0;
(C2) {r n } ⊂ (0, 1) and lim infn→∞r n > 0.
Then, the sequence {x n } converges strongly to PΩx0.
Abbreviations
- GEP:
-
generalized equilibrium problem.
References
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mappings in a Hilbert space. J Nonlinear Anal 2008, 69: 1025–1033. 10.1016/j.na.2008.02.042
Kohsaka F, Takahashi W: Strong convergence of an iterative sequence for maximal monotone operators in a Banach space. Abstr Appl Anal 2004, 3: 239–249.
Martinet B: Regularisation d'inequations variationnelles par approximations successives. Rev Fr Autom Inf Res Oper 1970, 4: 154–159.
Mann WR: Mean value methods in iteration. Proc Am Math Soc 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Bauschke HH, Matouskova E, Reich S: Projection and proximal point methods: convergence results and counterex-amples. Nonlinear Anal 2004, 56: 715–738. 10.1016/j.na.2003.10.010
Genal A, Lindenstrass J: An example concerning fixed points. Isr J Math 1975, 22: 81–86. 10.1007/BF02757276
Reich S: Weak convergence theorems for nonexpansive mappings in Banach spaces. J Math Anal Appl 1979, 67: 274–276. 10.1016/0022-247X(79)90024-6
Bauschke HH, Combettes PL: A weak-to-strong convergence principle for Fejer-Monotone methods in Hilbert spaces. Math Oper Res 2001, 26: 248–264. 10.1287/moor.26.2.248.10558
Shimoji K, Takahashi W: Strong convergence to common fixed points of families of nonexpansive mappings in Banach spaces. J Nonlinear Convex Anal 2007, 8: 11–34.
Nakajo K, Shimoji K, Takahashi W: Strong convergence theorems by the hybrid method for families of nonexpansive mappings in Hilbert spaces. Taiwan J Math 2006, 10: 339–360.
Takahashi W, Takeuchi Y, Kubota R: Strong convergence theorems by hybrid methods for families of nonexpansive mappings in Hilbert spaces. J Math Anal Appl 2008, 341: 276–286. 10.1016/j.jmaa.2007.09.062
Nakajo K, Takahashi W: Strong convergence theorems for nonexpansive mappings and nonexpansive semigroups. J Math Anal Appl 2003, 279: 372–379. 10.1016/S0022-247X(02)00458-4
Xu H-K: Strong convergence of approximating fixed point sequences for nonexpansive mappings. Bull Aust Math Soc 2006, 74: 143–151. 10.1017/S0004972700047535
Matsushita S, Takahashi W: Approximating fixed points of nonexpansive mappings in a Banach space by metric projections. Appl Math Comput 2008, 196: 422–425. 10.1016/j.amc.2007.06.006
Kimura Y, Nakajo K: Some characterizations for a family of nonexpansive mappings and convergence of a generated sequence to their common fixed point. Fixed Point Theory Appl 2010.
Takahashi W: Nonlinear Functional Analysis. Yokohama Publishers; 2000.
Zeidler E: Nonlinear Functional Analysis and Its Applications, vol. I: Fixed-Point Theorems. Springer, New York; 1986.
Bruck RE: On the convex approximation property and the asymptotic behaviour of nonlinear contractions in Banach spaces. Isr J Math 1981, 38: 304–314. 10.1007/BF02762776
Bruck RE: Properties of fixed-point sets of nonexpansive mappings in Banach spaces. Trans Am Math Soc 1973, 179: 251–262.
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Anal 2007, 67: 2350–2360. 10.1016/j.na.2006.08.032
Fan K: A generalization of Tychonoffs fixed point theorem. Math Ann 1961, 142: 305–310. 10.1007/BF01353421
Takahashi W, Zembayashi K: Strong and weak convergence theorems for equilibrium problems and relatively non-expansive mappings in Banach spaces. J Nonlinear Anal 2009, 70: 45–57. 10.1016/j.na.2007.11.031
Ceng L-C, Yao J-C: A hybrid iterative scheme for mixed equilibrium problems and fixed point problems. J Comput Appl Math 2008, 214: 186–201. 10.1016/j.cam.2007.02.022
Acknowledgements
U. Kamraksa was supported by grant from under the program "Strategic Scholarships for Frontier Research Network for the Ph.D." Program Thai Doctoral degree from the Office of the Higher Education Commission, Thailand. The project was supported by the "Centre of Excellence in Mathematics" under the Commission on Higher Education, Ministry of Education, Thailand and the grant from under the program Strategic Scholarships for Frontier Research Network for the Ph.D. Program Thai Doctoral degree from the Office of the Higher Education Commission.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kamraksa, U., Wangkeeree, R. Existence and iterative approximation for generalized equilibrium problems for a countable family of nonexpansive mappings in banach spaces. Fixed Point Theory Appl 2011, 11 (2011). https://doi.org/10.1186/1687-1812-2011-11
Received:
Accepted:
Published:
DOI: https://doi.org/10.1186/1687-1812-2011-11
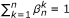 for every
for every
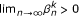 for every
for every
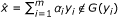 for all i = 1, 2,..., m. It follows that
for all i = 1, 2,..., m. It follows that