- Research Article
- Open access
- Published:
Nonexpansive mappings defined on unbounded domains
Fixed Point Theory and Applications volume 2006, Article number: 82080 (2006)
Abstract
We obtain fixed point theorems for nonexpansive mappings defined on unbounded sets. Our assumptions are weaker than the asymptotically contractive condition recently introduced by Jean-Paul Penot.
References
Aleyner A, Reich S: A note on explicit iterative constructions of sunny nonexpansive retractions in Banach spaces. Journal of Nonlinear and Convex Analysis 2005,6(3):525–533.
Aleyner A, Reich S: An explicit construction of sunny nonexpansive retractions in Banach spaces. Fixed Point Theory and Applications 2005,2005(3):295–305. 10.1155/FPTA.2005.295
Browder FE: Nonexpansive nonlinear operators in a Banach space. Proceedings of the National Academy of Sciences of the United States of America 1965, 54: 1041–1044. 10.1073/pnas.54.4.1041
Browder FE: Semicontractive and semiaccretive nonlinear mappings in Banach spaces. Bulletin of the American Mathematical Society 1968, 74: 660–665. 10.1090/S0002-9904-1968-11983-4
Bruck RE Jr.: Properties of fixed-point sets of nonexpansive mappings in Banach spaces. Transactions of the American Mathematical Society 1973, 179: 251–262.
Bruck RE Jr.: A common fixed point theorem for a commuting family of nonexpansive mappings. Pacific Journal of Mathematics 1974, 53: 59–71.
Bula I: Some generalizations of W. A. Kirk's fixed point theorems. In Mathematics, Latv. Univ. Zināt. Raksti. Volume 595. Latv. Univ., Riga; 1994:159–166.
Caristi J: Fixed point theorems for mappings satisfying inwardness conditions. Transactions of the American Mathematical Society 1976, 215: 241–251.
García-Falset J: Fixed points for mappings with the range type condition. Houston Journal of Mathematics 2002,28(1):143–158.
Gatica JA, Kirk WA: Fixed point theorems for contraction mappings with applications to nonexpansive and pseudo-contractive mappings. The Rocky Mountain Journal of Mathematics 1974, 4: 69–79. 10.1216/RMJ-1974-4-1-69
Goebel K, Reich S: Uniform Convexity, Hyperbolic Geometry, and Nonexpansive Mappings, Monographs and Textbooks in Pure and Applied Mathematics. Volume 83. Marcel Dekker, New York; 1984:ix+170.
Göhde D: Zum Prinzip der kontraktiven Abbildung. Mathematische Nachrichten 1965, 30: 251–258. 10.1002/mana.19650300312
Kato T: Nonlinear semigroups and evolution equations. Journal of the Mathematical Society of Japan 1967, 19: 508–520. 10.2969/jmsj/01940508
Kirk WA: A fixed point theorem for mappings which do not increase distances. The American Mathematical Monthly 1965, 72: 1004–1006. 10.2307/2313345
Kirk WA: Fixed point theorems for nonexpansive mappings satisfying certain boundary conditions. Proceedings of the American Mathematical Society 1975, 50: 143–149. 10.1090/S0002-9939-1975-0380527-7
Kirk WA, Morales CH: Nonexpansive mappings: boundary/inwardness conditions and local theory. In Handbook of Metric Fixed Point Theory. Kluwer Academic, Dordrecht; 2001:299–321.
Kirk WA, Schöneberg R: Some results on pseudo-contractive mappings. Pacific Journal of Mathematics 1977,71(1):89–100.
Luc DT: Recessively compact sets: properties and uses. Set-Valued Analysis 2002,10(1):15–35. 10.1023/A:1014458603461
Luc DT, Penot J-P: Convergence of asymptotic directions. Transactions of the American Mathematical Society 2001,353(10):4095–4121. 10.1090/S0002-9947-01-02664-2
Matsushita S-Y, Takahashi W: Weak and strong convergence theorems for relatively nonexpansive mappings in Banach spaces. Fixed Point Theory and Applications 2004,2004(1):37–47. 10.1155/S1687182004310089
Penot J-P: A fixed-point theorem for asymptotically contractive mappings. Proceedings of the American Mathematical Society 2003,131(8):2371–2377. 10.1090/S0002-9939-03-06999-5
Penot J-P: A metric approach to asymptotic analysis. Bulletin des Sciences Mathématiques 2003,127(9):815–833. 10.1016/j.bulsci.2003.08.001
Petryshyn WV: Structure of the fixed points sets of
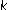 -set-contractions. Archive for Rational Mechanics and Analysis 1970/1971, 40: 312–328.
-set-contractions. Archive for Rational Mechanics and Analysis 1970/1971, 40: 312–328.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Kaewcharoen, A., Kirk, W. Nonexpansive mappings defined on unbounded domains. Fixed Point Theory Appl 2006, 82080 (2006). https://doi.org/10.1155/FPTA/2006/82080
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/FPTA/2006/82080
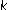 -set-contractions. Archive for Rational Mechanics and Analysis 1970/1971, 40: 312–328.
-set-contractions. Archive for Rational Mechanics and Analysis 1970/1971, 40: 312–328.