- Research Article
- Open access
- Published:
Algebraic periods of self-maps of a rational exterior space of rank 2
Fixed Point Theory and Applications volume 2006, Article number: 80521 (2006)
Abstract
The paper presents a complete description of the set of algebraic periods for self-maps of a rational exterior space which has rank 2.
References
Alsedà L, Baldwin S, Llibre J, Swanson R, Szlenk W: Minimal sets of periods for torus maps via Nielsen numbers. Pacific Journal of Mathematics 1995,169(1):1–32.
Chandrasekharan K: Introduction to Analytic Number Theory, Die Grundlehren der mathematischen Wissenschaften. Volume 148. Springer, New York; 1968.
Fagella N, Llibre J: Periodic points of holomorphic maps via Lefschetz numbers. Transactions of the American Mathematical Society 2000,352(10):4711–4730. 10.1090/S0002-9947-00-02608-8
Graff G: Existence of
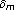 -periodic points for smooth maps of compact manifold. Hokkaido Mathematical Journal 2000,29(1):11–21.
-periodic points for smooth maps of compact manifold. Hokkaido Mathematical Journal 2000,29(1):11–21.Graff G: Minimal periods of maps of rational exterior spaces. Fundamenta Mathematicae 2000,163(2):99–115.
Guillamon A, Jarque X, Llibre J, Ortega J, Torregrosa J: Periods for transversal maps via Lefschetz numbers for periodic points. Transactions of the American Mathematical Society 1995,347(12):4779–4806. 10.2307/2155063
Haibao D: The Lefschetz numbers of iterated maps. Topology and its Applications 1995,67(1):71–79. 10.1016/0166-8641(95)98773-J
Jezierski J, Marzantowicz M: Homotopy Methods in Topological Fixed and Periodic Point Theory. Springer, Dordrech; 2005.
Jiang B, Llibre J: Minimal sets of periods for torus maps. Discrete and Continuous Dynamical Systems 1998,4(2):301–320.
Llibre J: Lefschetz numbers for periodic points. In Nielsen Theory and Dynamical Systems (South Hadley, Mass, 1992), Contemp. Math.. Volume 152. American Mathematical Society, Rhode Island; 1993:215–227.
Llibre J, Paraños J, Rodríguez JA: Periods for transversal maps on compact manifolds with a given homology. Houston Journal of Mathematics 1998,24(3):397–407.
Marzantowicz W, Przygodzki PM: Finding periodic points of a map by use of a
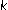 -adic expansion. Discrete and Continuous Dynamical Systems 1999,5(3):495–514.
-adic expansion. Discrete and Continuous Dynamical Systems 1999,5(3):495–514.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Graff, G. Algebraic periods of self-maps of a rational exterior space of rank 2. Fixed Point Theory Appl 2006, 80521 (2006). https://doi.org/10.1155/FPTA/2006/80521
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1155/FPTA/2006/80521
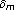 -periodic points for smooth maps of compact manifold. Hokkaido Mathematical Journal 2000,29(1):11–21.
-periodic points for smooth maps of compact manifold. Hokkaido Mathematical Journal 2000,29(1):11–21.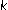 -adic expansion. Discrete and Continuous Dynamical Systems 1999,5(3):495–514.
-adic expansion. Discrete and Continuous Dynamical Systems 1999,5(3):495–514.