- Research Article
- Open access
- Published:
The Iterative Method of Generalized 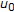 -Concave Operators
-Concave Operators
Fixed Point Theory and Applications volume 2011, Article number: 979261 (2011)
Abstract
We define the concept of the generalized  -concave operators, which generalize the definition of the
-concave operators, which generalize the definition of the  -concave operators. By using the iterative method and the partial ordering method, we prove the existence and uniqueness of fixed points of this class of the operators. As an example of the application of our results, we show the existence and uniqueness of solutions to a class of the Hammerstein integral equations.
-concave operators. By using the iterative method and the partial ordering method, we prove the existence and uniqueness of fixed points of this class of the operators. As an example of the application of our results, we show the existence and uniqueness of solutions to a class of the Hammerstein integral equations.
1. Introduction and Preliminary
In [1, 2], Collatz divided the typical problems in computation mathematics into five classes, and the first class is how to solve the operator equation

by the iterative method, that is, construct successively the sequence

for some initial  to solve (1.1).
to solve (1.1).
Let  be a cone in real Banach space
be a cone in real Banach space  and the partial ordering ≤ defined by
and the partial ordering ≤ defined by  , that is,
, that is,  if and only if
if and only if  . The concept and properties of the cone can be found in [3–5]. People studied how to solve (1.1) by using the iterative method and the partial ordering method (see [1–11]).
. The concept and properties of the cone can be found in [3–5]. People studied how to solve (1.1) by using the iterative method and the partial ordering method (see [1–11]).
In [7], Krasnosel'skiĭ gave the concept of  concave operators and studied the existence and uniqueness of the fixed point for the operator by the iterative method. The concept of
concave operators and studied the existence and uniqueness of the fixed point for the operator by the iterative method. The concept of  concave operators was defined by Krasnosel'skiĭ as follows.
concave operators was defined by Krasnosel'skiĭ as follows.
Let operator  and
and  . Suppose that
. Suppose that
(i)for any  , there exist
, there exist  and
and  , such that
, such that

(ii)for any  satisfying
satisfying 
 ,
,  ) and any
) and any  , there exists
, there exists  , such that
, such that

Then  is called an
is called an  concave operator.
concave operator.
In many papers, the authors studied  concave operators and obtained some results (see [3–5, 8–15]). In this paper, we generalize the concept of
concave operators and obtained some results (see [3–5, 8–15]). In this paper, we generalize the concept of  concave operators, give a concept of the generalized
concave operators, give a concept of the generalized  concave operators, and study the existence and uniqueness of fixed points for this class of operators by the iterative method. Our results generalize the results in [3, 4, 7, 15].
concave operators, and study the existence and uniqueness of fixed points for this class of operators by the iterative method. Our results generalize the results in [3, 4, 7, 15].
2. Main Result
In this paper, we always let  be a cone in real Banach space
be a cone in real Banach space  and the partial ordering ≤ defined by
and the partial ordering ≤ defined by  . Given
. Given  , let
, let  .
.
Definition 2.1.
Let operator  and
and  . Suppose that
. Suppose that
(i)for any  , there exist
, there exist  and
and  , such that
, such that

(ii)for any  satisfying
satisfying  (
( ,
,  ) and any
) and any  , there exists
, there exists  , such that
, such that

Then  is called a generalized
is called a generalized  concave operator.
concave operator.
Remark 2.2.
In Definition 2.1, let  , we get the definition of the
, we get the definition of the  concave operator.
concave operator.
Theorem 2.3.
Let operator  be generalized
be generalized  -concave and increasing (i.e.,
-concave and increasing (i.e.,  ), then
), then  has at most one fixed point in
has at most one fixed point in  .
.
Proof.
Let  ,
,  be two different fixed points of
be two different fixed points of  , that is,
, that is,  ,
,  , and
, and  . By Definition 2.1, there exist real numbers
. By Definition 2.1, there exist real numbers  ,
,  ,
,  ,
,  , such that
, such that

Hence  .
.
Let  ,
,  , we get that
, we get that  , that is,
, that is,  . Let
. Let

hence  , that is,
, that is,  , then
, then  .
.
Next we will show that  . Assume that
. Assume that  ; by (2.2) and (2.4), there exists
; by (2.2) and (2.4), there exists  , such that
, such that

By (2.2), there exists  , such that
, such that

hence,

Therefore,

Obviously, by (2.5) and (2.8), we get

Let  , we have
, we have

in contradiction to the definition of  . Therefore,
. Therefore,  .
.
By (2.4),  . The proof is completed.
. The proof is completed.
To prove the following Theorem 2.4, we will use the definition of the  -norm as follows.
-norm as follows.
Given  , set
, set

It is easy to see that  becomes a normed linear space under the norm
becomes a normed linear space under the norm  .
.  is called the
is called the  norm of the element
norm of the element  (see [3, 4]).
(see [3, 4]).
Theorem 2.4.
Let operator  be increasing and generalized
be increasing and generalized  concave. Suppose that
concave. Suppose that  has a fixed point
has a fixed point  in
in  , then, constructing successively the sequence
, then, constructing successively the sequence  for any initial
for any initial  , we have
, we have  .
.
Proof.
Suppose that  is generated from
is generated from  . Take
. Take  , such that
, such that  . Let
. Let  , and constructing successively the sequences
, and constructing successively the sequences  ,
,  . Since
. Since  is a generalized
is a generalized  concave operator, we know that there exists
concave operator, we know that there exists  , such that
, such that

hence,  , then
, then

By (2.2), we can easily get  . So it is easy to show that
. So it is easy to show that

Let

then,

which implies that the limit of  exists. Let
exists. Let  , then
, then  .
.
Next we will show that  . Suppose that
. Suppose that  . Since
. Since  is a generalized
is a generalized  concave operator, then there exists
concave operator, then there exists  , such that
, such that

Moreover,

Therefore,

By (2.17) and (2.19), for any  , there exists
, there exists  , such that
, such that

Particularly, for any  , we have
, we have

where  .
.
Hence,

By (2.15), and (2.22), we get  therefore,
therefore,  , in contradiction to
, in contradiction to  . Hence,
. Hence,

Since  is a generalized
is a generalized  -concave operator, thus there exist real numbers
-concave operator, thus there exist real numbers  ,
,  , such that
, such that  , and
, and  , we have
, we have

Moreover

Hence,

Consequently, by (2.23), we get  .
.
To prove the following Theorem 2.5, we will use the definition of the normal cone as follows.
Let  be a cone in
be a cone in  . Suppose that there exist constants
. Suppose that there exist constants  , such that
, such that

then  is said to be normal, and the smallest
is said to be normal, and the smallest  is called the normal constant of
is called the normal constant of  (see [3–5]).
(see [3–5]).
Theorem 2.5.
Let  be a normal cone of
be a normal cone of  . If operator
. If operator  is increasing and generalized
is increasing and generalized  -concave, and
-concave, and  is irrelevant to
is irrelevant to  in (2.2), then
in (2.2), then  has the only one fixed point
has the only one fixed point  . Moreover, constructing successively the sequence
. Moreover, constructing successively the sequence  for any initial
for any initial  , we have
, we have  .
.
Proof.
Since  is a generalized
is a generalized  concave operator, hence there exist real numbers
concave operator, hence there exist real numbers  , such that
, such that  . Take
. Take  small enough, then
small enough, then  .
.
Therefore,  , that is,
, that is,  is an increasing sequence and
is an increasing sequence and  , hence, the limit of
, hence, the limit of  exists. Set
exists. Set  , then
, then  .
.
Let  , where
, where  which is irrelevant to
which is irrelevant to  is
is  in (2.2), and
in (2.2), and  is increasing, so
is increasing, so  . By
. By  , we can choose a natural number
, we can choose a natural number  big enough, such that
big enough, such that

Let

Obviously,  . Since
. Since  is increasing, we have
is increasing, we have

Since  , we get
, we get  . Hence
. Hence

then  . It is easy to see
. It is easy to see

Let

Obviously,  . So
. So  .
.
Therefore,  , that is,
, that is,  is an increasing sequence and
is an increasing sequence and  , hence, the limit of
, hence, the limit of  exists. Set
exists. Set  , then
, then  .
.
Next we will show that  . Suppose that
. Suppose that  , we have the following.
, we have the following.
-
(i)
If for any natural number n,
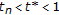 , then
, then  (2.34)
(2.34)
hence,

Taking limits, we have  , a contradiction.
, a contradiction.
-
(ii)
Suppose that there exists a natural number
 , such that
, such that 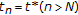 .
.
When  , so we have
, so we have

then  , a contradiction.
, a contradiction.
Therefore,  .
.
For any natural numbers  , we have
, we have

Similarly,  . By the normality of
. By the normality of  and
and  , we get
, we get

where  is the normal constant of
is the normal constant of  . Hence the limits of
. Hence the limits of  and
and  exist. Let
exist. Let  , then
, then  , hence,
, hence,

That is,  . Let
. Let  , then
, then  .
.
Taking limits, we get  . Hence
. Hence  , that is,
, that is,  is a fixed point of
is a fixed point of  . By Theorem 2.4, the conclusions of Theorem 2.5 hold. The proof is completed.
. By Theorem 2.4, the conclusions of Theorem 2.5 hold. The proof is completed.
3. Examples
Example 3.1.
Let  , let
, let is continuous}, let
is continuous}, let , let
, let  ,
,  , then
, then  is a real Banach space and
is a real Banach space and  is a normal and solid cone in
is a normal and solid cone in  (
( is called solid if it contains interior points, i.e.,
is called solid if it contains interior points, i.e.,  ). Take
). Take  , let
, let  ,
,  ,
,  , and
, and  .
.
Considering the Hammerstein integral equation

where  is continuous,
is continuous,  is increasing for
is increasing for  . Suppose that
. Suppose that
(1)there exist real numbers  , such that
, such that  ,
,  , and
, and  ,
, ,
,
(2)for any  and
and  , there exists
, there exists  , such that
, such that

Then (3.1) has the only one solution  . Moreover, constructing successively the sequence:
. Moreover, constructing successively the sequence:

for any initial  , we have
, we have  .
.
Proof.
Considering the operator

Obviously,  is increasing. Therefore, (i) of Definition 2.1 is satisfied. For any
is increasing. Therefore, (i) of Definition 2.1 is satisfied. For any  , by (3.2), we have
, by (3.2), we have

Therefore, (ii) of Definition 2.1 is satisfied. Hence the operator  is generalized
is generalized  -concave. Consequently, operator
-concave. Consequently, operator  satisfies all conditions of Theorem 2.5, thus the conclusion of Example 3.1 holds.
satisfies all conditions of Theorem 2.5, thus the conclusion of Example 3.1 holds.
Example 3.2.
Let  be a real numbers set, and let
be a real numbers set, and let  ,
,  , then
, then  is a real Banach space and
is a real Banach space and  is a normal and solid cone in
is a normal and solid cone in  . Let
. Let  . Considering the equation:
. Considering the equation:  . Obviously,
. Obviously,  is a generalized
is a generalized  -concave operator and satisfies all the conditions of Theorem 2.5. Hence
-concave operator and satisfies all the conditions of Theorem 2.5. Hence  has the only one fixed point
has the only one fixed point  . Moreover, we know
. Moreover, we know  by computing.
by computing.
In Example 3.2, we know that operator  doesn't satisfy the definition of
doesn't satisfy the definition of  -concave operators. Therefore, we can't obtain the fixed point of
-concave operators. Therefore, we can't obtain the fixed point of  by the fixed point theorem of
by the fixed point theorem of  -concave operators. The
-concave operators. The  -concave operators' fixed points are all positive, but here
-concave operators' fixed points are all positive, but here  's fixed point is negative.
's fixed point is negative.
References
Collatz L: The theoretical basis of numerical mathematics. Mathematics Asian Studies 1966, 4: 1–17.
Collatz L: Function analysis as the assistant tool for Numerical Mathematics. Mathematics Asian Studies 1966, 4: 53–60.
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Guo D: Nonlinear Functional Analysis. Science and Technology Press, Shandong, China; 1985.
Sun Jingxian: Nonlinear Functional Analysis and Applications. Science Press, Beijing, China; 2007.
Krasnosel'skii MA, et al.: Approximate Solution of Operator Equations. Wolters-Noordhoff; 1972.
Krasnosel'skiĭ MA, Zabreĭko PP: Geometrical Methods of Nonlinear Analysis, Fundamental Principles of Mathematical Sciences. Volume 263. Springer, Berlin, Germany; 1984:xix+409.
Guo D: The partial order in non-linear analysis. Shandong Science and Technology Press, Ji'nan, China; 2000.
Zhao Z: Uniqueness and existence of fixed point on some mixed monotone mappings in ordered linear spaces. Journal of Systems Science and Complexity 1999,19(4):217–224.
Sun JX, Liu LS: An iterative solution method for nonlinear operator equations and its applications. Acta Mathematica Scientia. Series A 1993,13(2):141–145.
Sun JX: Some new fixed point theorems of increasing operators and applications. Applicable Analysis 1991,42(3–4):263–273.
Wang WX, Liang ZD: Fixed point theorems for a class of nonlinear operators and their applications. Acta Mathematica Sinica. Chinese Series 2005,48(4):789–800.
Liang ZD, Wang WX, Li SJ: On concave operators. Acta Mathematica Sinica (English Series) 2006,22(2):577–582. 10.1007/s10114-005-0687-1
Krasnosel'skii MA: Positive Solution of Operators Equations. Noordoff, Groningen, The Netherlands; 1964.
Zhai CB, Li YJ: Fixed point theorems for u 0 -concave operators and their applications. Acta Mathematica Scientia. Series A 2008,28(6):1023–1028.
Acknowledgment
The project is supported by the National Science Foundation of China (10971179), the College Graduate Research and Innovation Plan Project of Jiangsu (CX10S−037Z), the Graduate Research and Innovation Programs of Xuzhou Normal University Innovation Plan (2010YLA001).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Zhou, Y., Sun, J. & Sun, J. The Iterative Method of Generalized 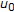 -Concave Operators.
Fixed Point Theory Appl 2011, 979261 (2011). https://doi.org/10.1155/2011/979261
-Concave Operators.
Fixed Point Theory Appl 2011, 979261 (2011). https://doi.org/10.1155/2011/979261
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/979261
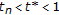 , then
, then 
 , such that
, such that 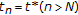 .
.