- Research Article
- Open access
- Published:
Convergence Analysis for a System of Generalized Equilibrium Problems and a Countable Family of Strict Pseudocontractions
Fixed Point Theory and Applications volume 2011, Article number: 941090 (2011)
Abstract
We introduce a new iterative algorithm for a system of generalized equilibrium problems and a countable family of strict pseudocontractions in Hilbert spaces. We then prove that the sequence generated by the proposed algorithm converges strongly to a common element in the solutions set of a system of generalized equilibrium problems and the common fixed points set of an infinitely countable family of strict pseudocontractions.
1. Introduction
Let  be a real Hilbert space with the inner product
be a real Hilbert space with the inner product  and inducted norm
and inducted norm  . Let
. Let  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  . Let
. Let  be a family of bifunctions, and let
be a family of bifunctions, and let  be a family of nonlinear mappings, where
be a family of nonlinear mappings, where  is an arbitrary index set. The system of generalized equilibrium problems is to find
is an arbitrary index set. The system of generalized equilibrium problems is to find  such that
such that

If  is a singleton, then (1.1) reduces to find
is a singleton, then (1.1) reduces to find  such that
such that

The solutions set of (1.2) is denoted by  . If
. If  , then the solutions set of (1.2) is denoted by
, then the solutions set of (1.2) is denoted by  , and if
, and if  , then the solutions set of (1.2) is denoted by
, then the solutions set of (1.2) is denoted by  . The problem (1.2) is very general in the sense that it includes, as special cases, optimization problems, variational inequalities, minimax problems, and the Nash equilibrium problem in noncooperative games; see also [1, 2]. Some methods have been constructed to solve the system of equilibrium problems (see, e.g., [3–7]). Recall that a mapping
. The problem (1.2) is very general in the sense that it includes, as special cases, optimization problems, variational inequalities, minimax problems, and the Nash equilibrium problem in noncooperative games; see also [1, 2]. Some methods have been constructed to solve the system of equilibrium problems (see, e.g., [3–7]). Recall that a mapping  is said to be
is said to be
(1)monotone if

(2)α-inverse-strongly monotone if there exists a constant  such that
such that

It is easy to see that if  is α-inverse-strongly monotone, then
is α-inverse-strongly monotone, then  is monotone and
is monotone and  -Lipschitz.
-Lipschitz.
For solving the equilibrium problem, let us assume that  satisfies the following conditions:
satisfies the following conditions:
(A1) for all
for all  ,
,
(A2) is monotone, that is,
is monotone, that is,  for all
for all  ,
,
(A3)for each  ,
,  ,
,
(A4)for each  ,
,  is convex and lower semicontinuous.
is convex and lower semicontinuous.
Throughout this paper, we denote the fixed points set of a nonlinear mapping  by
by  . Recall that
. Recall that  is said to be a
is said to be a  -strict pseudocontraction if there exists a constant
-strict pseudocontraction if there exists a constant  such that
such that

It is well known that (1.5) is equivalent to

It is worth mentioning that the class of strict pseudocontractions includes properly the class of nonexpansive mappings. It is also known that every  -strict pseudocontraction is
-strict pseudocontraction is  -Lipschitz; see [8].
-Lipschitz; see [8].
In 1953, Mann [9] introduced the iteration as follows: a sequence  defined by
defined by and
and

where  . If
. If  is a nonexpansive mapping with a fixed point and the control sequence
is a nonexpansive mapping with a fixed point and the control sequence  is chosen so that
is chosen so that  , then the sequence
, then the sequence  defined by (1.7) converges weakly to a fixed point of
defined by (1.7) converges weakly to a fixed point of  (this is also valid in a uniformly convex Banach space with the Fréchet differentiable norm [10]).
(this is also valid in a uniformly convex Banach space with the Fréchet differentiable norm [10]).
In 1967, Browder and Petryshyn [11] introduced the class of strict pseudocontractions and proved existence and weak convergence theorems in a real Hilbert setting by using Mann iterative algorithm (1.7) with a constant sequence  for all
for all  . Recently, Marino and Xu [8] and Zhou [12] extended the results of Browder and Petryshyn [11] to Mann's iteration process (1.7). Since 1967, the construction of fixed points for pseudocontractions via the iterative process has been extensively investigated by many authors (see, e.g., [13–22]).
. Recently, Marino and Xu [8] and Zhou [12] extended the results of Browder and Petryshyn [11] to Mann's iteration process (1.7). Since 1967, the construction of fixed points for pseudocontractions via the iterative process has been extensively investigated by many authors (see, e.g., [13–22]).
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Let
. Let  be a nonexpansive mapping,
be a nonexpansive mapping,  a bifunction, and let
a bifunction, and let  be an inverse-strongly monotone mapping.
be an inverse-strongly monotone mapping.
In 2008, Moudafi [23] introduced an iterative method for approximating a common element of the fixed points set of a nonexpansive mapping  and the solutions set of a generalized equilibrium problem
and the solutions set of a generalized equilibrium problem  as follows: a sequence
as follows: a sequence  defined by
defined by  and
and

where  and
and  . He proved that the sequence
. He proved that the sequence  generated by (1.8) converges weakly to an element in
generated by (1.8) converges weakly to an element in  under suitable conditions.
under suitable conditions.
Due to the weak convergence, recently, S. Takahashi and W. Takahashi [24] introduced another modification iterative method of (1.8) for finding a common element of the fixed points set of a nonexpansive mapping and the solutions set of a generalized equilibrium problem in the framework of a real Hilbert space. To be more precise, they proved the following theorem.
Theorem 1.1 (see [24]).
Let  be a closed convex subset of a real Hilbert space
be a closed convex subset of a real Hilbert space  , and let
, and let  be a bifunction satisfying (A1)–(A4). Let
be a bifunction satisfying (A1)–(A4). Let  be an α-inverse-strongly monotone mapping of
be an α-inverse-strongly monotone mapping of  into
into  , and let
, and let  be a nonexpansive mapping of
be a nonexpansive mapping of  into itself such that
into itself such that  . Let
. Let  and
and  , and let
, and let  and
and  be sequences generated by
be sequences generated by

where  ,
,  and
and  satisfy
satisfy
(i) and
and  ,
,
(ii) ,
,
(iii) ,
,
(iv) .
.
Then,  converges strongly to
converges strongly to  .
.
Recently, Yao et al. [25] introduced a new modified Mann iterative algorithm which is different from those in the literature for a nonexpansive mapping in a real Hilbert space. To be more precise, they proved the following theorem.
Theorem 1.2 (see [25]).
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Let
. Let  be a nonexpansive mapping such that
be a nonexpansive mapping such that  . Let
. Let  , and let
, and let  be two real sequences in
be two real sequences in  . For given
. For given  arbitrarily, let the sequence
arbitrarily, let the sequence  ,
,  , be generated iteratively by
, be generated iteratively by

Suppose that the following conditions are satisfied:
(i) and
and  ,
,
(ii) ,
,
then, the sequence  generated by (1.10) strongly converges to a fixed point of
generated by (1.10) strongly converges to a fixed point of  .
.
We know the following crucial lemmas concerning the equilibrium problem in Hilbert spaces.
Lemma 1.3 (see [1]).
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  , let
, let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4). Let
satisfying (A1)–(A4). Let  and
and  . Then, there exists
. Then, there exists  such that
such that

Lemma 1.4 (see [26]).
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Let
. Let  be a bifunction from
be a bifunction from  to
to  satisfying (A1)–(A4). For
satisfying (A1)–(A4). For  and
and  , define the mapping
, define the mapping  as follows:
as follows:

Then, the following statements hold:
(1) is single-valued,
is single-valued,
(2) is firmly nonexpansive, that is, for any
is firmly nonexpansive, that is, for any  ,
,

(3) ,
,
(4) is closed and convex.
is closed and convex.
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Let
. Let  for each
for each  . Let
. Let  be a family of bifunctions, let
be a family of bifunctions, let  be a family of
be a family of  -inverse-strongly monotone mappings, and let
-inverse-strongly monotone mappings, and let  be a countable family of
be a countable family of  -strict pseudocontractions. For each
-strict pseudocontractions. For each  , denote the mapping
, denote the mapping  by
by  , where
, where  is the mapping defined as in Lemma 1.4.
is the mapping defined as in Lemma 1.4.
Motivated and inspired by Marino and Xu [8], Moudafi [23], S. Takahashi and W. Takahashi [24], and Yao et al. [25], we consider the following iteration:  and
and

where  ,
,  and
and  .
.
In this paper, we first prove a path convergence result for a nonexpansive mapping and a system of generalized equilibrium problems. Then, we prove a strong convergence theorem of the iteration process (1.14) for a system of generalized equilibrium problems and a countable family of strict pseudocontractions in a real Hilbert space. Our results extend the main results obtained by Yao et al. [25] in several aspects.
2. Preliminaries
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . For each
. For each  , there exists a unique nearest point in
, there exists a unique nearest point in  , denoted by
, denoted by  , such that
, such that  .
.  is called the metric projection of
is called the metric projection of  onto
onto  . It is also known that for
. It is also known that for  and
and  ,
,  is equivalent to
is equivalent to  for all
for all  . Furthermore,
. Furthermore,

for all  ,
,  . In a real Hilbert space, we also know that
. In a real Hilbert space, we also know that

for all  and
and  .
.
In the sequel, we need the following lemmas.
Let  be a real uniformly convex Banach space, and let
be a real uniformly convex Banach space, and let  be a nonempty, closed, and convex subset of
be a nonempty, closed, and convex subset of  , and let
, and let  be a nonexpansive mapping such that
be a nonexpansive mapping such that  , then
, then  is demiclosed at zero.
is demiclosed at zero.
Lemma 2.2 (see [29]).
Let  and
and  be two sequences in a Banach space
be two sequences in a Banach space  such that
such that

where  satisfies conditions:
satisfies conditions:  . If
. If  , then
, then  as
as  .
.
Lemma 2.3 (see [30]).
Assume that  is a sequence of nonnegative real numbers such that
is a sequence of nonnegative real numbers such that

where  is a sequence in
is a sequence in  and
and  is a sequence in
is a sequence in  such that
such that
(a)  ; (b)
; (b)  or
or  .Then,
.Then,  .
.
Lemma 2.4 (see [31]).
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Let the mapping
. Let the mapping  be α-inverse-strongly monotone, and let
be α-inverse-strongly monotone, and let  be a constant. Then, we have
be a constant. Then, we have

for all  . In particular, if
. In particular, if  , then
, then  is nonexpansive.
is nonexpansive.
To deal with a family of mappings, the following conditions are introduced: let  be a subset of a real Hilbert space
be a subset of a real Hilbert space  , and let
, and let  be a family of mappings of
be a family of mappings of  such that
such that  . Then,
. Then,  is said to satisfy the
is said to satisfy the  -condition [32] if for each bounded subset
-condition [32] if for each bounded subset  of
of  ,
,

Lemma 2.5 (see [32]).
Let  be a nonempty and closed subset of a Hilbert space
be a nonempty and closed subset of a Hilbert space  , and let
, and let  be a family of mappings of
be a family of mappings of  into itself which satisfies the
into itself which satisfies the  -condition. Then, for each
-condition. Then, for each  ,
,  converges strongly to a point in
converges strongly to a point in  . Moreover, let the mapping
. Moreover, let the mapping  be defined by
be defined by

Then, for each bounded subset  of
of  ,
,

The following results can be found in [33, 34].
Let  be a closed, and convex subset of a Hilbert space
be a closed, and convex subset of a Hilbert space  . Suppose that
. Suppose that  is a family of
is a family of  -strictly pseudocontractive mappings from
-strictly pseudocontractive mappings from  into
into  with
with  and
and  is a real sequence in
is a real sequence in  such that
such that  . Then, the following conclusions hold:
. Then, the following conclusions hold:
(1) is a
is a  -strictly pseudocontractive mapping,
-strictly pseudocontractive mapping,
(2) .
.
Lemma 2.7 (see [34]).
Let  be a closed and convex subset of a Hilbert space
be a closed and convex subset of a Hilbert space  . Suppose that
. Suppose that  is a countable family of
is a countable family of  -strictly pseudocontractive mappings of
-strictly pseudocontractive mappings of  into itself with
into itself with  . For each
. For each  , define
, define  by
by

where  is a family of nonnegative numbers satisfying
is a family of nonnegative numbers satisfying
(i) for all
for all  ,
,
(ii) for all
for all  ,
,
(iii) .
.
Then,
(1)Each  is a
is a  -strictly pseudocontractive mapping.
-strictly pseudocontractive mapping.
(2) satisfies
satisfies  -condition.
-condition.
(3)If  is defined by
is defined by

then  and
and  .
.
In the sequel, we will write  satisfies the
satisfies the  -condition if
-condition if  satisfies the
satisfies the  -condition and
-condition and  is defined by Lemma 2.5 with
is defined by Lemma 2.5 with  .
.
3. Path Convergence Results
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Let
. Let  be a nonexpansive mapping. Let
be a nonexpansive mapping. Let  be a family of bifunctions, let
be a family of bifunctions, let  be a family of
be a family of  -inverse-strongly monotone mappings, and let
-inverse-strongly monotone mappings, and let  . For each
. For each  , we denote the mapping
, we denote the mapping  by
by

where  is the mapping defined as in Lemma 1.4. For each
is the mapping defined as in Lemma 1.4. For each  , we define the mapping
, we define the mapping  as follows:
as follows:

By Lemmas 1.4(2) and 2.4, we know that  and
and  are nonexpansive for each
are nonexpansive for each  . So, the mapping
. So, the mapping  is also nonexpansive for each
is also nonexpansive for each  . Moreover, we can check easily that
. Moreover, we can check easily that  is a contraction. Then, the Banach contraction principle ensures that there exists a unique fixed point
is a contraction. Then, the Banach contraction principle ensures that there exists a unique fixed point  of
of  in
in  , that is,
, that is,

Theorem 3.1.
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Let
. Let  be a nonexpansive mapping. Let
be a nonexpansive mapping. Let  be a family of bifunctions, let
be a family of bifunctions, let  be a family of
be a family of  -inverse-strongly monotone mappings, and let
-inverse-strongly monotone mappings, and let  . For each
. For each  , let the mapping
, let the mapping  be defined by (3.1). Assume that
be defined by (3.1). Assume that  . For each
. For each  , let the net
, let the net  be generated by (3.3). Then, as
be generated by (3.3). Then, as  , the net
, the net  converges strongly to an element in
converges strongly to an element in  .
.
Proof.
First, we show that  is bounded. For each
is bounded. For each  , let
, let  and
and  . From (3.3), we have for each
. From (3.3), we have for each  that
that

It follows that

Hence,  is bounded and so are
is bounded and so are  and
and  . Observe that
. Observe that

as  since
since  is bounded.
is bounded.
Next, we show that  as
as  . Denote
. Denote  for any
for any  and
and  . We note that
. We note that  for each
for each  . From Lemma 2.4, we have for each
. From Lemma 2.4, we have for each  and
and  that
that

It follows that

where  . So, we have
. So, we have

which implies that

for each  . Since
. Since  is firmly nonexpansive for each
is firmly nonexpansive for each  , we have for each
, we have for each  and
and  that
that

This implies that

where  . This shows that
. This shows that

Hence,

From (3.10), we obtain

as  . So, we can conclude that
. So, we can conclude that

for each  . Observing
. Observing

it follows by (3.16) that

From (3.6) and (3.18), we have

Hence,

as  .
.
Next, we show that  is relatively norm compact as
is relatively norm compact as  . Let
. Let  be a sequence such that
be a sequence such that  as
as  . Put
. Put  . From (3.20), we obtain
. From (3.20), we obtain

Since  is bounded, without loss of generality, we may assume that
is bounded, without loss of generality, we may assume that  converges weakly to
converges weakly to  . Applying Lemma 2.1 to (3.21), we can conclude that
. Applying Lemma 2.1 to (3.21), we can conclude that  .
.
Next, we show that  . Note that
. Note that  for each
for each  . Hence, for each
. Hence, for each  and
and  , we obtain
, we obtain

From (A2), we have

Therefore,

For each  and
and  , put
, put  . Then, we have
. Then, we have  . From (3.24), we get that
. From (3.24), we get that

We note that  ,
,  as
as  , and
, and  is a family of monotone mappings. It follows from (3.25) that
is a family of monotone mappings. It follows from (3.25) that

So, by (A1), (A4) and (3.26), we have for each  and
and  that
that

This implies that

Letting  in (3.28), it follows from (A3) that
in (3.28), it follows from (A3) that

Hence  ; consequently,
; consequently,  . Further, we see that
. Further, we see that

So, we have

In particular,

Since  , we have
, we have  as
as  . By using the same argument as in the proof of Theorem 3.1 of [25], we can show that
. By using the same argument as in the proof of Theorem 3.1 of [25], we can show that  as
as  . This completes the proof.
. This completes the proof.
4. Strong Convergence Results
Theorem 4.1.
Let  be a nonempty, closed and convex subset of a real Hilbert space
be a nonempty, closed and convex subset of a real Hilbert space  . Let
. Let  be a family of bifunctions, let
be a family of bifunctions, let  be a family of
be a family of  -inverse-strongly monotone mappings and let
-inverse-strongly monotone mappings and let  be a countable family of
be a countable family of  -strict pseudocontractions for some
-strict pseudocontractions for some  such that
such that  . Assume that
. Assume that  ,
,  ,
,  and
and  for each
for each  satisfy the following conditions:
satisfy the following conditions:
(i) and
and  ,
,
(ii) .
.
Suppose that  satisfies the
satisfies the  -condition. Then,
-condition. Then,  generated by (1.14) converges strongly to an element in
generated by (1.14) converges strongly to an element in  .
.
Proof.
For each  , define
, define  by
by  ,
,  . Then,
. Then,  , since
, since  . Moreover, we know that
. Moreover, we know that  satisfies the
satisfies the  -condition, since
-condition, since  satisfies the
satisfies the  -condition. By Lemma 2.5, we can define the mapping
-condition. By Lemma 2.5, we can define the mapping  by
by  for
for  . Hence,
. Hence,  ,
,  , since
, since  for
for  . Further, we know that
. Further, we know that  is nonexpansive for each
is nonexpansive for each  . Indeed, for each
. Indeed, for each  and
and  , we have
, we have

Hence,  is nonexpansive for each
is nonexpansive for each  and so is
and so is  .
.
Next, we show that  is bounded. Denote
is bounded. Denote  for any
for any  and
and  . We note that
. We note that  . From (1.14), we have for each
. From (1.14), we have for each  that
that

Hence, by induction,  is bounded and so are
is bounded and so are  and
and  .
.
Next, we show that

Since  and
and  ,
,

Set  ,
,  . So, we have from (1.14) and (4.4) that
. So, we have from (1.14) and (4.4) that

Since  satisfies the
satisfies the  -condition and
-condition and  , it follows that
, it follows that

So, by Lemma 2.2 and (ii), we obtain

Hence,

Observe that

as  . Similar to the proof of Theorem 3.1, we obtain for each
. Similar to the proof of Theorem 3.1, we obtain for each  that
that


for some  and
and  . Then, from (4.10), we have
. Then, from (4.10), we have

which implies that

So, from (4.8), (i), (ii) and  for each
for each  , we have
, we have

for each  . Similarly, from (4.11), we have
. Similarly, from (4.11), we have

This implies that

From (i), (ii), (4.8), and (4.14), it follows that

for each  .
.
Next, we show that

Observing

it follows, by (4.17), that

From (4.9) and (4.20), we have

We see that

So, by (4.7), (4.21), and Lemma 2.5, we have

Let the net  be defined by (3.3). By Theorem 3.1, we have
be defined by (3.3). By Theorem 3.1, we have  as
as  . Moreover, by proving in the same manner as in Theorem 3.2 of [25], we can show that
. Moreover, by proving in the same manner as in Theorem 3.2 of [25], we can show that

Finally, we show that  as
as  . From (1.14), we have
. From (1.14), we have

By (i) and (4.24), it follows from Lemma 2.3 that  . This completes the proof.
. This completes the proof.
As a direct consequence of Lemmas 2.6 and 2.7 and Theorem 4.1, we obtain the following result.
Theorem 4.2.
Let  be a nonempty, closed, and convex subset of a real Hilbert space
be a nonempty, closed, and convex subset of a real Hilbert space  . Let
. Let  be a family of bifunctions, let
be a family of bifunctions, let  be a family of
be a family of  -inverse-strongly monotone mappings, and let
-inverse-strongly monotone mappings, and let  be a sequence of
be a sequence of  -strict pseudocontractions of
-strict pseudocontractions of  into itself such that
into itself such that  and
and  . Assume that
. Assume that  and
and  for each
for each  . Define the sequence
. Define the sequence  by
by  and
and

where  and
and  are real sequences in
are real sequences in  which satisfy (i)-(ii) of Theorem 4.1 and
which satisfy (i)-(ii) of Theorem 4.1 and  is a real sequence which satisfies (i)–(iii) of Lemma 2.7. Then,
is a real sequence which satisfies (i)–(iii) of Lemma 2.7. Then,  converges strongly to an element in
converges strongly to an element in  .
.
Remark 4.3.
Theorems 4.1 and 4.2 extend the main results in [25] from a nonexpansive mapping to an infinite family of strict pseudocontractions and a system of generalized equilibrium problems.
Remark 4.4.
If we take  and
and  for each
for each  , then Theorems 3.1, 4.1, and 4.2 can be applied to a system of equilibrium problems and to a system of variational inequality problems, respectively.
, then Theorems 3.1, 4.1, and 4.2 can be applied to a system of equilibrium problems and to a system of variational inequality problems, respectively.
Remark 4.5.
Let  be an infinite family of nonexpansive mappings of
be an infinite family of nonexpansive mappings of  into itself, and let
into itself, and let  be real numbers such that
be real numbers such that  for all
for all  . Moreover, let
. Moreover, let  and
and  be the
be the  -mappings [35] generated by
-mappings [35] generated by  and
and  and
and  and
and  . Then, we know from [7, 35] that
. Then, we know from [7, 35] that  satisfies the
satisfies the  -condition. Therefore, in Theorem 4.1, the mapping
-condition. Therefore, in Theorem 4.1, the mapping  can be also replaced by
can be also replaced by  .
.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Moudafi A, Théra M: Proximal and dynamical approaches to equilibrium problems. In Ill-Posed Variational Problems and Regularization Techniques, Lecture Notes in Economics and Mathematical Systems. Volume 477. Springer, Berlin, Germany; 1999:187–201.
Colao V, Acedo GL, Marino G: An implicit method for finding common solutions of variational inequalities and systems of equilibrium problems and fixed points of infinite family of nonexpansive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7–8):2708–2715. 10.1016/j.na.2009.01.115
Cholamjiak P, Suantai S: Convergence analysis for a system of equilibrium problems and a countable family of relatively quasi-nonexpansive mappings in Banach spaces. Abstract and Applied Analysis 2010, 2010:-17.
Jaiboon C: The hybrid steepest descent method for addressing fixed point problems and system of equilibrium problems. Thai Journal of Mathematics 2010, 8: 275–292.
Jitpeera T, Kumam P: An extragradient type method for a system of equilibrium problems, variational inequality problems and fixed points of finitely many nonexpansive mappings. Journal of Nonlinear Analysis and Optimization 2010, 1: 71–91.
Peng J-W, Yao J-C: A viscosity approximation scheme for system of equilibrium problems, nonexpansive mappings and monotone mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,71(12):6001–6010. 10.1016/j.na.2009.05.028
Marino G, Xu H-K: Weak and strong convergence theorems for strict pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2007,329(1):336–346. 10.1016/j.jmaa.2006.06.055
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Reich S: Weak convergence theorems for nonexpansive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1979,67(2):274–276. 10.1016/0022-247X(79)90024-6
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Zhou H: Convergence theorems of fixed points for Lipschitz pseudo-contractions in Hilbert spaces. Journal of Mathematical Analysis and Applications 2008,343(1):546–556. 10.1016/j.jmaa.2008.01.045
Acedo GL, Xu HK: Iterative methods for strict pseudo-contractions in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2007,67(7):2258–2271. 10.1016/j.na.2006.08.036
Ceng LC, Shyu DS, Yao JC: Relaxed composite implicit iteration process for common fixed points of a finite family of strictly pseudocontractive mappings. Fixed Point Theory and Applications 2009, 2009:-16.
Ceng L-C, Petruşel A, Yao J-C: Strong convergence of modified implicit iterative algorithms with perturbed mappings for continuous pseudocontractive mappings. Applied Mathematics and Computation 2009,209(2):162–176. 10.1016/j.amc.2008.10.062
Ceng L-C, Al-Homidan S, Ansari QH, Yao J-C: An iterative scheme for equilibrium problems and fixed point problems of strict pseudo-contraction mappings. Journal of Computational and Applied Mathematics 2009,223(2):967–974. 10.1016/j.cam.2008.03.032
Cholamjiak P, Suantai S: Weak convergence theorems for a countable family of strict pseudocontractions in banach spaces. Fixed Point Theory and Applications 2010, 2010:-16.
Peng J-W, Yao J-C: Ishikawa iterative algorithms for a generalized equilibrium problem and fixed point problems of a pseudo-contraction mapping. Journal of Global Optimization 2010,46(3):331–345. 10.1007/s10898-009-9428-9
Zhang Y, Guo Y: Weak convergence theorems of three iterative methods for strictly pseudocontractive mappings of Browder-Petryshyn type. Fixed Point Theory and Applications 2008, 2008:-13.
Zhang H, Su Y: Convergence theorems for strict pseudo-contractions in
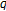 -uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):4572–4580. 10.1016/j.na.2009.03.033
-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):4572–4580. 10.1016/j.na.2009.03.033Zhou H: Convergence theorems for
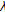 -strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):3160–3173. 10.1016/j.na.2007.09.009
-strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):3160–3173. 10.1016/j.na.2007.09.009Zhou HY: Convergence theorems for
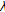 -strict pseudo-contractions in
-strict pseudo-contractions in 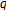 -uniformly smooth Banach spaces. Acta Mathematica Sinica 2010,26(4):743–758. 10.1007/s10114-010-7341-2
-uniformly smooth Banach spaces. Acta Mathematica Sinica 2010,26(4):743–758. 10.1007/s10114-010-7341-2Moudafi A: Weak convergence theorems for nonexpansive mappings and equilibrium problems. Journal of Nonlinear and Convex Analysis 2008,9(1):37–43.
Takahashi S, Takahashi W: Strong convergence theorem for a generalized equilibrium problem and a nonexpansive mapping in a Hilbert space. Nonlinear Analysis: Theory, Methods & Applications 2008,69(3):1025–1033. 10.1016/j.na.2008.02.042
Yao Y, Liou YC, Marino G: Strong convergence of two iterative algorithms for nonexpansive mappings in Hilbert spaces. Fixed Point Theory and Applications 2009, 2009:-7.
Combettes PL, Hirstoaga SA: Equilibrium programming in Hilbert spaces. Journal of Nonlinear and Convex Analysis 2005,6(1):117–136.
Browder FE: Nonexpansive nonlinear operators in a Banach space. Proceedings of the National Academy of Sciences of the United States of America 1965, 54: 1041–1044. 10.1073/pnas.54.4.1041
Goebel K, Kirk WA: Topics in Metric Fixed Point Theory, Cambridge Studies in Advanced Mathematics. Volume 28. Cambridge University Press, Cambridge, UK; 1990:viii+244.
Suzuki T: Strong convergence of Krasnoselskii and Mann's type sequences for one-parameter nonexpansive semigroups without Bochner integrals. Journal of Mathematical Analysis and Applications 2005,305(1):227–239. 10.1016/j.jmaa.2004.11.017
Xu H-K: Iterative algorithms for nonlinear operators. Journal of the London Mathematical Society 2002,66(1):240–256. 10.1112/S0024610702003332
Nadezhkina N, Takahashi W: Weak convergence theorem by an extragradient method for nonexpansive mappings and monotone mappings. Journal of Optimization Theory and Applications 2006,128(1):191–201. 10.1007/s10957-005-7564-z
Aoyama K, Kimura Y, Takahashi W, Toyoda M: Approximation of common fixed points of a countable family of nonexpansive mappings in a Banach space. Nonlinear Analysis: Theory, Methods & Applications 2007,67(8):2350–2360. 10.1016/j.na.2006.08.032
Boonchari D, Saejung S: Weak and strong convergence theorems of an implicit iteration for a countable family of continuous pseudocontractive mappings. Journal of Computational and Applied Mathematics 2009,233(4):1108–1116. 10.1016/j.cam.2009.09.007
Boonchari D, Saejung S: Construction of common fixed points of a countable family of
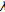 -demicontractive mappings in arbitrary Banach spaces. Applied Mathematics and Computation 2010,216(1):173–178. 10.1016/j.amc.2010.01.027
-demicontractive mappings in arbitrary Banach spaces. Applied Mathematics and Computation 2010,216(1):173–178. 10.1016/j.amc.2010.01.027Shimoji K, Takahashi W: Strong convergence to common fixed points of infinite nonexpansive mappings and applications. Taiwanese Journal of Mathematics 2001,5(2):387–404.
Acknowledgments
The authors would like to thank the referees for valuable suggestions. This research is supported by the Centre of Excellence in Mathematics, the Commission on Higher Education, and the Thailand Research Fund. The first author is supported by the Royal Golden Jubilee Grant no. PHD/0261/2551 and by the Graduate School, Chiang Mai University, Thailand.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Cholamjiak, P., Suantai, S. Convergence Analysis for a System of Generalized Equilibrium Problems and a Countable Family of Strict Pseudocontractions. Fixed Point Theory Appl 2011, 941090 (2011). https://doi.org/10.1155/2011/941090
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/941090
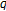 -uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):4572–4580. 10.1016/j.na.2009.03.033
-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):4572–4580. 10.1016/j.na.2009.03.033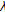 -strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):3160–3173. 10.1016/j.na.2007.09.009
-strict pseudo-contractions in 2-uniformly smooth Banach spaces. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):3160–3173. 10.1016/j.na.2007.09.009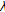 -strict pseudo-contractions in
-strict pseudo-contractions in 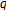 -uniformly smooth Banach spaces. Acta Mathematica Sinica 2010,26(4):743–758. 10.1007/s10114-010-7341-2
-uniformly smooth Banach spaces. Acta Mathematica Sinica 2010,26(4):743–758. 10.1007/s10114-010-7341-2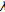 -demicontractive mappings in arbitrary Banach spaces. Applied Mathematics and Computation 2010,216(1):173–178. 10.1016/j.amc.2010.01.027
-demicontractive mappings in arbitrary Banach spaces. Applied Mathematics and Computation 2010,216(1):173–178. 10.1016/j.amc.2010.01.027