- Research Article
- Open access
- Published:
The Existence of Maximum and Minimum Solutions to General Variational Inequalities in the Hilbert Lattices
Fixed Point Theory and Applications volume 2011, Article number: 904320 (2011)
Abstract
We apply the variational characterization of the metric projection to prove some results about the solvability of general variational inequalities and the existence of maximum and minimum solutions to some general variational inequalities in the Hilbert lattices.
1. Introduction
The variational inequality theory and the complementarity theory have been studied by many authors and have been applied in many fields such as optimization theory, game theory, economics, and engineering [1–12]. The existence of solutions to a general variational inequality is the most important issue in the variational inequality theory. Many authors investigate the solvability of a general variational inequality by using the techniques of fixed point theory and the variational characterization of the metric projection in some linear normal spaces. Meanwhile, a certain topological continuity of the mapping involved in the considered variational inequality must be required, such as continuity and semicontinuity.
A number of authors have studied the solvability of general variational inequalities without the topological continuity of the mapping. One way to achieve this goal is to consider a linear normal space to be embedded with a partial order satisfying certain conditions, which is called a normed Riesz space. The special and most important cases of normed Riesz spaces are Hilbert lattices and Banach lattices [1, 2, 7, 13–15]. Furthermore, after the solvability has been proved for a general variational inequality, a new problem has been raised: does this general variational inequality have maximum and minimum solutions (with respect to the partial order)? (e.g., see [7]). In this paper, we study this theme and provide some results about the existence of maximum and minimum solutions to some general variational inequalities in Hilbert lattices.
This paper is organized as follows. Section 2 recalls some basic properties of Hilbert lattices, variational inequalities, and general variational inequalities. Section 3 provides some results about the existence of maximum and minimum solutions to some general variational inequalities defined on some closed, bounded, and convex subsets in Hilbert lattices. Section 4 generalizes the results of Section 3 to unbounded case.
2. Preliminaries
In this section, we recall some basic properties of Hilbert lattices and variational inequalities. For more details, the reader is referred to [1, 2, 7, 13–15].
We say that  is a Hilbert lattice if
is a Hilbert lattice if  is a Hilbert space with inner product
is a Hilbert space with inner product  and with the induced norm
and with the induced norm  and
and  is also a poset with the partial order
is also a poset with the partial order  satisfying the following conditions:
satisfying the following conditions:
(i)the mapping  is a
is a  -preserving self-mapping on
-preserving self-mapping on  (this definition will be recalled later) for every
(this definition will be recalled later) for every  and positive number
and positive number  , where
, where  defines the identical mapping on
defines the identical mapping on  ,
,
(ii) is a lattice,
is a lattice,
-
(iii)
the norm
 on
on 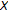 is compatible with the partial order
is compatible with the partial order  , that is,
, that is,

A nonempty subset  of a Hilbert lattice
of a Hilbert lattice  is said to be a subcomplete
is said to be a subcomplete  - sublattice of
- sublattice of  , if for any nonempty subset
, if for any nonempty subset  of
of  ,
,  and
and  . Since every bounded closed convex subset of a Hilbert space is weakly compact, as an immediate consequence of Lemma 2.3 in [7], we have the following result.
. Since every bounded closed convex subset of a Hilbert space is weakly compact, as an immediate consequence of Lemma 2.3 in [7], we have the following result.
Lemma 2.1.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a bounded, closed, and convex
a bounded, closed, and convex  -sublattice of
-sublattice of  . Then,
. Then,  is a subcomplete
is a subcomplete  -sublattice of
-sublattice of  .
.
Now, we recall the  -preserving properties of set-valued mappings below. A set-valued mapping
-preserving properties of set-valued mappings below. A set-valued mapping  is said to be upper
is said to be upper  -preserving, if
-preserving, if  , then for any
, then for any  , there exists
, there exists  such that
such that  . A set-valued mapping
. A set-valued mapping  is said to be lower
is said to be lower  -preserving, if
-preserving, if  , then for any
, then for any  , there exists
, there exists  such that
such that  .
.  is said to be
is said to be  -preserving if it is both of upper and lower
-preserving if it is both of upper and lower  -preserving. Similarly, we can define that
-preserving. Similarly, we can define that  is said to be strictly upper
is said to be strictly upper  -preserving, if
-preserving, if  , then for any
, then for any  , there exists
, there exists  such that
such that  and
and  is said to be strictly (lower
is said to be strictly (lower  -preserving if
-preserving if  , then for any
, then for any  , there exists
, there exists  such that
such that  .
.
Observations
(1)If  is upper
is upper  -preserving, then
-preserving, then  implies
implies  .
.
(2)If  is lower
is lower  -preserving, then
-preserving, then  implies
implies  .
.
Let  be a nonempty, closed, and convex sublattice of
be a nonempty, closed, and convex sublattice of  and
and  a mapping. Let us consider the following variational inequality:
a mapping. Let us consider the following variational inequality:

An element  is called a solution to the variational inequality (2.2) if, for every
is called a solution to the variational inequality (2.2) if, for every  . The problem to find a solution to variational inequality (2.2) is called a variational inequality problem associated with the mapping
. The problem to find a solution to variational inequality (2.2) is called a variational inequality problem associated with the mapping  and the subset
and the subset  , which is denoted by
, which is denoted by  .
.
Let  be a set-valued mapping. The general variational inequality problem associated with the set-valued mapping
be a set-valued mapping. The general variational inequality problem associated with the set-valued mapping  and the subset
and the subset  , which is denoted by
, which is denoted by  , is to find
, is to find  , with some
, with some  , such that
, such that

Let  be the metric projection. Then, we have the well-known variational characterization of the metric projection (e.g., see [7, Lemma 2.5]): if
be the metric projection. Then, we have the well-known variational characterization of the metric projection (e.g., see [7, Lemma 2.5]): if  is a nonempty, closed, and convex sublattice of a Hilbert lattice
is a nonempty, closed, and convex sublattice of a Hilbert lattice  , then an element
, then an element  is a solution to
is a solution to  if and only if
if and only if

Similarly, we can have the representation of a solution to a  , defined by (2.3), by a fixed point as given by relation (2.4).
, defined by (2.3), by a fixed point as given by relation (2.4).
3. The Existence of Maximum and Minimum Solutions to Some General Variational Inequalities Defined on Closed, Bounded, and Convex Subsets in Hilbert Lattices
In this section, we apply the variational characterization of the metric projection in Hilbert spaces to study the solvability of general variational inequalities without the continuity of the mappings involved in the considered general variational inequalities. Then, we provide some results about the existence of maximum and minimum solutions to some general variational inequalities defined on some closed, bounded, and convex subsets in Hilbert lattices. Similar to the conditions used by Smithson [15], we need the following definitions.
Let  be a nonempty subset of a Hilbert lattice
be a nonempty subset of a Hilbert lattice  and
and  a set-valued correspondence.
a set-valued correspondence.  is said to be upper (lower)
is said to be upper (lower)  -bound if there exists
-bound if there exists  , such that
, such that  exists and
exists and

 is said to have upper (lower) bound
is said to have upper (lower) bound  -closed values, if for all
-closed values, if for all  , we have
, we have

Remarks
Let  be a nonempty subset of a Hilbert lattice
be a nonempty subset of a Hilbert lattice  ,
,  a set-valued correspondence. Then, we have the following.
a set-valued correspondence. Then, we have the following.
(1)If subset  is upper
is upper  -bound
-bound  -closed and
-closed and  is upper
is upper  -preserving, then
-preserving, then  is upper
is upper  -bound and
-bound and

(2)If subset  is lower
is lower  -bound
-bound  -closed and
-closed and  is lower
is lower  -preserving, then
-preserving, then  is lower
is lower  -bound and
-bound and

(3)If  is strictly upper
is strictly upper  -preserving and has upper bound
-preserving and has upper bound  -closed values, then
-closed values, then

(4)If  is strictly lower
is strictly lower  -preserving and has lower bound
-preserving and has lower bound  -closed values, then
-closed values, then

Now, we state and prove the main theorem of this paper below, which provides the existence of maximum and minimum solutions to general variational inequalities in Hilbert lattices.
Theorem 3.1.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a nonempty closed bounded and convex
a nonempty closed bounded and convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. Then, one has
be a set-valued correspondence. Then, one has
(1)if  is upper
is upper  -preserving with upper bound
-preserving with upper bound  -closed values for some function
-closed values for some function  , then the problem
, then the problem  is solvable and there exists
is solvable and there exists  -maximum solution to
-maximum solution to  ,
,
(2)if  is lower
is lower  -preserving with lower bound
-preserving with lower bound  -closed values for some function
-closed values for some function  , then the problem
, then the problem  is solvable and there exists
is solvable and there exists  -minimum solution to
-minimum solution to  ,
,
(3)if  is
is  -preserving with both of upper and lower bounds
-preserving with both of upper and lower bounds  -closed values for some function
-closed values for some function  , then the problem
, then the problem  is solvable and there exist both of
is solvable and there exist both of  -minimum and
-minimum and  -maximum solutions to
-maximum solutions to  .
.
Proof of Theorem 3.1.
Part (1)
From (2.4), the representations of the solutions to  by fixed points of a projection
by fixed points of a projection  , we have that
, we have that  is a solution to
is a solution to  if, and only if, there exists
if, and only if, there exists  such that
such that

Lemma 2.4 in [7] shows that the projection  is
is  -preserving. As a composition of upper
-preserving. As a composition of upper  -preserving mappings, so
-preserving mappings, so  is also an upper
is also an upper  -preserving mapping. From Corollary 1.8 in Smithson [15] and the variational characterization of the metric projection (3.7), we have that the problem
-preserving mapping. From Corollary 1.8 in Smithson [15] and the variational characterization of the metric projection (3.7), we have that the problem  is solvable. Let
is solvable. Let  denote the set of solutions to the problem
denote the set of solutions to the problem  . Then,
. Then,  . Since
. Since  is a nonempty closed bounded and convex
is a nonempty closed bounded and convex  -sublattice of a Hilbert lattice
-sublattice of a Hilbert lattice  , it is weakly compact. From Corollary 2.3 in [7],
, it is weakly compact. From Corollary 2.3 in [7],  is a subcomplete
is a subcomplete  -sublattice of
-sublattice of  . Hence,
. Hence,  . Denote
. Denote

Let

Then, from (3.8) and (3.9), we have

The first  -inequality in (3.10) is based on
-inequality in (3.10) is based on  and the property that the correspondence
and the property that the correspondence  is upper
is upper  -preserving. The second
-preserving. The second  -inequality in (3.10) follows from
-inequality in (3.10) follows from  and the fact that
and the fact that  is upper
is upper  -preserving. The third
-preserving. The third  -inequality in (3.10) follows from the fact that
-inequality in (3.10) follows from the fact that  . Then, we define
. Then, we define

From (3.10),  , applying the upper
, applying the upper  -preserving property of the mapping
-preserving property of the mapping  again, we get
again, we get

that is,  . Denote
. Denote

From the upper  -preserving property of
-preserving property of  , we obtain
, we obtain

which implies

From (3.9)−(3.11), it is clear that  , and therefore,
, and therefore,  . Define
. Define

It holds that

From the upper  -preserving property of the mapping
-preserving property of the mapping  again, we have
again, we have

Applying (3.16), it implies

It is obvious that  , so
, so  . From (3.15), we have
. From (3.15), we have

Then, (3.20), (3.16), and (3.19) together imply

From the assumption that  , we get
, we get

Hence,  . Then, the relation
. Then, the relation  and (3.8) imply
and (3.8) imply  . Thus,
. Thus,

It completes the proof of part (1) of this theorem.
Part (2)
Very similar to the proof of part (1), we can prove the second part of this theorem. Denote

From the proof of part (1), we see that  . We need to prove
. We need to prove  . Let
. Let

Then, we have

The first-order inequality in (3.26) is based on  (piecewise) and the property that the correspondence
(piecewise) and the property that the correspondence  is lower
is lower  -preserving, which is the composition of the
-preserving, which is the composition of the  -preserving map
-preserving map  and a lower
and a lower  -preserving map
-preserving map  (condition 2 in this theorem). The second-order inequality in (3.26) follows from the definition of
(condition 2 in this theorem). The second-order inequality in (3.26) follows from the definition of  in (3.24) and the fact that
in (3.24) and the fact that  ; it is because
; it is because  . Then, we define
. Then, we define

From (3.26),  , the lower
, the lower  -preserving of
-preserving of  , and the Observation part
, and the Observation part  in last section, we get
in last section, we get

that is,  . Denote
. Denote

From the lower  -preserving property of
-preserving property of  , we obtain
, we obtain

which implies

From (3.24)−(3.27), it is clear that  , and therefore,
, and therefore,  . Define
. Define

that is,

From the lower  -preserving property of the mapping
-preserving property of the mapping  again, we have
again, we have

Applying (3.32), it implies

It is obvious that  , so
, so  . From (3.35), we have
. From (3.35), we have

Then, (3.36), (3.32), and (3.35) together imply

From the assumption that  , we get
, we get

Hence,  . Then, the relation
. Then, the relation  and (3.24) imply
and (3.24) imply  . Thus,
. Thus,

It completes the proof of part (2) of this theorem. Part (3) is an immediate consequence of parts (1) and (2). It completes the proof of Theorem 3.1.
If  is a single-valued mapping, then it can be considered as a special case of set-valued mapping with singleton values. The result below follows immediately from Theorem 3.1.
is a single-valued mapping, then it can be considered as a special case of set-valued mapping with singleton values. The result below follows immediately from Theorem 3.1.
Corollary 3.2.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a nonempty closed, bounded, and convex
a nonempty closed, bounded, and convex  -sublattice of
-sublattice of  . Let
. Let  be a single-valued mapping such that
be a single-valued mapping such that  is
is  -preserving, for some function
-preserving, for some function  . Then, one has
. Then, one has
(1)the problem  is solvable,
is solvable,
(2)there are both of  -maximum and
-maximum and  -minimum solutions to
-minimum solutions to  .
.
For a bounded and convex  -sublattice of a Hilbert lattice
-sublattice of a Hilbert lattice  , the behavior of its maximum and minimum solutions to a problem
, the behavior of its maximum and minimum solutions to a problem  should be noticeable. The following corollary can be obtained from the proof of Theorem 3.1.
should be noticeable. The following corollary can be obtained from the proof of Theorem 3.1.
Corollary 3.3.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a nonempty, closed, bounded, and convex
a nonempty, closed, bounded, and convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. Then, the following properties hold.
be a set-valued correspondence. Then, the following properties hold.
(1)Assume that  is upper
is upper  -preserving for some function
-preserving for some function  , and has upper bound
, and has upper bound  -closed values. Let
-closed values. Let  be the set of solutions to
be the set of solutions to  , then
, then

(2)Assume that  is lower
is lower  -preserving for some function
-preserving for some function  , and has lower bound
, and has lower bound  -closed values. Then,
-closed values. Then,

Proof of Corollary 3.3.
Part (1)
In the proof of part (1) of Theorem 3.1, we have

It implies

From the definition of  in (3.8), we get
in (3.8), we get

Similar to the proof of part (2) of Theorem 3.1, we can prove Part (2) of this corollary.
The following corollary is an immediate consequence of Corollary 3.3.
Corollary 3.4.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a nonempty, closed, bounded, and convex
a nonempty, closed, bounded, and convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. Then, the following properties hold.
be a set-valued correspondence. Then, the following properties hold.
(1)Assume that  is upper
is upper  -preserving for some function
-preserving for some function  , and has upper bound
, and has upper bound  -closed value at point
-closed value at point  . If
. If  is a solution to
is a solution to  , then
, then

(2)Suppose that  is lower
is lower  -preserving for some function
-preserving for some function  , and has lower bound
, and has lower bound  -closed value at point
-closed value at point  . If
. If  is a solution to
is a solution to  , then
, then

Proof of Corollary 3.4.
Part (1)
If  is a solution to
is a solution to  , then we must have
, then we must have

Substituting it into part (1) of Corollary 3.3, we get

The first part is proved. Similarly, the second part can be proved.
In Theorem 3.1, without the upper bound  -closed condition for the values of the mapping
-closed condition for the values of the mapping  , Theorem 3.1 may be failed, that is, if
, Theorem 3.1 may be failed, that is, if  is upper
is upper  -preserving that has no upper bound
-preserving that has no upper bound  -closed values for some function
-closed values for some function  , then, there may not exist a
, then, there may not exist a  -maximum solution to
-maximum solution to  . The following example demonstrates this argument.
. The following example demonstrates this argument.
Example 3.5.
Take  . Define the partial order
. Define the partial order  as follows:
as follows:

Then,  is a Hilbert lattice with the normal inner product in
is a Hilbert lattice with the normal inner product in  and the above partial order
and the above partial order  .
.
Let  be the closed rhomb with vertexes
be the closed rhomb with vertexes  ,
,  ,
,  , and
, and  . Then,
. Then,  is a compact (of course weakly compact) and convex
is a compact (of course weakly compact) and convex  -sublattice of
-sublattice of  .
.
Take  and define
and define  as follows:
as follows:

Then,  is a set-valued mapping with compact values. From the definitions of
is a set-valued mapping with compact values. From the definitions of  and
and  , we have
, we have

We can see that  is an upper
is an upper  -preserving correspondence (in fact, it is both of upper
-preserving correspondence (in fact, it is both of upper  -preserving and lower
-preserving and lower  -preserving) and
-preserving) and  has no upper bound
has no upper bound  -closed values. One can check that the mapping
-closed values. One can check that the mapping  has the set of fixed points below
has the set of fixed points below

which is the set of solutions to  . It is clear that
. It is clear that

But, the point  is not a solutions to
is not a solutions to  , which shows that there does not exist a
, which shows that there does not exist a  -maximum solution to this problem
-maximum solution to this problem  .
.
Similarly, in Theorem 3.1, without the lower bound  -closed condition for the values of the mapping
-closed condition for the values of the mapping  , then Theorem 3.1 (part (2)) may be failed. That is, if
, then Theorem 3.1 (part (2)) may be failed. That is, if  is lower
is lower  -preserving that has no lower bound
-preserving that has no lower bound  -closed values for some function
-closed values for some function  , then there may not exist a
, then there may not exist a  -minimum solution to
-minimum solution to  . This can be demonstrated by the following example.
. This can be demonstrated by the following example.
Example 3.6.
Take  as in Example 3.5. Let
as in Example 3.5. Let  be the closed rhomb with vertexes
be the closed rhomb with vertexes  ,
,  ,
,  , and
, and  . Then,
. Then,  is a compact (of course weakly compact) and convex
is a compact (of course weakly compact) and convex  -sublattice of
-sublattice of  .
.
Take  and define
and define  exactly the same as that in the proof of part (1)
exactly the same as that in the proof of part (1)

We also have

which is the set of solutions to  . It is clear that
. It is clear that

But,  is not a solutions to
is not a solutions to  , which shows that there does not exist a
, which shows that there does not exist a  -minimum solution to this problem
-minimum solution to this problem  .
.
Suppose that  is upper (lower)
is upper (lower)  -preserving. The condition that
-preserving. The condition that  has upper (lower) bound
has upper (lower) bound  -closed values for some function
-closed values for some function  , is not necessary for the problem
, is not necessary for the problem  to have a
to have a  -maximum (minimum) solution to
-maximum (minimum) solution to  . The following example was given by Nishimura and Ok.
. The following example was given by Nishimura and Ok.
Example 3.7.
Take  as in Example 3.5. Let
as in Example 3.5. Let  . Define
. Define

Take  . Then,
. Then,  is upper
is upper  -preserving.
-preserving.  has a unique solution
has a unique solution  , which is also the
, which is also the  -maximum solution to
-maximum solution to  . But
. But  does not have upper bound
does not have upper bound  -closed values (except at point
-closed values (except at point  ).
).
Example 3.7 leads us to consider some conditions on the mapping  that are weaker than that in Theorem 3.1 which still guarantees the existence of a
that are weaker than that in Theorem 3.1 which still guarantees the existence of a  -maximum (minimum) solution to
-maximum (minimum) solution to  . To achieve this goal, we have the following notations. Let
. To achieve this goal, we have the following notations. Let  be a Hilbert lattice and
be a Hilbert lattice and  a bounded and convex
a bounded and convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. An element
be a set-valued correspondence. An element  is said to be nondescending (nonascending) with respect to the mapping
is said to be nondescending (nonascending) with respect to the mapping  if
if

for some function  .
.
Applying the  -preserving property of
-preserving property of  , for every
, for every  , we have
, we have

If  is upper
is upper  -preserving (lower
-preserving (lower  -preserving), then from the upper (lower)
-preserving), then from the upper (lower)  -preserving property of the mapping
-preserving property of the mapping  , we have
, we have

The properties in (3.60) imply that, under the condition  is upper
is upper  -preserving (lower
-preserving (lower  -preserving), if an element
-preserving), if an element  is nonascending (nonascending) with respect to the mapping
is nonascending (nonascending) with respect to the mapping  , then
, then  is nondescending (nonascending) with respect to the mapping
is nondescending (nonascending) with respect to the mapping  .
.
Definition 3.8.
For every  , we denote
, we denote

A point  is said to be an upper (lower) absorbing point with respect to a set-valued mapping
is said to be an upper (lower) absorbing point with respect to a set-valued mapping  , if there exists
, if there exists  with
with  such that
such that  .
.
The following proposition describes some existence and uniqueness properties of upper (lower) absorbing point with respect to a set-valued mapping  .
.
Theorem 3.9.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a subcomplete
a subcomplete  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. Then, the set of upper (lower) absorbing point with respect to the mapping
be a set-valued correspondence. Then, the set of upper (lower) absorbing point with respect to the mapping  is not empty. In addition, if
is not empty. In addition, if  is upper (lower)
is upper (lower)  -preserving, for some function
-preserving, for some function  , then upper (lower) absorbing point with respect to the mapping
, then upper (lower) absorbing point with respect to the mapping  is unique.
is unique.
Proof.
Since  is a subcomplete
is a subcomplete  -sublattice of
-sublattice of  , it contains minimum
, it contains minimum  (maximum
(maximum  ). It is clear that
). It is clear that  ), which implies
), which implies  . Let
. Let  . Since
. Since  is a subcomplete
is a subcomplete  -sublattice of
-sublattice of  , so
, so  . It implies that
. It implies that  is an upper (lower) absorbing point with respect to the mapping
is an upper (lower) absorbing point with respect to the mapping  .
.
In addition, suppose that  is upper (lower)
is upper (lower)  -preserving, for some function
-preserving, for some function  , we prove that
, we prove that  is the unique upper (lower) absorbing point with respect to the mapping
is the unique upper (lower) absorbing point with respect to the mapping  . Assume that
. Assume that  is an upper (lower) absorbing point with respect to the mapping
is an upper (lower) absorbing point with respect to the mapping  , such that
, such that  ), for some
), for some  . It is clear that
. It is clear that  ) which implies
) which implies

On the other hand, similar to the proof of (3.10), we have

where the second  -inequality in (3.63) follows from the definitions of
-inequality in (3.63) follows from the definitions of  and
and  , that contain all nonascending with respect to the mapping
, that contain all nonascending with respect to the mapping  greater than
greater than  ,
,  , respectively. The
, respectively. The  -inequalities (3.63) implies
-inequalities (3.63) implies  is nonascending with respect to the mapping
is nonascending with respect to the mapping  . It is clear that
. It is clear that  , and, therefore,
, and, therefore,  . The definition
. The definition  implies
implies

Combining (3.62) and (3.64), we get  (similar to (3.62) and (3.64), we can prove
(similar to (3.62) and (3.64), we can prove  ). It shows the uniqueness of upper (lower) absorbing point with respect to the mapping
). It shows the uniqueness of upper (lower) absorbing point with respect to the mapping  . The proposition is proved.
. The proposition is proved.
Now, we apply the concepts of absorbing points with respect to a mapping to extend Theorem 3.1 to the following theorem with conditions that are weaker than those in Theorem 3.1.
Theorem 3.10.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a nonempty, closed, bounded, and convex
a nonempty, closed, bounded, and convex  - sublattice of
- sublattice of  . Let
. Let be a set-valued correspondence. Then, one has
be a set-valued correspondence. Then, one has
(1)if  is upper
is upper  -preserving with upper bound
-preserving with upper bound  -closed value at the unique upper absorbing point with respect to the mapping
-closed value at the unique upper absorbing point with respect to the mapping  , for some function
, for some function  , then the problem
, then the problem  is solvable and the unique upper absorbing point with respect to the mapping
is solvable and the unique upper absorbing point with respect to the mapping  is a solution to
is a solution to  ,
,
(2)if  is lower
is lower  -preserving with lower bound
-preserving with lower bound  -closed value at the unique lower absorbing points with respect to the mapping
-closed value at the unique lower absorbing points with respect to the mapping  , for some function
, for some function  , then the problem
, then the problem  is solvable and the unique lower absorbing point with respect to the mapping
is solvable and the unique lower absorbing point with respect to the mapping  is a solution to
is a solution to  .
.
Proof of Theorem 3.10.
Part (1)
Since (as in the proof of Theorem 3.1)  is a subcomplete
is a subcomplete  -sublattice of
-sublattice of  . From Theorem 3.9,
. From Theorem 3.9,  is the unique upper absorbing point with respect to the mapping
is the unique upper absorbing point with respect to the mapping  , where
, where  is the minimum of
is the minimum of  . The assumptions of Part (1) imply
. The assumptions of Part (1) imply

From the upper  -preserving property of
-preserving property of  , the equation
, the equation  , and the definition of
, and the definition of  , we get
, we get

which implies

Since  , the
, the  -inequality (3.67) implies that
-inequality (3.67) implies that  is nonascending with respect to the mapping
is nonascending with respect to the mapping  , and, therefore,
, and, therefore,

Applying the property (3.60) that if  is nonascending with respect to a mapping
is nonascending with respect to a mapping  satisfying that
satisfying that  is upper
is upper  -preserving, for some function
-preserving, for some function  , then so is
, then so is  , from (3.67) and (3.68), it yields
, from (3.67) and (3.68), it yields

The definition  , the above relation, and (3.67) together imply
, the above relation, and (3.67) together imply

From (3.65) and the above equation, we obtain that the unique upper absorbing point with respect to the mapping 
 is a solution to
is a solution to  . Then, the solvability of the problem
. Then, the solvability of the problem  is proved. It completes the proof of part (1).
is proved. It completes the proof of part (1).
Similar to the proof of part (1), we can prove Part (2).
Theorem 3.11.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a nonempty, closed, bounded, and convex
a nonempty, closed, bounded, and convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. Then, one has
be a set-valued correspondence. Then, one has
(1)if  is upper
is upper  -preserving with upper bound
-preserving with upper bound  -closed value at the unique upper absorbing point with respect to the mapping
-closed value at the unique upper absorbing point with respect to the mapping  , for some function
, for some function  , then the unique upper absorbing point is the
, then the unique upper absorbing point is the  -maximum solution to
-maximum solution to  ,
,
(2)if  is lower
is lower  -preserving with lower bound
-preserving with lower bound  -closed value at the unique lower absorbing point with respect to the mapping
-closed value at the unique lower absorbing point with respect to the mapping  , for some function
, for some function  , then the unique lower absorbing point is the
, then the unique lower absorbing point is the  -minimum solution to
-minimum solution to  ,
,
(3)if  is
is  -preserving with both of upper and lower bounds
-preserving with both of upper and lower bounds  -closed value at the unique upper absorbing point and the unique lower absorbing point with respect to the mapping
-closed value at the unique upper absorbing point and the unique lower absorbing point with respect to the mapping  in
in  , for some function
, for some function  , then the unique upper absorbing point and the unique lower absorbing point are the
, then the unique upper absorbing point and the unique lower absorbing point are the  -maximum and
-maximum and  -minimum solutions to
-minimum solutions to  , respectively.
, respectively.
Proof of Theorem 3.11.
Part (1)
Let  denote the set of solutions to the problem
denote the set of solutions to the problem  . From Theorem 3.10, we have
. From Theorem 3.10, we have  . Since
. Since  is a subcomplete
is a subcomplete  -sublattice of
-sublattice of  ,
,  . Denote
. Denote

Then, similar to (3.10) in the proof of Theorem 3.1, we can show

It implies  . Let
. Let

Then,  is the unique upper absorbing point in
is the unique upper absorbing point in  with respect to the mapping
with respect to the mapping  . From the Part (1) of Theorem 3.10 that the unique upper absorbing point with respect to the mapping
. From the Part (1) of Theorem 3.10 that the unique upper absorbing point with respect to the mapping  is a solution to the problem
is a solution to the problem  , we obtain that
, we obtain that  . Combining the definition
. Combining the definition  and the
and the  -inequality (3.73), we get
-inequality (3.73), we get  . Hence,
. Hence,  is a solution to
is a solution to  , and therefore the problem
, and therefore the problem  has a maximum solution. Part (1) of this theorem is proved. Part (2) can be similarly proved. Part (3) is an immediate consequence of Part (1) and Part (2). This theorem is proved.
has a maximum solution. Part (1) of this theorem is proved. Part (2) can be similarly proved. Part (3) is an immediate consequence of Part (1) and Part (2). This theorem is proved.
Notice that in Example 3.7, the conditions of Theorem 3.1 are not satisfied, that is,  does not have upper bound
does not have upper bound  -closed value at every point (except at point
-closed value at every point (except at point  ). But there exists a
). But there exists a  -maximum solution to
-maximum solution to  in Example 3.7. On the other hand, in Example 3.7, there is a unique upper absorbing point for the mapping
in Example 3.7. On the other hand, in Example 3.7, there is a unique upper absorbing point for the mapping  , which is
, which is  . It satisfies
. It satisfies

that is,

Hence, Example 3.7 satisfies the conditions of Theorem 3.10 (Part (1)), and therefore there exists a  -maximum solution to
-maximum solution to  , which coincides with the result of Example 3.7.
, which coincides with the result of Example 3.7.
Remark 3.12.
Theorem 3.1 is a special case of Theorem 3.10.
4. The Existence of Maximum and Minimum Solutions to Some General Variational Inequalities Defined on Unbounded Subsets in Hilbert Lattices
The difficulty to extend the results in bounded subsets in Hilbert lattices to unbounded subsets in Hilbert lattices is that the subcomplete property of unbounded closed convex  -sublattice of a Hilbert lattice
-sublattice of a Hilbert lattice  does not hold. All the proofs of Theorems 3.1–3.10 in last section are based on the property that any bounded closed convex
does not hold. All the proofs of Theorems 3.1–3.10 in last section are based on the property that any bounded closed convex  -sublattice in Hilbert lattices is a subcomplete
-sublattice in Hilbert lattices is a subcomplete  -sublattice. So, the techniques in those proofs are not applicable in the unbounded case. Hence, except new techniques are developed in unbounded case, we have to apply the results in last section to investigate the solvability of some
-sublattice. So, the techniques in those proofs are not applicable in the unbounded case. Hence, except new techniques are developed in unbounded case, we have to apply the results in last section to investigate the solvability of some  problems. The following results are similar to Theorem 3.3 in [7] and Smithson Theorem 1.1 in [15].
problems. The following results are similar to Theorem 3.3 in [7] and Smithson Theorem 1.1 in [15].
Theorem 4.1.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a closed convex
a closed convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. Suppose that
be a set-valued correspondence. Suppose that  is upper
is upper  -preserving with upper bound
-preserving with upper bound  -closed values at all points in
-closed values at all points in  , for some function
, for some function  . In addition, assume
. In addition, assume
(i) is
is  -preserving and there exist
-preserving and there exist  ,
,  with
with  and
and  , or
, or
(ii) has a
has a  -minimum and there exists
-minimum and there exists  with
with  .
.
Then,  is solvable.
is solvable.
Proof of Theorem 4.1.
Part (i)
Set

Then,  is
is  -bounded closed convex
-bounded closed convex  -sublattice of
-sublattice of  . Then, from [7, Lemma 2.2]), it is a subcomplete
. Then, from [7, Lemma 2.2]), it is a subcomplete  -sublattice of
-sublattice of  . Similar to the proof of Theorem 3.3 in [7] or the proof of Theorem 1.1 in [15], we can show that under the conditions of part (i), the following
. Similar to the proof of Theorem 3.3 in [7] or the proof of Theorem 1.1 in [15], we can show that under the conditions of part (i), the following  -inequalities hold:
-inequalities hold:

which imply

It is clear that  satisfies all conditions of Theorem 3.1 and
satisfies all conditions of Theorem 3.1 and  is a subcomplete
is a subcomplete  -sublattice of
-sublattice of  . Notice that the only application of the nonempty closed bounded condition in Theorem 3.1 in the proof of Theorem 3.1 is to guarantee that the subset is a subcomplete
. Notice that the only application of the nonempty closed bounded condition in Theorem 3.1 in the proof of Theorem 3.1 is to guarantee that the subset is a subcomplete  -sublattice of
-sublattice of  . Here, the subset
. Here, the subset  has been showed to be a subcomplete
has been showed to be a subcomplete  -sublattice of
-sublattice of  . So, applying Theorem 3.1, the problem
. So, applying Theorem 3.1, the problem  is solvable and it has a maximum solution. Let
is solvable and it has a maximum solution. Let  be a solution to
be a solution to  . Then,
. Then,

Since  , we have (piecewise)
, we have (piecewise)

From (4.4), there exists  ) such that
) such that  . Since
. Since  , so
, so  . Using (4.5), from
. Using (4.5), from  , we get
, we get

Since  (from (4.3)), the above inequality implies
(from (4.3)), the above inequality implies  , that is,
, that is,  . Hence,
. Hence,  is a solution to
is a solution to  . Part (i) is proved.
. Part (i) is proved.
Part (ii)
Take  to be the minimum of
to be the minimum of  . The inequality
. The inequality  can be proved by the condition
can be proved by the condition  in part (ii). It is obvious that the inequality
in part (ii). It is obvious that the inequality  holds, because
holds, because  is the minimum of
is the minimum of  . Then, (4.3) can be proved for part (ii) and the rest of the proof will be the same as that in the proof of part (i). It completes the proof of this theorem.
. Then, (4.3) can be proved for part (ii) and the rest of the proof will be the same as that in the proof of part (i). It completes the proof of this theorem.
Theorem 4.2.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a closed convex
a closed convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. Suppose that
be a set-valued correspondence. Suppose that  is upper (lower)
is upper (lower)  -preserving with upper (lower) bound
-preserving with upper (lower) bound  -closed values at all points in
-closed values at all points in  , for some function
, for some function  . In addition, assume that
. In addition, assume that  is a
is a  -bounded closed
-bounded closed  -sublattice of
-sublattice of  . Then,
. Then,  is solvable and it has a maximum (minimum) solution.
is solvable and it has a maximum (minimum) solution.
Proof.
Let  and
and  . Then, the
. Then, the  -preserving property of
-preserving property of  implies
implies

Define

that is,

It is easy to see that  is a
is a  -bounded
-bounded  -sublattice of
-sublattice of  . Then, from Lemma 2.2 in [7],
. Then, from Lemma 2.2 in [7],  is a subcomplete
is a subcomplete  -sublattice of
-sublattice of  containing the set
containing the set  . It is clear that
. It is clear that  .We see that
.We see that  satisfies all conditions of Theorem 3.1. Similar to the proof of Theorem 4.1, from Theorem 3.1, the problem
satisfies all conditions of Theorem 3.1. Similar to the proof of Theorem 4.1, from Theorem 3.1, the problem  is solvable. Let
is solvable. Let  be a solution to
be a solution to  . Then, the proof that
. Then, the proof that  is a solution to
is a solution to  is exactly the same as that in Theorem 4.1. Moreover, the maximum solution to the problem
is exactly the same as that in Theorem 4.1. Moreover, the maximum solution to the problem  ) is also a solution to the problem
) is also a solution to the problem  .
.
Since  , from the variational characterization of the metric projection, it yields that all solutions to the problem
, from the variational characterization of the metric projection, it yields that all solutions to the problem  must be contained in
must be contained in  . Hence, the maximum solution to the problem
. Hence, the maximum solution to the problem  ) in
) in  is the maximum solution to the problem
is the maximum solution to the problem  in
in  . This theorem is proved.
. This theorem is proved.
Next, we consider a special type of mappings which has been used by number of authors in the fields of variational inequality theory and complementarity theory (see [4–6]). Let  be a closed convex
be a closed convex  -sublattice of a Hilbert lattice
-sublattice of a Hilbert lattice  . A set-valued correspondence
. A set-valued correspondence  is said to be a
is said to be a  -completely continuous mapping if
-completely continuous mapping if  is a
is a  -bounded and closed
-bounded and closed  -sublattice of
-sublattice of  . A set-valued correspondence
. A set-valued correspondence  is said to be a
is said to be a  -completely continuous field if
-completely continuous field if  has the representation:
has the representation:  , for some
, for some  -completely continuous mapping
-completely continuous mapping  . With these concepts, we provide an immediate consequence of Theorem 4.2 below.
. With these concepts, we provide an immediate consequence of Theorem 4.2 below.
Corollary 4.3.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a closed convex
a closed convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued
be a set-valued  -completely continuous mapping with the representation
-completely continuous mapping with the representation  , for some
, for some  -completely continuous mapping
-completely continuous mapping  . In addition, if f is upper (lower)
. In addition, if f is upper (lower)  -preserving with upper (lower) bound
-preserving with upper (lower) bound  -closed values at all points in
-closed values at all points in  , then
, then  is solvable and it has a maximum (minimum) solution.
is solvable and it has a maximum (minimum) solution.
Proof.
Taking  in Theorem 4.2, we get
in Theorem 4.2, we get

From the condition of  -completely continuous mapping, it implies that
-completely continuous mapping, it implies that 
 -bounded closed
-bounded closed  -sublattice of
-sublattice of  . So,
. So,  satisfies all conditions of Theorem 4.2. Then, this corollary follows immediately.
satisfies all conditions of Theorem 4.2. Then, this corollary follows immediately.
The solvability of a general variational inequality in Theorem 4.2 can be extended as below. But, the existence of maximum or minimum solution will be failed.
Theorem 4.4.
Let  be a Hilbert lattice and
be a Hilbert lattice and  a closed convex
a closed convex  -sublattice of
-sublattice of  . Let
. Let  be a set-valued correspondence. Suppose that
be a set-valued correspondence. Suppose that  is upper (lower)
is upper (lower)  -preserving with upper (lower) bound
-preserving with upper (lower) bound  -closed values at all points in
-closed values at all points in  , for some function
, for some function  . In addition, if there exists a nonempty, closed, bounded, and convex
. In addition, if there exists a nonempty, closed, bounded, and convex  -sublattice
-sublattice such that
such that  is a nonempty closed bounded and convex
is a nonempty closed bounded and convex  -sublattice in
-sublattice in , then
, then  is solvable.
is solvable.
Proof.
As restricting to the mapping  , the proof of this theorem is very similar to the proof of the solvability in Theorem 4.2. It is omitted.
, the proof of this theorem is very similar to the proof of the solvability in Theorem 4.2. It is omitted.
References
Cottle RW, Pang JS: A least-element theory of solving linear complementarity problems as linear programs. Mathematics of Operations Research 1978,3(2):155–170. 10.1287/moor.3.2.155
Cryer CW, Dempster MAH: Equivalence of linear complementarity problems and linear programs in vector lattice Hilbert spaces. SIAM Journal on Control and Optimization 1980,18(1):76–90. 10.1137/0318005
Cryer CW, Dempster MAH: Equivalence of linear complementarity problems and linear programs in vector lattice Hilbert spaces. SIAM Journal on Control and Optimization 1980,18(1):76–90. 10.1137/0318005
Isac G: Complementarity Problems, Lecture Notes in Mathematics. Volume 1528. Springer, Berlin, UK; 1992:vi+297.
Isac G, Li J: Complementarity problems, Karamardian's condition and a generalization of Harker-Pang condition. Nonlinear Analysis Forum 2001,6(2):383–390.
Isac G, Sehgal VM, Singh SP: An alternate version of a variational inequality. Indian Journal of Mathematics 1999,41(1):25–31.
Nishimura H, Ok EA: Solvability of variational inequalities on Hilbert lattices. to appear
Park S: Generalized equilibrium problems and generalized complementarity problems. Journal of Optimization Theory and Applications 1997,95(2):409–417. 10.1023/A:1022643407038
Topkis DM: Supermodularity and Complementarity, Frontiers of Economic Research. Princeton University Press, Princeton, NJ, USA; 1998:xii+272.
Yao JC, Guo J-S: Variational and generalized variational inequalities with discontinuous mappings. Journal of Mathematical Analysis and Applications 1994,182(2):371–392. 10.1006/jmaa.1994.1092
Zhang CJ: Generalized variational inequalities and generalized quasi-variational inequalities. Applied Mathematics and Mechanics 1993,14(4):315–325.
Zhang C-J: Existence of solutions of two abstract variational inequalities. In Fixed Point Theory and Applications. Vol. 2. Nova Science, Huntington, NY, USA; 2001:153–161.
Borwein JM, Dempster MAH: The linear order complementarity problem. Mathematics of Operations Research 1989,14(3):534–558. 10.1287/moor.14.3.534
Borwein JM, Yost DT: Absolute norms on vector lattices. Proceedings of the Edinburgh Mathematical Society II 1984,27(2):215–222.
Smithson RE: Fixed points of order preserving multifunctions. Proceedings of the American Mathematical Society 1971,28(1):304–310. 10.1090/S0002-9939-1971-0274349-1
Acknowledgment
This research was partially supported by the Grant NSC 99-2115-M-110-004-MY3. The authors are grateful to Professor Nishimura and Professor Ok for their valuable communications and suggestions, which improved the presentation of this paper.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Li, J., Yao, JC. The Existence of Maximum and Minimum Solutions to General Variational Inequalities in the Hilbert Lattices. Fixed Point Theory Appl 2011, 904320 (2011). https://doi.org/10.1155/2011/904320
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/904320
 on
on 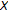 is compatible with the partial order
is compatible with the partial order  , that is,
, that is,