- Research Article
- Open access
- Published:
Asymptotically Pseudocontractions, Banach Operator Pairs and Best Simultaneous Approximations
Fixed Point Theory and Applications volume 2011, Article number: 812813 (2011)
Abstract
The existence of common fixed points is established for the mappings where  is asymptotically
is asymptotically  -pseudo-contraction on a nonempty subset of a Banach space. As applications, the invariant best simultaneous approximation and strong convergence results are proved. Presented results are generalizations of very recent fixed point and approximation theorems of Khan and Akbar (2009), Chen and Li (2007), Pathak and Hussain (2008), and several others.
-pseudo-contraction on a nonempty subset of a Banach space. As applications, the invariant best simultaneous approximation and strong convergence results are proved. Presented results are generalizations of very recent fixed point and approximation theorems of Khan and Akbar (2009), Chen and Li (2007), Pathak and Hussain (2008), and several others.
1. Introduction and Preliminaries
We first review needed definitions. Let  be a subset of a normed space
be a subset of a normed space  . The set
. The set  is called the set of best approximants to
is called the set of best approximants to  out of
out of  , where
, where  . Suppose that
. Suppose that  and
and  are bounded subsets of
are bounded subsets of  . Then, we write
. Then, we write

The number  is called the Chebyshev radius of
is called the Chebyshev radius of  w.r.t.
w.r.t.  , and an element
, and an element  is called a best simultaneous approximation of
is called a best simultaneous approximation of  w.r.t.
w.r.t.  . If
. If  , then
, then  and
and  is the set of all best approximations,
is the set of all best approximations,  , of
, of  from
from  . We also refer the reader to Milman [1], and Vijayraju [2] for further details. We denote by
. We also refer the reader to Milman [1], and Vijayraju [2] for further details. We denote by  and
and  (
( ), the set of positive integers and the closure (weak closure) of a set
), the set of positive integers and the closure (weak closure) of a set  in
in  , respectively. Let
, respectively. Let  be mappings. The set of fixed points of
be mappings. The set of fixed points of  is denoted by
is denoted by  . A point
. A point  is a coincidence point (common fixed point) of
is a coincidence point (common fixed point) of  and
and  if
if  . The pair
. The pair  is called
is called
(1)commuting [3] if  for all
for all  ,
,
(2)compatible (see [3, 4]) if  whenever
whenever  is a sequence such that
is a sequence such that  for some
for some  in
in  ,
,
(3)weakly compatible if they commute at their coincidence points; that is, if  whenever
whenever  ,
,
(4)Banach operator pair, if the set  is
is  -invariant, namely
-invariant, namely  . Obviously, commuting pair
. Obviously, commuting pair  is a Banach operator pair but converse is not true in general, see [5, 6]. If
is a Banach operator pair but converse is not true in general, see [5, 6]. If  is a Banach operator pair, then
is a Banach operator pair, then  need not be a Banach operator pair (see, e.g., [5, 7, 8]). The set
need not be a Banach operator pair (see, e.g., [5, 7, 8]). The set  is called
is called  -starshaped with
-starshaped with  , if the segment
, if the segment  joining
joining  to
to  is contained in
is contained in  for all
for all  . The map
. The map  defined on a
defined on a  -starshaped set
-starshaped set  is called affine if
is called affine if

Suppose that  is
is  -starshaped with
-starshaped with  and is both
and is both  - and
- and  -invariant. Then,
-invariant. Then,  and
and  are called,
are called,
(5) -subweakly commuting on
-subweakly commuting on  (see [9]) if for all
(see [9]) if for all  , there exists a real number
, there exists a real number  such that
such that  ,
,
(6)uniformly -subweakly commuting on
-subweakly commuting on  (see [10]) if there exists a real number
(see [10]) if there exists a real number  such that
such that  , for all
, for all  and
and  . The map
. The map  is said to be demiclosed at 0 if, for every sequence
is said to be demiclosed at 0 if, for every sequence  in
in  converging weakly to
converging weakly to  and
and  converges to
converges to  , then
, then  .
.
The classical Banach contraction principle has numerous generalizations, extensions and applications. While considering Lipschitzian mappings, a natural question arises whether it is possible to weaken contraction assumption a little bit in Banach contraction principle and still obtain the existence of a fixed point. In this direction the work of Edelstein [11], Jungck [3], Park [12–18] and Suzuki [19] is worth to mention.
Schu [20] introduced the concept of asymptotically pseudocontraction and proved the existence and convergence of fixed points for this class of maps (see also [21]). Recently, Chen and Li [5] introduced the class of Banach operator pairs, as a new class of noncommuting maps and it has been further studied by Hussain [6], Ćirić et al. [7], Khan and Akbar [22, 23] and Pathak and Hussain [8]. More recently, Zhou [24] established a demiclosedness principle for a uniformly  -Lipschitzian asymptotically pseudocontraction map and as an application obtained a fixed point result for asymptotically pseudocontraction in the setup of a Hilbert space. In this paper, we are able to join the concepts of uniformly
-Lipschitzian asymptotically pseudocontraction map and as an application obtained a fixed point result for asymptotically pseudocontraction in the setup of a Hilbert space. In this paper, we are able to join the concepts of uniformly  -Lipschitzian, asymptotically
-Lipschitzian, asymptotically  -pseudocontraction and Banach operator pair to get the result of Zhou [24] in the setting of a Banach space. As a consequence, the common fixed point and approximation results of Al-Thagafi [25], Beg et al. [10], Chidume et al. [26], Chen and Li [5], Cho et al. [27], Khan and Akbar [22, 23], Pathak and Hussain [8], Schu [28] and Vijayraju [2] are extended to the class of asymptotically
-pseudocontraction and Banach operator pair to get the result of Zhou [24] in the setting of a Banach space. As a consequence, the common fixed point and approximation results of Al-Thagafi [25], Beg et al. [10], Chidume et al. [26], Chen and Li [5], Cho et al. [27], Khan and Akbar [22, 23], Pathak and Hussain [8], Schu [28] and Vijayraju [2] are extended to the class of asymptotically  -pseudocontraction maps.
-pseudocontraction maps.
2. Main Results
Let  be a real Banach space and
be a real Banach space and  be a subset of
be a subset of  . Let
. Let  be mappings. Then
be mappings. Then  is called
is called
(a)an  -contraction if there exists
-contraction if there exists  such that
such that  for any
for any  ; if
; if  , then
, then  is called
is called  -nonexpansive,
-nonexpansive,
(b)asymptotically -nonexpansive [2] if there exists a sequence
-nonexpansive [2] if there exists a sequence  of real numbers with
of real numbers with  and
and  such that
such that

for all  and for each
and for each  ; if
; if  , then
, then  is called
is called  -asymptotically nonexpansive map,
-asymptotically nonexpansive map,
(c)pseudocontraction if and only if for each  , there exists
, there exists  such that
such that

where  is the normalized duality mapping defined by
is the normalized duality mapping defined by

(d)strongly pseudocontraction if and only if for each  , there exists
, there exists  and
and  such that
such that

(e)asymptotically -pseudocontractive if and only if for each
-pseudocontractive if and only if for each  and
and  , there exists
, there exists  and a constant
and a constant  with
with  such that
such that

If  in (2.5), then
in (2.5), then  is called asymptotically
is called asymptotically -pseudocontractive [20, 24, 27],
-pseudocontractive [20, 24, 27],
(f)uniformly -Lipschitzian if there exists some
-Lipschitzian if there exists some  such that
such that

for all  and for each
and for each  ; if
; if  , then
, then  is called uniformly
is called uniformly -Lipschitzian [20, 24, 29].
-Lipschitzian [20, 24, 29].
The map  is called uniformly asymptotically regular [2, 10] on
is called uniformly asymptotically regular [2, 10] on  , if for each
, if for each  , there exists
, there exists  such that
such that  for all
for all  and all
and all  .
.
The class of asymptotically pseudocontraction contains properly the class of asymptotically nonexpansive mappings and every asymptotically nonexpansive mapping is a uniformly  -Lipschitzian [2, 24]. For further details, we refer to [21, 24, 27, 29, 30].
-Lipschitzian [2, 24]. For further details, we refer to [21, 24, 27, 29, 30].
In 1974, Deimling [30] proved the following fixed point theorem.
Theorem D.
Let  be self-map of a closed convex subset
be self-map of a closed convex subset  of a real Banach space
of a real Banach space  . Assume that
. Assume that  is continuous strongly pseudocontractive mapping. Then,
is continuous strongly pseudocontractive mapping. Then,  has a unique fixed point.
has a unique fixed point.
The following result extends and improves Theorem 3.4 of Beg et al. [10], Theorem 2.10 in [22], Theorems 2.2 of [25] and Theorem 4 in [31].
Theorem 2.1.
Let  be self-maps of a subset
be self-maps of a subset  of a real Banach space
of a real Banach space  . Assume that
. Assume that  is closed (resp., weakly closed) and convex,
is closed (resp., weakly closed) and convex,  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive which is also uniformly asymptotically regular on
-pseudocontractive which is also uniformly asymptotically regular on  . If
. If  is compact (resp.,
is compact (resp.,  is weakly compact and
is weakly compact and  is demiclosed at 0) and
is demiclosed at 0) and  , then
, then  .
.
Proof.
For each  , define a self-map
, define a self-map  on
on  by
by

where  and
and  is a sequence of numbers in
is a sequence of numbers in  such that
such that  and
and  . Since
. Since  and
and  is convex with
is convex with  , it follows that
, it follows that  maps
maps  into
into  . As
. As  is convex and
is convex and  (resp.
(resp.  ), so
), so  ) (resp.
) (resp.  ) for each
) for each  . Since
. Since  is a strongly pseudocontractive on
is a strongly pseudocontractive on  , by Theorem D, for each
, by Theorem D, for each  , there exists
, there exists  such that
such that  . As
. As  is bounded, so
is bounded, so  as
as  . Now,
. Now,

Since for each  ,
,  and
and  , therefore
, therefore  . Thus
. Thus  . Also
. Also  is uniformly asymptotically regular, we have from (2.8)
is uniformly asymptotically regular, we have from (2.8)

as  . Thus
. Thus  as
as  . As
. As  is compact, so there exists a subsequence
is compact, so there exists a subsequence  of
of  such that
such that  as
as  . Since
. Since  is a sequence in
is a sequence in  and
and  , therefore
, therefore  . Moreover,
. Moreover,

Taking the limit as  , we get
, we get  . Thus,
. Thus,  proves the first case.
proves the first case.
Since a weakly closed set is closed, by Theorem D, for each  , there exists
, there exists  such that
such that  . The weak compactness of
. The weak compactness of  implies that there is a subsequence
implies that there is a subsequence  of
of  converging weakly to
converging weakly to  as
as  . Since
. Since  is a sequence in
is a sequence in  and
and  , so
, so  . Moreover, we have,
. Moreover, we have,  as
as  . If
. If  is demiclosed at 0, then
is demiclosed at 0, then  . Thus,
. Thus,  .
.
Remark 2.2.
By comparing Theorem 3.4 of Beg et al. [10] with the first case of Theorem 2.1, their assumptions " is closed and
is closed and  -starshaped,
-starshaped,  ,
,  ,
,  are continuous,
are continuous,  is linear,
is linear,  ,
,  is compact,
is compact,  is asymptotically
is asymptotically  -nonexpansive and
-nonexpansive and  and
and  are uniformly
are uniformly  -subweakly commuting on
-subweakly commuting on  " are replaced with "
" are replaced with " is nonempty set,
is nonempty set,  is closed, convex,
is closed, convex,  ,
,  is compact,
is compact,  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive".
-pseudocontractive".
If  is weakly closed and
is weakly closed and  is weakly continuous, then
is weakly continuous, then  is weakly closed and hence closed, thus we obtain the following.
is weakly closed and hence closed, thus we obtain the following.
Corollary 2.3.
Let  be self-maps of a weakly closed subset
be self-maps of a weakly closed subset  of a Banach space
of a Banach space  . Assume that
. Assume that  is weakly continuous,
is weakly continuous,  is nonempty and convex,
is nonempty and convex,  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive which is also uniformly asymptotically regular on
-pseudocontractive which is also uniformly asymptotically regular on  . If
. If  is compact (resp.
is compact (resp.  is weakly compact and
is weakly compact and  is demiclosed at 0) and
is demiclosed at 0) and  is a Banach operator pair, then
is a Banach operator pair, then  .
.
A mapping  on
on  is called pointwise asymptotically nonexpansive [32, 33] if there exists a sequence
is called pointwise asymptotically nonexpansive [32, 33] if there exists a sequence  of functions such that
of functions such that

for all  and for each
and for each  where
where  pointwise on
pointwise on  .
.
An asymptotically nonexpansive mapping is pointwise asymptotically nonexpansive. A pointwise asymptotically nonexpansive map  defined on a closed bounded convex subset of a uniformly convex Banach space has a fixed point and
defined on a closed bounded convex subset of a uniformly convex Banach space has a fixed point and  is closed and convex [32, 33]. Thus we obtain the following.
is closed and convex [32, 33]. Thus we obtain the following.
Corollary 2.4.
Let  be a pointwise asymptotically nonexpansive self-map of a closed bounded convex subset
be a pointwise asymptotically nonexpansive self-map of a closed bounded convex subset  of a uniformly convex Banach space
of a uniformly convex Banach space  . Assume that
. Assume that  is a self-map of
is a self-map of  which is uniformly
which is uniformly  -Lipschitzian, asymptotically
-Lipschitzian, asymptotically  -pseudocontractive and uniformly asymptotically regular. If
-pseudocontractive and uniformly asymptotically regular. If  is compact (resp.
is compact (resp.  is weakly compact and
is weakly compact and  is demiclosed at 0) and
is demiclosed at 0) and  , then
, then  .
.
Corollary 2.5 (see [24, Theorem 3.3]).
Let  be self-map of a closed bounded and convex subset
be self-map of a closed bounded and convex subset  of a real Hilbert space
of a real Hilbert space  . Assume that
. Assume that  is uniformly Lipschitzian and asymptotically pseudocontractive which is also uniformly asymptotically regular on
is uniformly Lipschitzian and asymptotically pseudocontractive which is also uniformly asymptotically regular on  . Then,
. Then,  .
.
Corollary 2.6.
Let  be a Banach space and
be a Banach space and  and
and  be self-maps of
be self-maps of  . If
. If  ,
,  ,
,  is closed (resp. weakly closed) and convex,
is closed (resp. weakly closed) and convex,  is compact (resp.
is compact (resp.  is weakly compact and
is weakly compact and  is demiclosed at 0),
is demiclosed at 0),  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive which is also uniformly asymptotically regular on
-pseudocontractive which is also uniformly asymptotically regular on  , and
, and  , then
, then  .
.
Remark 2.7.
Corollary 2.6 extends Theorems 4.1 and 4.2 of Chen and Li [5] to a more general class of asymptotically  -pseudocontractions.
-pseudocontractions.
Theorem 2.1 can be extended to uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive map which extends Theorem 2.10 of [22] to asymptotically
-pseudocontractive map which extends Theorem 2.10 of [22] to asymptotically  - pseudocontractions.
- pseudocontractions.
Theorem 2.8.
Let  be self-maps of a subset
be self-maps of a subset  of a Banach space
of a Banach space  . Assume that
. Assume that  is closed (resp. weakly closed) and convex,
is closed (resp. weakly closed) and convex,  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive which is also uniformly asymptotically regular on
-pseudocontractive which is also uniformly asymptotically regular on  . If
. If  is compact (resp.
is compact (resp.  is weakly compact and
is weakly compact and  is demiclosed at 0) and
is demiclosed at 0) and  , then
, then  .
.
Proof.
For each  , define a self-map
, define a self-map  on
on  by
by

where  and
and  is a sequence of numbers in
is a sequence of numbers in  such that
such that  and
and  . Since
. Since  and
and  is convex with
is convex with  , it follows that
, it follows that  maps
maps  into
into  . As
. As  is convex and
is convex and  (resp.
(resp.  ), so
), so  ) (resp.
) (resp.  ) for each
) for each  . Further, since
. Further, since  is a strongly pseudocontractive on
is a strongly pseudocontractive on  , by Theorem D, for each
, by Theorem D, for each  , there exists
, there exists  such that
such that  . Rest of the proof is similar to that of Theorem 2.1.
. Rest of the proof is similar to that of Theorem 2.1.
Corollary 2.9.
Let  be self-maps of a subset
be self-maps of a subset  of a Banach space
of a Banach space  . Assume that
. Assume that  is closed (resp. weakly closed) and convex,
is closed (resp. weakly closed) and convex,  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive which is also uniformly asymptotically regular on
-pseudocontractive which is also uniformly asymptotically regular on  . If
. If  is compact (resp.
is compact (resp.  is weakly compact and
is weakly compact and  is demiclosed at 0) and
is demiclosed at 0) and  and
and  are Banach operator pairs, then
are Banach operator pairs, then  .
.
Corollary 2.10.
Let  be a Banach space and
be a Banach space and  ,
,  , and
, and  be self-maps of
be self-maps of  . If
. If  ,
,  , where
, where  is the set of best simultaneous approximations of
is the set of best simultaneous approximations of  w.r.t
w.r.t  . Assume that
. Assume that  is closed (resp. weakly closed) and convex,
is closed (resp. weakly closed) and convex,  is compact (resp.
is compact (resp.  is weakly compact and
is weakly compact and  is demiclosed at 0),
is demiclosed at 0),  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive which is also uniformly asymptotically regular on
-pseudocontractive which is also uniformly asymptotically regular on  , and
, and  , then
, then  .
.
Remark 2.11.
-
(1)
Theorem 2.2 and 2.7 of Khan and Akbar [23] are particular cases of Corollary 2.10.
-
(2)
By comparing Theorem 2.2 of Khan and Akbar [23] with the first case of Corollary 2.10, their assumptions "
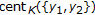 is nonempty, compact, starshaped with respect to an element
is nonempty, compact, starshaped with respect to an element 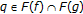 ,
,  is invariant under
is invariant under  ,
, 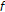 and
and 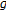 ,
, 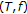 and
and 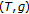 are Banach operator pairs on
are Banach operator pairs on  ,
, 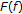 and
and 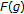 are
are  -starshaped with
-starshaped with 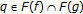 ,
, 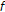 and
and  are continuous and
are continuous and  is asymptotically
is asymptotically 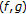 -nonexpansive on
-nonexpansive on 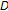 ," are replaced with "
," are replaced with "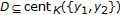 ,
, 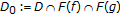 is closed and convex,
is closed and convex,  ,
, 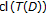 is compact and
is compact and  is uniformly
is uniformly 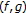 -Lipschitzian and asymptotically
-Lipschitzian and asymptotically 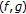 -pseudocontractive on
-pseudocontractive on 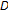 ."
." -
(3)
By comparing Theorem 2.7 of Khan and Akbar [23] with the second case of Corollary 2.10, their assumptions "
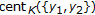 is nonempty, weakly compact, starshaped with respect to an element
is nonempty, weakly compact, starshaped with respect to an element 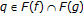 ,
, 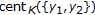 is invariant under
is invariant under  ,
,  and
and 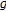 ,
,  and
and  are Banach operator pairs on
are Banach operator pairs on 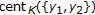 ,
, 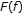 and
and 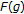 are
are  -starshaped with
-starshaped with 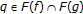 ,
, 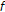 and
and 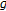 are continuous under weak and strong topologies,
are continuous under weak and strong topologies, 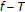 is demiclosed at 0 and
is demiclosed at 0 and  is asymptotically
is asymptotically 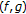 -nonexpansive on
-nonexpansive on 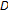 ," are replaced with "
," are replaced with " ,
, 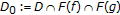 is weakly closed and convex,
is weakly closed and convex, 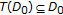 ,
, 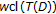 is weakly compact and
is weakly compact and  is demiclosed at 0 and
is demiclosed at 0 and  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically 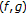 -pseudocontractive on
-pseudocontractive on 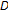 ."
."
We denote by  the class of closed convex subsets of
the class of closed convex subsets of  containing 0. For
containing 0. For  , we define
, we define  =
=  . It is clear that
. It is clear that  (see [9, 25]).
(see [9, 25]).
Theorem 2.12.
Let  be self-maps of a Banach space
be self-maps of a Banach space  . If
. If  and
and  such that
such that  ,
,  is compact (resp.
is compact (resp.  is weakly compact) and
is weakly compact) and  for all
for all  , then
, then  is nonempty, closed and convex with
is nonempty, closed and convex with  . If, in addition,
. If, in addition,  ,
,  is closed (resp. weakly closed) and convex,
is closed (resp. weakly closed) and convex,  is compact (resp.
is compact (resp.  is weakly compact and
is weakly compact and  is demiclosed at 0),
is demiclosed at 0),  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive which is also uniformly asymptotically regular on
-pseudocontractive which is also uniformly asymptotically regular on  , and
, and  , then
, then  .
.
Proof.
We may assume that  . If
. If 
 , then
, then  . Note that
. Note that

Thus,  . If
. If  is compact, then by the continuity of norm, we get
is compact, then by the continuity of norm, we get  for some
for some  .
.
If we assume that  is weakly compact, using Lemma 5.5 in [34, page 192], we can show the existence of a
is weakly compact, using Lemma 5.5 in [34, page 192], we can show the existence of a  such that
such that  .
.
Thus, in both cases, we have

for all  . Hence
. Hence  and so
and so  is nonempty, closed and convex with
is nonempty, closed and convex with  . The compactness of
. The compactness of  (resp. weak compactness of
(resp. weak compactness of  ) implies that
) implies that  is compact (resp.
is compact (resp.  is weakly compact). The result now follows from Theorem 2.8.
is weakly compact). The result now follows from Theorem 2.8.
Remark 2.13.
Theorem 2.12 extends Theorems 4.1 and 4.2 in [25], Theorem 8 in [31], and Theorem 2.15 in [22].
Definition 2.14.
Let  be a nonempty closed subset of a Banach space
be a nonempty closed subset of a Banach space  ,
,  be mappings and
be mappings and  . Then
. Then  and
and  are said to satisfy property
are said to satisfy property  [10, 27] if the following holds: for any bounded sequence
[10, 27] if the following holds: for any bounded sequence  in
in  ,
,  implies
implies  .
.
The normal structure coefficient  of a Banach space
of a Banach space  is defined [10, 26] by
is defined [10, 26] by  , where
, where  is the Chebyshev radius of
is the Chebyshev radius of  relative to itself and
relative to itself and  is diameter of
is diameter of  . The space
. The space  is said to have the uniform normal structure if
is said to have the uniform normal structure if  . A Banach limit
. A Banach limit  is a bounded linear functional on
is a bounded linear functional on  such that
such that  and
and  for all bounded sequences
for all bounded sequences  in
in  . Let
. Let  be bounded sequence in
be bounded sequence in  . Then we can define the real-valued continuous convex function
. Then we can define the real-valued continuous convex function  on
on  by
by  for all
for all  .
.
The following lemmas are well known.
Let  be a Banach space with uniformly Gâteaux differentiable norm and
be a Banach space with uniformly Gâteaux differentiable norm and  . Let
. Let  be bounded sequence in
be bounded sequence in  . Then
. Then  if and only if
if and only if  for all
for all  , where
, where  is the normalized duality mapping and
is the normalized duality mapping and  denotes the generalized duality pairing.
denotes the generalized duality pairing.
Let  be a convex subset of a smooth Banach space
be a convex subset of a smooth Banach space  ,
,  be a nonempty subset of
be a nonempty subset of  and
and  be a retraction from
be a retraction from  onto
onto  . Then
. Then  is sunny and nonexpansive if and only if
is sunny and nonexpansive if and only if  for all
for all  and
and  .
.
Now, we are ready to prove strong convergence to nearest common fixed points of asymptotically  -pseudocontraction mappings.
-pseudocontraction mappings.
Theorem 2.17.
Let  be a subset of a reflexive real Banach space
be a subset of a reflexive real Banach space  with uniformly Gâteaux differentiable norm. Let
with uniformly Gâteaux differentiable norm. Let  and
and  be self-maps on
be self-maps on  such that
such that  is closed and convex,
is closed and convex,  is continuous, uniformly asymptotically regular, uniformly
is continuous, uniformly asymptotically regular, uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive with a sequence
-pseudocontractive with a sequence  . Let
. Let  be sequence of real numbers in
be sequence of real numbers in  such that
such that  and
and  . If
. If  , then we have the following:
, then we have the following:
(A)For each  , there is exactly one
, there is exactly one  in
in  such that
such that

(B)If  is bounded and
is bounded and  and
and  satisfy property
satisfy property  , then
, then  converges strongly to
converges strongly to  , where
, where  is the sunny nonexpansive retraction from
is the sunny nonexpansive retraction from  onto
onto  .
.
Proof.
Part (A) follows from the proof of Theorem 2.1.
-
(B)
As in Theorem 2.1, we get
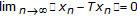 . Since
. Since 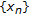 is bounded, we can define a function
is bounded, we can define a function  by
by 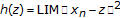 for all
for all  . Since
. Since 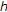 is continuous and convex,
is continuous and convex, 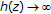 as
as 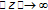 and
and 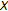 is reflexive,
is reflexive, 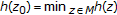 for some
for some  . Clearly, the set
. Clearly, the set  is nonempty. Since
is nonempty. Since 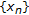 is bounded and
is bounded and  and
and  satisfy property
satisfy property 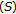 , it follows that
, it follows that  . Suppose that
. Suppose that 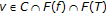 , then by Lemma 2.15, we have
, then by Lemma 2.15, we have 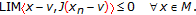 (2.16)
(2.16)
In particular, we have

From (2.8), we have

Now, for any  , we have
, we have

for some  . It follows from (2.18) that
. It follows from (2.18) that

Hence we have

This together with (2.17) implies that  .
.
Thus there is a subsequence  of
of  which converges strongly to
which converges strongly to  . Suppose that there is another subsequence
. Suppose that there is another subsequence  of
of  which converges strongly to
which converges strongly to  (say). Since
(say). Since  is continuous and
is continuous and  ,
,  is a fixed point of
is a fixed point of  . It follows from (2.21) that
. It follows from (2.21) that

Adding these two inequalities, we get

Consequently,  converges strongly to
converges strongly to  . We can define now a mapping
. We can define now a mapping  from
from  onto
onto  by
by  . From (2.21), we have
. From (2.21), we have  for all
for all  and
and  . Thus by Lemma 2.16,
. Thus by Lemma 2.16,  is the sunny nonexpansive retraction on
is the sunny nonexpansive retraction on  . Notice that
. Notice that  and
and  , so by the same argument as in the proof of Theorem 2.1 we obtain,
, so by the same argument as in the proof of Theorem 2.1 we obtain,  .
.
Remark 2.18.
Theorem 2.17 extends Theorem 1 in [27]. Notice that the conditions of the continuity and linearity of  are not needed in Theorem 3.6 of Beg et al. [10]; moreover, we have obtained the conclusion for more general class of uniformly
are not needed in Theorem 3.6 of Beg et al. [10]; moreover, we have obtained the conclusion for more general class of uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically  -pseudocontractive map
-pseudocontractive map  without any type of commutativity of
without any type of commutativity of  and
and  .
.
Corollary 2.19 (see [26, Theorem 3.1]).
Let  be a closed convex bounded subset of a real Banach space
be a closed convex bounded subset of a real Banach space  with uniformly Gâteaux differentiable norm possessing uniform normal structure. Let
with uniformly Gâteaux differentiable norm possessing uniform normal structure. Let  be an asymptotically nonexpansive mapping with a sequence
be an asymptotically nonexpansive mapping with a sequence  . Let
. Let  be fixed,
be fixed,  be sequence of real numbers in
be sequence of real numbers in  such that
such that  and
and  . Then,
. Then,
(A)for each  , there is unique
, there is unique  in
in  such that
such that

(B)if  , then
, then  converges strongly to a fixed point of
converges strongly to a fixed point of  .
.
Remark 2.20.
-
(1)
Theorem 2.17 improves and extends the results of Beg et al. [10], Cho et al. [27], and Schu [20, 28] to more general class of Banach operators.
-
(2)
It would be interesting to prove similar results in Modular Function Spaces (cf. [29]).
-
(3)
Let
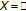 with the usual norm and
with the usual norm and 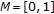 . A mapping
. A mapping  is defined by
is defined by  , for
, for 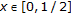 and
and  , for
, for 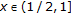 and
and  on
on 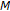 . Clearly,
. Clearly,  is not
is not 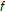 -nonexpansive [21] (e.g.,
-nonexpansive [21] (e.g., 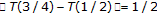 and
and 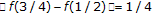 ). But,
). But,  is a
is a 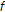 -pseudocontractive mapping.
-pseudocontractive mapping.
References
Milman PD: On best simultaneous approximation in normed linear spaces. Journal of Approximation Theory 1977,20(2):223–238. 10.1016/0021-9045(77)90077-6
Vijayraju P: Applications of fixed point theorem to best simultaneous approximations. Indian Journal of Pure and Applied Mathematics 1993, 21–26.
Jungck G: Common fixed points for commuting and compatible maps on compacta. Proceedings of the American Mathematical Society 1988,103(3):977–983. 10.1090/S0002-9939-1988-0947693-2
Jungck G, Hussain N: Compatible maps and invariant approximations. Journal of Mathematical Analysis and Applications 2007,325(2):1003–1012. 10.1016/j.jmaa.2006.02.058
Chen J, Li Z: Common fixed-points for Banach operator pairs in best approximation. Journal of Mathematical Analysis and Applications 2007,336(2):1466–1475. 10.1016/j.jmaa.2007.01.064
Hussain N: Common fixed points in best approximation for Banach operator pairs with Ćirić type -contractions. Journal of Mathematical Analysis and Applications 2008,338(2):1351–1363. 10.1016/j.jmaa.2007.06.008
Ćirić L, Hussain N, Akbar F, Ume JS: Common fixed points for Banach operator pairs from the set of best approximations. Bulletin of the Belgian Mathematical Society 2009,16(2):319–336.
Pathak HK, Hussain N: Common fixed points for Banach operator pairs with applications. Nonlinear Analysis: Theory, Methods & Applications 2008,69(9):2788–2802. 10.1016/j.na.2007.08.051
Hussain N, Jungck G: Common fixed point and invariant approximation results for noncommuting generalized-nonexpansive maps. Journal of Mathematical Analysis and Applications 2006,321(2):851–861. 10.1016/j.jmaa.2005.08.045
Beg I, Sahu DR, Diwan SD: Approximation of fixed points of uniformly -subweakly commuting mappings. Journal of Mathematical Analysis and Applications 2006,324(2):1105–1114. 10.1016/j.jmaa.2006.01.024
Edelstein M: On fixed and periodic points under contractive mappings. Journal of the London Mathematical Society Second Series 1962, 37: 74–79. 10.1112/jlms/s1-37.1.74
Park S: A generalization of a theorem of Janos and Edelstein. Proceedings of the American Mathematical Society 1977,66(2):344–346. 10.1090/S0002-9939-1977-0454907-7
Park S: Fixed points of -contractive maps. The Rocky Mountain Journal of Mathematics 1978,8(4):743–750. 10.1216/RMJ-1978-8-4-743
Park S: On -nonexpansive maps. Journal of the Korean Mathematical Society 1979–1980,16(1):29–38.
Park S: On general contractive-type conditions. Journal of the Korean Mathematical Society 1980/81,17(1):131–140.
Park S: Some general theorems on common fixed points. Kobe Journal of Mathematics 1988,4(2):141–145.
Park S: Best approximations and fixed points of nonexpansive maps in Hilbert spaces. Numerical Functional Analysis and Optimization. 1997,18(5–6):649–657.
Park S: A unified fixed point theory in generalized convex spaces. Acta Mathematica Sinica, English Series 2007,23(8):1509–1526. 10.1007/s10114-007-0947-3
Suzuki T: A generalized Banach contraction principle that characterizes metric completeness. Proceedings of the American Mathematical Society 2008,136(5):1861–1869.
Schu J: Iterative construction of fixed points of asymptotically nonexpansive mappings. Journal of Mathematical Analysis and Applications 1991,158(2):407–413. 10.1016/0022-247X(91)90245-U
Song Y: Iterative convergence to Cesàro means for continuous pseudocontractive mappings. Nonlinear Analysis: Theory, Methods & Applications 2009,71(7–8):2792–2800. 10.1016/j.na.2009.01.123
Khan AR, Akbar F: Best simultaneous approximations, asymptotically nonexpansive mappings and variational inequalities in Banach spaces. Journal of Mathematical Analysis and Applications 2009,354(2):469–477. 10.1016/j.jmaa.2009.01.007
Khan AR, Akbar F: Common fixed points from best simultaneous approximations. Taiwanese Journal of Mathematics 2009,13(5):1379–1386.
Zhou H: Demiclosedness principle with applications for asymptotically pseudo-contractions in Hilbert spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,70(9):3140–3145. 10.1016/j.na.2008.04.017
Al-Thagafi MA: Common fixed points and best approximation. Journal of Approximation Theory 1996,85(3):318–323. 10.1006/jath.1996.0045
Chidume CE, Li J, Udomene A: Convergence of paths and approximation of fixed points of asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 2005,133(2):473–480. 10.1090/S0002-9939-04-07538-0
Cho YJ, Sahu DR, Jung JS: Approximation of fixed points of asymptotically pseudocontractive mappings in Banach spaces. Southwest Journal of Pure and Applied Mathematics 2003, (2):49–59.
Schu J: Approximation of fixed points of asymptotically nonexpansive mappings. Proceedings of the American Mathematical Society 1991,112(1):143–151. 10.1090/S0002-9939-1991-1039264-7
Khamsi MA, Kozlowski WM: On asymptotic pointwise contractions in modular function spaces. Nonlinear Analysis: Theory, Methods & Applications 2010,73(9):2957–2967. 10.1016/j.na.2010.06.061
Deimling K: Zeros of accretive operators. Manuscripta Mathematica 1974, 13: 365–374. 10.1007/BF01171148
Habiniak L: Fixed point theorems and invariant approximations. Journal of Approximation Theory 1989,56(3):241–244. 10.1016/0021-9045(89)90113-5
Hussain N, Khamsi MA: On asymptotic pointwise contractions in metric spaces. Nonlinear Analysis: Theory, Methods & Applications 2009,71(10):4423–4429. 10.1016/j.na.2009.02.126
Kirk WA, Xu H-K: Asymptotic pointwise contractions. Nonlinear Analysis: Theory, Methods & Applications 2008,69(12):4706–4712. 10.1016/j.na.2007.11.023
Singh S, Watson B, Srivastava P: Fixed Point Theory and Best Approximation: The KKM-Map Principle, Mathematics and Its Applications. Volume 424. Kluwer Academic Publishers, Dordrecht, The Netherlands; 1997:x+220.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Hussain, N. Asymptotically Pseudocontractions, Banach Operator Pairs and Best Simultaneous Approximations. Fixed Point Theory Appl 2011, 812813 (2011). https://doi.org/10.1155/2011/812813
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/812813
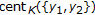 is nonempty, compact, starshaped with respect to an element
is nonempty, compact, starshaped with respect to an element 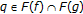 ,
,  is invariant under
is invariant under  ,
, 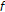 and
and 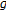 ,
, 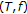 and
and 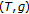 are Banach operator pairs on
are Banach operator pairs on  ,
, 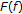 and
and 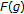 are
are  -starshaped with
-starshaped with 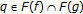 ,
, 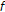 and
and  are continuous and
are continuous and  is asymptotically
is asymptotically 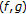 -nonexpansive on
-nonexpansive on 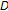 ," are replaced with "
," are replaced with "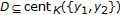 ,
, 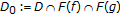 is closed and convex,
is closed and convex,  ,
, 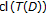 is compact and
is compact and  is uniformly
is uniformly 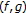 -Lipschitzian and asymptotically
-Lipschitzian and asymptotically 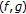 -pseudocontractive on
-pseudocontractive on 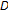 ."
."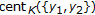 is nonempty, weakly compact, starshaped with respect to an element
is nonempty, weakly compact, starshaped with respect to an element 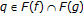 ,
, 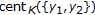 is invariant under
is invariant under  ,
,  and
and 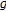 ,
,  and
and  are Banach operator pairs on
are Banach operator pairs on 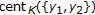 ,
, 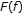 and
and 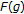 are
are  -starshaped with
-starshaped with 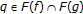 ,
, 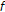 and
and 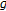 are continuous under weak and strong topologies,
are continuous under weak and strong topologies, 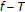 is demiclosed at 0 and
is demiclosed at 0 and  is asymptotically
is asymptotically 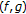 -nonexpansive on
-nonexpansive on 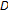 ," are replaced with "
," are replaced with " ,
, 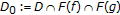 is weakly closed and convex,
is weakly closed and convex, 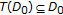 ,
, 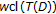 is weakly compact and
is weakly compact and  is demiclosed at 0 and
is demiclosed at 0 and  is uniformly
is uniformly  -Lipschitzian and asymptotically
-Lipschitzian and asymptotically 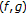 -pseudocontractive on
-pseudocontractive on 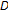 ."
."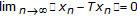 . Since
. Since 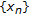 is bounded, we can define a function
is bounded, we can define a function  by
by 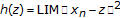 for all
for all  . Since
. Since 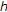 is continuous and convex,
is continuous and convex, 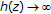 as
as 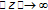 and
and 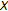 is reflexive,
is reflexive, 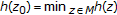 for some
for some  . Clearly, the set
. Clearly, the set  is nonempty. Since
is nonempty. Since 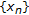 is bounded and
is bounded and  and
and  satisfy property
satisfy property 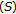 , it follows that
, it follows that  . Suppose that
. Suppose that 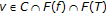 , then by Lemma 2.15, we have
, then by Lemma 2.15, we have 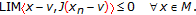
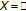 with the usual norm and
with the usual norm and 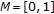 . A mapping
. A mapping  is defined by
is defined by  , for
, for 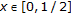 and
and  , for
, for 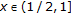 and
and  on
on 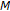 . Clearly,
. Clearly,  is not
is not 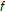 -nonexpansive [
-nonexpansive [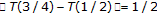 and
and 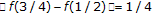 ). But,
). But,  is a
is a 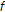 -pseudocontractive mapping.
-pseudocontractive mapping.