- Research Article
- Open access
- Published:
Strong Convergence Theorems of the Ishikawa Process with Errors for Strictly Pseudocontractive Mapping of Browder-Petryshyn Type in Banach Spaces
Fixed Point Theory and Applications volume 2011, Article number: 706206 (2011)
Abstract
We prove several strong convergence theorems for the Ishikawa iterative sequence with errors to a fixed point of strictly pseudocontractive mapping of Browder-Petryshyn type in Banach spaces and give sufficient and necessary conditions for the convergence of the scheme to a fixed point of the mapping. The results presented in this work give an affirmative answer to the open question raised by Zeng et al. 2006, and generalize the corresponding result of Zeng et al. 2006, Osilike and Udomene 2001, and others.
1. Introduction and Preliminaries
Let  be a real Banach space and
be a real Banach space and  its dual.
its dual.  denotes the generalized duality pairing between
denotes the generalized duality pairing between  and
and  . Let
. Let  be the normalized duality mapping defined by the following:
be the normalized duality mapping defined by the following:

It is well known that if  is smooth, then
is smooth, then  is single-valued. In this paper, we denote a single-valued selection of the normalized duality mapping by
is single-valued. In this paper, we denote a single-valued selection of the normalized duality mapping by  .
.  denotes the identity operator.
denotes the identity operator.  is the fixed point set of
is the fixed point set of  , that is,
, that is,  .
.
Definition 1.1 (see [1]).
A mapping  is said to be strictly pseudocontractive if there exists
is said to be strictly pseudocontractive if there exists  and
and  , such that
, such that

Remark 1.2.
-
(i)
Without loss of generality, we may assume
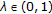 . Inequality (1.2) can be written in the form
. Inequality (1.2) can be written in the form  (1.3)
(1.3)
-
(ii)
If
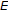 is a Hilbert space, then inequality (1.2) is equivalent to the following inequality:
is a Hilbert space, then inequality (1.2) is equivalent to the following inequality:  (1.4)
(1.4)
-
(iii)
 is a Lipschitz continuous mapping, that is,
is a Lipschitz continuous mapping, that is, 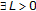 , s.t,
, s.t, 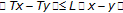 . In fact, by (1.3), we have
. In fact, by (1.3), we have 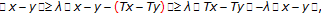 (1.5)
(1.5)
so that,

where  .
.
Definition 1.3.
A mapping  is said to be
is said to be
(i)compact, if for any bounded sequence  in
in  , there exists a strongly convergent subsequence of
, there exists a strongly convergent subsequence of  , or
, or
(ii)demicompact, if for any bounded sequence  in
in  , whenever
, whenever  is strongly convergent, there exists a strongly convergent subsequence of
is strongly convergent, there exists a strongly convergent subsequence of  .
.
Let us recall some important iterative processes.
Definition 1.4 (Ishikawa iterative process with errors in the sense of Liu [2]).
Let  be a nonempty convex subset of
be a nonempty convex subset of  with
with  . For any
. For any  , the sequence
, the sequence  is defined as follows:
is defined as follows:

where  and
and  are appropriate sequences in
are appropriate sequences in  , and
, and  ,
,  , are appropriate sequences in
, are appropriate sequences in  .
.
If  for all
for all  , then (1.7) reduces to Mann iterative process with errors as follows:
, then (1.7) reduces to Mann iterative process with errors as follows:

Definition 1.5 (Ishikawa iterative process with errors in the sense of Xu [3]).
Let  be a nonempty convex subset of
be a nonempty convex subset of  . For any
. For any  , the sequence
, the sequence  is defined as follows:
is defined as follows:

where  and
and  are bounded sequences in
are bounded sequences in  , and
, and  ,
,  ,
,  ,
,  are real sequences in
are real sequences in  satisfying
satisfying  ,
,  , for all
, for all  .
.
If  for all
for all  , then (1.9) reduces to Mann iterative process with errors as follows:
, then (1.9) reduces to Mann iterative process with errors as follows:

Remark 1.6.
-
(i)
If
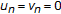 in (1.7) or
in (1.7) or  in (1.9), then (1.7) and (1.9) reduce to Ishikawa iterative process [4],
in (1.9), then (1.7) and (1.9) reduce to Ishikawa iterative process [4], 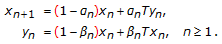 (1.11)
(1.11)
-
(ii)
If
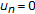 in (1.8) or
in (1.8) or 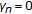 in (1.10), then (1.8) and (1.10) reduce to Mann iterative process [5],
in (1.10), then (1.8) and (1.10) reduce to Mann iterative process [5],  (1.12)
(1.12)
In 1974, Rhoades [6] proved strong convergence theorem by the Mann iterative process to a fixed point of strictly pseudocontractive mapping defined on a nonempty compact convex subset of a Hilbert space. In 2001, Osilike and Udomene [7] proved weak and strong convergence theorems for strictly pseudocontractive mapping in a real  -uniformly smooth Banach space
-uniformly smooth Banach space  which is also uniform convex.
which is also uniform convex.
In 2006, Zeng et al. [8] established the sufficient and necessary conditions on the strong convergence to a fixed point of strictly pseudocontractive mapping in a real  -uniformly smooth Banach space. They got the following main results.
-uniformly smooth Banach space. They got the following main results.
Theorem 1.7.
Let  and
and  be a real
be a real  -uniformly smooth Banach space, let
-uniformly smooth Banach space, let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  with
with  , and let
, and let  be a strictly pseudocontractive mapping with
be a strictly pseudocontractive mapping with  . Let
. Let  be a bounded sequence in
be a bounded sequence in  . Let
. Let  and
and  be real sequences in
be real sequences in  satisfying the following conditions:
satisfying the following conditions:
(i) ;
;
(ii) , and
, and  , where
, where  and
and  is a constant depending on
is a constant depending on  .
.
From an arbitrary  , let
, let  be defined by the following:
be defined by the following:

Then  converges strongly to a fixed point of
converges strongly to a fixed point of  if and only if
if and only if  is bounded and
is bounded and  , where
, where  .
.
In the end of Zeng et al. [8], they raised an open question.
Open Question 1.
Can the Ishikawa iterative process with errors (1.7) be extended to Theorem 1.7?
At the same year, Zeng et al. [9] proved the following strong convergence theorem for strictly pseudocontractive mappings.
Theorem 1.8.
Let  and
and  be a real
be a real  -uniformly smooth Banach space. Let
-uniformly smooth Banach space. Let  be a nonempty closed convex subset of
be a nonempty closed convex subset of  , and let
, and let  be compact or demicompact, and strictly pseudocontractive with
be compact or demicompact, and strictly pseudocontractive with  . Let
. Let  be a bounded sequence in
be a bounded sequence in  . Let
. Let  ,
,  , and
, and  be real sequences in
be real sequences in  satisfying the following conditions:
satisfying the following conditions:
(i) , for all
, for all  ;
;
(ii) ,
,  and
and  ;
;
(iii) and
and  , where
, where  .
.
From an arbitrary  , let
, let  be defined by the following:
be defined by the following:

If  is the bounded sequence, then
is the bounded sequence, then  converges strongly to a fixed point of
converges strongly to a fixed point of  .
.
They raised another open question.
Open Question 2.
Can the Ishikawa iterative process with errors (1.9) be extended to Theorem 1.8?
We have answered the Open Question 1 in [10]. The purpose of this paper is to answer the Open Question 2, and we prove some strong convergence theorems for strictly pseudocontractive mapping in Banach spaces, which improve Theorem 1.8 in the following:
(i) -uniformly smooth Banach spaces can be replaced by general Banach spaces.
-uniformly smooth Banach spaces can be replaced by general Banach spaces.
(ii)Remove the boundedness assumption of  .
.
-
(iii)
Iterative process (1.14) can be replaced by Ishikawa iterative process with errors (1.9).
Respectively, our results improve and generalize the corresponding results of Zeng el al. [8], Osilike and Udomene [7], and others.
In the sequel, we will need the following lemmas.
Lemma 1.9 (see [11]).
Let  ,
,  ,
,  be sequences of nonnegative real numbers satisfying the inequality
be sequences of nonnegative real numbers satisfying the inequality

If  ,
,  , we have (i)
, we have (i)  exists. (ii) In particular, if
exists. (ii) In particular, if  , then
, then  .
.
Lemma 1.10 (see [12]).
Let  be a Banach space and
be a Banach space and  be the normalized duality mapping, then for any
be the normalized duality mapping, then for any  , the following conclusions hold
, the following conclusions hold
(i) , for all
, for all  ;
;
(ii) , for all
, for all  .
.
2. Main Results
In the rest of paper, we denote by  the Lipschitz constant.
the Lipschitz constant.
Lemma 2.1.
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . Let
. Let  be a strictly pseudocontractive mapping with
be a strictly pseudocontractive mapping with  . Let
. Let  ;
;  is defined by (1.9) and satisfying the following conditions:
is defined by (1.9) and satisfying the following conditions:
(i) ;
;
(ii) .
.
Then
(1)there exist two sequences  ,
,  in
in  , such that
, such that  ,
,  , and
, and

Furthermore,  exists.
exists.
(2)For any integer  , there exists a constant
, there exists a constant  , such that
, such that

Proof.
-
(1)
Let
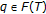 . Since
. Since 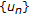 and
and 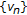 are bounded sequences in
are bounded sequences in 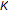 , we have
, we have 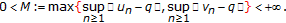 (2.3)
(2.3)
Since  is a strictly pseudocontractive mapping, by Remark 1.2(i),
is a strictly pseudocontractive mapping, by Remark 1.2(i),

By Kato [13], the above inequality is equivalent to

Let  and from (1.9), we have
and from (1.9), we have

It follows that

Observe that

From (2.7) and (2.8), we have

By inequality (2.5), we get

So

Furthermore, set  , then
, then

We make the following estimations.




Substituting (2.14), (2.15), and (2.16) in (2.11), we obtain

where

By conditions (i) and (ii), we have  ,
,  . It follows from Lemma 1.9 that
. It follows from Lemma 1.9 that  exists. This completes the proof of part (1).
exists. This completes the proof of part (1).
-
(2)
If
 , then
, then  . For any integer
. For any integer 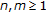 and from part (1), we have
and from part (1), we have  (2.19)
(2.19)
where  . This completes the proof of part (2).
. This completes the proof of part (2).
Lemma 2.2.
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . Let
. Let  be a strictly pseudocontractive mapping with
be a strictly pseudocontractive mapping with  . Let
. Let  be defined as in Lemma 2.1. Then there exists a subsequence
be defined as in Lemma 2.1. Then there exists a subsequence  of
of  , such that
, such that

Proof.
Let  . It follows from (1.3), (1.9), and Lemma 1.10(i) that
. It follows from (1.3), (1.9), and Lemma 1.10(i) that

Let

Then (2.21) becomes

From Lemma 2.1(1),  exists. So
exists. So  is bounded. By inequalities (2.14), (2.15), and (2.16), the sequences
is bounded. By inequalities (2.14), (2.15), and (2.16), the sequences  ,
,  ,
,  are all bounded. Notice the conditions of
are all bounded. Notice the conditions of  and
and  , then
, then  . It follows from (2.23) that
. It follows from (2.23) that

so

Hence,  . Since
. Since  , so we have
, so we have  .
.
By virtue of Lemma 1.10(ii), we obtain

therefore,

Observe the right side of the above inequality, since

and  ,
,  ,
,  are all bounded. Together with
are all bounded. Together with  , then
, then  , that is, there exists a subsequence
, that is, there exists a subsequence  of
of  , such that
, such that

Theorem 2.3.
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . Let
. Let  be a strictly pseudocontractive mapping with
be a strictly pseudocontractive mapping with  . Let
. Let  be defined as in Lemma 2.1, then
be defined as in Lemma 2.1, then  converges strongly to a fixed point of
converges strongly to a fixed point of  if and only if
if and only if  , where
, where  .
.
Proof.
The necessity is obvious. So, we will prove the sufficiency. From Lemma 2.1(1), we have

Therefore,

Note that  ,
,  . By Lemma 1.9 and
. By Lemma 1.9 and  , we get
, we get  .
.
Next, we prove  is a cauchy sequence. For each
is a cauchy sequence. For each  , there exists a natural number
, there exists a natural number  , such that
, such that

where  is the constant in Lemma 2.1 (2). Hence, there exists
is the constant in Lemma 2.1 (2). Hence, there exists  and a natural number
and a natural number  , such that
, such that

From Lemma 2.1(2) and (2.33), for all  , we have
, we have

Hence,  is a cauchy sequence. Since
is a cauchy sequence. Since  is a closed subset of
is a closed subset of  , so
, so  converges strongly to a
converges strongly to a  .
.
Finally, we prove  . In fact, since
. In fact, since  . So, for any
. So, for any  , there exists
, there exists  , such that
, such that  . Then we have
. Then we have

By the arbitrary of  , we know that
, we know that  . Therefore,
. Therefore,  .
.
A mapping  is said to satisfy Condition(A) [14], if there exists a nondecreasing function
is said to satisfy Condition(A) [14], if there exists a nondecreasing function  with
with  ,
,  , for all
, for all  such that
such that  for all
for all  .
.
Theorem 2.4.
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . Let
. Let  be a strictly pseudocontractive mapping with
be a strictly pseudocontractive mapping with  , and satisfy Condition(A). Let
, and satisfy Condition(A). Let  be defined as in Lemma 2.1. Then
be defined as in Lemma 2.1. Then  converges strongly to a fixed point of
converges strongly to a fixed point of  .
.
Proof.
By Lemma 2.2, there exists a subsequence  of
of  , such that
, such that

By Condition(A),  . Since
. Since  is a nondecreasing function and
is a nondecreasing function and  , therefore
, therefore  . The rest of the proof is the same to Theorem 2.3.
. The rest of the proof is the same to Theorem 2.3.
Theorem 2.5.
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . Let
. Let  be a compact and strictly pseudocontractive mapping with
be a compact and strictly pseudocontractive mapping with  . Let
. Let  be defined as in Lemma 2.1. Then
be defined as in Lemma 2.1. Then  converges strongly to a fixed point of
converges strongly to a fixed point of  .
.
Proof.
From Lemma 2.1 (1), it follows that  exists, for any
exists, for any  . By Lemma 2.2, there exists a subsequence
. By Lemma 2.2, there exists a subsequence  of
of  such that
such that  . Since
. Since  is bounded and
is bounded and  is compact,
is compact,  has a strongly convergent subsequence. Without loss of generality, we may assume that
has a strongly convergent subsequence. Without loss of generality, we may assume that  converges strongly to
converges strongly to  . Next, we prove
. Next, we prove  .
.

that is,  . By the Lipschitz continuity of
. By the Lipschitz continuity of  , it follows that
, it follows that

This means that  . By Lemmas 1.9(ii) and 2.1(i), the sequence
. By Lemmas 1.9(ii) and 2.1(i), the sequence  converges strongly to
converges strongly to  .
.
Theorem 2.6.
Let  be a nonempty closed convex subset of a real Banach space
be a nonempty closed convex subset of a real Banach space  . Let
. Let  be a demicompact and strictly pseudocontractive mapping with
be a demicompact and strictly pseudocontractive mapping with  . Let
. Let  be defined as in Lemma 2.1. Then
be defined as in Lemma 2.1. Then  converges strongly to a fixed point of
converges strongly to a fixed point of  .
.
Proof.
From Lemma 2.1(1), it follows that  exists, for any
exists, for any  . By Lemma 2.2, there exists a subsequence
. By Lemma 2.2, there exists a subsequence  of
of  such that
such that  . Since
. Since  is bounded together with
is bounded together with  being demicompact, there exists a subsequence of
being demicompact, there exists a subsequence of  which converges strongly to some
which converges strongly to some  . Taking into account that
. Taking into account that  and the Lipschitz continuity of
and the Lipschitz continuity of  , we have
, we have  . By Lemma 1.9,
. By Lemma 1.9,  converges strongly to
converges strongly to  .
.
References
Browder FE, Petryshyn WV: Construction of fixed points of nonlinear mappings in Hilbert space. Journal of Mathematical Analysis and Applications 1967, 20: 197–228. 10.1016/0022-247X(67)90085-6
Liu LS: Ishikawa and Mann iterative process with errors for nonlinear strongly accretive mappings in Banach spaces. Journal of Mathematical Analysis and Applications 1995,194(1):114–125. 10.1006/jmaa.1995.1289
Xu Y: Ishikawa and Mann iterative processes with errors for nonlinear strongly accretive operator equations. Journal of Mathematical Analysis and Applications 1998,224(1):91–101. 10.1006/jmaa.1998.5987
Ishikawa S: Fixed points by a new iteration method. Proceedings of the American Mathematical Society 1974,44(1):147–150. 10.1090/S0002-9939-1974-0336469-5
Mann WR: Mean value methods in iteration. Proceedings of the American Mathematical Society 1953, 4: 506–510. 10.1090/S0002-9939-1953-0054846-3
Rhoades BE: Fixed point iterations using infinite matrices. Transactions of the American Mathematical Society 1974, 196: 161–176.
Osilike MO, Udomene A: Demiclosedness principle and convergence theorems for strictly pseudocontractive mappings of Browder-Petryshyn type. Journal of Mathematical Analysis and Applications 2001,256(2):431–445. 10.1006/jmaa.2000.7257
Zeng L-C, Wong N-C, Yao J-C: Strong convergence theorems for strictly pseudocontractive mappings of Browder-Petryshyn type. Taiwanese Journal of Mathematics 2006,10(4):837–849.
Zeng LC, Lee GM, Wong NC: Ishikawa iteration with errors for approximating fixed points of strictly pseudocontractive mappings of Browder-Petryshyn type. Taiwanese Journal of Mathematics 2006,10(1):87–99.
Tang YC, Peng JG: On the strong convergence of the Ishikawa process with errors for a strictly pseudocontractive mapping of Browder-Petryshyn type. submitted
Osilike MO, Aniagbosor SC: Weak and strong convergence theorems for fixed points of asymptotically nonexpansive mappings. Mathematical and Computer Modelling 2000,32(10):1181–1191. 10.1016/S0895-7177(00)00199-0
Chang S-S: Some problems and results in the study of nonlinear analysis. Nonlinear Analysis: Theory, Methods & Applications 1997,30(7):4197–4208. 10.1016/S0362-546X(97)00388-X
Kato T: Nonlinear semigroups and evolution equations. Journal of the Mathematical Society of Japan 1964, 19: 508–520.
Senter HF, Dotson WG Jr.: Approximating fixed points of nonexpansive mappings. Proceedings of the American Mathematical Society 1974,44(2):375–380. 10.1090/S0002-9939-1974-0346608-8
Acknowledgments
This work was supported by National Natural Science Foundations of China (60970149) and the Natural Science Foundations of Jiangxi Province (2009GZS0021, 2007GQS2063).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Tang, YC., Cai, Y. & Liu, LW. Strong Convergence Theorems of the Ishikawa Process with Errors for Strictly Pseudocontractive Mapping of Browder-Petryshyn Type in Banach Spaces. Fixed Point Theory Appl 2011, 706206 (2011). https://doi.org/10.1155/2011/706206
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/706206
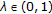 . Inequality (1.2) can be written in the form
. Inequality (1.2) can be written in the form 
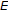 is a Hilbert space, then inequality (1.2) is equivalent to the following inequality:
is a Hilbert space, then inequality (1.2) is equivalent to the following inequality: 
 is a Lipschitz continuous mapping, that is,
is a Lipschitz continuous mapping, that is, 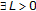 , s.t,
, s.t, 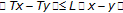 . In fact, by (1.3), we have
. In fact, by (1.3), we have 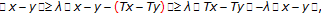
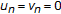 in (1.7) or
in (1.7) or  in (1.9), then (1.7) and (1.9) reduce to Ishikawa iterative process [
in (1.9), then (1.7) and (1.9) reduce to Ishikawa iterative process [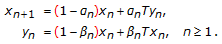
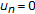 in (1.8) or
in (1.8) or 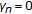 in (1.10), then (1.8) and (1.10) reduce to Mann iterative process [
in (1.10), then (1.8) and (1.10) reduce to Mann iterative process [
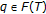 . Since
. Since 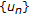 and
and 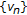 are bounded sequences in
are bounded sequences in 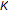 , we have
, we have 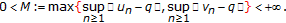
 , then
, then  . For any integer
. For any integer 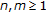 and from part (1), we have
and from part (1), we have 