- Research Article
- Open access
- Published:
Solvability and Algorithms for Functional Equations Originating from Dynamic Programming
Fixed Point Theory and Applications volume 2011, Article number: 701519 (2011)
Abstract
The main purpose of this paper is to study the functional equation arising in dynamic programming of multistage decision processes  ,
,
 . A few iterative algorithms for solving the functional equation are suggested. The existence, uniqueness and iterative approximations of solutions for the functional equation are discussed in the Banach spaces
. A few iterative algorithms for solving the functional equation are suggested. The existence, uniqueness and iterative approximations of solutions for the functional equation are discussed in the Banach spaces  and
and  and the complete metric space
and the complete metric space  , respectively. The properties of solutions, nonnegative solutions, and nonpositive solutions and the convergence of iterative algorithms for the functional equation and other functional equations, which are special cases of the above functional equation, are investigated in the complete metric space
, respectively. The properties of solutions, nonnegative solutions, and nonpositive solutions and the convergence of iterative algorithms for the functional equation and other functional equations, which are special cases of the above functional equation, are investigated in the complete metric space  , respectively. Eight nontrivial examples which dwell upon the importance of the results in this paper are also given.
, respectively. Eight nontrivial examples which dwell upon the importance of the results in this paper are also given.
1. Introduction
The existence, uniqueness, and iterative approximations of solutions for several classes of functional equations arising in dynamic programming were studied by a lot of researchers; see [1–23] and the references therein. Bellman [3], Bhakta and Choudhury [7], Liu [12], Liu and Kang [15], and Liu et al. [18] investigated the following functional equations:

and gave some existence and uniqueness results and iterative approximations of solutions for the functional equations in  . Liu and Kang [14] and Liu and Ume [17] generalized the results in [3, 7, 12, 15, 18] and studied the properties of solutions, nonpositive solutions and nonnegative solutions and the convergence of iterative approximations for the following functional equations, respectively
. Liu and Kang [14] and Liu and Ume [17] generalized the results in [3, 7, 12, 15, 18] and studied the properties of solutions, nonpositive solutions and nonnegative solutions and the convergence of iterative approximations for the following functional equations, respectively

in  .
.
The purpose of this paper is to introduce and study the following functional equations arising in dynamic programming of multistage decision processes:







where  denotes
denotes  or
or  ,
,  and
and  stand for the state and decision vectors, respectively,
stand for the state and decision vectors, respectively,  , and
, and  represent the transformations of the processes, and
represent the transformations of the processes, and  represents the optimal return function with initial
represents the optimal return function with initial  .
.
This paper is divided into four sections. In Section 2, we recall a few basic concepts and notations, establish several lemmas that will be needed further on, and suggest ten iterative algorithms for solving the functional equations (1.3)–(1.9). In Section 3, by applying the Banach fixed-point theorem, we establish the existence, uniqueness, and iterative approximations of solutions for the functional equation (1.3) in the Banach spaces  and
and  , respectively. By means of two iterative algorithms defined in Section 2, we obtain the existence, uniqueness, and iterative approximations of solutions for the functional equation (1.3) in the complete metric space
, respectively. By means of two iterative algorithms defined in Section 2, we obtain the existence, uniqueness, and iterative approximations of solutions for the functional equation (1.3) in the complete metric space  . Under certain conditions, we investigate the behaviors of solutions, nonpositive solutions, and nonnegative solutions and the convergence of iterative algorithms for the functional equations (1.3)–(1.7), respectively, in
. Under certain conditions, we investigate the behaviors of solutions, nonpositive solutions, and nonnegative solutions and the convergence of iterative algorithms for the functional equations (1.3)–(1.7), respectively, in  . In Section 4, we construct eight nontrivial examples to explain our results, which extend and improve substantially the results due to Bellman [3], Bhakta and Choudhury [7], Liu [12], Liu and Kang [14, 15], Liu and Ume [17], Liu et al. [18], and others.
. In Section 4, we construct eight nontrivial examples to explain our results, which extend and improve substantially the results due to Bellman [3], Bhakta and Choudhury [7], Liu [12], Liu and Kang [14, 15], Liu and Ume [17], Liu et al. [18], and others.
2. Lemmas and Algorithms
Throughout this paper, we assume that  ,
,  ,
,  ,
,  denotes the set of positive integers, and, for each
denotes the set of positive integers, and, for each  ,
,  denotes the largest integer not exceeding
denotes the largest integer not exceeding  . Let
. Let  and
and  be real Banach spaces,
be real Banach spaces,  the state space, and
the state space, and  the decision space. Define
the decision space. Define

Clearly  and
and  are Banach spaces with norm
are Banach spaces with norm  .
.
For any  and
and  , let
, let

where  and
and  . It is easy to see that
. It is easy to see that  is a countable family of pseudometrics on
is a countable family of pseudometrics on  . A sequence
. A sequence  in
in  is said to be converge to a point
is said to be converge to a point  if, for any
if, for any 
 as
as  and to be a Cauchy sequence if, for any
and to be a Cauchy sequence if, for any  ,
,  as
as  . It is clear that
. It is clear that  is a complete metric space.
is a complete metric space.
Lemma 2.1.
Let  . Then
. Then
(a) ,
,
(b) for
for  ,
,  ,
,
(c) for
for  ,
,
(d) for
for  ,
,
(e) .
.
Proof.
Clearly (a)–(d) are true. Now we show (e). Note that (e) holds for  . Suppose that (e) is true for some
. Suppose that (e) is true for some  . It follows from (a) and Lemma 2.1 in [17] that
. It follows from (a) and Lemma 2.1 in [17] that

Hence (e) holds for any  . This completes the proof.
. This completes the proof.
Lemma 2.2.
Let  and
and  . Then
. Then
(a) ,
,
(b) .
.
Proof.
It is clear that (a) is true for  . Suppose that (a) is also true for some
. Suppose that (a) is also true for some  . Using Lemma 2.3 in [19] and Lemma 2.1, we infer that
. Using Lemma 2.3 in [19] and Lemma 2.1, we infer that

That is, (a) is true for  . Therefore (a) holds for any
. Therefore (a) holds for any  . Similarly we can prove (b). This completes the proof.
. Similarly we can prove (b). This completes the proof.
Lemma 2.3.
Let  ,
,  be convergent sequences in
be convergent sequences in  . Then
. Then

Proof.
Put  for
for  . In view of Lemma 2.1 we deduce that
. In view of Lemma 2.1 we deduce that

which yields that

This completes the proof.
Lemma 2.4.
-
(a)
Assume that
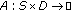 is a mapping such that
is a mapping such that  is bounded for some
is bounded for some 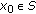 . Then
. Then  (28)
(28)
-
(b)
Assume that
 are mappings such that
are mappings such that 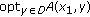 and
and 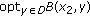 are bounded for some
are bounded for some 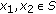 . Then
. Then  (29)
(29)
Proof.
Now we show (a). If  , (a) holds clearly. Suppose that
, (a) holds clearly. Suppose that  . Note that
. Note that

It follows that

which implies that

Next we show (b). If  , (b) is true. Suppose that
, (b) is true. Suppose that  . Note that
. Note that

which yields that

It follows that

which gives that

This completes the proof.
Algorithm 1.
For any  , compute
, compute  by
by

where

Algorithm 2.
For any  , compute
, compute  by (2.17) and (2.18).
by (2.17) and (2.18).
Algorithm 3.
For any  , compute
, compute  by (2.17) and (2.18).
by (2.17) and (2.18).
Algorithm 4.
For any  , compute
, compute  by
by

Algorithm 5.
For any  , compute
, compute  by
by

Algorithm 6.
For any  , compute
, compute  by
by

Algorithm 7.
For any  , compute
, compute  by
by

Algorithm 8.
For any  , compute
, compute  by
by

Algorithm 9.
For any  , compute
, compute  by
by

Algorithm 10.
For any  , compute
, compute  by
by

3. The Properties of Solutions and Convergence of Algorithms
Now we prove the existence, uniqueness, and iterative approximations of solutions for the functional equation (1.3) in  and
and  , respectively, by using the Banach fixed-point theorem.
, respectively, by using the Banach fixed-point theorem.
Theorem 3.1.
Let  be compact. Let
be compact. Let  and
and  satisfy the following conditions:
satisfy the following conditions:
(C1) is bounded in
is bounded in  ;
;
(C2) for some constant
for some constant  ;
;
(C3)for each fixed  ,
,

uniformly for  , respectively.
, respectively.
Then the functional equation (1.3) possesses a unique solution  , and the sequence
, and the sequence  generated by Algorithm 1 converges to
generated by Algorithm 1 converges to  and has the error estimate
and has the error estimate

Proof.
Define a mapping  by
by

Let  and
and  and
and  . It follows from (C1), (C3), and the compactness of
. It follows from (C1), (C3), and the compactness of  that there exist constants
that there exist constants  ,
,  , and
, and  satisfying
satisfying






Using (3.3)–(3.5), (C2), and Lemmas 2.1 and 2.4, we get that

In light of (C2), (3.3), (3.5)–(3.9), and Lemmas 2.1 and 2.4, we deduce that for all  with
with 

Thus (3.10), (3.11), and (2.17) ensure that the mapping  and Algorithm 1 are well defined.
and Algorithm 1 are well defined.
Next we assert that the mapping  is a contraction. Let
is a contraction. Let  ,
,  , and
, and  . Suppose that
. Suppose that  . Choose
. Choose  such that
such that

Lemma 2.1 and (3.12) lead to

which implies that

Letting  in the above inequality, we know that
in the above inequality, we know that

Similarly we conclude that (3.15) holds for  . The Banach fixed-point theorem yields that the contraction mapping
. The Banach fixed-point theorem yields that the contraction mapping  has a unique fixed point
has a unique fixed point  . It is easy to verify that
. It is easy to verify that  is also a unique solution of the functional equation (1.3) in
is also a unique solution of the functional equation (1.3) in  . By means of (2.17), (2.18), (3.15), and
. By means of (2.17), (2.18), (3.15), and

we infer that

which yields that

and the sequence  converges to
converges to  by (2.18). This completes the proof.
by (2.18). This completes the proof.
Dropping the compactness of  and (C3) in Theorem 3.1, we conclude immediately the following result.
and (C3) in Theorem 3.1, we conclude immediately the following result.
Theorem 3.2.
Let  and
and  satisfy conditions (C1) and (C2). Then the functional equation (1.3) possesses a unique solution
satisfy conditions (C1) and (C2). Then the functional equation (1.3) possesses a unique solution  and the sequence
and the sequence  generated by Algorithm 2 converges to
generated by Algorithm 2 converges to  and satisfies (3.2).
and satisfies (3.2).
Next we prove the existence, uniqueness, and iterative approximations of solution for the functional equation (1.3) in  .
.
Theorem 3.3.
Let  and
and  satisfy condition (C2) and the following two conditions:
satisfy condition (C2) and the following two conditions:
(C4) is bounded on
is bounded on  for each
for each  ;
;
(C5) for all
for all  .
.
Then the functional equation (1.3) possesses a unique solution  , and the sequences
, and the sequences  and
and  generated by Algorithms 3 and 4, respectively, converge to
generated by Algorithms 3 and 4, respectively, converge to  and have the error estimates
and have the error estimates

Proof.
Define a mapping  by (3.3). Let
by (3.3). Let  and
and  . Thus (C4) and (C5) guarantee that there exist
. Thus (C4) and (C5) guarantee that there exist  and
and  satisfying
satisfying

Using (3.3), (3.20), (C2), (C5), and Lemmas 2.1 and 2.4, we infer that

which means that  is a self-mapping in
is a self-mapping in  . Consequently, Algorithms 3 and 4 are well defined.
. Consequently, Algorithms 3 and 4 are well defined.
Now we claim that

Let  ,
,  ,
,  , and
, and  . Suppose that
. Suppose that  . Select
. Select  such that (3.12) holds. Thus (3.3), (3.12), (C2), (C5), and Lemma 2.1 ensure that
such that (3.12) holds. Thus (3.3), (3.12), (C2), (C5), and Lemma 2.1 ensure that

which implies that

Similarly we conclude that (3.24) holds for  . As
. As  in (3.24), we get that (3.22) holds.
in (3.24), we get that (3.22) holds.
Let  . It follows from Algorithm 4 that
. It follows from Algorithm 4 that

and (3.22) leads to

which yields that  is a Cauchy sequence in the complete metric space
is a Cauchy sequence in the complete metric space  , and hence
, and hence  converges to some
converges to some  . In light of (3.22) and (C2), we know that
. In light of (3.22) and (C2), we know that

That is, the mapping  is nonexpansive. It follows from (3.27) and Algorithm 4 that
is nonexpansive. It follows from (3.27) and Algorithm 4 that

that is,  . Suppose that there exists
. Suppose that there exists  with
with  . Consequently there exists some
. Consequently there exists some  satisfying
satisfying  . It follows from (3.22) and (C2) that
. It follows from (3.22) and (C2) that

which is a contradiction. Hence the mapping  has a unique fixed point
has a unique fixed point  , which is a unique solution of the functional equation (1.3) in
, which is a unique solution of the functional equation (1.3) in  . Letting
. Letting  in (3.26), we infer that
in (3.26), we infer that

It follows from Algorithm 3, (2.18), and (3.22) that

which gives that  as
as  . This completes the proof.
. This completes the proof.
Next we investigate the behaviors of solutions for the functional equations (1.3)–(1.5) and discuss the convergence of Algorithms 4–6 in  , respectively.
, respectively.
Theorem 3.4.
Let  ,
,  and
and  satisfy the following conditions:
satisfy the following conditions:
(C6) for all
for all  ;
;
(C7) for all
for all  ;
;
(C8) .
.
Then the functional equation (1.3) possesses a solution  satisfying conditions (C9)–(C12) below:
satisfying conditions (C9)–(C12) below:
(C9)the sequence  generated by Algorithm 4 converges to
generated by Algorithm 4 converges to  , where
, where  with
with  for all
for all  ;
;
(C10) for all
for all  ;
;
(C11) for any
for any  ,
,  and
and  ,
,  ,
,  for all
for all  ;
;
(C12) is unique relative to condition (C11).
is unique relative to condition (C11).
Proof.
First of all we assert that

Suppose that there exists some  with
with  . It follows from
. It follows from  that
that

That is,

which is impossible. That is, (3.32) holds. Let the mapping  be defined by (3.3) in
be defined by (3.3) in  . Note that (C6) and (C7) imply (C4) and (C5) by (3.32) and
. Note that (C6) and (C7) imply (C4) and (C5) by (3.32) and  , respectively. As in the proof of Theorem 3.3, by (C8) we conclude that the mapping
, respectively. As in the proof of Theorem 3.3, by (C8) we conclude that the mapping  maps
maps  into
into  and satisfies
and satisfies


That is, the mapping  is nonexpansive.
is nonexpansive.
Let the sequence  be generated by Algorithm 4 and
be generated by Algorithm 4 and  with
with  for all
for all  . We now claim that for each
. We now claim that for each 

Clearly (3.37) holds for  . Assume that (3.37) is true for some
. Assume that (3.37) is true for some  . It follows from (C6)–(C8), (3.32), Algorithm 4, and Lemmas 2.1 and 2.4 that
. It follows from (C6)–(C8), (3.32), Algorithm 4, and Lemmas 2.1 and 2.4 that

That is, (3.37) is true for  . Hence (3.37) holds for each
. Hence (3.37) holds for each  .
.
Next we claim that  is a Cauchy sequence in
is a Cauchy sequence in  . Let
. Let  ,
,  , and
, and  . Suppose that
. Suppose that  . Choose
. Choose  with
with

It follows from (3.39), (C8), and Lemmas 2.2 and 2.3 that

Therefore there exist  and
and  satisfying
satisfying

In a similar method, we can derive that (3.41) holds also for  . Proceeding in this way, we choose
. Proceeding in this way, we choose  and
and  for
for  such that
such that

On account of  , (C7), (3.37), (3.41), and (3.42), we gain that
, (C7), (3.37), (3.41), and (3.42), we gain that

which yields that

Letting  in the above inequality, we infer that
in the above inequality, we infer that

It follows from  and (3.45) that
and (3.45) that  is a Cauchy sequence in
is a Cauchy sequence in  and it converges to some
and it converges to some  . Algorithm 4 and (3.36) lead to
. Algorithm 4 and (3.36) lead to

which yields that  . That is, the functional equation (1.3) possesses a solution
. That is, the functional equation (1.3) possesses a solution  .
.
Now we show (C10). Let  . Put
. Put  . It follows from (3.37), (C7), and
. It follows from (3.37), (C7), and  that
that

that is, (C10) holds.
Next we prove (C11). Given  ,
,  , and
, and  ,
,  ,
,  for
for  . Put
. Put  . Note that (C7) implies that
. Note that (C7) implies that

In view of (3.32), (3.37), (3.48), and  , we know that
, we know that

which means that  .
.
Finally we prove (C12). Assume that the functional equation (1.3) has another solution  that satisfies (C11). Let
that satisfies (C11). Let  and
and  . Suppose that
. Suppose that  . Select
. Select  with
with

On account of (3.50), (C8), and Lemma 2.1, we conclude that there exist  and
and  ,
,  satisfying
satisfying

that is,

Similarly we can prove that (3.52) holds for  . Proceeding in this way, we select
. Proceeding in this way, we select  and
and  for
for  and
and  such that
such that

It follows from (3.52) and (3.53) that

Since  is arbitrary, we conclude immediately that
is arbitrary, we conclude immediately that  . This completes the proof.
. This completes the proof.
Theorem 3.5.
Let  ,
,  and
and  satisfy conditions (C6)–(C8). Then the functional equation (1.4) possesses a solution
satisfy conditions (C6)–(C8). Then the functional equation (1.4) possesses a solution  satisfying conditions (C10)–(C12) and the following two conditions:
satisfying conditions (C10)–(C12) and the following two conditions:
(C13) the sequence  generated by Algorithm 5 converges to
generated by Algorithm 5 converges to  , where
, where  with
with  for all
for all  ;
;
(C14) if  , and
, and  are nonnegative and there exists a constant
are nonnegative and there exists a constant  such that
such that

then  is nonnegative.
is nonnegative.
Proof.
It follows from Theorem 3.4 that the functional equation (1.4) has a solution  that satisfies (C10)–(C13). Now we show (C14). Given
that satisfies (C10)–(C13). Now we show (C14). Given  ,
,  and
and  . It follows from Lemma 2.2, (3.55), and (1.4) that there exist
. It follows from Lemma 2.2, (3.55), and (1.4) that there exist  and
and  such that
such that

That is,

Proceeding in this way, we choose  and
and  for
for  and
and  such that
such that

It follows from (3.57) and (3.58) that

In terms of (C8), (C11), and (3.55), we see that  as
as  . Letting
. Letting  in (3.59), we get that
in (3.59), we get that  . Since
. Since  is arbitrary, we infer immediately that
is arbitrary, we infer immediately that  . This completes the proof.
. This completes the proof.
Theorem 3.6.
Let  ,
,  and
and  satisfy conditions (C6), (C7), and the following condition:
satisfy conditions (C6), (C7), and the following condition:
(C15) , and
, and  are nonnegative and
are nonnegative and  .
.
Then the functional equation (1.6) possesses a solution  satisfying
satisfying 
 for any
for any  , where the sequence
, where the sequence  is generated by Algorithm 7 with
is generated by Algorithm 7 with  , and
, and  for all
for all  .
.
Proof.
We are going to prove that, for any  ,
,

Using  and Algorithm 7, we gain that
and Algorithm 7, we gain that

that is, (3.60) holds for  . Assume that (3.60) holds for some
. Assume that (3.60) holds for some  . Lemma 2.1 and (C15) lead to
. Lemma 2.1 and (C15) lead to

which implies that

and hence (3.60) holds for  . That is, (3.60) holds for any
. That is, (3.60) holds for any  .
.
Now we claim that, for any  ,
,

In fact, (C6) ensures that

that is, (3.64) is true for  . Assume that (3.64) is true for some
. Assume that (3.64) is true for some  . In view of Lemmas 2.1 and 2.4, Algorithm 7, (C6), (C7), and C(15), we gain that
. In view of Lemmas 2.1 and 2.4, Algorithm 7, (C6), (C7), and C(15), we gain that

which yields that (3.64) is true for  . Therefore (3.64) holds for each
. Therefore (3.64) holds for each  . Given
. Given  , note that
, note that  exists. It follows that there exist constants
exists. It follows that there exist constants  and
and  satisfying
satisfying  for any
for any  . Thus (3.64) leads to
. Thus (3.64) leads to

On account of (3.60), (3.67), and Algorithm 7, we deduce that  is convergent for each
is convergent for each  and
and  . Put
. Put

Obviously (3.67) ensures that  . Notice that
. Notice that

Letting  in the above inequality, by Lemmas 2.1 and 2.3 and the convergence of
in the above inequality, by Lemmas 2.1 and 2.3 and the convergence of  we infer that
we infer that

which yields that

It follows from (3.60), (C15), and Lemma 2.1 that

which implies that

Letting  , we gain that
, we gain that

It follows from (3.71) and (3.74) that  is a solution of the functional equation (1.6). This completes the proof.
is a solution of the functional equation (1.6). This completes the proof.
Following similar arguments as in the proof of Theorems 3.5 and 3.6, we have the following results.
Theorem 3.7.
Let  ,
,  and
and  satisfy conditions (C6)–(C8). Then the functional equation (1.5) possesses a solution
satisfy conditions (C6)–(C8). Then the functional equation (1.5) possesses a solution  satisfying conditions (C10)–(C12) and the two following conditions:
satisfying conditions (C10)–(C12) and the two following conditions:
(C16)the sequence  generated by Algorithm 6 converges to
generated by Algorithm 6 converges to  , where
, where  with
with  for all
for all  ;
;
(C17)if  , and
, and  are nonnegative and there exists a constant
are nonnegative and there exists a constant  such that
such that

then  is nonpositive.
is nonpositive.
Theorem 3.8.
Let  ,
,  and
and  satisfy conditions (C6), (C7), and (C15). Then the functional equation (1.7) possesses a solution
satisfy conditions (C6), (C7), and (C15). Then the functional equation (1.7) possesses a solution  satisfying
satisfying  for any
for any  , where the sequence
, where the sequence  is generated by Algorithm 8 with
is generated by Algorithm 8 with  ,
,  and
and  for all
for all  .
.
4. Applications
In this section we use these results in Section 3 to establish the existence of solutions, nonnegative solutions, and nonpositive solutions and iterative approximations for several functional equations, respectively.
Example 4.1.
Let  ,
,  ,
,  , and
, and  . It follows from Theorem 3.1 that the functional equation
. It follows from Theorem 3.1 that the functional equation

possesses a unique solution  and the sequence
and the sequence  generated by Algorithm 1 converges to
generated by Algorithm 1 converges to  and satisfies (3.2).
and satisfies (3.2).
Example 4.2.
Let  ,
,  ,
,  , and
, and  . It is clear that Theorem 3.2 ensures that the functional equation
. It is clear that Theorem 3.2 ensures that the functional equation

possesses a unique solution  and the sequence
and the sequence  generated by Algorithm 2 converges to
generated by Algorithm 2 converges to  and satisfies (3.2).
and satisfies (3.2).
Remark 4.3.
If  ,
,  for all
for all  , then Theorem 3.3 reduces to a result which generalizes the result in [3, page 149] and Theorem 3.4 in [7]. The following example demonstrates that Theorem 3.3 generalizes properly the corresponding results in [3, 7].
, then Theorem 3.3 reduces to a result which generalizes the result in [3, page 149] and Theorem 3.4 in [7]. The following example demonstrates that Theorem 3.3 generalizes properly the corresponding results in [3, 7].
Example 4.4.
Let  ,
,  , and
, and  . It is easy to verify that Theorem 3.3 guarantees that the functional equation
. It is easy to verify that Theorem 3.3 guarantees that the functional equation

has a unique solution in  . However, the results in [3, page 149] and Theorem 3.4 in [7] are valid for the functional equation (4.3).
. However, the results in [3, page 149] and Theorem 3.4 in [7] are valid for the functional equation (4.3).
Remark 4.5.
-
(1)
If
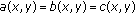 ,
, 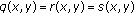 for all
for all 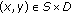 , then Theorems 3.4, 3.5, and 3.7 reduce to three results which generalize and unify the result in [3, page 149], Theorem 3.5 in [7], Theorem 3.5 in [12], Corollaries 2.2 and 2.3 in [14], Corollaries 3.3 and 3.4 in [17], and Theorems 2.3 and 2.4 in [18], respectively.
, then Theorems 3.4, 3.5, and 3.7 reduce to three results which generalize and unify the result in [3, page 149], Theorem 3.5 in [7], Theorem 3.5 in [12], Corollaries 2.2 and 2.3 in [14], Corollaries 3.3 and 3.4 in [17], and Theorems 2.3 and 2.4 in [18], respectively. -
(2)
The results in [3, page 149], Theorem 3.5 in [7], Theorem 3.5 in [12], and Theorem 3.4 in [15] are special cases of Theorem 3.5 with
 ,
, 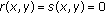 for all
for all 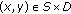 .
.
The examples below show that Theorems 3.4, 3.5, and 3.7 are indeed generalizations of the corresponding results in [3, 7, 12, 14, 15, 17, 18].
Example 4.6.
Let  ,
,  . Define two functions
. Define two functions  by
by  ,
,  for all
for all  . It is easy to see that Theorem 3.4 guarantees that the functional equation
. It is easy to see that Theorem 3.4 guarantees that the functional equation

possesses a solution  that satisfies (C9)–(C12). However, the corresponding results in [3, 7, 12, 14, 17, 18] are not applicable for the functional equation (4.4).
that satisfies (C9)–(C12). However, the corresponding results in [3, 7, 12, 14, 17, 18] are not applicable for the functional equation (4.4).
Example 4.7.
Let  . Put
. Put  ,
,  , and
, and  for all
for all  . It is easy to verify that Theorem 3.5 guarantees that the functional equation
. It is easy to verify that Theorem 3.5 guarantees that the functional equation

has a solution  satisfying (C10)–(C14). But the corresponding results in [3, 7, 12, 14, 15, 17, 18] are not valid for the functional equation (4.5).
satisfying (C10)–(C14). But the corresponding results in [3, 7, 12, 14, 15, 17, 18] are not valid for the functional equation (4.5).
Example 4.8.
Let  ,
,  . Put
. Put  and
and  for all
for all  . It is easy to verify that Theorem 3.6 guarantees that the functional equation
. It is easy to verify that Theorem 3.6 guarantees that the functional equation

has a solution  and the sequence
and the sequence  generated by Algorithm 7 satisfies that
generated by Algorithm 7 satisfies that  for each
for each  , where
, where  with
with

Example 4.9.
Let  . Put
. Put  ,
,  and
and  for all
for all  . It is easy to verify that Theorem 3.7 guarantees that the functional equation
. It is easy to verify that Theorem 3.7 guarantees that the functional equation

has a solution  satisfying (C10)–(C12), (C16), and (C17). But the corresponding results in [3, 7, 12, 14, 17, 18] are not valid for the functional equation (4.8).
satisfying (C10)–(C12), (C16), and (C17). But the corresponding results in [3, 7, 12, 14, 17, 18] are not valid for the functional equation (4.8).
Example 4.10.
Let  ,
,  . Put
. Put  and
and  for all
for all  . It is easy to verify that Theorem 3.8 guarantees that the functional equation
. It is easy to verify that Theorem 3.8 guarantees that the functional equation

possesses a solution  and the sequence
and the sequence  generated by Algorithm 8 satisfies that
generated by Algorithm 8 satisfies that  for each
for each  , where
, where  with
with

References
Belbas SA: Dynamic programming and maximum principle for discrete Goursat systems. Journal of Mathematical Analysis and Applications 1991,161(1):57–77. 10.1016/0022-247X(91)90362-4
Bellman R: Some functional equations in the theory of dynamic programming. I. Functions of points and point transformations. Transactions of the American Mathematical Society 1955, 80: 51–71. 10.1090/S0002-9947-1955-0074692-0
Bellman R: Dynamic Programming. Princeton University Press, Princeton, NJ, USA; 1957:xxv+342.
Bellman R: Methods of Nonlinear Analysis, Vol. II. Academic Press, New York, NY, USA; 1973:xvii+261.
Bellman R, Lee ES: Functional equations in dynamic programming. Aequationes Mathematicae 1978,17(1):1–18. 10.1007/BF01818535
Bellman R, Roosta M: A technique for the reduction of dimensionality in dynamic programming. Journal of Mathematical Analysis and Applications 1982,88(2):543–546. 10.1016/0022-247X(82)90212-8
Bhakta PC, Choudhury SR: Some existence theorems for functional equations arising in dynamic programming. II. Journal of Mathematical Analysis and Applications 1988,131(1):217–231. 10.1016/0022-247X(88)90201-6
Bhakta PC, Mitra S: Some existence theorems for functional equations arising in dynamic programming. Journal of Mathematical Analysis and Applications 1984,98(2):348–346. 10.1016/0022-247X(84)90254-3
Chang S, Ma YH: Coupled fixed points for mixed monotone condensing operators and an existence theorem of the solutions for a class of functional equations arising in dynamic programming. Journal of Mathematical Analysis and Applications 1991,160(2):468–479. 10.1016/0022-247X(91)90319-U
Liu Z: Coincidence theorems for expansion mappings with applications to the solutions of functional equations arising in dynamic programming. Acta Scientiarum Mathematicarum 1999,65(1–2):359–369.
Liu Z: Compatible mappings and fixed points. Acta Scientiarum Mathematicarum 1999,65(1–2):371–383.
Liu Z: Existence theorems of solutions for certain classes of functional equations arising in dynamic programming. Journal of Mathematical Analysis and Applications 2001,262(2):529–553. 10.1006/jmaa.2001.7551
Liu Z, Agarwal RP, Kang SM: On solvability of functional equations and system of functional equations arising in dynamic programming. Journal of Mathematical Analysis and Applications 2004,297(1):111–130. 10.1016/j.jmaa.2004.04.049
Liu Z, Kang SM: Properties of solutions for certain functional equations arising in dynamic programming. Journal of Global Optimization 2006,34(2):273–292. 10.1007/s10898-005-2605-6
Liu Z, Kang SM: Existence and uniqueness of solutions for two classes of functional equations arising in dynamic programming. Acta Mathematicae Applicatae Sinica. English Series 2007,23(2):195–208. 10.1007/s10255-007-0363-6
Liu Z, Kim JK: A common fixed point theorem with applications in dynamic programming. Nonlinear Functional Analysis and Applications 2006,11(1):11–19.
Liu Z, Ume JS: On properties of solutions for a class of functional equations arising in dynamic programming. Journal of Optimization Theory and Applications 2003,117(3):533–551. 10.1023/A:1023945621360
Liu Z, Ume JS, Kang SM: Some existence theorems for functional equations arising in dynamic programming. Journal of the Korean Mathematical Society 2006,43(1):11–28.
Liu Z, Xu Y, Ume JS, Kang SM: Solutions to two functional equations arising in dynamic programming. Journal of Computational and Applied Mathematics 2006,192(2):251–269. 10.1016/j.cam.2005.04.033
Zhang SS: Some existence theorems of common and coincidence solutions for a class of systems of functional equations arising in dynamic programming. Applied Mathematics and Mechanics 1991,12(1):31–37.
Wang C-L: The principle and models of dynamic programming. II. Journal of Mathematical Analysis and Applications 1988,135(1):268–283. 10.1016/0022-247X(88)90153-9
Wang C-L: The principle and models of dynamic programming. III. Journal of Mathematical Analysis and Applications 1988,135(1):284–296. 10.1016/0022-247X(88)90154-0
Wang C-L: The principle and models of dynamic programming. V. Journal of Mathematical Analysis and Applications 1989,137(1):161–167. 10.1016/0022-247X(89)90279-5
Acknowledgments
The authors wish to thank the referees for pointing out some printing errors. This study was supported by research funds from Dong-A University.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Jiang, G., Kang, S. & Kwun, Y. Solvability and Algorithms for Functional Equations Originating from Dynamic Programming. Fixed Point Theory Appl 2011, 701519 (2011). https://doi.org/10.1155/2011/701519
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/701519
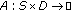 is a mapping such that
is a mapping such that  is bounded for some
is bounded for some 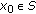 . Then
. Then 
 are mappings such that
are mappings such that 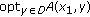 and
and 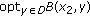 are bounded for some
are bounded for some 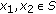 . Then
. Then 
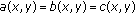 ,
, 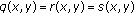 for all
for all 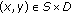 , then Theorems 3.4, 3.5, and 3.7 reduce to three results which generalize and unify the result in [
, then Theorems 3.4, 3.5, and 3.7 reduce to three results which generalize and unify the result in [ ,
, 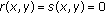 for all
for all 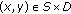 .
.