- Research Article
- Open access
- Published:
Existence of Positive Solutions for Nonlocal Fourth-Order Boundary Value Problem with Variable Parameter
Fixed Point Theory and Applications volume 2011, Article number: 604046 (2011)
Abstract
By using the Krasnoselskii's fixed point theorem and operator spectral theorem, the existence of positive solutions for the nonlocal fourth-order boundary value problem with variable parameter  ,
,  ,
,  ,
,  is considered, where
is considered, where  is a parameter, and
is a parameter, and  ,
,  .
.
1. Introduction
The existence of positive solutions for nonlinear fourth-order multipoint boundary value problems has been studied by many authors using nonlinear alternatives of Leray-Schauder, the fixed point theory, and the method of upper and lower solutions (see, e.g., [1–15] and references therein). The multipoint boundary value problem is in fact a special case of the boundary value problem with integral boundary conditions.
Recently, Bai [16] studied the existence of positive solutions of nonlocal fourth-order boundary value problem

under the assumption:
(A1) and
and  ,
,
(A2) ,
,  ,
,  ,
,  ,
,  ,
,  .
.
In this paper, we study the above generalizing form with variable parameters BVP

where  ,
,  is a parameter.
is a parameter.
Obviously, BVP(1.1) can be regarded as the special case of BVP(1.2) with  . Since the parameters
. Since the parameters  is variable, we cannot expect to transform directly BVP(1.2) into an integral equation as in [16]. We will apply the cone fixed point theory, combining with the operator spectra theorem to establish the existence of positive solutions of BVP(1.2). Our results generalize the main result in [16].
is variable, we cannot expect to transform directly BVP(1.2) into an integral equation as in [16]. We will apply the cone fixed point theory, combining with the operator spectra theorem to establish the existence of positive solutions of BVP(1.2). Our results generalize the main result in [16].
Let  , and we assume that the following conditions hold throughout the paper:
, and we assume that the following conditions hold throughout the paper:
(H1) and
and  ,
,
(H2) ,
,  ,
,  ,
,  and
and  ,
,  .
.
2. The Preliminary Lemmas
Set  ,
,  and
and

By (H1), (H2), we get  ,
,  . Denote by
. Denote by  the Green's function of the problem
the Green's function of the problem

and  the Green's function of the problem
the Green's function of the problem

Then, carefully calculation yield

Lemma 2.1 (see [16]).
Suppose that (A1), (A2) hold. Then, for any  ,
,  solves the problem
solves the problem

if and only if 
Let  , and
, and  , for
, for  .
.  ,
,  ,
,  ,
,  ,
,  .
.
It is easy to show that  are norms on
are norms on  .
.
Lemma 2.2 (see [16]).
 and (
and ( ) is a Banach space.
) is a Banach space.
Lemma 2.3 (see [5]).
Assume that (A1), (A2) hold. Then,
(i) , for
, for  ,
,  ;
;  , for
, for  ,
,  ,
,
(ii) ,
,  for
for  ,
,  ,
,
where  ,
,  ;
;  ,
,  .
.
Denote

Computations yield the following results.
Lemma 2.4 (see [3]).

(i)when  ,
,  ,
,
(ii)when  ,
,  ,
,
(iii)when  ,
,  .
.
Lemma 2.5 (see [16]).
Suppose that (A1), (A2) hold and  ,
,  ,
,  are given as above. Then,
are given as above. Then,
(i) ,
,
(ii) ,
,  .
.
By Lemmas 2.4 and 2.5,  .
.
Take  , by Lemma 2.5,
, by Lemma 2.5,  .
.
Define

Lemma 2.6.
 is completely continuous, and
is completely continuous, and  .
.
Proof.
It is similar to Lemma 6 of [3], so we omit it.
Lemma 2.7 (see [17]).
Let E be a Banach space,  a cone, and
a cone, and  ,
,  be two bounded open sets of
be two bounded open sets of  with
with  . Suppose that
. Suppose that  is a completely continuous operator such that either
is a completely continuous operator such that either
(i) and
and  ,
,  , or
, or
(ii) and
and  ,
, 
holds. Then,  has a fixed point in
has a fixed point in  .
.
3. The Main Results
Suppose that  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  , are defined as in Section 2, we introduce some notations as follows:
, are defined as in Section 2, we introduce some notations as follows:

Theorem 3.1.
Assume that (H1), (H2) hold and  . Then BVP(1.2) has at least one positive solution if one of the following cases holds:
. Then BVP(1.2) has at least one positive solution if one of the following cases holds:
(i) ,
,  ,
,
(ii) ,
,  .
.
Proof.
For any  , consider the following BVP:
, consider the following BVP:

It is easy to see that the above question is equivalent to the following question:

For any  , let
, let  . Obviously, the operator
. Obviously, the operator  is linear. By Lemma 2.2, for all
is linear. By Lemma 2.2, for all  ,
,  ,
,  . Hence
. Hence  , and so
, and so  . On the other hand,
. On the other hand,  is a solution of (3.3) if and only if
is a solution of (3.3) if and only if  satisfies
satisfies  , that is,
, that is,

Owing to  and
and  , the operator
, the operator  maps
maps  into
into  . From
. From  (by Lemma 2.6) together with
(by Lemma 2.6) together with  and condition
and condition  , applying operator spectral theorem, we have that the
, applying operator spectral theorem, we have that the  exists and is bounded. Let
exists and is bounded. Let  , then (3.4) is equivalent to
, then (3.4) is equivalent to  . By the Neumann expansion formula,
. By the Neumann expansion formula,  can be expressed by
can be expressed by

The complete continuity of  with the continuity of
with the continuity of  yields that the operator
yields that the operator  is completely continuous. For all
is completely continuous. For all  , let
, let  , then
, then  , and
, and  . So, we have
. So, we have ,
,  . Hence,
. Hence,

and so  ,
,  .
.
Assume that for all  ,
,  ,
,  , let
, let  , by (3.6) we have
, by (3.6) we have  , and so
, and so  ,
,  . Thus by induction, it follows that
. Thus by induction, it follows that , for all
, for all  ,
,  ,
,  . By (3.5), for all
. By (3.5), for all  , we have
, we have

and so  .
.
On the other hand, for all  , we have
, we have



For any  , define
, define  . By (H1) and (H2), we have that
. By (H1) and (H2), we have that  is continuous. It is easy to see that
is continuous. It is easy to see that  being a positive solution of BVP(1.2) is equivalent to
being a positive solution of BVP(1.2) is equivalent to  being a nonzero solution equation as follows:
being a nonzero solution equation as follows:

Let  . Obviously,
. Obviously,  is completely continuous. We next show that the operator
is completely continuous. We next show that the operator  has a nonzero fixed point in
has a nonzero fixed point in  . Let
. Let

It is easy to know that  is a cone in
is a cone in  ,
,  . Now, we show
. Now, we show  .
.
For  , by (2.7), there is
, by (2.7), there is  ,
, . Hence, by (3.7),
. Hence, by (3.7),  ,
, ,
, . By proof of Lemma 2.5 in [16],
. By proof of Lemma 2.5 in [16],

By (3.7) and (3.10),

Thus  .
.
-
(i)
Since
 , by the definition of
, by the definition of 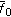 , there exists
, there exists 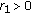 such that
such that  (3.15)
(3.15)
Let  , one has
, one has

So, by (3.10), we get

Hence, for  ,
,

On the other hand, since  , there exists
, there exists  such that
such that

Choose  , let
, let  . For
. For  ,
, , there is
, there is  . Thus,
. Thus,

Hence, for  ,
,

By the use of the Krasnoselskii's fixed point theorem, we know there exists  such that
such that  , namely,
, namely,  is a solution of (1.2) and satisfied
is a solution of (1.2) and satisfied  ,
,  ,
,  .
.
-
(ii)
The proof is similar to (i), so we omit it.
Corollary 3.2.
Assume that (H1), (H2) hold, and  . Then that (1.2) has at least two positive solution, if
. Then that (1.2) has at least two positive solution, if  satisfy
satisfy
(i) ,
,  ,
,
(ii)There exists  such that
such that  , for
, for  ,
,  .
.
Proof.
By the proof of Theorem 3.1, we know that (1) from the condition  , there exists
, there exists  , such that
, such that  ,
,  , (2) from the condition
, (2) from the condition  , there exists
, there exists  ,
,  , such that
, such that  ,
,  , (3) from the condition (ii), there exists
, (3) from the condition (ii), there exists  ,
,  , such that
, such that  ,
,  . By the use of Krasnoselskii's fixed point theorem, it is easy to know that (1.2) has at least two positive solutions.
. By the use of Krasnoselskii's fixed point theorem, it is easy to know that (1.2) has at least two positive solutions.
Corollary 3.3.
Assume (H1), (H2) hold, and  . Then problem (1.2) has at least two positive solution, if
. Then problem (1.2) has at least two positive solution, if  satisfy
satisfy
(i) ,
,  ,
,
(ii)There exists  such that
such that  , for
, for  ,
,  .
.
Proof.
The proof is similar to Corollary 3.2, so we omit it.
Example 3.4.
Consider the following boundary value problem

In this problem, we know that  ,
, ,
, ,
,  , then we can get
, then we can get  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  . Further more, we obtain
. Further more, we obtain  ,
,  , then
, then  ,
,  , so
, so

Thus,  ,
, ,
, , and
, and  satisfy the conditions of Theorem 3.1, and there exists at least a positive solution of the above problem.
satisfy the conditions of Theorem 3.1, and there exists at least a positive solution of the above problem.
References
Bai Z: The method of lower and upper solutions for a bending of an elastic beam equation. Journal of Mathematical Analysis and Applications 2000,248(1):195–202. 10.1006/jmaa.2000.6887
Bai Z: The upper and lower solution method for some fourth-order boundary value problems. Nonlinear Analysis. Theory, Methods & Applications 2007,67(6):1704–1709. 10.1016/j.na.2006.08.009
Chai G: Existence of positive solutions for fourth-order boundary value problem with variable parameters. Nonlinear Analysis. Theory, Methods & Applications 2007,66(4):870–880. 10.1016/j.na.2005.12.028
Feng H, Ji D, Ge W: Existence and uniqueness of solutions for a fourth-order boundary value problem. Nonlinear Analysis. Theory, Methods & Applications 2009,70(10):3561–3566. 10.1016/j.na.2008.07.013
Li Y: Positive solutions of fourth-order boundary value problems with two parameters. Journal of Mathematical Analysis and Applications 2003,281(2):477–484. 10.1016/S0022-247X(03)00131-8
Li Y: Positive solutions of fourth-order periodic boundary value problems. Nonlinear Analysis. Theory, Methods & Applications 2003,54(6):1069–1078. 10.1016/S0362-546X(03)00127-5
Liu X-L, Li W-T: Existence and multiplicity of solutions for fourth-order boundary value problems with three parameters. Mathematical and Computer Modelling 2007,46(3–4):525–534. 10.1016/j.mcm.2006.11.018
Ma H: Symmetric positive solutions for nonlocal boundary value problems of fourth order. Nonlinear Analysis. Theory, Methods & Applications 2008,68(3):645–651. 10.1016/j.na.2006.11.026
Ma R: Existence of positive solutions of a fourth-order boundary value problem. Applied Mathematics and Computation 2005,168(2):1219–1231. 10.1016/j.amc.2004.10.014
Pang C, Dong W, Wei Z: Multiple solutions for fourth-order boundary value problem. Journal of Mathematical Analysis and Applications 2006,314(2):464–476. 10.1016/j.jmaa.2005.04.008
Wei Z, Pang C: Positive solutions and multiplicity of fourth-order m-point boundary value problems with two parameters. Nonlinear Analysis. Theory, Methods & Applications 2007,67(5):1586–1598. 10.1016/j.na.2006.08.001
Yang Y, Zhang J: Existence of solutions for some fourth-order boundary value problems with parameters. Nonlinear Analysis. Theory, Methods & Applications 2008,69(4):1364–1375. 10.1016/j.na.2007.06.035
Yao QL, Bai ZB: Existence of positive solutions of a BVP for . Chinese Annals of Mathematics. Series A 1999,20(5):575–578.
Yao Q: Local existence of multiple positive solutions to a singular cantilever beam equation. Journal of Mathematical Analysis and Applications 2010,363(1):138–154. 10.1016/j.jmaa.2009.07.043
Zhao J, Ge W: Positive solutions for a higher-order four-point boundary value problem with a p-Laplacian. Computers & Mathematics with Applications 2009,58(6):1103–1112. 10.1016/j.camwa.2009.04.022
Bai Z: Positive solutions of some nonlocal fourth-order boundary value problem. Applied Mathematics and Computation 2010,215(12):4191–4197. 10.1016/j.amc.2009.12.040
Guo DJ, Lakshmikantham V: Nonlinear Problems in Abstract Cones, Notes and Reports in Mathematics in Science and Engineering. Volume 5. Academic Press, Boston, Mass, USA; 1988:viii+275.
Acknowledgments
This work is sponsored by the NSFC (no. 11061030), NSFC (no. 11026060), and nwnu-kjcxgc-03-69, 03-61.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Han, X., Gao, H. & Xu, J. Existence of Positive Solutions for Nonlocal Fourth-Order Boundary Value Problem with Variable Parameter. Fixed Point Theory Appl 2011, 604046 (2011). https://doi.org/10.1155/2011/604046
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/604046
 , by the definition of
, by the definition of 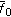 , there exists
, there exists 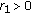 such that
such that 