- Research Article
- Open access
- Published:
On Approximate 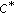 -Ternary
-Ternary 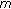 -Homomorphisms: A Fixed Point Approach
-Homomorphisms: A Fixed Point Approach
Fixed Point Theory and Applications volume 2011, Article number: 454093 (2011)
Abstract
Using fixed point methods, we prove the stability and superstability of  -ternary additive, quadratic, cubic, and quartic homomorphisms in
-ternary additive, quadratic, cubic, and quartic homomorphisms in  -ternary rings for the functional equation
-ternary rings for the functional equation  , for each
, for each  .
.
1. Introduction
Following the terminology of [1], a nonempty set  with a ternary operation
with a ternary operation  is called a ternary groupoid, which is denoted by
is called a ternary groupoid, which is denoted by  . The ternary groupoid
. The ternary groupoid  is said to be commutative if
is said to be commutative if  for all
for all  and all permutations
and all permutations  of
of  . If a binary operation
. If a binary operation  is defined on
is defined on  such that
such that  for all
for all  , then we say that
, then we say that  is derived from
is derived from  . We say that
. We say that  is a ternary semigroup if the operation
is a ternary semigroup if the operation  is associative, that is, if
is associative, that is, if  holds for all
holds for all  (see [2]). Since it is extensively discussed in [3], the full description of a physical system
(see [2]). Since it is extensively discussed in [3], the full description of a physical system  implies the knowledge of three basis ingredients: the set of the observables, the set of the states, and the dynamics that describes the time evolution of the system by means of the time dependence of the expectation value of a given observable on a given statue. Originally, the set of the observable was considered to be a
implies the knowledge of three basis ingredients: the set of the observables, the set of the states, and the dynamics that describes the time evolution of the system by means of the time dependence of the expectation value of a given observable on a given statue. Originally, the set of the observable was considered to be a  -algebra [4]. In many applications, however, it was shown not to be the most convenient choice and the
-algebra [4]. In many applications, however, it was shown not to be the most convenient choice and the  -algebra was replaced by a von Neumann algebra because the role of the representation turns out to be crucial mainly when long-range interactions are involved (see [5] and references therein). Here we used a different algebraic structure.
-algebra was replaced by a von Neumann algebra because the role of the representation turns out to be crucial mainly when long-range interactions are involved (see [5] and references therein). Here we used a different algebraic structure.
A  -ternary ring is a complex Banach space
-ternary ring is a complex Banach space  , equipped with a ternary product
, equipped with a ternary product  of
of  into
into  , which is
, which is  -linear in the outer variables, conjugate
-linear in the outer variables, conjugate  -linear in the middle variable and associative in the sense that
-linear in the middle variable and associative in the sense that  and satisfies
and satisfies  and
and  .
.
If a  -ternary ring
-ternary ring  has an identity, that is, an element
has an identity, that is, an element  such that
such that  for all
for all  , then it is routine to verify that
, then it is routine to verify that  , endowed with
, endowed with  and
and  , is a unital
, is a unital  -algebra. Conversely, if
-algebra. Conversely, if  is a unital
is a unital  -algebra, then
-algebra, then  makes
makes  into a
into a  -ternary algebra.
-ternary algebra.
Consider the functional equation  in a certain general setting. A function
in a certain general setting. A function  is an approximate solution of
is an approximate solution of  if
if  and
and  are close in some sense. The Ulam stability problem asks whether or not there exists a true solution of
are close in some sense. The Ulam stability problem asks whether or not there exists a true solution of  near
near  . A functional equation is said to be superstable if every approximate solution of the equation is an exact solution of the functional equation. The problem of stability of functional equations originated from a question of Ulam [6] concerning the stability of group homomorphisms.
. A functional equation is said to be superstable if every approximate solution of the equation is an exact solution of the functional equation. The problem of stability of functional equations originated from a question of Ulam [6] concerning the stability of group homomorphisms.
Let  be a group and
be a group and  be a metric group with fthe metric
be a metric group with fthe metric  . Given
. Given  , does there exist a
, does there exist a  such that, if a mapping
such that, if a mapping  satisfies the inequality
satisfies the inequality

for all  , then there exists a homomorphism
, then there exists a homomorphism  with
with  for all
for all  ?
?
If the answer is affirmative, we say that the equation of homomorphism  is stable. The concept of stability for a functional equation arises when we replace the functional equation by an inequality which acts as a perturbation of the equation. Thus the stability question of functional equations is that how do the solutions of the inequality differ from those of the given functional equation?
is stable. The concept of stability for a functional equation arises when we replace the functional equation by an inequality which acts as a perturbation of the equation. Thus the stability question of functional equations is that how do the solutions of the inequality differ from those of the given functional equation?
In 1941, Hyers [7] gave a first affirmative answer to the question of Ulam for Banach spaces.
Let  and
and  be Banach spaces. Assume that
be Banach spaces. Assume that  satisfies
satisfies

for all  and some
and some  . Then there exists a unique additive mapping
. Then there exists a unique additive mapping  such that
such that  for all
for all  .
.
A generalized version of the theorem of Hyers for approximately additive mappings was given by Aoki [8] in 1950 (see also [9]). In 1978, a generalized solution for approximately linear mappings was given by Th. M. Rassias [10]. He considered a mapping  satisfying the condition
satisfying the condition

for all  , where
, where  and
and  . This result was later extended to all
. This result was later extended to all  and generalized by Gajda [11], Th. M. Rassias and Šemrl [12], and Isac and Th. M. Rassias [13].
and generalized by Gajda [11], Th. M. Rassias and Šemrl [12], and Isac and Th. M. Rassias [13].
In 2000, Lee and Jun [14] have improved the stability problem for approximately additive mappings. The problem when  is not true. Counter examples for the corresponding assertion in the case
is not true. Counter examples for the corresponding assertion in the case  were constructed by Gadja [11], Th. M. Rassias and Šemrl [12].
were constructed by Gadja [11], Th. M. Rassias and Šemrl [12].
On the other hand, J. M. Rassias [15–17] considered the Cauchy difference controlled by a product of different powers of norm. Furthermore, a generalization of Th. M. Rassias theorems was obtained by Găvruţa [18], who replaced

and  by a general control function
by a general control function  . In 1949 and 1951, Bourgin [19, 20] is the first mathematician dealing with stability of (ring) homomorphism
. In 1949 and 1951, Bourgin [19, 20] is the first mathematician dealing with stability of (ring) homomorphism  . The topic of approximation of functional equations on Banach algebras was studied by a number of mathematicians (see [21–33]).
. The topic of approximation of functional equations on Banach algebras was studied by a number of mathematicians (see [21–33]).
The functional equation:

is related to a symmetric biadditive mapping [34, 35]. It is natural that this equation is called a quadratic functional equation. For more details about various results concerning such problems, the readers refer to [36–43].
In 2002, Jun and Kim [44] introduced the following cubic functional equation:

and they established the general solution and the generalized Hyers-Ulam-Rassias stability for the functional equation (1.6). Obviously, the mapping  satisfies the functional equation (1.6), which is called the cubic functional equation. In 2005, Lee et al. [45] considered the following functional equation
satisfies the functional equation (1.6), which is called the cubic functional equation. In 2005, Lee et al. [45] considered the following functional equation

It is easy to see that the mapping  is a solution of the functional equation (1.7), which is called the quartic functional equation.
is a solution of the functional equation (1.7), which is called the quartic functional equation.
2. Preliminaries
In 2007, Park and Cui [46] investigated the generalized stability of a quadratic mapping  , which is called a
, which is called a  -ternary quadratic mapping if
-ternary quadratic mapping if  is a quadratic mapping satisfies
is a quadratic mapping satisfies

for all  . Let
. Let  be a
be a  -ternary ring derived from a unital commutative
-ternary ring derived from a unital commutative  -algebra
-algebra  and let
and let  satisfy
satisfy  for all
for all  . It is easy to show that the mapping
. It is easy to show that the mapping  is a
is a  -ternary quadratic mapping.
-ternary quadratic mapping.
Recently, in 2010, Bae and Park [47] investigated the following functional equations

for each  , and
, and

and they have obtained the stability of the functional equations (2.2) and (2.3).
We can rewrite the functional equations (2.2) and (2.3) by

Obviously, the monomial  is a solution of the functional equation (2.4) for each
is a solution of the functional equation (2.4) for each  .
.
For  , Bae and Park [47, 48] showed that the functional equation (2.4) is equivalent to the additive equation and quadratic equation, respectively.
, Bae and Park [47, 48] showed that the functional equation (2.4) is equivalent to the additive equation and quadratic equation, respectively.
If  , the functional equation (2.4) is equivalent to the cubic equation [44]. Moreover, Lee et al. [45] solved the solution of the functional equation (2.4) for
, the functional equation (2.4) is equivalent to the cubic equation [44]. Moreover, Lee et al. [45] solved the solution of the functional equation (2.4) for  .
.
In this paper, using the idea of Park and Cui [46], we study the further generalized stability of  -ternary additive, quadratic, cubic, and quartic mappings over
-ternary additive, quadratic, cubic, and quartic mappings over  -ternary algebra via fixed point method for the functional equation (2.4). Moreover, we establish the superstability of this functional equation by suitable control functions.
-ternary algebra via fixed point method for the functional equation (2.4). Moreover, we establish the superstability of this functional equation by suitable control functions.
Definition 2.1.
Let  and
and  be two
be two  -ternary algebras.
-ternary algebras.
(1)A mapping  is called a
is called a  -ternary additive homomorphism
-ternary additive homomorphism briefly,
briefly,  -ternary 1-homomorphism
-ternary 1-homomorphism if
if  is an additive mapping satisfying (2.1) for all
is an additive mapping satisfying (2.1) for all  .
.
(2)A mapping  is called a
is called a  -ternary quadratic mapping
-ternary quadratic mapping briefly,
briefly,  -ternary 2-homomorphism
-ternary 2-homomorphism if
if  is a quadratic mapping satisfying (2.1) for all
is a quadratic mapping satisfying (2.1) for all  .
.
(3)A mapping  is called a
is called a  -ternary cubic mapping
-ternary cubic mapping briefly,
briefly,  -ternary 3-homomorphism
-ternary 3-homomorphism if
if  is a cubic mapping satisfying (2.1) for all
is a cubic mapping satisfying (2.1) for all  .
.
(4)A mapping  is called a
is called a  -ternary quartic homomorphism
-ternary quartic homomorphism briefly,
briefly,  -ternary 4-homomorphism
-ternary 4-homomorphism if
if  is a quartic mapping satisfying (2.1) for all
is a quartic mapping satisfying (2.1) for all  .
.
Now, we state the following notion of fixed point theorem. For the proof, refer to [49] (see also Chapter 5 in [50] and [51, 52]). In 2003, Radu [53] proposed a new method for obtaining the existence of exact solutions and error estimations, based on the fixed point alternative (see also [54–57]).
Let  be a generalized metric space. We say that a mapping
be a generalized metric space. We say that a mapping  satisfies a Lipschitz condition if there exists a constant
satisfies a Lipschitz condition if there exists a constant  such that
such that  for all
for all  , where the number
, where the number  is called the Lipschitz constant. If the Lipschitz constant
is called the Lipschitz constant. If the Lipschitz constant  is less than 1, then the mapping
is less than 1, then the mapping  is called a strictly contractive mapping. Note that the distinction between the generalized metric and the usual metric is that the range of the former is permitted to include the infinity.
is called a strictly contractive mapping. Note that the distinction between the generalized metric and the usual metric is that the range of the former is permitted to include the infinity.
The following theorem was proved by Diaz and Margolis [49] and Radu [53].
Theorem 2.2.
Suppose that  is a complete generalized metric space and
is a complete generalized metric space and  is a strictly contractive mapping with the Lipschitz constant
is a strictly contractive mapping with the Lipschitz constant  . Then, for any
. Then, for any  , either
, either

or there exists a natural number  such that
such that
(1) for all
for all  ;
;
(2)the sequence  is convergent to a fixed point
is convergent to a fixed point  of
of  ;
;
(3) is the unique fixed point of
is the unique fixed point of  in
in  ;
;
(4) for all
for all  .
.
3. Approximation of  -Ternary
-Ternary 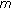 -Homomorphisms between
-Homomorphisms between 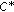 -Ternary Algebras
-Ternary Algebras
In this section, we investigate the generalized stability of  -ternary
-ternary  -homomorphism between
-homomorphism between  -ternary algebras for the functional equation (2.4).
-ternary algebras for the functional equation (2.4).
Throughout this section, we suppose that  and
and  are two
are two  -ternary algebras. For convenience, we use the following abbreviation: for any function
-ternary algebras. For convenience, we use the following abbreviation: for any function  ,
,

for all  .
.
From now on, let  be a positive integer less than 5.
be a positive integer less than 5.
Theorem 3.1.
Let  be a mapping for which there exist functions
be a mapping for which there exist functions  and
and  such that
such that


for all  . If there exists a constant
. If there exists a constant  such that
such that

for all  , then there exists a unique
, then there exists a unique  -ternary
-ternary  -homomorphism
-homomorphism  such that
such that

for all  .
.
Proof.
It follows from (3.4) that


for all  . By (3.6),
. By (3.6),  and so
and so  . Letting
. Letting  in (3.2), we get
in (3.2), we get  and so
and so  .
.
Let  . We introduce a generalized metric on
. We introduce a generalized metric on  as follows:
as follows:

It is easy to show that  is a generalized complete metric space [55].
is a generalized complete metric space [55].
Now, we consider the mapping  defined by
defined by  for all
for all  and
and  . Note that, for all
. Note that, for all  and
and  ,
,

Hence we see that

for all  , that is,
, that is,  is a strictly self-mapping of
is a strictly self-mapping of  with the Lipschitz constant
with the Lipschitz constant  . Putting
. Putting  in (3.2), we have
in (3.2), we have

for all  and so
and so

for all  , that is,
, that is,  .
.
Now, from Theorem 2.2, it follows that there exists a fixed point  of
of  in
in  such that
such that

for all  since
since  .
.
On the other hand, it follows from (3.2), (3.6), and (3.13) that

for all  and so
and so  . By the result in [44, 45, 47],
. By the result in [44, 45, 47],  is
is  -mapping and so it follows from the definition of
-mapping and so it follows from the definition of  , (3.3) and (3.7) that
, (3.3) and (3.7) that

for all  and so
and so  .
.
According to Theorem 2.2, since  is the unique fixed point of
is the unique fixed point of  in the set
in the set  ,
,  is the unique mapping such that
is the unique mapping such that

for all  and
and  . Again, using Theorem 2.2, we have
. Again, using Theorem 2.2, we have

and so

for all  . This completes the proof.
. This completes the proof.
Corollary 3.2.
Let  be nonnegative real numbers with
be nonnegative real numbers with  and
and  . Suppose that
. Suppose that  is a mapping such that
is a mapping such that


for all  . Then there exists a unique
. Then there exists a unique  -ternary
-ternary  -homomorphism
-homomorphism  satisfying
satisfying

for all  .
.
Proof.
The proof follows from Theorem 3.1 by taking

for all  . Then we can choose
. Then we can choose  and so the desired conclusion follows.
and so the desired conclusion follows.
Remark 3.3.
Let  be a mapping with
be a mapping with  such that there exist functions
such that there exist functions  and
and  satisfying (3.2) and (3.3). Let
satisfying (3.2) and (3.3). Let  be a constant such that
be a constant such that

for all  . By the similar method as in the proof of Theorem 3.1, one can show that there exists a unique
. By the similar method as in the proof of Theorem 3.1, one can show that there exists a unique  -ternary
-ternary  -homomorphism
-homomorphism  satisfying
satisfying

for all  . For the case
. For the case

where  ,
,  are nonnegative real numbers and
are nonnegative real numbers and  ,
,  and
and  , there exists a unique
, there exists a unique  -ternary
-ternary  -homomorphism
-homomorphism  satisfying
satisfying

for all  .
.
In the following, we formulate and prove a theorem in superstability of  -ternary
-ternary  -homomorphism in
-homomorphism in  -ternary rings for the functional equation (2.4).
-ternary rings for the functional equation (2.4).
Theorem 3.4.
Suppose that there exist functions  ,
,  and a constant
and a constant  such that
such that

for all  . Moreover, if
. Moreover, if  is a mapping such that
is a mapping such that


for all  , then
, then  is a
is a  -ternary
-ternary  -homomorphism.
-homomorphism.
Proof.
It follows from (3.27) that


for all  . We have
. We have  since
since  . Letting
. Letting  in (3.28), we get
in (3.28), we get  for all
for all  . By using induction, we obtain
. By using induction, we obtain

for all  and
and  and so
and so

for all  and
and  . It follows from (3.29) and (3.33) that
. It follows from (3.29) and (3.33) that

for all  , and
, and  . Hence, letting
. Hence, letting  in (3.34) and using (3.31), we have
in (3.34) and using (3.31), we have  for all
for all  .
.
On the other hand, we have

for all  and
and  . Thus, letting
. Thus, letting  in (3.35) and using (3.30), we have
in (3.35) and using (3.30), we have  for all
for all  . Therefore,
. Therefore,  is a
is a  -ternary
-ternary  -homomorphism. This completes the proof.
-homomorphism. This completes the proof.
Corollary 3.5.
Let  ,
,  ,
,  be nonnegative real numbers with
be nonnegative real numbers with  and
and  . If
. If  is a function such that
is a function such that

for all  , then
, then  is a
is a  -ternary
-ternary  -homomorphism.
-homomorphism.
Remark 3.6.
Let  be nonnegative real numbers with
be nonnegative real numbers with  . Suppose that there exists a function
. Suppose that there exists a function  and a constant
and a constant  such that
such that

for all  . Moreover, if
. Moreover, if  is a mapping such that
is a mapping such that

for all  , then
, then  is a
is a  -ternary
-ternary  -homomorphism.
-homomorphism.
In the rest of this section, assume that  is a unital
is a unital  -ternary algebra with the unit
-ternary algebra with the unit  and
and  is a
is a  -ternary algebra with the unit
-ternary algebra with the unit  .
.
Theorem 3.7.
Let  ,
,  ,
,  be positive real numbers with
be positive real numbers with  ,
,  and
and  . Suppose that
. Suppose that  is a mapping satisfying (3.19) and (3.20). If there exist a real number
is a mapping satisfying (3.19) and (3.20). If there exist a real number  and
and  such that
such that  , then the mapping
, then the mapping  is a
is a  -ternary
-ternary  -homomorphism.
-homomorphism.
Proof.
By Corollary 3.2, there exists a unique  -ternary
-ternary  -homomorphism
-homomorphism  such that
such that

for all  . It follows from (3.39) that
. It follows from (3.39) that

for all  and
and  . Therefore, by the assumption, we get that
. Therefore, by the assumption, we get that  .
.
Let  and
and  . It follows from (3.20) that
. It follows from (3.20) that

for all  and so
and so  for all
for all  . Letting
. Letting  in the last equality, we get
in the last equality, we get  for all
for all  .
.
Similarly, one can show that  for all
for all  when
when  and
and  . Therefore, the mapping
. Therefore, the mapping  is a
is a  -ternary
-ternary  -homomorphism. This completes the proof.
-homomorphism. This completes the proof.
Theorem 3.8.
Let  be positive real numbers with
be positive real numbers with  and
and  and
and  . Suppose that
. Suppose that  is a mapping satisfying (3.19) and
is a mapping satisfying (3.19) and

for all  . If there exist a real number
. If there exist a real number  and
and  such that
such that  , then the mapping
, then the mapping  is a
is a  -ternary
-ternary  -homomorphism.
-homomorphism.
Proof.
By Theorem 3.1 there exists a unique  -ternary
-ternary  -homomorphism
-homomorphism  such that
such that

for all  . It follows from (3.43) that
. It follows from (3.43) that

for all  and
and  . Therefore, by the assumption, we get that
. Therefore, by the assumption, we get that  .
.
Let  and
and  . It follows from (3.20) that
. It follows from (3.20) that

for all  and so
and so  for all
for all  . Letting
. Letting  in the last equality, we get
in the last equality, we get  for all
for all  .
.
Similarly, one can show that  for all
for all  when
when  and
and  . Therefore, the mapping
. Therefore, the mapping  is a
is a  -ternary
-ternary  -homomorphism. This completes the proof.
-homomorphism. This completes the proof.
References
Duplij S: Ternary Hopf algebras. In Symmetry in Nonlinear Mathematical Physics, Natsīonal'noï Akademīï Nauk Ukraïni Mat. Zastos., 43, Part 1, 2; Natsīonal'noï Akademīï Nauk Ukraïni, Institute of Mathematics, Kyiv. Volume 2. Natsīonal'noï Akademīï Nauk Ukraïni, Kiev, Ukraine; 2002:439–448.
Bazunova N, Borowiec A, Kerner R: Universal differential calculus on ternary algebras. Letters in Mathematical Physics 2004,67(3):195–206.
Sewell GL: Quantum Mechanics and Its Emergent Macrophysics. Princeton University Press, Princeton, NJ, USA; 2002:xii+292.
Haag R, Kastler D: An algebraic approach to quantum field theory. Journal of Mathematical Physics 1964, 5: 848–861. 10.1063/1.1704187
Bagarello F, Morchio G: Dynamics of mean-field spin models from basic results in abstract differential equations. Journal of Statistical Physics 1992,66(3–4):849–866. 10.1007/BF01055705
Ulam SM: Problems in Modern Mathematics. John Wiley & Sons, New York, NY, USA; 1964:xvii+150.
Hyers DH: On the stability of the linear functional equation. Proceedings of the National Academy of Sciences of the United States of America 1941, 27: 222–224. 10.1073/pnas.27.4.222
Aoki T: On the stability of the linear transformation in Banach spaces. Journal of the Mathematical Society of Japan 1950, 2: 64–66. 10.2969/jmsj/00210064
Bourgin DG: Classes of transformations and bordering transformations. Bulletin of the American Mathematical Society 1951, 57: 223–237. 10.1090/S0002-9904-1951-09511-7
Rassias ThM: On the stability of the linear mapping in Banach spaces. Proceedings of the American Mathematical Society 1978,72(2):297–300. 10.1090/S0002-9939-1978-0507327-1
Gajda Z: On stability of additive mappings. International Journal of Mathematics and Mathematical Sciences 1991,14(3):431–434. 10.1155/S016117129100056X
Rassias ThM, Šemrl P: On the behavior of mappings which do not satisfy Hyers-Ulam stability. Proceedings of the American Mathematical Society 1992,114(4):989–993. 10.1090/S0002-9939-1992-1059634-1
Isac G, Rassias ThM: On the Hyers-Ulam stability of -additive mappings. Journal of Approximation Theory 1993,72(2):131–137. 10.1006/jath.1993.1010
Lee Y-H, Jun K-W: On the stability of approximately additive mappings. Proceedings of the American Mathematical Society 2000,128(5):1361–1369. 10.1090/S0002-9939-99-05156-4
Rassias JM: On approximation of approximately linear mappings by linear mappings. Journal of Functional Analysis 1982,46(1):126–130. 10.1016/0022-1236(82)90048-9
Rassias JM: On approximation of approximately linear mappings by linear mappings. Bulletin des Sciences Mathématiques 1984,108(4):445–446.
Rassias JM: Solution of a problem of Ulam. Journal of Approximation Theory 1989,57(3):268–273. 10.1016/0021-9045(89)90041-5
Găvruţa P: A generalization of the Hyers-Ulam-Rassias stability of approximately additive mappings. Journal of Mathematical Analysis and Applications 1994,184(3):431–436. 10.1006/jmaa.1994.1211
Bourgin DG: Classes of transformations and bordering transformations. Bulletin of the American Mathematical Society 1951, 57: 223–237. 10.1090/S0002-9904-1951-09511-7
Bourgin DG: Approximately isometric and multiplicative transformations on continuous function rings. Duke Mathematical Journal 1949, 16: 385–397. 10.1215/S0012-7094-49-01639-7
Badora R: On approximate ring homomorphisms. Journal of Mathematical Analysis and Applications 2002,276(2):589–597. 10.1016/S0022-247X(02)00293-7
Baker J, Lawrence J, Zorzitto F: The stability of the equation . Proceedings of the American Mathematical Society 1979, 74: 242–246.
Savadkouhi MB, Gordji ME, Rassias JM, Ghobadipour N: Approximate ternary Jordan derivations on Banach ternary algebras. Journal of Mathematical Physics 2009,50(4, article 042303):-9.
Eshaghi Gordji M, Najati A: Approximately -homomorphisms: a fixed point approach. Journal of Geometry and Physics 2010,60(5):809–814. 10.1016/j.geomphys.2010.01.012
Park C-G: Homomorphisms between Lie -algebras and Cauchy-Rassias stability of Lie -algebra derivations. Journal of Lie Theory 2005,15(2):393–414.
Eshaghi Gordji M, Ghaemi MB, Kaboli Gharetapeh S, Shams S, Ebadian A: On the stability of -derivations. Journal of Geometry and Physics 2010,60(3):454–459. 10.1016/j.geomphys.2009.11.004
Eshaghi Gordji M, Kaboli Gharetapeh S, Rashidi E, Karimi T, Aghaei M: Ternary Jordan -derivations in -ternary algebras. Journal of Computational Analysis and Applications 2010,12(2):463–470.
Park C, Gordji ME: Comment on "Approximate ternary Jordan derivations on Banach ternary algebras" [Bavand Savadkouhi et al., Journal of Mathematical Physics, vol. 50, article 042303, 2009]. Journal of Mathematical Physics 2010,51(4, article 044102):7.
Park C, Najati A: Generalized additive functional inequalities in Banach algebras. International Journal of Nonlinear Analysis and Applications 2010, 1: 54–62.
Park C, Rassias ThM: Isomorphisms in unital -algebras. International Journal of Nonlinear Analysis and Applications 2010, 1: 1–10.
Eshaghi Gordji M, Karimi T, Kaboli Gharetapeh S: Approximately -Jordan homomorphisms on Banach algebras. Journal of Inequalities and Applications 2009, 2009:-8.
Eshaghi Gordji M, Rassias JM, Ghobadipour N: Generalized Hyers-Ulam stability of generalized -derivations. Abstract and Applied Analysis 2009, 2009:-8.
Eshaghi Gordji M, Savadkouhi MB: Approximation of generalized homomorphisms in quasi-Banach algebras. Analele Stiintifice ale Universitatii Ovidius Constanta 2009,17(2):203–213.
Aczél J, Dhombres J: Functional Equations in Several Variables. Volume 31. Cambridge University Press, Cambridge, UK; 1989:xiv+462.
Kannappan P: Quadratic functional equation and inner product spaces. Results in Mathematics. Resultate der Mathematik 1995,27(3–4):368–372.
Czerwik S: On the stability of the quadratic mapping in normed spaces. Abhandlungen aus dem Mathematischen Seminar der Universität Hamburg 1992, 62: 59–64. 10.1007/BF02941618
Eshaghi Gordji M, Khodaei H: Solution and stability of generalized mixed type cubic, quadratic and additive functional equation in quasi-Banach spaces. Nonlinear Analysis. Theory, Methods & Applications 2009,71(11):5629–5643. 10.1016/j.na.2009.04.052
Eshaghi Gordji M, Khodaei H: On the generalized Hyers-Ulam-Rassias stability of quadratic functional equations. Abstract and Applied Analysis 2009, 2009:-11.
Forti GL: An existence and stability theorem for a class of functional equations. Stochastica 1980,4(1):23–30. 10.1080/17442508008833155
Forti G-L: Elementary remarks on Ulam-Hyers stability of linear functional equations. Journal of Mathematical Analysis and Applications 2007,328(1):109–118. 10.1016/j.jmaa.2006.04.079
Jung S-M: Hyers-Ulam-Rassias stability of Jensen's equation and its application. Proceedings of the American Mathematical Society 1998,126(11):3137–3143. 10.1090/S0002-9939-98-04680-2
Jung S-M: Hyers-Ulam-Rassias Stability of Functional Equations in Mathematical Analysis. Hadronic Press, Palm Harbor, Fla, USA; 2001:ix+256.
Khodaei H, Rassias ThM: Approximately generalized additive functions in several variables. International Journal of Nonlinear Analysis 2010, 1: 22–41.
Jun K-W, Kim H-M: The generalized Hyers-Ulam-Rassias stability of a cubic functional equation. Journal of Mathematical Analysis and Applications 2002,274(2):867–878. 10.1016/S0022-247X(02)00415-8
Lee SH, Im SM, Hwang IS: Quartic functional equations. Journal of Mathematical Analysis and Applications 2005,307(2):387–394. 10.1016/j.jmaa.2004.12.062
Park C, Cui J: Generalized stability of -ternary quadratic mappings. Abstract and Applied Analysis 2007, 2007:-6.
Bae J-H, Park W-G: A functional equation having monomials as solutions. Applied Mathematics and Computation 2010,216(1):87–94. 10.1016/j.amc.2010.01.006
Bae J-H, Park W-G: On a cubic equation and a Jensen-quadratic equation. Abstract and Applied Analysis 2007, 2007:-10.
Diaz JB, Margolis B: A fixed point theorem of the alternative, for contractions on a generalized complete metric space. Bulletin of the American Mathematical Society 1968, 74: 305–309. 10.1090/S0002-9904-1968-11933-0
Rus IA: Principles and Applications of Fixed Point Theory. , Cluj-Napoca; 1979.
Hyers DH, Isac G, Rassias ThM: Stability of Functional Equations in Several Variables. Birkhäuser Boston Inc., Boston, Mass, USA; 1998:vi+313.
Zeidler E: Nonlinear functional analysis and its applications. In Fixed-Point Theorems. 2. Volume 1. Springer; 1993:xxiii +909.
Radu V: The fixed point alternative and the stability of functional equations. Fixed Point Theory 2003,4(1):91–96.
Cădariu L, Radu V: Fixed points and the stability of Jensen's functional equation. Journal of Inequalities in Pure and Applied Mathematics 2003,4(1, article 4):7.
Cădariu L, Radu V: On the stability of the Cauchy functional equation: a fixed point approach. In Iteration Theory, Grazer Mathematische Berichte. Volume 346. Karl-Franzens-Universitaet Graz, Graz, Austria; 2004:43–52.
Ebadian A, Ghobadipour N, Gordji ME: A fixed point method for perturbation of bimultipliers and Jordan bimultipliers in -ternary algebras. Journal of Mathematical Physics 2010, 51:-10.
Eshaghi Gordji M, Khodaei H: The fixed point method for fuzzy approximation of a functional equation associated with inner product spaces. Discrete Dynamics in Nature and Society 2010, 2010:-15.
Acknowledgment
This work was supported by the Korea Research Foundation Grant funded by the Korean Government (KRF-2008-313-C00050).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License ( https://creativecommons.org/licenses/by/2.0 ), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Gordji, M., Alizadeh, Z., Cho, Y. et al. On Approximate 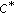 -Ternary
-Ternary 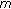 -Homomorphisms: A Fixed Point Approach.
Fixed Point Theory Appl 2011, 454093 (2011). https://doi.org/10.1155/2011/454093
-Homomorphisms: A Fixed Point Approach.
Fixed Point Theory Appl 2011, 454093 (2011). https://doi.org/10.1155/2011/454093
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/454093
 -Ternary
-Ternary 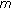 -Homomorphisms between
-Homomorphisms between 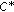 -Ternary Algebras
-Ternary Algebras