- Research Article
- Open access
- Published:
Existence and Stability of Solutions for Implicit Multivalued Vector Equilibrium Problems
Fixed Point Theory and Applications volume 2011, Article number: 381218 (2011)
Abstract
A class of implicit multivalued vector equilibrium problems is studied. By using the generalized Fan-Browder fixed point theorem, some existence results of solutions for the implicit multivalued vector equilibrium problems are obtained under some suitable assumptions. Moreover, a stability result of solutions for the implicit multivalued vector equilibrium problems is derived. These results extend and unify some recent results for implicit vector equilibrium problems, multivalued vector variational inequality problems, and vector variational inequality problems.
1. Introduction
Let  be a Hausdorff topological vector space,
be a Hausdorff topological vector space,  a nonempty subset of
a nonempty subset of  , and
, and  a function. Then, the scalar equilibrium problem consists in finding
a function. Then, the scalar equilibrium problem consists in finding  such that
such that

This problem provides a unifying framework for many important problems, such as, optimization problems, variational inequality problems, complementary problems, minimal inequality problems, and fixed point problems, and has been widely applied to study the problems arising in economics, mechanics, and engineering science (see [1]). In recent years, lots of existence results concerning equilibrium problems and variational inequality problems have been established by many authors in different ways. For details, we refer the reader to [1–26] and the references therein.
Now, let  be another Hausdorff topological vector space and
be another Hausdorff topological vector space and  a closed convex cone with
a closed convex cone with  , where
, where  denotes the topological interior of
denotes the topological interior of  . Let
. Let  be a given map. Recently, Ansari et al. [2] studied the following vector equilibrium problems to find
be a given map. Recently, Ansari et al. [2] studied the following vector equilibrium problems to find  such that
such that

or to find  such that
such that

In case that the map  is multivalued, Ansari et al. [2] also studied the following multivalued vector equilibrium problem (for short, MVEP) to find
is multivalued, Ansari et al. [2] also studied the following multivalued vector equilibrium problem (for short, MVEP) to find  such that
such that

or to find  such that
such that

By using an abstract monotonicity condition, they gave some existence theorems of solutions for MVEP.
Very recently, in [3, 4], the authors studied the following implicit vector equilibrium problems (for short, IVEP): to find  such that
such that

where  is a vector-valued map and
is a vector-valued map and  is a multivalued map such that, for all
is a multivalued map such that, for all  ,
,  is a closed convex cone in
is a closed convex cone in  with
with  . By using the famous FKKM theorem and section theorem, they gave some existence results of solutions for IVEP.
. By using the famous FKKM theorem and section theorem, they gave some existence results of solutions for IVEP.
Inspired and motivated by the research work mentioned above, in this paper, we consider a class of implicit multivalued vector equilibrium problems and introduce the concepts of  -pseudomonotonicity and
-pseudomonotonicity and  -hemicontinuity for multivalued maps. By using the fixed point theorem of Chowdhury and Tan [27], we obtain some existence results of solutions for the implicit multivalued vector equilibrium problems in the setting of topological vector spaces. Furthermore, we derive a stability result of solutions for the implicit multivalued vector equilibrium problems. These results extend and unify some recent results for implicit vector equilibrium problems, multivalued vector variational inequality problems, and vector variational inequality problems.
-hemicontinuity for multivalued maps. By using the fixed point theorem of Chowdhury and Tan [27], we obtain some existence results of solutions for the implicit multivalued vector equilibrium problems in the setting of topological vector spaces. Furthermore, we derive a stability result of solutions for the implicit multivalued vector equilibrium problems. These results extend and unify some recent results for implicit vector equilibrium problems, multivalued vector variational inequality problems, and vector variational inequality problems.
2. Preliminaries
Throughout this paper, unless otherwise specified, we suppose that  ,
,  , and
, and  are topological vector spaces, and
are topological vector spaces, and  and
and  are nonempty subsets. We also suppose that
are nonempty subsets. We also suppose that  is a multivalued map such that, for any
is a multivalued map such that, for any  ,
,  is a proper, closed, and convex cone in
is a proper, closed, and convex cone in  with
with  ,
,  ,
,  are vector-valued maps, and
are vector-valued maps, and  ,
,  are multivalued maps.
are multivalued maps.
In this paper, we consider the following implicit multivalued vector equilibrium problem (for short, IMVEP) to find  such that
such that

We call this  a solution for IMVEP.
a solution for IMVEP.
Some special cases of IMVEP.
(1)If  is a single-valued map, then IMVEP reduces to the problem of finding
is a single-valued map, then IMVEP reduces to the problem of finding  such that
such that

which has been studied in [5].
(2)If  is a single-valued map,
is a single-valued map,  , then IMVEP reduces to IVEP.
, then IMVEP reduces to IVEP.
(3)If  is a single-valued map,
is a single-valued map,  , then IMVEP reduces to the problem of finding
, then IMVEP reduces to the problem of finding  such that
such that

which has been studied in [6].
(4)If  ,
,  (
( is a closed convex cone in
is a closed convex cone in  with
with  ), then IMVEP reduces to MVEP.
), then IMVEP reduces to MVEP.
Definition 2.1 (see[28]).
Let  and
and  be two topological spaces. A multivalued map
be two topological spaces. A multivalued map  is said to be
is said to be
(i)upper semicontinuous (for short, u.s.c.) at  if, for each open set
if, for each open set  in
in  with
with  , there exists an open neighborhood
, there exists an open neighborhood  of
of  such that
such that  for all
for all  ;
;
(ii)lower semicontinuous (for short, l.s.c.) at  if, for each open set
if, for each open set  in
in  with
with  , there exists an open neighborhood
, there exists an open neighborhood  of
of  such that
such that  for all
for all  ;
;
(iii)closed if the graph  is a closed subset of
is a closed subset of  .
.
(iv)compact-valued if, for each  ,
,  is a nonempty compact subset of
is a nonempty compact subset of  .
.
Definition 2.2.
Let  and
and  be topological vector spaces,
be topological vector spaces,  a nonempty convex subset of
a nonempty convex subset of  and
and  a nonempty convex cone of
a nonempty convex cone of  . A multivalued map
. A multivalued map  is said to be
is said to be  -convex if, for any
-convex if, for any  and
and  , one has
, one has

Definition 2.3.
Let  ,
,  , and
, and  be topological vector spaces,
be topological vector spaces,  a nonempty convex subset of
a nonempty convex subset of  , and
, and  a nonempty subset of
a nonempty subset of  . Let
. Let  be a multivalued map such that, for any
be a multivalued map such that, for any  ,
,  is a proper, closed, and convex cone in
is a proper, closed, and convex cone in  with
with  . Given two vector-valued maps
. Given two vector-valued maps  ,
,  , and two multivalued maps
, and two multivalued maps  ,
,  . Then,
. Then,  is said to be
is said to be
(i) -pseudomonotone with respect to
-pseudomonotone with respect to  and
and  on
on  if, for any
if, for any  and any
and any  ,
,  , one has
, one has

(ii)weakly  -pseudomonotone with respect to
-pseudomonotone with respect to  and
and  on
on  if, for any
if, for any  and any
and any  , one has
, one has

(iii) -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  on
on  if, for any
if, for any  ,
,  ,
,  and any
and any  , there exists
, there exists  such that, for any open set
such that, for any open set  with
with  , there exists
, there exists  such that
such that

Remark 2.4.
The above  -hemicontinuity for multivalued map is a generalization of
-hemicontinuity for multivalued map is a generalization of  -hemicontinuity for continuous linear operator.
-hemicontinuity for continuous linear operator.
Example 2.5.
Let  ,
,  , and
, and  for all
for all  . Let
. Let  ,
,  ,
,  and
and  be defined as follows:
be defined as follows:

Then,  is
is  -pseudomonotone with respect to
-pseudomonotone with respect to  and
and  on
on  . Moreover,
. Moreover,  is
is  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  on
on  .
.
Proof.
Firstly, we show that  is
is  -pseudomonotone with respect to
-pseudomonotone with respect to  and
and  on
on  .
.
Indeed, for any  ,
,  , and
, and  , it is obvious that
, it is obvious that  . If
. If

then,  , that is,
, that is,  . It follows that
. It follows that

Hence  is
is  -pseudomonotone with respect to
-pseudomonotone with respect to  and
and  on
on  .
.
Secondly, we show that  is
is  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  on
on  .
.
Indeed, let  . Taking
. Taking  , for any open set
, for any open set  with
with  , that is,
, that is,

there exists  such that
such that

Let  , for all
, for all  . Clearly,
. Clearly,  .
.
If  , then for any
, then for any  and any
and any  , we have
, we have

And so

If  , taking
, taking  , then for any
, then for any  and
and  , we have
, we have

It follows that

Thus,  is
is  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  on
on  .
.
Lemma 2.6 (see [29]).
Let  and
and  be two topological spaces and
be two topological spaces and  a multivalued map.
a multivalued map.
(i) is closed if and only if for any net
is closed if and only if for any net  with
with  and any net
and any net  such that
such that  with
with  , one has
, one has  .
.
(ii)If  is compact valued, then
is compact valued, then  is u.s.c. at
is u.s.c. at  if and only if for any net
if and only if for any net  with
with  and any net
and any net  with
with  , there exists
, there exists  and a subnet
and a subnet  such that
such that  .
.
The following lemma, which is a generalized form of Fan-Browder fixed piont theorem [30, 31], is very important to establish our existence results of solutions for IMVEP.
Lemma 2.7 (see [27]).
Let  be a nonempty convex subset of a topological vector space
be a nonempty convex subset of a topological vector space  and
and  be two multivalued maps such that
be two multivalued maps such that
(i)for any  ,
,  ;
;
(ii)for any  ,
,  is convex;
is convex;
(iii)for any  ,
,  is compactly open (i.e.,
is compactly open (i.e.,  is open in
is open in  for each nonempty compact subset
for each nonempty compact subset  of
of  );
);
(iv)there exists a nonempty, closed, and compact subset  and
and  such that
such that  ;
;
(v)for any  ,
,  .
.
Then, there exists  such that
such that  .
.
Lemma 2.8 (see [28]).
Let  and
and  be two Hausdorff topological vector spaces and
be two Hausdorff topological vector spaces and  a multivalued map. If
a multivalued map. If  is closed and
is closed and  is compact, then
is compact, then  is u.s.c., where
is u.s.c., where  and
and  denotes the closure of the set
denotes the closure of the set  .
.
Lemma 2.9 (see [32]).
Let  be a metric space and
be a metric space and  be compact subsets. If, for any open set
be compact subsets. If, for any open set  with
with  , there exists
, there exists  such that
such that  for all
for all  , then any sequence
, then any sequence  , satisfying
, satisfying  , for
, for  , has some subsequence which converges to some point of A.
, has some subsequence which converges to some point of A.
3. Existence of Solutions for IMVEP
In this section, we will apply the generalized Fan-Browder fixed point theorem to establish some existence results of solutions for IMVEP. First of all, we have the following lemma.
Lemma 3.1.
Let  ,
,  , and
, and  be topological vector spaces, and
be topological vector spaces, and  a nonempty convex subset of
a nonempty convex subset of  , and
, and  a nonempty subset of
a nonempty subset of  . Let
. Let  be a multivalued map such that, for any
be a multivalued map such that, for any  ,
,  is a proper, closed, and convex cone in
is a proper, closed, and convex cone in  with
with  . Given two vector-valued maps
. Given two vector-valued maps  ,
,  , and two multivalued maps
, and two multivalued maps  ,
,  . Consider the following problems.
. Consider the following problems.
(I)Find  such that,
such that,  ,
,  ;
;
(II)Find  such that,
such that,  ,
,  ;
;
(III)Find  such that,
such that,  ,
,  ;
;
Then,
(i)Problem (I) implies Problem (II) if  is weakly
is weakly  -pseudomonotone with respect to
-pseudomonotone with respect to  and
and  on
on  , moreover, implies Problem (III) if
, moreover, implies Problem (III) if  is
is  -pseudomonotone with respect to
-pseudomonotone with respect to  and
and  on
on  ;
;
(ii)Problem (II) implies Problem (I) if  is
is  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  on
on  and, for any
and, for any  and any
and any  ,
,  is
is  -convex and
-convex and  ;
;
(iii)Problem (III) implies Problem (II).
Proof.
-
(i)
It follows from the weakly
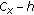 -pseudomonotone with respect to
-pseudomonotone with respect to 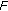 and
and 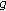 on
on  and
and 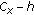 -pseudomonotone with respect to
-pseudomonotone with respect to 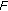 and
and  on
on 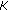 , respectively.
, respectively.
(ii)Let  be a solution of (II). Then,
be a solution of (II). Then,  ,
,  such that
such that

Let  , for all
, for all  . Since
. Since  is convex, we have
is convex, we have  . Then, there exists
. Then, there exists  such that
such that

Since for any  and any
and any  ,
,  is
is  -convex, we have
-convex, we have

Notice that for all  and any
and any  ,
,  . Then, we can obtain that
. Then, we can obtain that

Indeed, suppose to the contrary, that  for some
for some  , then
, then

which contradicts (3.2), and so (3.4) holds.
We claim that there exists  such that
such that

and so  is a solution of Problem (I).
is a solution of Problem (I).
In fact, if it is not the case, then we have, for any  ,
,  . And then it follows from the fact that
. And then it follows from the fact that  is
is  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  on
on  that there exists
that there exists  and
and  such that
such that  and
and

(3.7) contradicts (3.4), and so (3.6) holds.
-
(iii)
is obvious.
This completes the proof.
Now, we are ready to prove some existence theorems for IMVEP under suitable pseudomonotonicity assumptions.
Theorem 3.2.
Let  ,
,  , and
, and  be topological vector spaces, and
be topological vector spaces, and  a nonempty convex subset of
a nonempty convex subset of  and
and  a nonempty subset of
a nonempty subset of  . Let
. Let  be a multivalued map such that, for any
be a multivalued map such that, for any  ,
,  is a proper, closed, and convex cone in
is a proper, closed, and convex cone in  with
with  . Given two maps
. Given two maps  ,
,  , and two multivalued maps
, and two multivalued maps  ,
,  . Suppose the following conditions are satisfied:
. Suppose the following conditions are satisfied:
(i) is continuous in the first variable;
is continuous in the first variable;
(ii) is
is  -pseudomonotone and
-pseudomonotone and  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  on
on  ;
;
(iii)the multivalued map  , defined by
, defined by  is closed;
is closed;
(iv) is u.s.c. and compact-valued, and it satisfies the following conditions:
is u.s.c. and compact-valued, and it satisfies the following conditions:
(a)for any  and
and  ,
,  is
is  -convex and
-convex and  ;
;
(b)for any  , there exists
, there exists  such that
such that  ;
;
-
(v)
there exists a nonempty, compact and closed subset
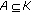 and
and  such that, for all
such that, for all 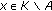 , one has
, one has

Then, IMVEP is solvable, that is, there exists  such that
such that

Proof.
Define two multivalued maps  as follows, for any
as follows, for any  ,
,

The proof is divided into the following steps.
-
(I)
For all
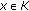 ,
,  .
.
Indeed, let  , then there exists
, then there exists  such that
such that

If  , then there exists
, then there exists  such that
such that

Since  is
is  -pseudomonotone with respect to
-pseudomonotone with respect to  and
and  on
on  , then, by (3.12), we have for all
, then, by (3.12), we have for all  ,
,

which contradicts (3.11). Thus,  , and so
, and so  .
.
-
(II)
For all
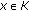 ,
, 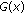 is convex.
is convex.
In fact, for any  and
and  , by the definition of
, by the definition of  , we have, for each
, we have, for each  ,
,

Let  . Since
. Since  is convex, we have
is convex, we have  . Noting that
. Noting that  is
is  -convex, we have
-convex, we have

By the arbitrary of  , we have
, we have  , and so
, and so  is convex.
is convex.
-
(III)
For any
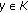 ,
, 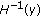 is compactly open.
is compactly open.
Indeed, for any given compact subset  , let
, let  . We will show that
. We will show that  is open in
is open in  by proving that
by proving that  is closed in
is closed in  . Let
. Let  be an arbitrary net such that
be an arbitrary net such that  . Then, for each
. Then, for each  ,
,  , that is,
, that is,  , thus, for any
, thus, for any  ,
,

It follows that, for each  , there exists
, there exists  such that
such that  , that is,
, that is,

Since  is continuous in the first variable and
is continuous in the first variable and  is u.s.c. and compact-valued, it follows from Lemma 2.6 that there exists
is u.s.c. and compact-valued, it follows from Lemma 2.6 that there exists  and a subnet of
and a subnet of  , we still denote this subnet by
, we still denote this subnet by  , such that
, such that  . Notice that
. Notice that  is closed. We have
is closed. We have  . It follows that
. It follows that  , and so
, and so

Then, by the arbitrary of  , we have
, we have  , that is,
, that is,  . Since
. Since  , we know that
, we know that  , and so
, and so  is closed in
is closed in  .
.
(IV)By the assumption (v), there exists a nonempty, compact, and closed subset  and
and  such that, for all
such that, for all  , we have
, we have

This implies that  , that is,
, that is,  . And thus
. And thus  .
.
-
(V)
 has no fixed point in
has no fixed point in 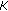 .
.
Suppose that it is not the case, then there exists  such that
such that  , that is,
, that is,

By the assumption (iv), we have  for some
for some  , and it follows that
, and it follows that  . This implies that
. This implies that  is an absorbing set in
is an absorbing set in  , which contradicts the assumption that
, which contradicts the assumption that  is proper in
is proper in  . Therefore,
. Therefore,  has no fixed point.
has no fixed point.
Since  has no fixed point in
has no fixed point in  , it follows from Lemma 2.7 that there exists
, it follows from Lemma 2.7 that there exists  such that
such that  , that is,
, that is,

From Lemma 3.1, we have  such that
such that

This completes the proof.
Remark 3.3.
Theorem 3.2 is a multivalued extension of [7, Theorem 3].
Remark 3.4.
The condition (v) of Theorem 3.2 is satisfied automatically if  is compact.
is compact.
We now give an example to illustrate Theorem 3.2.
Example 3.5.
Let  , and
, and  be as in Example 2.5. We will show that all conditions of Theorem 3.2 are satisfied.
be as in Example 2.5. We will show that all conditions of Theorem 3.2 are satisfied.
(I)It follows from Example 2.5 that the condition (ii) of Theorem 3.2 is satisfied. And it is obvious that  is compact valued and
is compact valued and  is a closed mapping.
is a closed mapping.
(II)We will show that  is u.s.c. on
is u.s.c. on  .
.
Let  , for any set
, for any set  with
with  .
.
(1)If  , then
, then  , and then there exists
, and then there exists  such that
such that  .
.
Taking  , then for any
, then for any  and
and  , we have
, we have

(2)If  , then
, then  , and then there exists
, and then there exists  such that
such that

Taking  and
and  , we have
, we have

It follows that for any  and any
and any  , then we have
, then we have  . Thus,
. Thus,

(3)If  , the argument is similar to (2).
, the argument is similar to (2).
Hence,  is u.s.c. on
is u.s.c. on  .
.
(III)We will show that for any  and
and  ,
,  is
is  -convex.
-convex.
For any  and
and  . Let
. Let  for each
for each  and
and  . Since
. Since

it follows that

Thus, we have

This shows that  is
is  -convex.
-convex.
(IV)Obviously, for any  and any
and any  ,
,

that is, for any  and
and  ,
,  .
.
For any  and
and  , we have
, we have

thus,  .
.
By the above arguments, we know that all the conditions of Theorem 3.2 are satisfied. By Theorem 3.2, IMVEP is solvable.
Indeed, let  , then for any
, then for any  , there exists
, there exists  such that
such that

Thus,  is a solution of IMVEP.
is a solution of IMVEP.
We now obtain an existence theorem for IMVEP for weakly  -pseudomonotone maps with respect to
-pseudomonotone maps with respect to  and
and  under additional assumptions.
under additional assumptions.
Theorem 3.6.
Let  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  be as in Theorem 3.2. Assume that the conditions (iii)–(v) of Theorem 3.2 and the following conditions are satisfied:
be as in Theorem 3.2. Assume that the conditions (iii)–(v) of Theorem 3.2 and the following conditions are satisfied:
 is continuous in the second variable and
is continuous in the second variable and  is continuous in the first variable;
is continuous in the first variable;
 is compact-valued, weakly
is compact-valued, weakly  -pseudomonotone and
-pseudomonotone and  -hemicontinuous with respect to
-hemicontinuous with respect to  and
and  on
on  .
.
Then, IMVEP is solvable, that is, there exists  such that
such that

Proof.
Define two multivalued maps  as follows, for any
as follows, for any  ,
,

By using the same arguments as in the proof (I) of Theorem 3.2 and weakly  -pseudomonotonicity with respect to
-pseudomonotonicity with respect to  and
and  on
on  of
of  , we see that for any
, we see that for any  ,
,  .
.
We have already seen in the proof of Theorem 3.2 that for each  ,
,  is convex and the multivalued map
is convex and the multivalued map  has no fixed point. Moreover, there exists a nonempty, compact, and closed subset
has no fixed point. Moreover, there exists a nonempty, compact, and closed subset  and
and  such that
such that  .
.
Next, we will show that, for each  ,
,  is compactly open.
is compactly open.
Indeed, for any given compact subset  , let
, let  . We will show that
. We will show that  is open in
is open in  by proving that
by proving that  is closed in
is closed in  . Let
. Let  be an arbitrary net such that
be an arbitrary net such that  . Then, for each
. Then, for each  ,
,  , that is,
, that is,  . Thus, for each
. Thus, for each  , there exists
, there exists  such that
such that

Since  is compact valued, there exists a subnet
is compact valued, there exists a subnet  of
of  such that
such that  . Then, by virtue of (3.35), for each
. Then, by virtue of (3.35), for each  , there exists
, there exists  such that
such that  , that is,
, that is,

Since  is continuous in the second variable and
is continuous in the second variable and  is continuous in the first variable, we have
is continuous in the first variable, we have

In addition,  is u.s.c. and compact valued, it follows from Lemma 2.6 that there exist
is u.s.c. and compact valued, it follows from Lemma 2.6 that there exist  and a subnet of
and a subnet of  , we still denote this subnet by
, we still denote this subnet by  , such that
, such that  . Notice that
. Notice that  is closed. We have
is closed. We have  . It follows that
. It follows that  , and so
, and so

Thus,  , that is,
, that is,  . Since
. Since  , we know that
, we know that  , and so
, and so  is closed in
is closed in  .
.
Hence, as in the proof of Theorem 3.2, there exists  such that
such that  , that is,
, that is,

From Lemma 3.1, we have  such that
such that

This completes the proof.
Remark 3.7.
Theorem 3.6 is a multivalued extension of [7, Theorem 4].
Next, we will prove an existence result for IMVEP without any kind of pseudomonotonicity assumption.
Theorem 3.8.
Let  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and
, and  be as in Theorem 3.2. Assume that the conditions (iii)–(v) of Theorem 3.2 and the following conditions are satisfied:
be as in Theorem 3.2. Assume that the conditions (iii)–(v) of Theorem 3.2 and the following conditions are satisfied:
 is continuous in both variables and
is continuous in both variables and  is continuous in the first variable;
is continuous in the first variable;
 is u.s.c. and compact-valued.
is u.s.c. and compact-valued.
Then, IMVEP is solvable, that is, there exists  such that
such that

Proof.
Define a multivalued map  as in the proof of Theorem 3.2. As we have seen in the proof in Theorem 3.2 that, for each
as in the proof of Theorem 3.2. As we have seen in the proof in Theorem 3.2 that, for each  ,
,  is convex and the multivalued map
is convex and the multivalued map  has no fixed point. Moreover, there exists a nonempty, compact, and closed subset
has no fixed point. Moreover, there exists a nonempty, compact, and closed subset  and
and  such that
such that  .
.
Now, we have only to show that, for any  ,
,  is compactly open.
is compactly open.
Indeed, for any given compact subset  , let
, let  . We will show that
. We will show that  is open in
is open in  by proving that
by proving that  is closed in
is closed in  . Let
. Let  be an arbitrary net such that
be an arbitrary net such that  . Then, for each
. Then, for each  ,
,  , that is,
, that is,  . Thus, for each
. Thus, for each  , there exists
, there exists  such that
such that

Since  is u.s.c. and compact-valued, it follow from Lemma 2.6 that there exists
is u.s.c. and compact-valued, it follow from Lemma 2.6 that there exists  and a subnet
and a subnet  such that
such that  . Then, by the assumption (i), we have
. Then, by the assumption (i), we have

Furthermore, by virtue of (3.42), for each  , there exists some
, there exists some  such that
such that  . It follows that
. It follows that

Since  is u.s.c. and compact-valued, it follows from Lemma 2.6 that there exist
is u.s.c. and compact-valued, it follows from Lemma 2.6 that there exist  and a subnet of
and a subnet of  , we still denote this subnet by
, we still denote this subnet by  such that
such that  . Notice that
. Notice that  is closed. We have
is closed. We have  , that is,
, that is,  , and so
, and so

Thus,  , that is,
, that is,  . Since
. Since  , we know that
, we know that  , and so
, and so  is closed in
is closed in  .
.
Thus, as in the proof of Theorem 3.2, there exists  such that
such that  , that is,
, that is,

This completes the proof.
Remark 3.9.
From the proof of Theorem 3.8, we can see that, if  is compact, then the condition
is compact, then the condition  can be replaced by the following condition
can be replaced by the following condition 
 is closed.
is closed.
4. Stability of Solution Sets for IMVEP
In this section, we discuss the stability of solutions for IMVEP.
Throughout this section, let  and
and  be Banach spaces, and
be Banach spaces, and  a topological vector space,
a topological vector space,  a nonempty compact convex subset and
a nonempty compact convex subset and  a nonempty subset, and
a nonempty subset, and  a multivalued map such that, for all
a multivalued map such that, for all  ,
,  is a proper, closed convex cone in
is a proper, closed convex cone in  with
with  .
.
Let

Let  be two compact sets in a normed space
be two compact sets in a normed space  . Recall the Hausdorff metric defined by
. Recall the Hausdorff metric defined by

For any given  , let
, let

where  is the Hausdorff metric. Then, it is easy to verify that
is the Hausdorff metric. Then, it is easy to verify that  is a metric space.
is a metric space.
Assume that the multivalued maps  and
and  satisfy all the conditions of Theorem 3.2. Then, it follows from Theorem 3.8 that for any
satisfy all the conditions of Theorem 3.2. Then, it follows from Theorem 3.8 that for any  , IMVEP has a solution, that is, there exists
, IMVEP has a solution, that is, there exists  such that
such that

Let

Then  , which implies that
, which implies that  is a multivalued map from
is a multivalued map from  into
into  .
.
Theorem 4.1.
 is an upper semicontinuous map with nonempty compact values.
is an upper semicontinuous map with nonempty compact values.
Proof.
Since  is compact, it follows from Lemma 2.8 that we need only to show that
is compact, it follows from Lemma 2.8 that we need only to show that  is closed. Let
is closed. Let  and
and  . We will show that
. We will show that  .
.
Indeed, for any  and
and  , since
, since  , there exists
, there exists  such that
such that

Notice that  and
and  are compact-valued. Then, for any open set
are compact-valued. Then, for any open set  with
with  , there exists
, there exists  such that
such that

where  . Since
. Since  and
and  is u.s.c., there exists
is u.s.c., there exists  such that, for all
such that, for all  ,
,


It follows from (4.8) that

By (4.10), (4.9), and (4.7), for all  , we have
, we have

Since  and for all
and for all  ,
,  , by Lemma 2.9, there exists a subsequence
, by Lemma 2.9, there exists a subsequence  of
of  such that
such that

Since  is continuous,
is continuous,  is continuous in the first variable, and
is continuous in the first variable, and  , we have
, we have

Then, it follows from (4.6) that

Thus, there exist  such that
such that  , that is,
, that is,  . Since
. Since  is u.s.c. and compact valued, there exist
is u.s.c. and compact valued, there exist  and a subsequence of
and a subsequence of  , we still denote this subsequence by
, we still denote this subsequence by  , such that
, such that  . Notice that
. Notice that  is closed. We have
is closed. We have  , that is,
, that is,  , and so
, and so

This implies that  , and so
, and so  is closed.
is closed.
This completes the proof.
5. Conclusions
In this paper, the existence and stability of solutions for a class of implicit multivalued vector equilibrium problems are studied. By using the generalized Fan-Browder fixed point theorem [27], some existence results of solutions for the implicit multivalued vector equilibrium problems are obtained under some suitable assumptions. These results generalize and extend some corresponding results of Ansari et al. [7]. Also, in Section 4 of this paper, a stability result of solutions for the implicit multivalued vector equilibrium problems is obtained. It is worth mentioning that, up till now, there is no paper to consider the stability of solutions for the implicit multivalued vector equilibrium problems. So, the stability result obtained in Section 4 of this paper is new and interesting.
References
Blum E, Oettli W: From optimization and variational inequalities to equilibrium problems. The Mathematics Student 1994,63(1–4):123–145.
Ansari QH, Oettli W, Schläger D: A generalization of vectorial equilibria. Mathematical Methods of Operations Research 1997,46(2):147–152. 10.1007/BF01217687
Huang NJ, Li J, Thompson HB: Implicit vector equilibrium problems with applications. Mathematical and Computer Modelling 2003,37(12–13):1343–1356. 10.1016/S0895-7177(03)90045-8
Li J, Huang N-J, Kim JK: On implicit vector equilibrium problems. Journal of Mathematical Analysis and Applications 2003,283(2):501–512. 10.1016/S0022-247X(03)00277-4
Chen X: Existence of solution for the implicit multi-valued vector equilibrium problem. Journal of Applied Mathematics and Computing 2009,30(1–2):469–478. 10.1007/s12190-008-0186-5
Ansari QH: Vector equilibrium problems and vector variational inequalities. In Vector Variational Inequalities and Vector Equilibria. Volume 38. Kluwer Academic, Dodrecht, The Netherlands; 2000:1–15. 10.1007/978-1-4613-0299-5_1
Ansari AH, Siddiqi AH, Yao J-C: Generalized vector variational-like inequalities and their scalarizations. In Vector Variational Inequalities and Vector Equilibria. Volume 38. Edited by: Giannessi F. Kluwer Academic, Dodrecht, The Netherlands; 2000:17–37. 10.1007/978-1-4613-0299-5_2
Ansari QH: Existence of solutions of systems of generalized implicit vector quasi-equilibrium problems. Journal of Mathematical Analysis and Applications 2008,341(2):1271–1283. 10.1016/j.jmaa.2007.11.033
Chen G-Y, Huang X, Yang Xiaoqi: Vector Optimization: Set-Valued and Variational Analysis. Volume 541. Springer, Berlin, Germany; 2005:x+306.
Chen GY, Yang XQ, Yu H: A nonlinear scalarization function and generalized quasi-vector equilibrium problems. Journal of Global Optimization 2005,32(4):451–466. 10.1007/s10898-003-2683-2
Fang Y-P, Huang N-J: Strong vector variational inequalities in Banach spaces. Applied Mathematics Letters 2006,19(4):362–368. 10.1016/j.aml.2005.06.008
Fang Y-P, Huang N-J: Vector equilibrium problems, minimal element problems and least element problems. Positivity 2007,11(2):251–268. 10.1007/s11117-006-2034-x
Fu J-Y: Generalized vector quasi-equilibrium problems. Mathematical Methods of Operations Research 2000,52(1):57–64. 10.1007/s001860000058
Fu JY: Stampacchia generalized vector quasiequilibrium problems and vector saddle points. Journal of Optimization Theory and Applications 2006,128(3):605–619. 10.1007/s10957-006-9034-7
Gong XH: Symmetric strong vector quasi-equilibrium problems. Mathematical Methods of Operations Research 2007,65(2):305–314. 10.1007/s00186-006-0114-0
Gong X-H: Optimality conditions for vector equilibrium problems. Journal of Mathematical Analysis and Applications 2008,342(2):1455–1466. 10.1016/j.jmaa.2008.01.026
Hou SH, Yu H, Chen GY: On system of generalized vector variational inequalities. Journal of Global Optimization 2008,40(4):739–749. 10.1007/s10898-006-9112-2
Huang NJ, Li J, Thompson HB: Stability for parametric implicit vector equilibrium problems. Mathematical and Computer Modelling 2006,43(11–12):1267–1274. 10.1016/j.mcm.2005.06.010
Huang NJ, Li J, Yao JC: Gap functions and existence of solutions for a system of vector equilibrium problems. Journal of Optimization Theory and Applications 2007,133(2):201–212. 10.1007/s10957-007-9202-4
Iusem AN, Kassay G, Sosa W: On certain conditions for the existence of solutions of equilibrium problems. Mathematical Programming 2009, 116: 259–273. 10.1007/s10107-007-0125-5
Li SJ, Teo KL, Yang XQ: Vector equilibrium problems with elastic demands and capacity constraints. Journal of Global Optimization 2007,37(4):647–660. 10.1007/s10898-006-9078-0
Lin L-J, Chuang C-S, Wang S-Y: From quasivariational inclusion problems to Stampacchia vector quasiequilibrium problems, Stampacchia set-valued vector Ekeland's variational principle and Caristi's fixed point theorem. Nonlinear Analysis. Theory, Methods & Applications 2009,71(1–2):179–185. 10.1016/j.na.2008.10.077
Lin Y-C: On generalized vector equilibrium problems. Nonlinear Analysis. Theory, Methods & Applications 2009,70(2):1040–1048. 10.1016/j.na.2008.01.030
Long X-J, Huang N-J, Teo K-L: Existence and stability of solutions for generalized strong vector quasi-equilibrium problem. Mathematical and Computer Modelling 2008,47(3–4):445–451. 10.1016/j.mcm.2007.04.013
Park S: Fixed points and quasi-equilibrium problems. Mathematical and Computer Modelling 2001,34(7–8):947–954. 10.1016/S0895-7177(01)00111-X
Wang SH, Fu JY: Stampacchia generalized vector quasi-equilibrium problem with set-valued mapping. Journal of Global Optimization 2009,44(1):99–110. 10.1007/s10898-008-9309-7
Chowdhury MSR, Tan K-K: Generalized variational inequalities for quasi-monotone operators and applications. Bulletin of the Polish Academy of Sciences Mathematics 1997,45(1):25–54.
Aubin J-P, Ekeland I: Applied Nonlinear Analysis. John Wiley & Sons, New York, NY, USA; 1984:xi+518.
Tan NX: Quasivariational inequalities in topological linear locally convex Hausdorff spaces. Mathematische Nachrichten 1985, 122: 231–245. 10.1002/mana.19851220123
Browder FE: The fixed point theory of multi-valued mappings in topological vector spaces. Mathematische Annalen 1968, 177: 283–301. 10.1007/BF01350721
Fan K: A generalization of Tychonoff's fixed point theorem. Mathematische Annalen 1961, 142: 305–310. 10.1007/BF01353421
Yu J: Essential weak efficient solution in multiobjective optimization problems. Journal of Mathematical Analysis and Applications 1992,166(1):230–235. 10.1016/0022-247X(92)90338-E
Acknowledgments
This paper was supported by the National Natural Science Foundation of China (11061023, 11071108), the Natural Science Foundation of Jiangxi Province (2010GZS0145), and the Youth Foundation of Jiangxi Educational Committee (GJJ10086).
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wang, S., Li, Q. Existence and Stability of Solutions for Implicit Multivalued Vector Equilibrium Problems. Fixed Point Theory Appl 2011, 381218 (2011). https://doi.org/10.1155/2011/381218
Received:
Accepted:
Published:
DOI: https://doi.org/10.1155/2011/381218
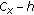 -pseudomonotone with respect to
-pseudomonotone with respect to 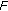 and
and 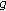 on
on  and
and 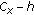 -pseudomonotone with respect to
-pseudomonotone with respect to 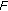 and
and  on
on 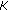 , respectively.
, respectively.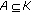 and
and  such that, for all
such that, for all 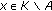 , one has
, one has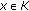 ,
,  .
.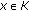 ,
, 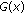 is convex.
is convex.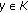 ,
, 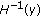 is compactly open.
is compactly open. has no fixed point in
has no fixed point in 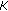 .
.